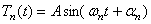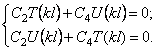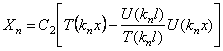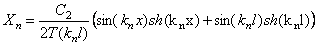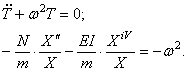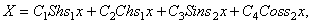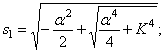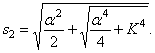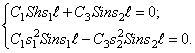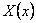МУ 4970: Определение моментов инерции тел методом крутильных колебаний
Лабораторная работа 1-20: Определение моментов инерции тел методом крутильных колебаний
Цель работы: изучение динамики вращательного движения твердых тел, знакомство с одним из методов определения моментов инерции тел – методом крутильных колебаний.
Приборы и принадлежности: унифилярный подвес ФПМ05, снабженный набором твердых тел (грузов) различной формы и электронным миллисекундомером.
Элементы теории
Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси имеет вид:
М – момент действующих на тело сил, взятый относительно оси вращения;
I – момент инерции тела относительно той же оси;
ϕ′′ – угловое ускорение тела.
Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы m точки и квадрата её расстояния r от оси:
Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных материальных точек (элементарных масс △mi ), на которые можно разбить тело:
В предельном случае, когда число элементарных масс стремится к бесконечности, сумма переходит в интеграл:
Как видно из определения, момент инерции тела есть величина аддитивная: момент инерции тела равен сумме моментов инерции его частей, а момент инерции системы равен сумме моментов инерции тел, входящих в систему.
Существуют различные способы экспериментального определения моментов инерции твердых тел. В данной работе используется метод вращательных (крутильных) колебаний.
Исследуемая система представляет собой твердое тело (например, брусок), подвешенное на струне, концы которой закреплены (рис. 1). После отклонения бруска на некоторый угол j от положения равновесия система начнет совершать крутильные колебания.
На основании формулы (1) уравнение движения бруска при малых углах отклонения ϕ примет вид:
I – момент инерции бруска относительно оси вращения;
r – коэффициент момента сил сопротивления;
k – коэффициент возвращающего (упругого) момента.
Коэффициент r численно равен моменту сил сопротивления при угловой скорости ϕ , равной 1 рад/с. А коэффициент k численно равен моменту упругих сил, возникающих при закручивании нити (струны) на угол, равный 1 рад.
Если сопротивление среды невелико, то первым членом правой части в уравнении (5) можно пренебречь и записать его в виде:
Обозначив kI = w 2 , окончательно получим дифференциальное уравнение гармонических колебаний:
Решение этого уравнения имеет вид:
ϕ0 – угловая амплитуда колебаний;
Как следует из приведенного решения (7), тело будет совершать гармонические колебания около положения равновесия. Циклическая частота w и период колебаний Т определяются величинами I и k по формулам:
Описание экспериментальной установки
Работа выполняется на установке – унифилярном подвесе ФПМ05, общий вид которого изображен на рис. 2.
Подвес представляет собой настольный прибор, на вертикальной стойке 1 которого размещены верхний и нижний кронштейны 2. Между кронштейнами 2 на стальной проволоке 3 подвешена рамка 4, предназначенная для установки и закрепления исследуемых тел 5, имеющих различные формы. В центрах граней грузов, в серединах их ребер и у вершин имеются углубления для закрепления в рамке.
На кронштейне 6 размещены: шкала 7, предназначенная для определения начального угла поворота рамки, электромагнит 8 для фиксации рамки в заданном положении и блок питания электромагнита 12. Электромагнит фиксируется в требуемом положении винтом 9.
На том же кронштейне 6 закреплен фотоэлектрический датчик 10. На основании 13 размещен миллисекундомер физический комбинированный 11, служащий для отсчета времени и числа колебаний.
В качестве исследуемых тел используются металлические грузы: цилиндр, параллелепипед и куб. Исследуемый груз закрепляется в рамке, начальное положение которой фиксируется электромагнитом. После отключения электромагнита (тумблер на блоке питания) рамка с грузом начинает совершать крутильные колебания.
Во время колебаний флажок, установленный на рамке, пересекает световой поток в щели фотоэлектрического датчика и сигнал, снимаемый с фотодиода, поступает на миллисекундомер.
Метод крутильных колебаний
Этот метод заключается в следующем. Тело с неизвестным моментом инерции I закрепляют в рамке подвеса. Период колебания такой системы будет равен
I0 – момент инерции ненагруженной рамки,
k – коэффициент упругости проволоки подвеса.
Согласно формуле (9) момент инерции I исследуемого тела можно вычислить, зная величины T, I0 и k. Период T колебаний несложно определить, измерив время t, за которое совершается N полных колебаний:
Для того, чтобы исключить неизвестные величины I0 и k, нужно измерить время t0 колебаний ненагруженной рамки, а также время tЭ колебаний рамки, нагруженной эталонным телом – телом с известным моментом инерции IЭ.
Таким образом, получаем систему уравнений:
Решая данную систему уравнений, получаем формулу для момента инерции выбранного нами тела:
Из выражения (12) следуют формулы для предельной относительной погрешности определяемого момента инерции:
△ t – погрешность измерения промежутка времени N полных колебаний рамки (предполагается, что эта погрешность одинакова для всех трех случаев измерения: t0, t и tэ).
Формулы (12) и (13) являются основными формулами для обработки результатов измерений, однако расчет существенно упрощается, если формулу (12) переписать в виде:
Если, кроме того, измеряемые промежутки времени t и tэразличаются незначительно, то малым по сравнению с единицей членом но пренебречь и представить (14) в виде:
Справедливость формулы (15) проверяется путем сравнения величины (t — tэ) (tэ+ t0 ) с относительной погрешностью результата EI, определяемой уравнением (13). Она справедлива, если:
Из уравнения (13) также следует, что чем больше полное время колебаний рамки, тем точнее получается результат. Поэтому в процессе прямых измерений рекомендуется измерять времена t0, t и tэдля
N = 50 колебаний рамки.
Задание
В задание входит определение моментов инерции двух тел различной формы относительно их центра масс теоретически и экспериментально.
Для теоретического расчёта моментов инерции по известным массам и размерам тел используются следующие выражения:
Iц и Iп — моменты инерции цилиндра и параллелепипеда соответственно;
R – радиус цилиндра;
a, b – размеры параллелепипеда.
Расчёт моментов инерции данных тел по экспериментально полученным данным производится по формулам (14) или (15). Необходимо также оценить абсолютные и относительные погрешности рассчитанных моментов инерции исследуемых грузов.
Порядок выполнения работы
Подготовка установки к работе
- Включите в сеть шнур питания миллисекундомера. Нажмите кнопку «СЕТЬ» на лицевой панели, при этом должны загореться цифровые индикаторы.
- После прогрева миллисекундомера (1–2 минуты) включите тумблер блока питания электромагнита.
- Ослабив стопорный винт электромагнита, установите его на угол, указанный преподавателем, в пределах 60-100º. Зафиксируйте электромагнит в этом положении тем же самым винтом.
- Поверните рамку так, чтобы металлический флажок, установленный на рамке, коснулся якоря электромагнита. При этом флажок притянется к якорю и рамка займет фиксированное положение.
- С помощью кнопок «СТОП» и «СБРОС» миллисекундомера обнулите счетчики числа и времени колебаний. Прибор готов к работе.
Проведение измерений
- Выключите тумблер блока питания электромагнита, при этом рамка начнет совершать колебательное движение и запустятся счетчики миллисекундомера. После N–1 полных колебаний рамки нажмите кнопку «СТОП» – отсчетное устройство, доработав до конца 50-го колебания, остановит счетчики. Запишите время t0– время 50-ти колебаний ненагруженной рамки. Число полных колебаний рамки может быть задано преподавателем дополнительно в пределах 30-60.
Остановив рукой колеблющуюся рамку, повторите операции, описанные в пп. 1.4, 1.5 и 2.1, еще два раза. Результаты измерений занесите в заранее подготовленную таблицу.
- Для закрепления исследуемого тела в рамке остановите рамку и освободите подвижную планку, отвернув гайки боковых цанг.
- Поднимите планку по направляющим и, придерживая её рукой, установите груз так, чтобы соответствующее углубление в центре одной из граней вошло в выступ на нижней перекладине рамки.
- Опустите подвижную планку по направляющим, затяните гайки боковых цанг и подожмите исследуемое тело винтом, находящимся на подвижной планке.
- Включите электромагнит и повторите операции, описанные в пп. 1.4, 1.5 и 2.1, три раза, результаты измерений занесите в таблицу.
- Для замены груза остановите рамку, отпустите гайки боковых цанг, переместите подвижную планку вверх и замените первый груз на второй, закрепив его в рамке, как указано в п. 2.4.
- Измерьте время 50-ти полных колебаний второго груза и эта- лонного тела по методике, описанной выше. В качестве эталонного тела можно использовать куб или цилиндр по указанию преподавателя. Результаты измерений занесите в таблицу.
- Измерьте размеры исследуемых тел простейшим измерительным прибором (штангенциркулем) и запишите эти значения, а также массу грузов в отчёт о лабораторной работе.
Порядок расчёта
- По выражениям (17), определяющим моменты инерции данных тел через массу и размеры, рассчитайте момент инерции эталонного тела (цилиндра или куба по указанию преподавателя). Оцените абсолютную погрешность по формулам:
R – радиус цилиндра;
a – сторона куба;
Jэц и Jэк моменты инерции цилиндра и куба, рассчитанные по выражениям (17);
△R и △a – систематическая погрешность измерений радиуса цилиндра и стороны куба соответственно.
- Рассчитайте относительную погрешность момента инерции эталонного тела.
- Используя данные таблицы, вычислите абсолютную и относительную погрешности измеренных промежутков времени t0 , t1 , t2 .
- По средним значениям промежутков времени N полных колебаний рамки с исследуемыми телами и без оцените относительные погрешности моментов инерции исследуемых тел по выражению (13).
Сравните последние с величиной |t — tэ| / (tэ+ t0 ) . Если неравенство (16) выполняется, то расчёт моментов инерции исследуемых грузов можно производить, применяя упрощённую формулу (15). В противном случае нужно использовать более точное выражение (14). Рассчитайте по соответствующим формулам моменты инерции исследуемых тел, а также абсолютные погрешности этих моментов инерции.
- По выражениям (17) вычислите теоретические моменты инерции исследуемых тел через массу и размеры. Оцените абсолютные по- грешности полученных значений моментов инерции по формулам (18) и (19), а также относительные погрешности.
- Сравните экспериментально полученные значения моментов инерции исследуемых тел с результатами расчётов по теоретическим формулам и сделайте соответствующие выводы.
Вопросы и задания для самоконтроля
- Сформулируйте основной закон динамики вращательного движения твердого тела.
- Дайте определение момента инерции твердого тела. Как его рассчитать теоретически?
- Получите дифференциальное уравнение крутильных колебаний, прокомментируйте его.
- Запишите уравнение колебательного движения крутильных колебаний. Чем определяется их период?
- Каковы прямые измерения в данной работе? В чем состоит роль эталонного тела?
Используя формулу (4), покажите, что моменты инерции цилиндра и прямоугольного параллелепипеда (рис. 3) относительно вертикальной оси их симметрии, проходящей через центр их масс, определяются выражениями (17).
Библиографический список
- Савельев И.В. Курс физики: учебник. 4-е изд. т. 1: Механика. Молекулярная физика. М.: Лань, 2008. 354 с.
- Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие для вузов. 8-е изд. М.: Академия, 2009. 720 с.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. 18-е изд. М.: Академия, 2010. 560 с.
Определение моментов инерции тел методом крутильных колебаний: методические указания к лабораторной работе / Рязан. гос. радио- техн. ун-т; cост.: М.А. Буробин, А.В. Брыков, Ю.В. Черкасова. Рязань, 2016. 8 с.
Представлена краткая теория крутильных колебаний, описан метод унифилярного подвеса. Приводятся порядок выполнения работы, методические указания по расчету погрешностей, контрольные вопросы и список рекомендуемой литературы.
Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 3. Библиогр.: 3 назв.
Вращательное движение твердого тела, момент инерции, крутильные колебания
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Определение моментов инерции тел методом крутильных колебаний Составители: Буробин Михаил Анатольевич
Брыков Александр Валериевич Черкасова Юлия Вадимовна
Редактор М.Е. Цветкова Корректор С.В. Макушина
Подписано в печать 15.02.16. Формат бумаги 60×84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
Раздел 6. Свободные колебания систем с распределёнными параметрами
Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.
6.1. Продольные колебания стержней
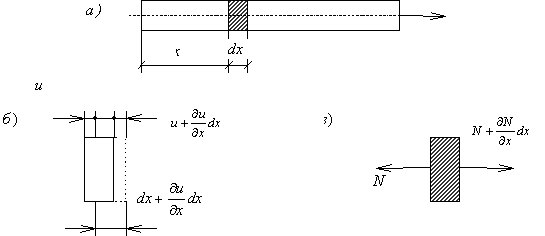
При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.
Пусть u — продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x ) и от времени t . Таким образом, 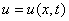
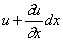
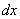
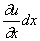
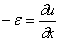
Соответственно продольная сила в сечении с координатой х может быть записана в виде
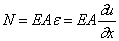
где 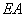
Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила 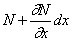
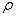
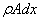
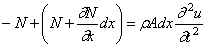
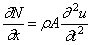
Учитывая (173) и принимая A = const , получим
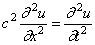
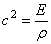
Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде
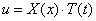
т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х , а другая только от аргумента t . Тогда вместо определения функции двух переменных u ( x , t ) необходимо определять две функции X( x ) и T( t ), каждая из которых зависит только от одной переменной.
Подставив (177) в (174), получим
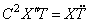
где штрихами обозначена операция дифференцирования по x , а точками – по t . Перепишем это уравнение таким образом:
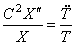
Здесь левая часть зависит только от x,а правая – только от t . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через 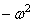
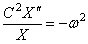
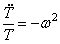
Отсюда следуют два уравнения:
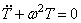
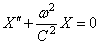
Первое уравнение имеет решение:
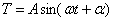
указывающее на колебательный характер, причём из (180) видно, что неизвестная величина 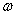
Второе из уравнений (179) имеет решение:
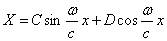
определяющее форму колебаний.
Частотное уравнение, определяющее величину 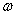
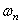
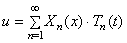
Функции Xn ( x ) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид
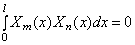
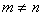
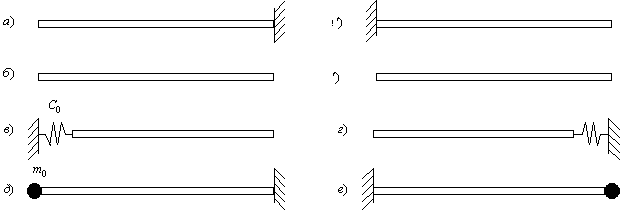
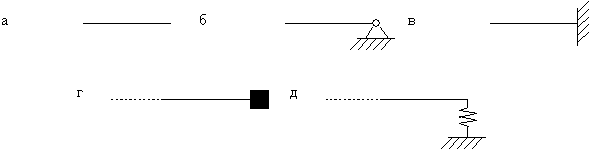
Рассмотрим некоторые варианты граничных условий.
Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении
Свободный конец стержня (рис.68,б). В концевом сечении продольная сила
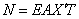
должна тождественно равняться нулю, что возможно, если в концевом сечении X’=0.
Упругозакреплённый конец стержня (рис.68,в).
При перемещении u концевого стержня возникает упругая реакция опоры 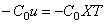
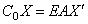
если опора расположена на левом конце стержня (рис.68,в), и
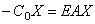
если опора расположена на правом конце стержня (рис.68,г).
Сосредоточенная масса 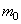
Развиваемая массой сила инерции:
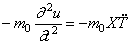
Так как, согласно первому из уравнений (179), 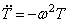
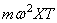
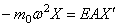
если масса находится на левом конце (рис.68,д), и
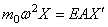
если масса связана с правым концом (рис.68,е).
Определим собственные частоты консольного стержня (рис.68,a’).
Согласно (182) и (183), граничные условия
X’=0 при х= 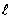
Подставляя поочерёдно эти условия в решение (181), получим
D=0; 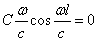
Условие С 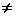
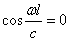
Корни этого уравнения
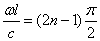
определяют собственные частоты:
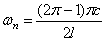
Первая (низшая) частота при n=1:
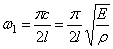
Вторая частота (при n=2):
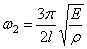
Определим собственные частоты стержня с массой 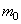
Согласно (182) и (184), имеем
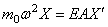

Подставляя эти условия в решение (181), получим:
D=0; 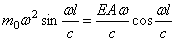
Следовательно, частотное уравнение при учёте (176) имеет вид
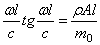
Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.
Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.
При 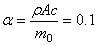
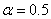
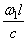
При малом отношении 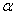
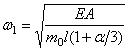
Для стержней переменного сечения, т.е. при А 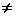
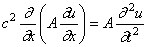
Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.
6.2. Крутильные колебания валов
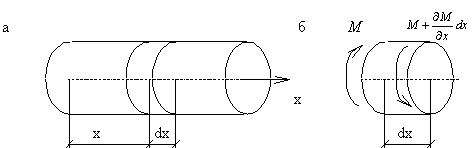
Крутильные колебания вала с непрерывно распределенной массой (рис.69,а) описываются уравнениями, которые по структуре полностью совпадают с приведенными выше уравнениями продольных колебаний стержней.
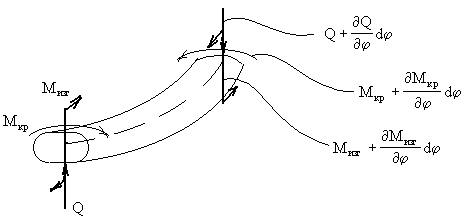
Крутящий момент М в сечении с абсциссой х связан с углом поворота 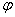
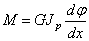
где Jp-полярный момент инерции поперечного сечения.
В сечении, расположенном на расстоянии dx , крутящий момент равен (рис.69,б):
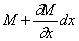
Обозначая через 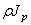
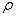
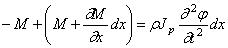
или подобно (174):

Подставляя сюда выражение (186), при Jp=const получим, аналогично (175):
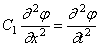
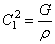
Общее решение уравнения (187), как и уравнения (175), имеет вид
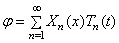
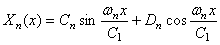
Собственные частоты и собственные функции при этом определяются конкретными граничными условиями.
В основных случаях закрепления концов аналогично случаю продольных колебаний получим
а) закрепленный конец ( 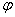
б) свободный конец (М=0): Х’=0;
в) упругозакрепленный левый конец: СоХ=GJpX ‘ ( Со-коэффициент жёсткости);
г) упругозакрепленный правый конец: — СоХ=GJpX ‘;
д ) диск на левом конце: 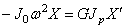
е) диск на правом конце: 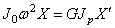
Если вал закреплён на левом конце (х=0), а правый конец ( х= 

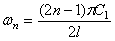
Если левый конец закреплён, а на правом конце имеется диск, получим трансцендентное уравнение:
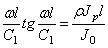
Если оба конца вала закреплены, то граничные условия будут X=0 при х=0 и х= 
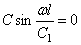
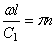
отсюда находим собственные частоты:
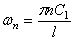
Если левый конец вала свободен, а на правом конце имеется диск, то X’=0 при х=0 ; Jo 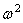

При помощи (188) находим
С=0; 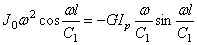
или трансцендентное частотное уравнение:
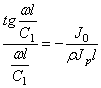
6.3.Изгибные колебания балок
6.3.1.Основное уравнение
Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:
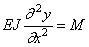
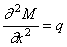
где EJ — жёсткость при изгибе; y=y ( x , t ) — прогиб; M=M( x , t ) — изгибающий момент; q — интенсивность распределённой нагрузки.
Объединяя (189) и (190), получим
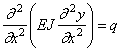
В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:
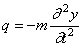
где m — интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид
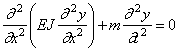
В частном случае постоянного поперечного сечения, когда EJ = const , m = const , имеем:
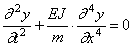
Для решения уравнения (192) полагаем, как и выше,
y = X ( x ) × T ( t ). (193)
Подставляя (193) в (192), приходим к уравнению:
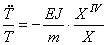
Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через 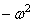
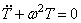
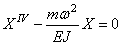
Первое уравнение указывает на то, что движение носит колебательный характер с частотой 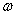
Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид
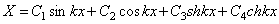
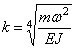
Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:
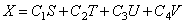

представляют собой функции А.Н.Крылова.
Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:
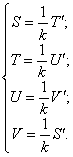
Поэтому производные выражения (197) записываются в виде
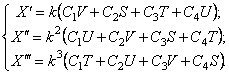
В задачах рассматриваемого класса число собственных частот 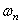
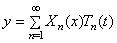
Для определения собственных частот и формул необходимо рассмотреть граничные условия.
6.3.2. Граничные условия
Для каждого конца стержня можно указать два граничных условия .
Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX»’T и изгибающий момент M=EJX»T. Поэтому граничные условия имеют вид
Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX»T. Следовательно, граничные условия таковы:
Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота 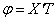
На конце стержня имеется точечный груз массы 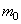
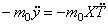
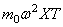
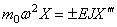
В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .
Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX»’T равна реакции опоры 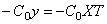
X»=0 ; 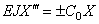
(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).
6.3.3. Частотное уравнение и собственные формы
Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C1, C2, C3, C4.
Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C1, C2, C3, C4, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).
Проследим составление частотных уравнений на примерах.
Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X»=0 при x=0 и x= 
Чтобы C2 и C4 не были равны нулю, необходимо равенство нулю определителя:
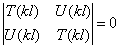
Таким образом, частотное уравнение имеет вид
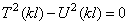
Подставляя выражения T и U, получим
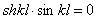
Так как 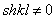
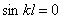
Корни этого уравнения:
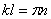
Учитывая (196), получим
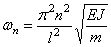
Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C2 и C4:
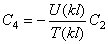
Следовательно, (197) приобретает вид
Согласно (207), имеем
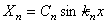
где 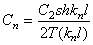
6.3.4. Определение движения по начальным условиям
Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:

и использовать свойство ортогональности собственных форм:
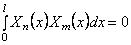
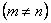
Общее решение (201) запишем так:
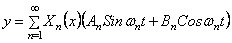
Скорость определяется выражением

Подставляя в правые части уравнений (211) и (212) 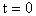
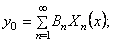
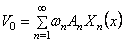
Умножая эти выражения на 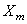
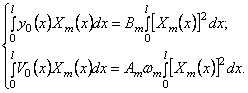
Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных 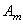
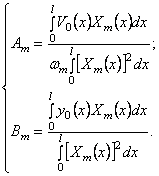
Теперь эти результаты нужно подставить в решение (211).
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо 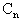
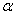
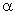
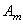
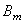
6.3.5. Влияние постоянной продольной силы
Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N , величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)
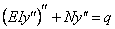
Полагая 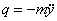
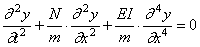
Принимаем по-прежнему частное решение в виде 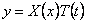
Тогда уравнение (215) распадается на два уравнения:
Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:

где K определяется формулой (196), а
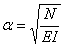
Решение уравнения (216) имеет вид
Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце 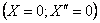
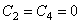
Приравнивая нулю определитель, составленный из коэффициентов при величинах 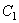
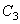
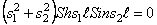
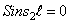
Корни этого частотного уравнения:
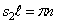
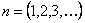
Следовательно, собственная частота определится из уравнения
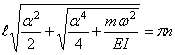
Отсюда при учёте (217) находим
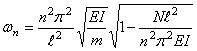
При растяжении 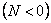
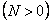
6.3.6. Влияние цепных усилий
Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.
Если в мгновение t прогибы балки определяются функцией 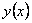
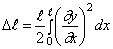
Соответствующее цепное усилие найдём при помощи закона Гука
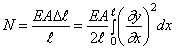
Подставим этот результат в (215) вместо продольной силы N (с учётом знака)
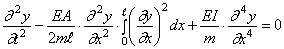
Полученное нелинейное интегродифференциальное уравнение упрощается при помощи подстановки
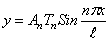
где 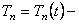
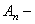
Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение
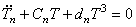
коэффициенты которого имеют следующие значения:
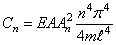
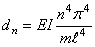
Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.
Точное решение для 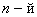
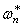
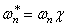
где 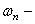
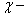
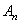
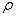
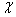
При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то 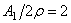
Случай 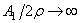
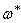
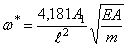
Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.
При этом формула для частоты имеет вид
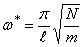
где N — постоянная растягивающая сила.
6.4. Влияние вязкого трения
Ранее предполагалось, что материал стержней идеально упругий и трение отсутствует. Рассмотрим влияние внутреннего трения, считая, что оно является вязким; тогда связь напряжений с деформациями описывается соотношениями
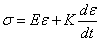
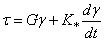
Пусть стержень с распределёнными параметрами совершает свободные продольные колебания. В этом случае продольная сила запишется в виде
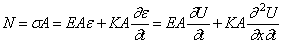
Из уравнения движения элемента стержня было получено соотношение (174)
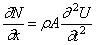
Подставляя сюда (224), приходим к основному дифференциальному уравнению
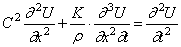
которое отличается от (175) вторым слагаемым, выражающим влияние сил вязкого трения.
Следуя методу Фурье, ищем решение уравнения (225) в виде
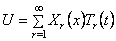
где 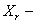
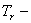
При этом каждый член ряда должен удовлетворять граничным условиям задачи, а вся сумма — также и начальным условиям. Подставляя (226) в (225) и требуя, чтобы равенство удовлетворялось для любого номера r , получим
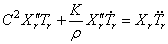
где штрихи обозначают дифференцирование по координате x , а точки — дифференцирование по времени t .
Разделив (227) на произведение 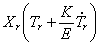
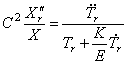
левая часть, которого может зависеть только от координаты x , а правая — только от времени t . Для тождественного выполнения равенства (228) необходимо, чтобы обе части были равны одной и той же постоянной, которую обозначим через 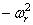
Из этого следуют уравнения
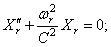
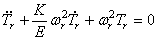
Уравнение (229) не зависит от коэффициента вязкости K и, в частности, остаётся таким же в случае идеально упругой системы, когда 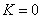
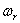
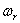
Теперь перейдём к уравнению (230), описывающему процесс затухающих колебаний; его решение имеет вид
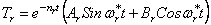
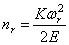
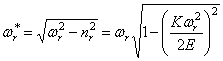
Выражение (232) определяет темп затухания, а (233) — частоту колебаний.
Таким образом, полное решение уравнения задачи
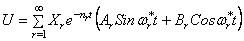
Постоянные 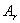

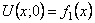
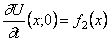
где 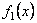
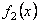
Тогда при 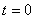
умножая обе части этих равенств на 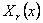

Соответственно условию ортогональности собственных форм все остальные слагаемые, входящие в правые части этих равенств, обращаются в нуль. Теперь из равенств (236) легко найти 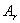

Рассматривая (232) и (234), заметим, что чем выше номер формы колебаний 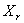
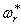
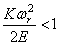
При достаточно больших значениях r неравенство (237) нарушается и величина 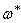
Все эти качественные выводы относятся не только к случаю продольных колебаний, но и к случаям крутильных и изгибных колебаний.
6.5. Колебания стержней переменного сечения
В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения
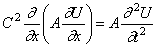
Уравнение крутильных колебаний (187) должно быть заменено уравнением
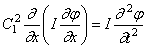
а уравнение поперечных колебаний (192) – уравнением
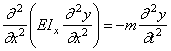
Уравнения (238)-(240) при помощи однотипных подстановок 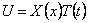
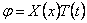
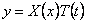
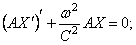
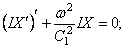
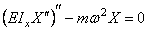
и одному однотипному уравнению для функции 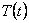
Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.
Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные 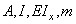
6.6. Колебания круговых колец
6.6.1. Колебания в плоскости кольца
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой 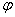
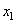
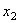
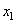
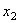
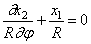
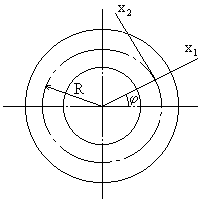
Угол поворота поперечного сечения бруса в процессе движения определяется формулой
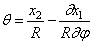
Изменение кривизны бруса 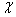
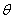
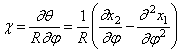
Изгибающий момент в поперечном сечении кольца:
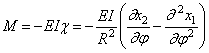
Теперь составим уравнение движения элемента 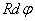
Помимо перечисленных сил, на элемент действует также сила инерции:
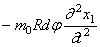
где 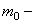
Проектируя приложенные к элементу силы на радиус, получим
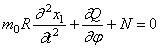
Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:
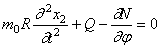
Уравнение моментов имеет вид
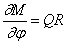
Исключим из (248) и (249) нормальную силу N , а поперечную силу Q заменим её значением из (250):
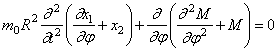
Подставляя сюда значение M из (247), получим уравнение движения в перемещениях 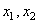
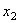
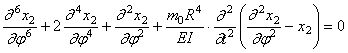
Решение уравнения движения (252) будем искать в виде
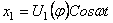
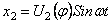
При этом для 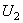
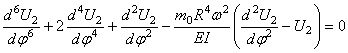
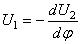
Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям. На каждом конце бруса должны быть равны нулю либо компоненты перемещений 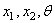
Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять
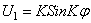
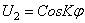
Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если
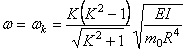
Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению 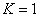
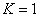
6.6.2. Колебания, перпендикулярные плоскости кольца
В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением 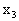
Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х3, а затем — с х4.
Если х3 постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х3 изменяется в зависимости от центрального угла по линейному закону 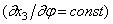
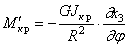
где GJ кр — крутильная жёсткость бруса.
Если при этом отлична от нуля и вторая производная 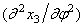
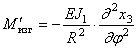
где J 1 — момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.
Найдём силовые факторы, связанные с поворотом х4. Если х4 постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент
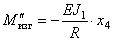
При переменном по длине повороте х4 соседние сечения поворачиваются друг относительно друга и возникает крутящий момент
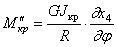
Суммируя силовые факторы, связанные с перемещениями х3 и х4, ,получаем
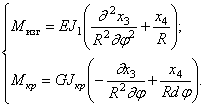
Составим уравнение движения элемента Rd 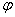
Будем пренебрегать инерцией поворота элемента вокруг своей оси.
Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:
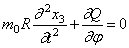
Сумма моментов относительно нормали к оси элемента:
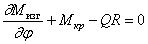
Сумма моментов относительно касательной к оси элемента:
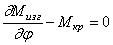
Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х3 и х4:
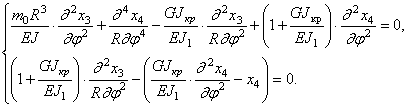
Ограничиваясь исследованием собственных колебаний замкнутого кольца, решение уравнений (260) можно представить в виде
x3 = Acosk j × cos w t , x4 = Bcosk j × cos w t . (261)
Подставляя значения (261) в уравнение движения (260), получим
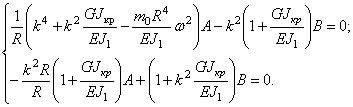
Из равенства нулю определителя этой системы получим частотное уравнение, корни которого — собственные частоты — таковы:
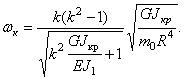
Наименьшая отличная от нуля частота соответствует k =2.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Определение момента инерции тела методом крутильных колебаний
Основными характеристиками динамики вращательного движения являются: момент инерции и момент силы.
Момент инерции– есть мера инертности тела, имеющего ось вращения.
Во вращательном движении момент инерции имеет такую же роль, как масса при поступательном движении. Как и масса момент инерции (относительно оси вращения) скалярная величина. Однако величина момента инерции тела зависит от положения оси вращения.
Момент инерции материальной точки относительно оси вращения, находящейся на расстоянии r, равен произведению массы на квадрат расстояния до оси вращения 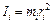
Момент инерции твердого тела равен сумме моментов инерции его составных точек 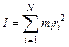
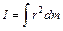
Момент инерции относительно произвольной оси, не проходящей через центр масс, можно вычислить по теореме Штейнера.
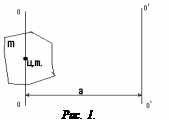
Момент силы – величина векторная, численно равная произведению силы на плечо
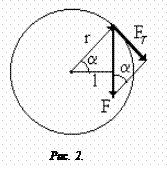
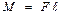
Плечом называется кратчайшее расстояние от оси вращения до линии действия силы (рис.2).
Момент силы и момент инерции связаны соотношением:
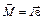
где ε – угловое ускорение.
Это есть основное уравнение динамики для вращательного движения.
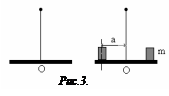
Применим к этим колебаниям основное уравнение вращательного движения. При крутильных колебаниях на тело действует возвращающий момент со стороны нити подвеса, обусловленный упругими силами.
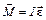
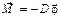

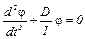
Полученное уравнение является дифференциальным уравнением крутильных колебаний, в этом уравнении отношение D/I = w 2 – циклическая частота – ω.
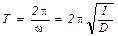
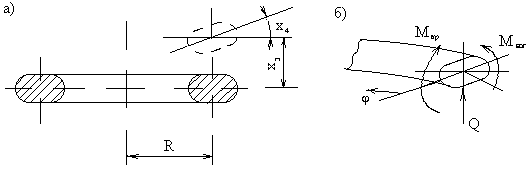
Вывод рабочей формулы.Воспользуемся методом крутильных колебаний для определения момента инерции диска, подвешенного на упругой нити (рис.4).
Для этого используем формулу периода крутильных колебаний. Однако в этой формуле две неизвестные величины: I – момент инерции диска относительно оси О, проходящей через центр масс диска, и D – модуль упругости нити.
Учитывая аддитивные свойства момента инерции, поставим на диск два груза и запишем второе уравнение
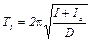
где Ia – момент инерции двух грузов относительно оси О. Возведем (5,6) в квадрат и разделим одно уравнение на другое:
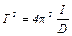

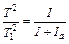
Выразим момент инерции диска
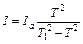
Момент инерции двух грузов относительно оси О по теореме Штейнера равен:
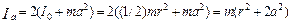
где I0 – момент инерции цилиндра относительно его оси, проходящей через центр масс. Подставим полученное выражение в предыдущую формулу и получим:
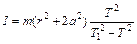
где r – радиус цилиндра, a – расстояние между осями диска и цилиндра.
Выражение (7) является рабочей формулой для расчета момента инерции диска.
Дата добавления: 2015-10-05 ; просмотров: 1659 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://www.detalmach.ru/lectdinamika6.htm
http://helpiks.org/5-56994.html