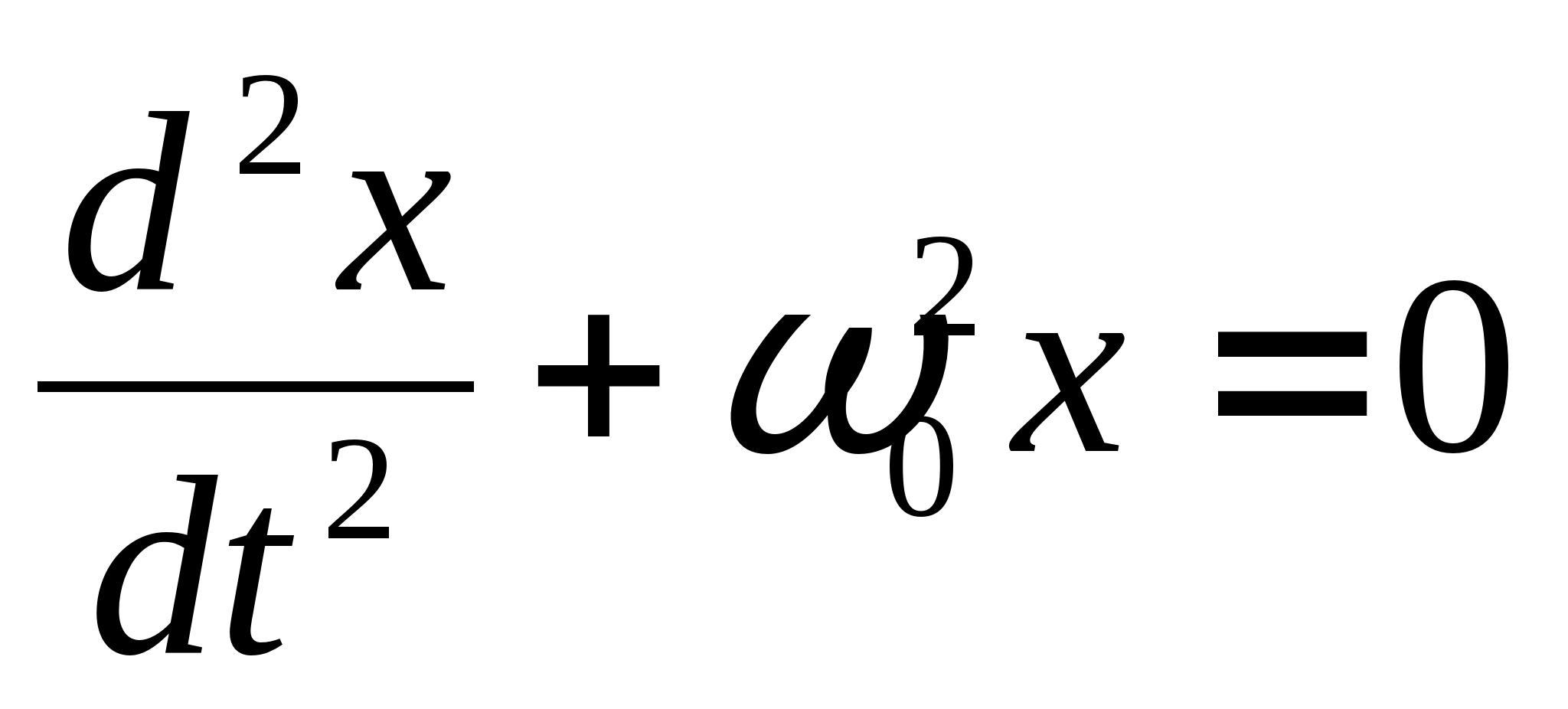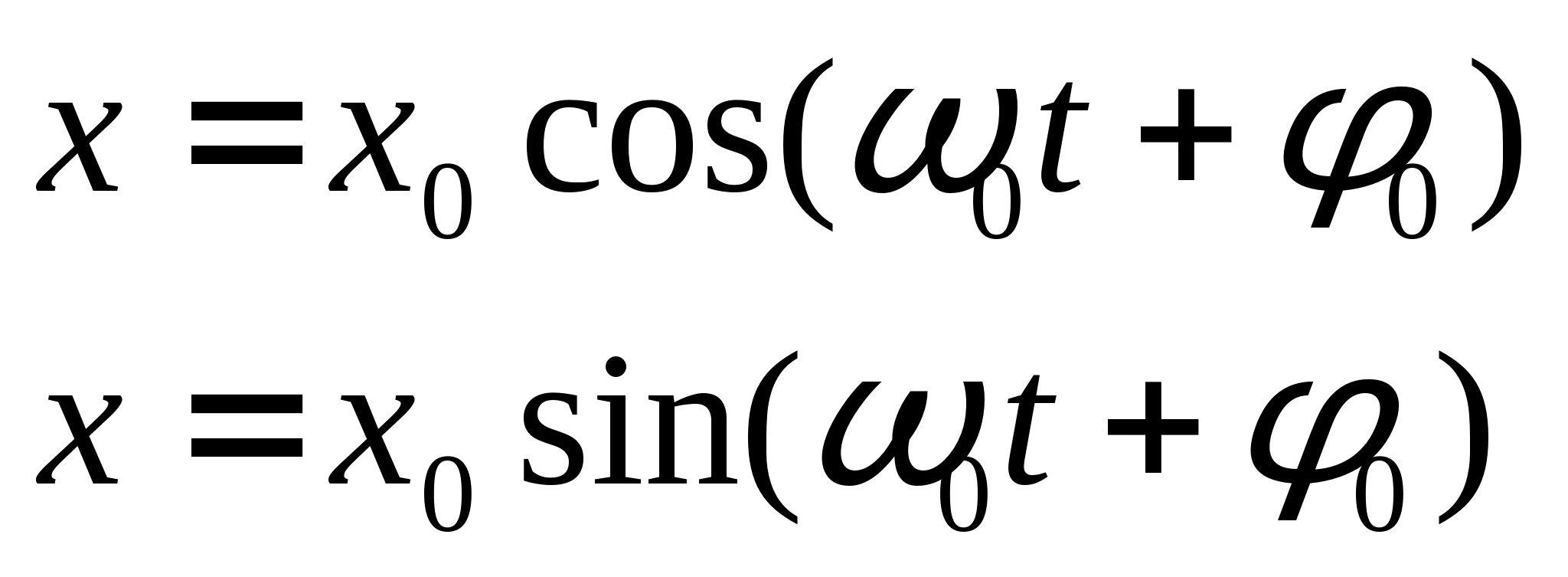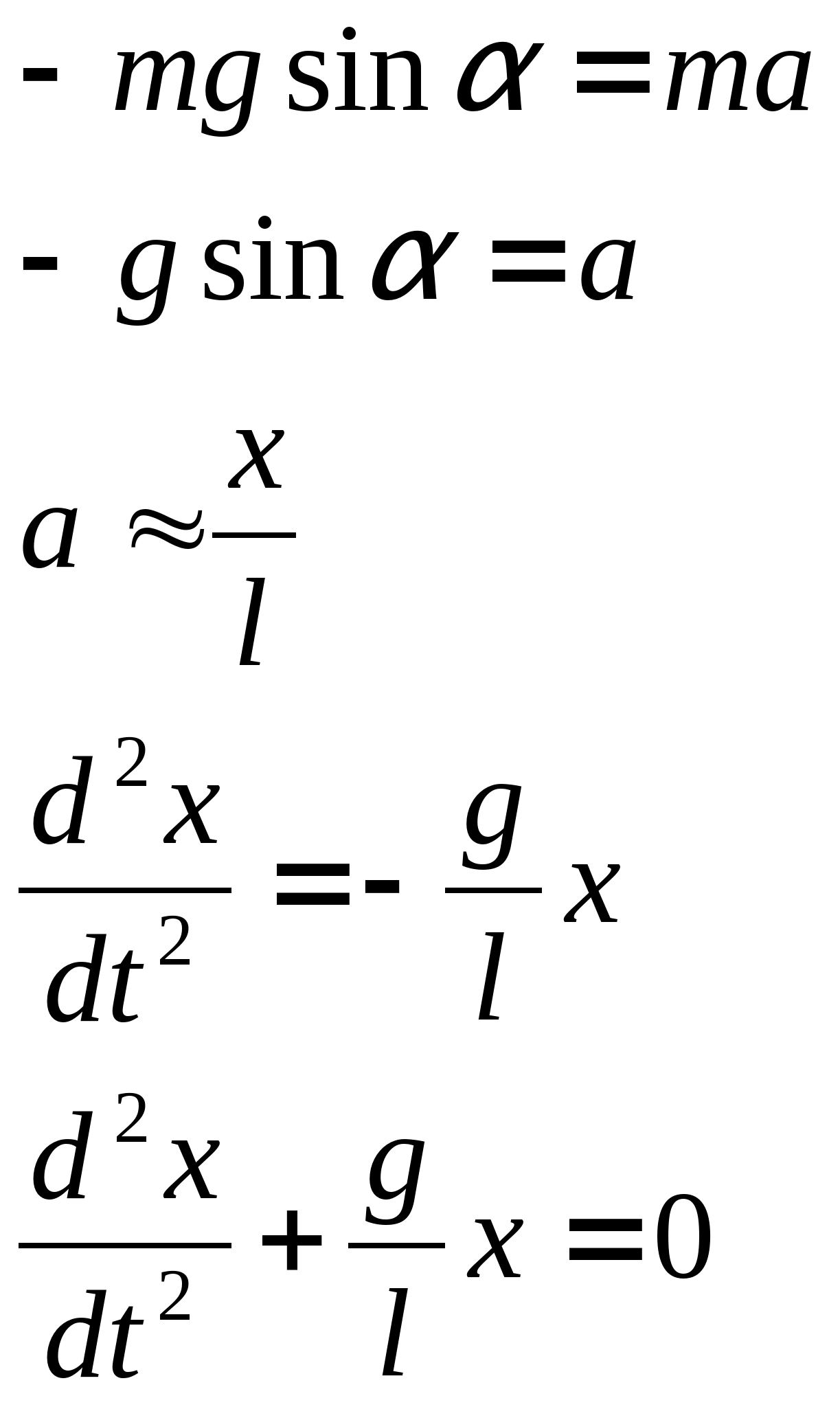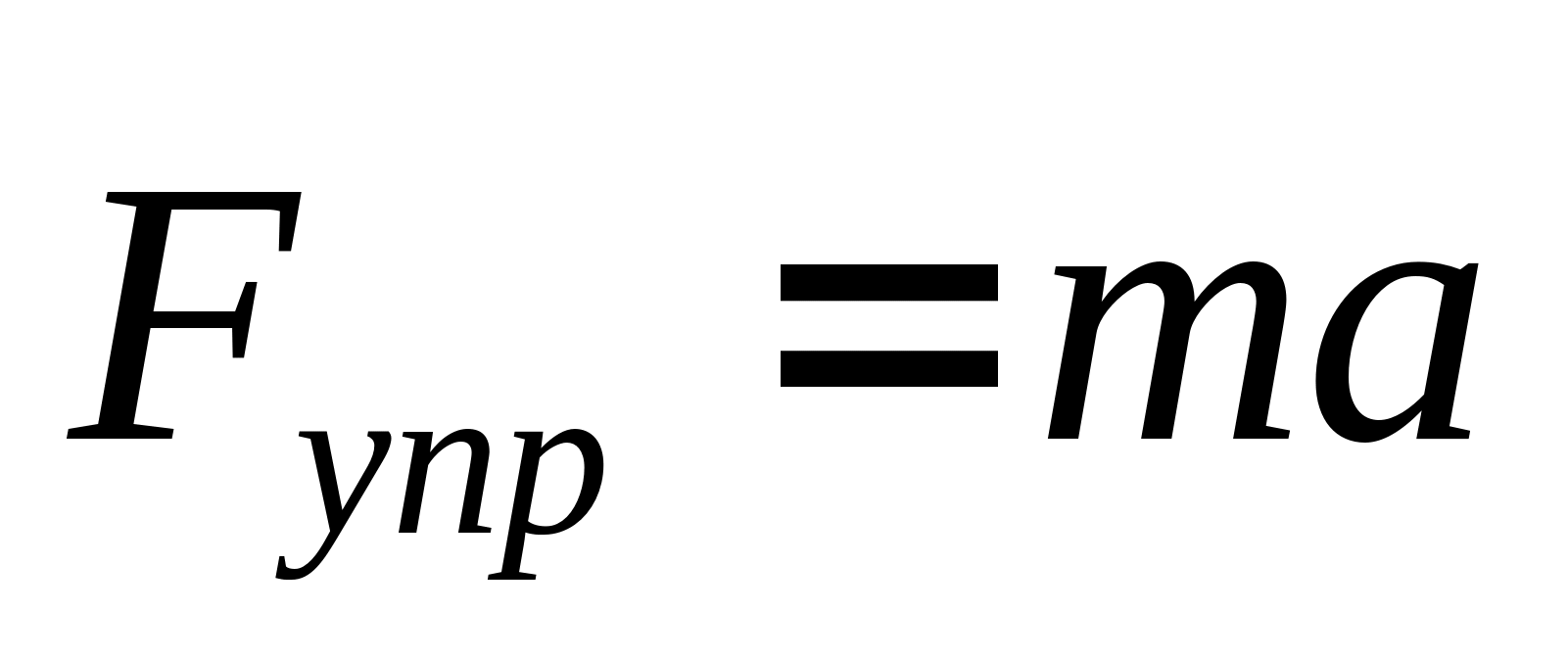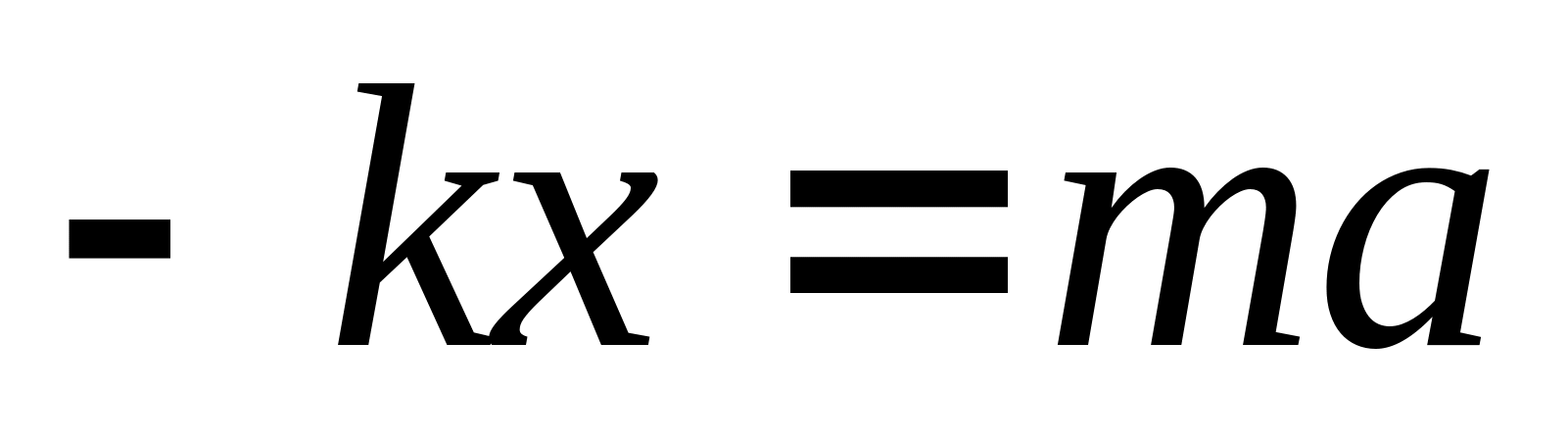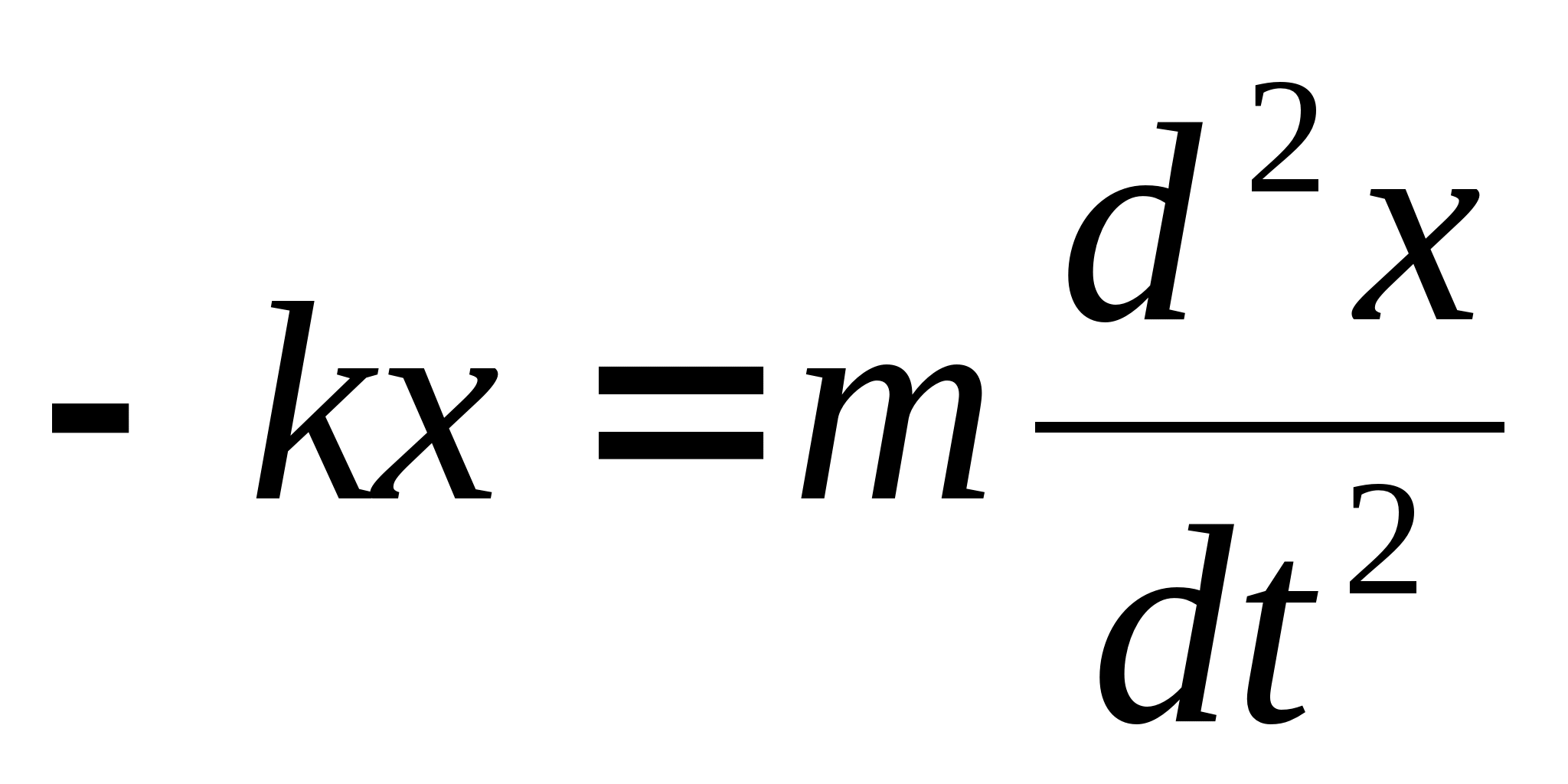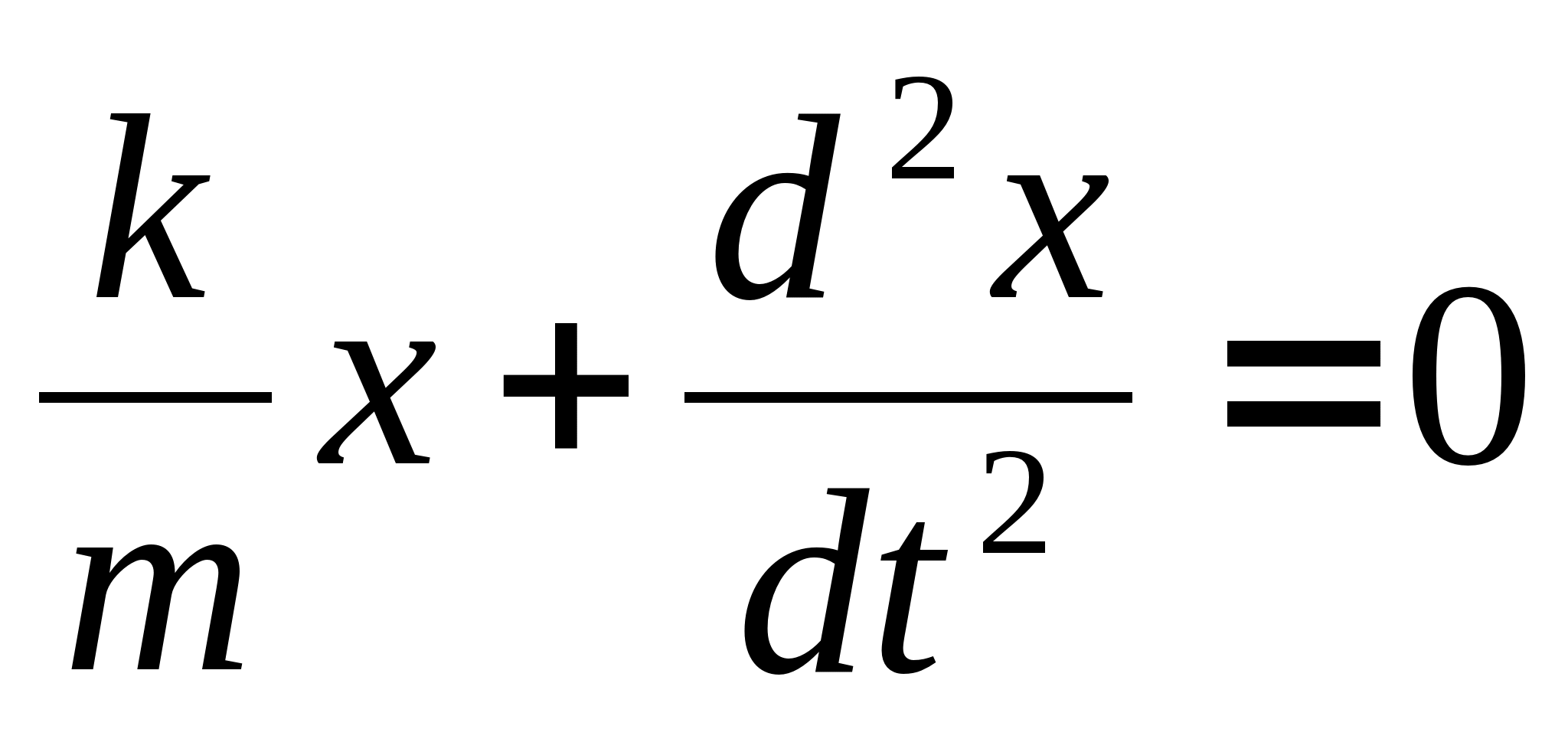Уравнение свободных незатухающих гармонических колебаний.
Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t=0 (рис. 19, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 19, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 19, в). Далее те же процессы начнут протекать в обратном направлении (рис. 19, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 19, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения UC на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение UC на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть :
.
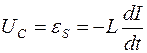
Исходя из того, что UC=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
или 
.
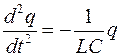
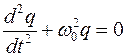
Решением этого дифференциального уравнения является функция q(t), то естьуравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
,
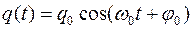
где q(t) – величина заряда на обкладках конденсатора в момент времени t;
q0 – амплитуда колебаний заряда на обкладках конденсатора;
– круговая (или циклическая) частота колебаний ( 
) ;
=2 
/T (T – период колебаний, 
–формула Томсона);
– фаза колебаний в момент времени t;
– начальная фаза колебаний, то есть фаза колебаний в момент времени t=0.
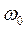
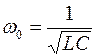
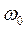
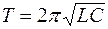
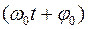
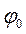
Уравнение свободных затухающих гармонических колебаний.В реальном колебательном контуре учитывается, что кроме катушки индуктивностью L, конденсатора емкостью С, в цепи также имеется резистор сопротивлением R,отличным от нуля, что является причиной затухания колебаний в реальном колебательном контуре. Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Для цепи реального колебательного контура напряжения на последовательно включенных конденсаторе емкостью С и резисторе сопротивлением R складываются. Тогда с учетом закона Фарадея для цепи реального колебательного контура можно записать:
,
где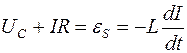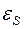 
– электродвижущая сила самоиндукции в катушке;
IR – напряжения на резисторе.
Исходя из того, что I=dq/dt, получаем дифференциальное уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
или 
,
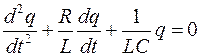
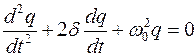
где 
– коэффициент затухания колебаний ( 
) , 
.
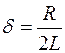
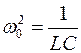
Решением полученного дифференциального уравнения является функция q(t), то естьуравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
,
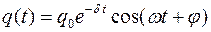
где q(t) – величина заряда на обкладках конденсатора в момент времени t;
– амплитуда затухающих колебаний заряда в момент времени t ;
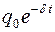
q0 – начальная амплитуда затухающих колебаний заряда;
– круговая (или циклическая) частота колебаний ( 
);
– фаза затухающих колебаний в момент времени t;
– начальная фаза затухающих колебаний.
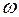
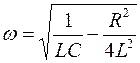
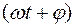
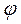
Период свободных затухающих колебаний в реальном колебательном контуре :
.
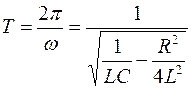
Вынужденные электромагнитные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо в процессе колебаний компенсировать потери энергии. Такая компенсация в реальном колебательном контуре возможна с помощью внешнего периодически изменяющегося по гармоническому закону переменного напряжения U(t):
.
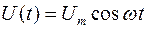
В этом случае дифференциальное уравнение вынужденных электромагнитных колебанийпримет вид:
или 
.
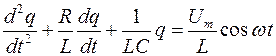
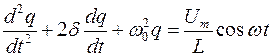
Решением полученного дифференциального уравнения является функция q(t):
.
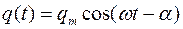
В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими, а амплитуда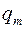 
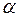
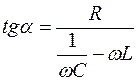
и фаза колебаний 
определяются следующими выражениями:
; 
.
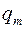
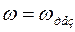
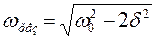
Отсюда следует, что амплитуда колебаний величины заряда имеет максимум при резонансной частоте внешнего источника 
:
.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающего переменного напряжения к частоте, близкой частоте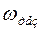 
, называется резонансом.
Тема 10. Электромагнитные волны
Согласно теории Максвелла электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость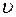 
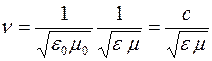
распространения которых определяется выражением:
,
где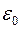 
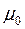
и 
– соответственно электрическая и магнитная постоянные,
e и m – соответственно электрическая и магнитная проницаемости среды,
с – скорость света в вакууме (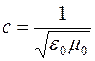 
) .
В вакууме (e = 1, m = l) скорость распространения электромагнитных волн совпадает со скоростью света( с ), что согласуется с теорией Максвелла о том,
что свет представляет собой электромагнитные волны.
По теории Максвелла электромагнитные волны являются поперечными,то есть векторы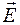 
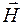
и 
напряженностей электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 
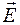
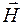
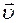
скорости распространения волны, причем векторы , и образуют правовинтовую систему (рис. 20).
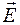
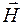
Из теории Максвелла следует также, что в электромагнитной волне векторы и колеблются в одинаковых фазах (рис. 20), то есть значения напряженностей Е и Н электрического и магнитного полей одновременно достигают максимума и одновременно обращаются в нуль, причем мгновенные значения Е и Н связаны соотношением: 
.
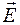
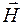
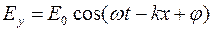
Уравнение плоской монохроматической электромагнитной волны (индексы у и z при Е и Н подчеркивают лишь то, что векторы и направлены вдоль взаимно перпендикулярных осей в соответствии с рис. 20):
,
,
где E0 и Н0– соответственно амплитуды напряженностей электрического и магнитного полей,
w – круговая частота волны,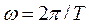 
(T – период колебаний),
k – волновое число,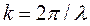 
( 
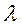
– длина волны),
j – начальная фаза колебаний (начальная фаза колебаний j имеет одинаковое значение как для колебания электрического, так и магнитного векторов, так как в электромагнитной волне эти колебания происходят в одинаковых фазах).
Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл электрического и wм магнитного полей:
.
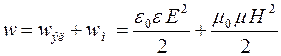
Учитывая выражение связи между величинами Е и Н , можно получить, что суммарная плотность энергии электрического и магнитного полей:
.
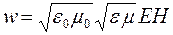
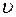
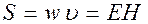
Умножив плотность энергии w на скорость распространения волны в среде, получим модуль плотности потока энергии:
.
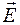
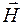
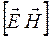
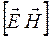
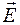
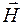
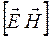
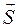
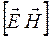
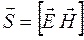
Tax как векторы и взаимно перпендикулярны, то произведение EH совпадает с модулем вектора 
( – векторное произведение векторов и ). Кроме того, направление вектора совпадает с направлением распространения волны, то есть с направлением переноса энергии, что позволило ввести вектор 
,равныйвекторному произведению , как вектор плотности потока электромагнитной энергии, называемыйвектором Умова–Пойнтинга:
.
Итак, вектор 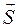направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Дифференциальное уравнение для свободных незатухающих колебаний имеет вид
1.Свободные механические и электрические колебания. Дифференциальное уравнение свободных колебаний и его решения.
Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
Дифференциальное уравнение свободных незатухающих колебаний:
Гармоническими называются колебания, происходящие по законам синуса или косинуса.
— амплитуда колебаний – максимальное смещение колеблющейся величины относительно положения равновесия.
— фаза колебаний. Показывает, какая часть колебаний завершена к данному моменту времени.
— начальная фаза колебаний.
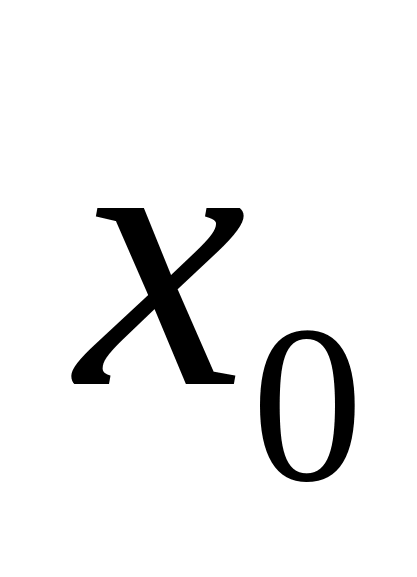
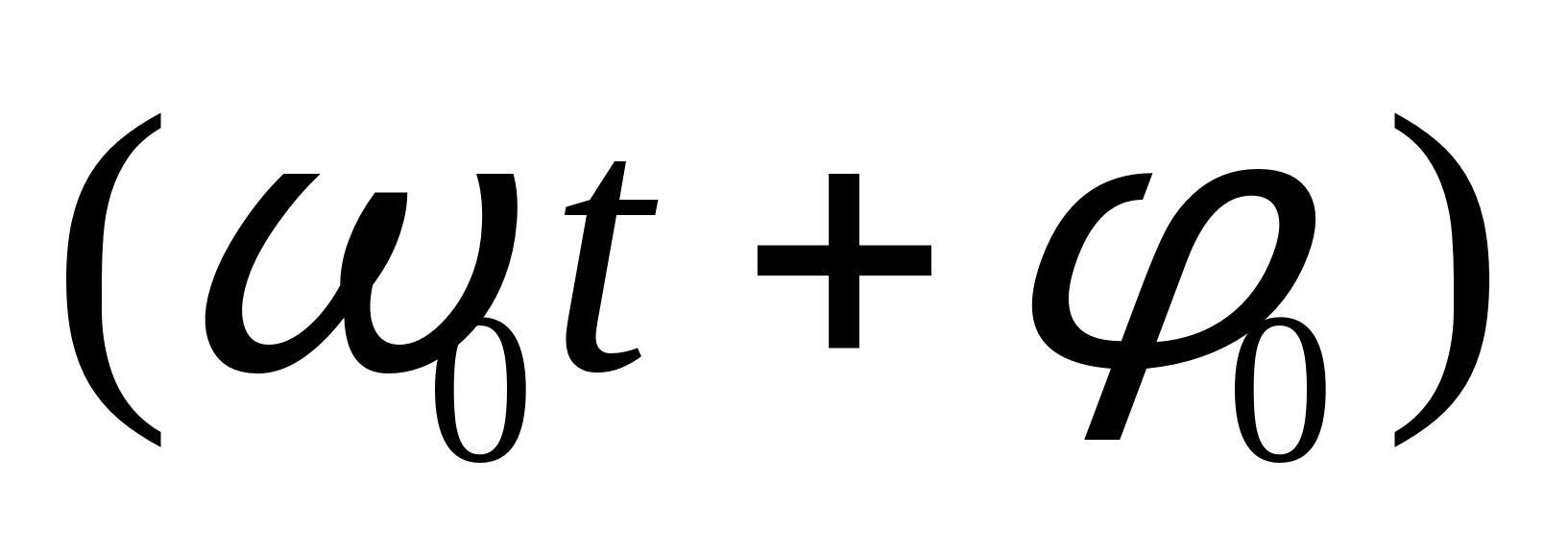
Математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити длины l.
Пружинный маятник — механическая система, состоящая из пружины жёсткостью k, один конец которой жёстко закреплён, а на втором находится груз массы m.
Свободные электромагнитные колебания:
(идеальная катушка)
Лекция № 5 Свободные электромагнитные колебания
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Выписка из рабочей программы дисциплины «Колебания и волны» – 010900
2.1 Свободные электромагнитные колебания.
Колебательный контур. Процессы в идеализированном колебательном контуре. Электромагнитные гармонические колебания. Дифференциальное уравнение свободных незатухающих электромагнитных колебаний и его решение. Собственная частота свободных электромагнитных колебаний. Формула Томсона. Закон сохранения и превращения энергии в идеализированном колебательном контуре.
1. Свободные электромагнитные колебания
Электромагнитные колебания представляют собой взаимосвязанные периодические изменения зарядов, токов, характеристик электрического и магнитного полей, сопровождающиеся взаимными превращениями этих полей.
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из конденсатора ёмкостью 
и катушки индуктивностью 
.
Если сопротивление контура 
равно нулю, колебательный контур называют идеальным. В идеальном колебательном контуре отсутствуют потери энергии, поэтому собственные колебания, возникающие в нем, являются незатухающими.
Рассмотрим процесс возникновения свободных незатухающих колебаний в идеальном колебательном контуре. Чтобы возбудить колебания, необходимо сообщить конденсатору некоторый заряд, а потом замкнуть ключ К (рис.1).
Пусть в начальный момент времени (
) конденсатору сообщили некоторый заряд 
. При этом напряжение между его обкладками 
, напряженность электрического поля 
и энергия электрического поля 
– максимальны, а ток в цепи отсутствует (рис. 2,а). Затем начинается разряд конденсатора. Возникающий при этом разрядный ток, проходя через катушку , создает в ней изменяющееся магнитное поле, которое продолжает расти до тех пор, пока ток не достигает максимального значения 
. При этом вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки 
, а индукция магнитного поля достигает максимума 
(рис. 2,б). Несмотря на то, что конденсатор полностью разрядился, ток в колебательном контуре не прекращается и поддерживается э. д.с. самоиндукции, что в итоге приведет к перезарядке конденсатора. При этом заряд конденсатора, напряжение между обкладками, напряженность и энергия электрического поля вновь достигают максимальных значений, однако полярность обкладок конденсатора и направление напряженности электрического поля между ними противоположны тем, какие были в начальный момент времени (рис. 2, в). По окончании перезарядки энергия магнитного поля катушки перейдет в энергию электрического поля конденсатора. Начиная с этого момента, ток в контуре меняет направление, и процесс воспроизводится в обратном направлении (рис. 2, г). Система возвращается в исходное состояние (рис. 2, д), и начинается следующий период колебаний.
В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора 
от времени 
, 
, на котором значениям заряда в моменты времени 
сопоставлены соответствующие состояния колебательного
контура (а; б; в; г; д).
Так как сопротивление контура равно нулю, т. е. нет потерь энергии, такой процесс должен продолжаться бесконечно, а возникающие колебания называются собственными или свободными.
Период собственных незатухающих колебаний в колебательном контуре определяется формулой Томсона
, (5)
а циклическая частота
. (6)
Колебания заряда происходят по гармоническому закону
, (7)
где – максимальный заряд на обкладках конденсатора;
– циклическая частота собственных колебаний;
– начальная фаза.
 |
На рисунках 3 и 4 представлены соответственно идеальный колебательный контур и график зависимости 
при 
.
Очевидно, что изменение напряжения между обкладками описывается таким же законом
(8)
где 
– максимальное напряжение между обкладками конденсатора.
Так как электрический ток характеризует скорость изменения заряда на обкладках конденсатора,
(9)
где 
– амплитуда силы тока.
Из выражений (7), (8), (9) следует, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на 
, т. е. ток достигает максимального значения в те моменты времени, когда заряд и напряжение на обкладках конденсатора равны нулю, и наоборот. Этот же вывод следует из анализа рис. 2 (а, б, в, г, д).
Идеальный колебательный контур (рис. 3), в котором происходят свободные незатухающие электромагнитные колебания, представляет собой электрическую цепь, состоящую из конденсатора емкостью и катушки индуктивности . Запишем для этого замкнутого контура второе правило Кирхгофа: сумма падений напряжений равна сумме э. д.с., действующих в контуре.
В контуре действует только одна э. д.с. – э. д.с. самоиндукции, следовательно
,
где 
– падение напряжения на конденсаторе;
– мгновенное значение заряда на обкладках конденсатора;
.
Так как 
, 
, то дифференциальное уравнение свободных незатухающих электромагнитных колебаний может быть записано в виде
,
,
где – собственная циклическая частота контура.
Уравнение колебаний принимает вид
и называется уравнением свободных незатухающих электромагнитных колебаний в дифференциальной форме.
Из математики известно, что решение этого уравнения имеет вид
,
т. е. соответствует формуле (7) и рис. 4 (при 
).
Таким образом, свободные незатухающие электромагнитные колебания являются гармоническими, а их период определяется формулой Томсона:
2. Закон сохранения и превращения энергии в идеализированном колебательном контуре
Исключительно важным является вопрос об энергии гармонических колебаний. С энергетической точки зрения гармоническое колебание представляет собой непрерывный процесс перехода кинетической энергии движущихся частей осциллятора в потенциальную энергию упругого элемента. Полная энергия гармонического осциллятора есть величина постоянная, так как для него потерь нет. Она равна либо максимальной кинетической энергии ( в момент прохождения положения равновесия) , либо максимальной потенциальной энергии (при амплитудном смешении). В задачах используются именно эти энергии, так как с их помощью можно оценить величину амплитуды и частоты собственных колебаний осциллятора.
Расчет энергии W гармонического осциллятора осуществляют стандартным образом. Для механических осцилляторов:
http://itm-x18.narod.ru/sem3/fizika_z3/01.html
http://pandia.ru/text/80/142/13117.php