Дифференциальное уравнение движения колебательной системы

Колебательное движение

Определение и основные понятия колебательного движения

Колебательное движение (колебание) — это любое движение или изменение состояния, которое повторяется во времени, соответственно повторяются значения физических величин, которые характеризуют данное движение или состояние.

Различные физические явления представляют собой колебания: звуковые колебания, электромагнитные, механические и т.д. У всех этих явлений существует общее в законах и математических методах, при помощи которых они описываются.

Колебательное движение называется периодическим, если переменные параметры этих колебаний повторяются через равные промежутки времени.

Колебания называются свободными, если они происходят в системе, на которую не действуют внешние силы (или действие их взаимно скомпенсировано).

Такая система один раз выводится из состояния равновесия. Если колебательная система консервативная, то рассеяния энергии при колебаниях нет. В таком случае свободные колебания являются незатухающими. Свободные незатухающие колебания, которые происходят под воздействием упругих сил, являются гармоническими.

Периодом незатухающих колебаний называют минимальный промежуток времени ($T$) по истечении которого происходит повторение значений всех физических параметров, которые характеризуют колебание.

Частотой колебаний ($\nu $) называют величину обратную периоду колебаний, это количество полных колебаний, которое совершает колебательная система:

Гармонические колебания

Самым простым типом колебаний считают гармонические колебания.

Колебания называют гармоническими, если изменения физической величины описывается при помощи закона синуса или косинуса.

Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:

где $A=s_$ — амплитуда колебаний (постоянна во времени); $<\omega >_0$ — циклическая (круговая) частота колебаний (с течением времени не изменяется); $\varphi $ — начальная фаза колебаний (фаза при $t=0$); $(<\omega >_0t+\varphi )$ — фаза колебаний. Величина $s$ изменяется $-A\le s\le $+A.

Те же самые колебания можно описать как:

За время равное периоду колебаний фаза изменяется на величину равную $2\pi $, поэтому:

Циклическая частота $<\omega >_0$ равна числу полных колебаний, которые совершаются колебательной системой за $2\pi $c:

Дифференциальное уравнение колебательного движения

Линейное дифференциальное уравнение гармонических колебаний представляет собой выражение:

Решениями уравнения (6) является выражения (2) и (3). Уравнение вида (6) называют уравнением гармонического осциллятора, а колебательную систему, которая совершает эти колебания гармоническим осциллятором (примерами гармонических осцилляторов являются: пружинный маятник, физический маятник, электрический колебательный контур).

Представление гармонических колебаний в комплексной форме

Сложение, разложение на составляющие и другие операции при изучении гармонических колебаний проще проводить, если представить уравнение гармонических колебаний в комплексной форме. При этом вместо действительной формы записи (2 и 3) используют комплексную:

Величина $\tilde$ является комплексной и не дает реального физического отклонения, которое характеризуется вещественной величиной $s$ (2,3). Но мнимую часть величины $\tilde$ можно рассматривать как действительной гармоническое колебание выраженное синусом. С другой стороны действительная часть (7) равная:

представляет собой вещественное гармоническое колебание. Поэтому гармонические колебания можно записывать в комплексном виде (7) и выполнять все требуемые расчёты. При получении результата нужно взять действительную или мнимую часть для перехода к физическим величинам.

Примеры задач на колебательное движение

Задание: Материальная точка, массой $m=<10>^<-4>$кг совершает колебания согласно закону: $x=0,05<\cos (20t)\ >$. Каково максимальное значение возвращающей силы, действующей на точку ($F_$)?

Решение:В соответствии со вторым законом Ньютона на материальную точку действует сила:

Так как колебания точки происходят по оси X, то получим:

Вычислим вторую производную от $x\left(t\right)=0,05$, имеем:

Подставим правую часть выражения (1.3) в (1.2) вместо соответствующей производной, учитывая массу точки получаем:

Максимальное значение косинуса равно единице, значит:

Ответ: $\left|F_\right|=2\cdot <10>^<-3>$Н

Задание: Нарисуйте траекторию колебательного движения точки, если она участвует одновременно в двух взаимно перпендикулярных колебаниях, которые описывают законы:

Решение:Определим, каким является уравнение колебательного движения точки в плоскости XY. Используем формулу косинуса двойного угла:

Из условия задачи:

Получаем, что $y$ равен:

Ответ: $y\left(x\right)=A-\frac<<2x>^2>$

Интегрированный урок «Приложение дифференциальных уравнений к колебательным системам»

Место урока в программе:

• физика: повторение видов колебаний и актуализация знаний перед изучением темы «Электромагнитные колебания»;
• математика: обзорный урок «Сложение гармонических колебаний» в разделе «Дифференциальные уравнения».

Урок предназначен для 11-х классов с углубленным изучением физики и математики.

Цели:

Обучающие:

• совершенствовать навыки решения экспериментальных задач;
• закрепить знания по теме «Механические колебания», дать математическое описание гармонических колебаний;
• повторить и обобщить материал по теме «Линейные дифференциальные уравнения первого порядка с постоянными коэффициентами»;
• описать гармонические колебания с помощью векторной диаграммы;
• изучить сложение гармонических колебаний в некоторых частных случаях.

Воспитательные:

• воспитание внимательности, аккуратности, трудолюбия;
• привитие навыков работы в группе, уважительного отношения к мнению товарищей.

Развивающие:

• развивать коммуникативные способности;
• развивать умение соотносить личностную самооценку с оценкой своей работы товарищами и реальной оценкой;
• развивать умение оценивать работу других и выставлять аргументированную отметку;
• развивать креативность мышления.

Тип урока:

• комбинированный с интеграцией математики и физики:
• физика: повторение и обобщение по теме «Механические колебания», решение экспериментальной задачи;
• математика: повторение гармонических колебаний, приложение дифференциальных уравнений к решению физических задач, изучение нового материала.

Оборудование: ПК, интерактивная доска, мультимедийный проектор, система интерактивного голосования PRS, цифровая лаборатория по физике «Архимед», набор пружин, набор грузов, измерительные инструменты.

Структура урока

1. Организационный момент — 2мин.
2. Актуализация знаний — 20мин.
3. Решение экспериментальной задачи — 20мин.
4. Эксперимент — 5мин.
5. Изучение нового материала — 15мин.
6. Эксперимент — 5мин.
7. Изучение нового материала — 10мин.
8. Домашнее задание — 2мин.
9. Итоги — 4 мин.
10. Обзор — 5мин.

Резерв времени — 2 мин.

Урок рассчитан на 90 мин.

Ход урока

1. Организационный момент.

Добиться внимания, сформулировать цели и задачи урока.

2. Актуализация знаний.

Рождённый пустыней,
Колеблется звук,
Колеблется синий
На нитке паук.
Колеблется воздух,
Прозрачен и чист,
В сияющих звёздах
Колеблется лист,

— так видит «Утро» Н. Заболоцкий. «Мир, в котором мы живём, удивительно склонен к колебаниям: Колеблются даже атомы, из которых мы состоим».

— Продолжите фразу: «Колеблется даже :» Ожидаемый ответ: сердце, голосовые связки :

— Какие колебания изображены на доске (слайд 2 Приложения 1)? Ожидаемый ответ: механические.

— Есть ли среди этих колебаний «лишние»? Ожидаемый ответ: электрические и типа «волны», т.к. неизвестен источник появления этих колебаний.

— Назовите виды механических колебаний и приведите примеры (слайд 3 Приложения 1).

Выполняется тест с помощью интерактивной системы голосования PRS (Приложение 2). За правильное решение вопроса можно получить 1 балл. Следовательно, максимальное количество баллов, которое может набрать пара, 8. В течение 30 секунд учащиеся выбирают ответ и нажимают на пульте кнопки от 1 до 5. В конце тестирования на экран выводится результат. Учащиеся вписывают количество правильных ответов в таблицу сопроводительного листа (Приложение 3).

Вопросы теста и правильные ответы приведены в Приложении 2.

3. Решение экспериментальной задачи.

Учащиеся разбиваются на 4 группы для решения экспериментальной задачи. Время работы в группах 20 мин.

Приборы и материалы: пружина, 2 груза массой по 100 г, секундомер и сантиметровая лента.

Постановка задачи:

1. Определить силу упругости, возникающую при деформации пружины.
2. Определить жесткость пружины.
3. Определить период колебаний пружинного маятника.
4. Определить частоту собственных колебаний системы.
5. Выдвинуть гипотезу о зависимости периода колебаний пружины от массы груза и жесткости пружины.
6. Ответить на предложенные вопросы в сопроводительном листе и записать результаты эксперимента в этот лист (Приложение 3).

По окончании эксперимента представитель каждой группы анализирует полученные результаты и заносит их в таблицу на доске (слайд 4 Приложения 1).

Полученные группами результаты комментируются учителем, оценивается их точность. Затем учащимся дается время оценить работу каждого члена группы, выставить отметку в таблице сопроводительного листа (Приложение 3) и обосновать ее.

4. Эксперимент.

Выбираем пружину наименьшей жесткости и с использованием цифровой лаборатории «Архимед», датчиков силы и расстояния, получаем график гармонического колебания.

— Выскажите гипотезу о законе, по которому осуществляются гармонические колебания.

5. Изучение нового материала.

Учащиеся работают в тетрадях параллельно с обсуждением нового материала. Слайд 5 Приложения 1.

Опишем движение тела функцией x(t), выражающей его отклонение от положения равновесия в момент времени t. В начальный момент времени тело находилось в положении равновесия, примем это положение за начало отсчета. Выведем тело из положения равновесия оттянув пружину вниз. Тело начинает двигаться под действием силы упругости, стремящейся вывести его из положения равновесия. По закону Гука

,

где k — коэффициент упругости пружины, x — отклонение от положения равновесия.

С другой стороны, согласно второго закона Ньютона,

,

где m — масса тела, a — ускорение.

Вопрос к аудитории: дайте математическую интерпретацию ускорения. Ожидаемый ответ: ускорение — это вторая производная от перемещения по времени.

Приравнивая силы, получим дифференциальное уравнение , — уравнение гармонического колебания.

Вопрос к аудитории: дайте физическую интерпретацию частного . Ожидаемый ответ: это частное является квадратом частоты колебания.

.

С учетом последнего уравнение гармонического колебания примет вид , а его общим решением является функция , c₁,c₂ — const.

При изучении гармонических колебаний с точки зрения физики движение тела рассматривалось как движение по косинусоиде. Нет ли здесь противоречия с математической моделью? Ожидаемый ответ: нет, так как с помощью тригонометрических формул можно свести это уравнение к уравнению, содержащему только одну из тригонометрических функций (синус или косинус).

Приведем полученное решение дифференциального уравнения к требуемому виду и дадим физическую интерпретацию коэффициентов полученной функции.

Воспользуемся формулой , где , . Тогда или ,

где — амплитуда колебания, j ₀ — начальная фаза.

Исходя из экспериментальных данных х(0)=А, поэтому , следовательно .

Амплитуда и частота определены вами экспериментально. Запишите уравнение движения колеблющегося тела в проведенном вами эксперименте в сопроводительный лист и тетрадь.

Если бы перед нами стояла задача отыскания коэффициентов , то для ее решения пришлось бы находить решение системы уравнений

Так как , то с₁=0, с₂=А.

Переход к слайду 6 Приложения 1.

Если в начальный момент времени грузу была сообщена начальная скорость V₀, то уравнение гармонического колебания имеет вид:

,

где , причем знак зависит от направления начальной скорости.

В реальных условиях любая колебательная система находится под действием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения атомов и молекул, и колебания становятся затухающими.

Скорость затухания зависит от величины сил трения. Частота свободных затухающих колебаний зависит от скорости затухания: чем больше сила трения, тем ниже частота (это заметно при достаточно большой силе трения).

График затухающего колебания приведен на рисунке 6.

Работа в группах.

Опишите гармонические колебания вашей пружины с помощью уравнений изменения координаты и силы от времени. Ответ занесите в таблицу сопроводительного листа (Приложение 3) и таблицу на доске (слайд 7 Приложения 1).

6. Эксперимент.

Выбираем пружину наибольшей жесткости и с использованием цифровой лаборатории «Архимед», датчиков силы и расстояния, получаем колебания в разных направлениях и проводим анализ получившихся графиков.

7. Изучение нового материала.

Мы уже убедились, что тело колеблется по закону гармонических колебаний. Почему при проведении опыта получен график, отличающийся от графика функции, описывающей гармоническое колебание? Ожидаемый ответ: происходит наложение нескольких гармонических колебаний, осуществляющихся в разных направлениях.

В последнем опыте колебание происходило одновременно в нескольких направлениях. В этом случае гармонические колебания накладываются друг на друга, для получения уравнения движения тела его колебания по разным направлениям приходится складывать. Наиболее часто рассматривают сложение двух колебаний в следующих ситуациях:

Сложение двух колебаний

— одного направления:

• одинаковой частотой и разными амплитудами,
• с одинаковыми амплитудами с разными частотами,
• с разными амплитудами и частотами;

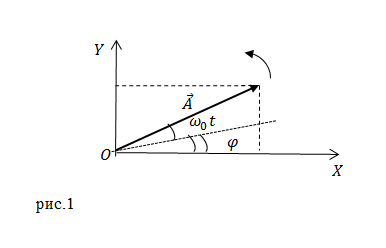
Рассмотрим движение материальной точки против часовой стрелки по окружности радиуса А с центром в начале координат (слайд 9 Приложения 1). Тогда координаты точки в любой момент времени выражаются через угол поворота j по формулам

Угол поворота j в том случае, когда в начальный момент времени t=0 точка М находилась на оси Ох, равен

j =w t=.

Если в начальный момент времени тело не находится в точке А(а;0), то необходимо добавить начальный угол j ₀ (начальная фаза), т.е.

где — фаза колебания.

Таким образом, проекции точки М на оси Ох и Оу совершают гармонические колебания, имеющие одинаковые направления и частоты. Поэтому гармоническое колебание проекции точки М на оси Ох можно интерпретировать как колебание проекции вектора , равномерно вращающегося вокруг начала координат, на ось Ох. Эта проекция называется векторной диаграммой гармонического колебания с амплитудой А, частотой w и начальной фазой j ₀.

Сложение колебаний одинаковых частот

Рассмотрим сумму двух колебаний, заданных уравнениями (слайд 10 Приложения 1)

,

с одинаковой частотой и разными амплитудами.

Сумму колебаний можно рассматривать как сумму векторов . Так как векторы вращаются с одинаковой угловой скоростью, то весь параллелограмм вращается как жесткая фигура, тогда его диагональ вращается с той же угловой скоростью, следовательно, абсцисса точки М совершает гармонические колебания, причем по теореме косинусов из треугольника ОММ₁

,

,

поэтому — уравнение суммы двух гармонических колебаний с одинаковой частотой.

Следующий слайд 11 Приложения 1.

1. Колебания находятся в фазе: j ₀₂=j ₀₁. В этом случае колебания взаимно усиливаются

2. Колебания находятся в противофазе: j ₀₂ — j ₀₁=+ p . Колебания частично гасят друг друга:

Если амплитуды равны, то колебания гасятся полностью.

Сложение колебаний разных частот

Если частоты колебаний разные, то результирующий вектор пульсирует по величине и вращается с непостоянной скоростью. В этом случае результирующее колебание не является гармоническим.

Если амплитуды складываемых колебаний и начальные фазы равны, т.е. , то уравнение суммы этих колебаний имеет вид

.

Период такого колебания вычисляется по формуле .

С точки зрения физики такая кривая называется виброграмма, а явление вибрация.

8. Домашнее задание.

Найти сумму гармонических колебаний , . Рассчитать по данным уравнениям период, частоту, амплитуду и построить графики (слайд 13 Приложения 1).

9. Итоги урока

Работа в группах.

Учащиеся оценивают работу товарищей при изучении нового материала по математике, выставляют оценки в таблицу сопроводительного листа (Приложение 3), затем учитель подводит итоги и выставляет отметки.

Учащиеся формулируют теоретические и экспериментальные задачи, решенные на уроках, и основные результаты. Ответ учащихся комментируется учителем.

10. Обзор.

Этот урок был проведен в рамках РМО по теме «Использование информационных технологий на уроках физики и математики» и получил положительную оценку со стороны преподавателей района.

Замечание. При подготовке презентации в ряде случаев использовались рисунки и анимации, найденные на различных сайтах. К сожалению, ссылки на настоящий момент не сохранились.

Свободные и вынужденные механические колебания

Вы будете перенаправлены на Автор24

Движения или процессы, которые имеют определенную повторяемость, называют колебаниями.

Физическая природа колебаний может быть различной, в этой связи различают:

• механические колебания;
• электромагнитные колебания;
• квантовые;
• смешанные (электромеханические).

Разные по природе колебания описываю при помощи одинаковых параметров и одинаковых уравнений. Общим подходом исследования механических и электромагнитных колебаний пользовались разные ученые –физики, например, Д.У. Рэлеей и А.Г. Столетов, П.Н. Лебедев.

Свободные гармонические колебания

Колебания считают свободными (собственными) в том случае, если они выполняются только за счет энергии, которая была сообщена колебательной системе в начальный момент времени и далее внешние воздействия на эту систему отсутствуют.

Самым простым для математического описания видом колебательных процессов стали гармонические колебания.

Гармоническими колебаниями называют колебания, у которых изменение колеблющегося параметра происходит по закону синуса или косинуса:

$s=s_m cos (\omega_0 t+\varphi) (1),$

где $s_m$ — наибольшее значение переменного параметра $s$ (амплитуда); $\omega_0$ — циклическая частота колебаний; $\varphi$ — начальная фаза колебаний; $(\omega_0 t+\varphi)$ — фаза колебаний в момент времени $t$. $- s_m

Гармонические колебания рассматриваются подробно поскольку:

1. колебания, которые происходят в реальной действительности часто близки к гармоническим;
2. разные периодические процессы можно представлять как сумму гармонических колебаний.

Состояния колебательной системы, выполняющей гармонические колебания, повторяются спустя промежуток времени, который именуют периодом колебаний ($T$). За время, равное периоду, фаза колебаний изменяется на величину, равную $2\pi$:

Готовые работы на аналогичную тему

$(\omega_0 (t+T)+\varphi)=(\omega_0 t+\varphi)+2\pi (2)$,

в результате можем записать:

Величину, обратную периоду, называют частотой колебаний:

Частота – это физическая величина, равная количеству полных колебаний которое система совершает за единицу времени. При этом выполняется равенство:

$\omega_0 = 2\pi \nu (5).$

Дифференциальные уравнения свободных гармонических колебаний

Поведем дифференцирование по времени выражения (1), тогда первая производная равна:

$\frac