ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛ В ВЯЗКОЙ СРЕДЕ»
Цель работы:на примере движения тела шарообразной формы изучить основные закономерности движения в вязкой среде.
Литература
1. Савельев И.В. Курс общей физики, т.1. Механика и молекулярная физика.
2. Стрелков С.П. Механика.
3. Александров Н.В., Яшкин А.Я. Курс общей физики. Механика.
4. Архангельский М.М. Курс физики. Механика.
Вопросы для допуска к работы
а) знать следующие теоретические вопросы:
1. Понятие пограничного слоя. Чем определяется толщина пограничного слоя? Ламинарное и турбулентное движение.
2. Силы, действующие на тело при его движении в вязкой среде. Определяющие формулы сил, которые действуют на тело.
3. Уравнение движения тела. Характер движения тела на отдельных участках.
4. Число Рейнольдса: его физический смысл и определяющая формула.
б) иметь в протоколе следующие расчетные формулы:
1. Формулу для расчета скорости движения шарика при условии равномерного движения.
2. Формулу, по которой можно оценить число Рейнольдса, зная геометрические размеры, массу шарика и характеристики среды.
3. Формулы для расчета объема тел и площади «миделя».
4. Формулы для оценки погрешности.
Р.S. В расчетные формулы должны входить только те величины, которые могут быть измерены в процессе выполнения работы.
Краткая теория вопроса
На тело, движущееся в вязкой среде, действует сила сопротивления, величина которой зависит от размеров и формы тела, скорости его движения относительно среды и свойств самой среды. Как показал Л. Прандтль, процессы, обуславливающие появление силы сопротивления, в значительной мере определяются явлениями, происходящими в пограничном слое и характером вихрей. Вычисление силы сопротивления является исключительно сложной задачей и можно лишь оценить порядок этой силы.
В общем случае полная сила сопротивления движению тела в вязкой среде складывается из двух компонент: сопротивления трения и сопротивления давления. Первое слагаемое определяется силами внутреннего трения, возникающим за счет градиента скорости в пограничном слое, второе — разностью давлений на передней и задней кромках обтекаемого тела и связано с турбулентным (вихревым) движением жидкости.
Стокс установил, что при небольших скоростях и размерах тел модуль силы сопротивления трения определяется формулой:
где h — динамическая вязкость среды, V — скорость движения тела, L — характерный размер тела и k — коэффициент пропорциональности, который зависит от формы тела. Для шара k = 6p. Исходя из формулы (1) выражение для определения модуля силы сопротивления трения имеет вид:
Модуль силы сопротивления давления определяется формулой:
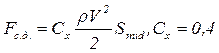
где r — плотность среды, V — скорость движения тела, Cx — характеристический коэффициент обтекаемости тела, зависящий от формы тела, Smid — площадь «миделя», под которой понимают наибольшую площадь сечения тела плоскостью, перпендикулярной к потоку.
Для оценки вклада той или иной силы в величину полной силы сопротивления движению в вязкой среде введено число Рейнольдса Re, которое определяется как отношение силы сопротивления давления к силе трения. Так при Re£0,5 (ламинарное движение) учитывают только силу сопротивления трения. При 0,5 1, т.е. турбулентных (вихревых) течений, учитывают только
силу сопротивления давления.
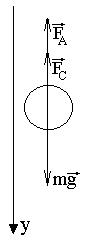
Найдем уравнения, описывающие движение тела в вязкой среде, т.е. решим основную задачу динамики. Рассмотрим это решение на примере падения шарика в вязкой среде (см. рис.). Динамическое уравнение движения может быть записано в виде:
В проекции на вертикальную ось Y это же уравнение записывается так:
Из трех сил лишь одна является переменной — это сила сопротивления, величина которой быстро изменяется с увеличением скорости. Естественно, что с течением времени ускорение, с которым движется тело, будет уменьшаться, и наступит такой момент, когда оно станет равным нулю. Начиная с этого момента тело будет двигаться равномерно с постоян ной скоростью Vуст, величину которой можно найти из уравнения движения при условии, что а=0.
 |
| Рис. 1 |
В зависимости от того, какая сила сопротивления преобладает значение Vуст будет различным.
Законы движения, описывающие движение тела, можно найти, решая дифференциальное уравнение вида:
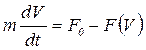
где
Список заданий
Задание 1: Экспериментально определить скорость установившегося движения шарика в глицерине и число Рейнольдса. Необходимые для расчета данные взять из справочной литературы или определить экспериментально.
Задание 2: Используя результаты работы записать зависимость V(t), Y(t), a(t).
Вопросы для зачета
1. Понятие пограничного слоя. Чем определяется толщина пограничного слоя?
2. Какое движение называют ламинарным, турбулентным?
3. Какие силы действуют на тело, движущееся в вязкой среде?
4. Каковы причины появления сил сопротивления давления и сопротивления трения?
5. Каков физический смысл и размерность коэффициента вязкости
6. Физический смысл числа Рейнольдса.
7. Напишите уравнение движения тела. Каков характер движения тела на отдельных участках?
8. Качественные графики зависимости скорости и ускорения тела, падающего в вязкой среде, от времени.
МУ 4866: Изучение сил вязкого трения
Лабораторная работа 1-8: Изучение сил вязкого трения
Цель работы: изучение явления вязкого трения и одного из методов определения вязкости жидкостей.
Элементы теории и метод эксперимента
При движении тел в жидкостях и газах на тела действуют силы внутреннего трения. Эти силы присущи всем реальным жидкостям и газам и составляют основу понятия вязкости. Вязкость − важная физическая характеристика веществ. Значение вязкости приходится учитывать при перекачивании жидкостей и газов по трубам (нефтепроводы, газопроводы), вязкость расплавленного стекла определяет процесс его выработки, большую роль играет вязкость в процессах выплавки металлов и т.д.
В физике явление вязкости относится к так называемым явлениям переноса. К ним также относятся явления диффузии (на молекулярно-кинетическом уровне объяснение явления связано с переносом вещества – атомов или молекул) и теплопроводности (перенос энергии при столкновениях молекул). С точки зрения молекулярно-кинетической теории вязкость объясняется переносом импульса при взаимодействии молекул.
При ламинарном течении жидкости или газа между слоями, движущимися с различной скоростью, действуют силы, обусловленные вязкостью. Если два слоя
площадью S (рис. 1) находятся на расстоянии ∆z и движутся с различными скоростями, так что ∆v = v2 – v1, между ними возникает сила вязкого трения, пропорциональная градиенту скорости ∆v/∆z в направлении, перпендикулярном к направлению течения, и площади слоев S. Этот эмпирический закон открыл Ньютон (Newton, 1687 г.):
где коэффициент η по определению называется вязкостью или коэффициентом внутреннего трения.
Из формулы (1) видно, что вязкость измеряется в паскаль-секундах (Па·с). Используют и более мелкую единицу вязкости − пуаз (П), названную так в честь французского физика Пуазейля: 1 Па·с = 10 П.
Движение жидкости (газа) в круглой трубе. Рассмотрим ламинарное течение жидкости (газа) в трубе радиусом R (рис. 2).
Выделим в этой трубе трубку длиной L меньшего радиуса r. На внешнюю поверхность этой трубки будет действовать сила, обусловленная вязкостью:
При равномерном движении эта сила должна быть равна равнодействующей сил давления, влияющих на торцы этого малого цилиндрика, ограничивающего поверхность трубки:
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Решением этого уравнения с учетом того, что вблизи стенок трубы скорость течения равна нулю, будет:
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Отсюда скорость течения на оси трубы:
С учетом этого можно записать:
Таким образом, изменение скорости по сечению трубы получается параболическим.
Найдем расход (поток) жидкости Q = ΔV/Δt , т.е. объем жидкости, протекающей через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца шириной dr (рис.3).
Через кольцо радиусом r за секунду пройдет объем жидкости, равный произведению площади кольца 2πrdr на скорость течения в точках, находящихся на расстоянии r от оси трубы:
Полный поток получается интегрированием:
Из (9) и (6) получим формулу для потока:
Формула (10) называется формулой Пуазейля (Poiseuille, 1840). Согласно этой формуле поток жидкости пропорционален перепаду давления на единице длины трубы, пропорционален четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости.
Вязкость газов по молекулярно-кинетической теории (MKT). В газах вязкость обусловлена столкновением молекул, в жидкостях − межмолекулярным взаимодействием, ограничивающим подвижность молекул.
Рассмотрим два слоя газа, движущихся с разными скоростями (рис. 1). Если температура газа всюду одинакова, то средняя скорость движения молекул равна:
где т − масса молекулы.
Так как молекула может двигаться по шести независимым направлениям в пространстве, то площадку S за единицу времени пересечет N = unS/6 молекул, где п − концентрация молекул. Так как молекулы сталкиваются, проходя в среднем определенное расстояние, приблизительно равное средней длине свободного пробега λ, то импульс, связанный с направленным движением слоев со скоростями v1 и v2, будет передаваться слою, находящемуся между ними, если расстояние до него равно длине свободного пробега молекул, при этом изменение импульса молекул среднего слоя за время ∆t будет
Так как v(z) есть непрерывная функция координаты z, можно считать, что v2=v(z+λ), а v1=v(z-λ). Если размеры сосуда, в котором находится газ, много больше длины свободного пробега, то, полагая что λ можно считать очень малым изменением аргумента функции v(z), из определения производной следуют приближенные равенства:
Если подставить эти выражения в формулу для изменения импульса и учесть, что по второму закону Ньютона изменение импульса равно импульсу силы (∆p = F∆t), то из определения понятия коэффициента внутреннего трения с учетом того, что произведение массы молекулы на их концентрацию есть плотность газа (ρ = nm), для вязкости получается выражение:
Это выражение можно преобразовать. По молекулярно-кинетической теории длина свободного пробега молекул
где d − эффективный диаметр молекулы.
Подставив u и λ в выражение для вязкости, получим
Видим, что вязкость зависит от параметров молекулы (т и d) и от температуры газа, а от давления и плотности не зависит.
Значения вязкости некоторых жидких и газообразных веществ даны в приложении. Расплавленные металлы имеют вязкость того же порядка, что и обычные жидкости.
Так как при повышении температуры подвижность молекул увеличивается, вязкость при этом уменьшается (на примере воды это показано в приложении).
Особыми вязкостными свойствами обладает жидкий гелий. При температуре ниже 2,172 К (а температура перехода его в жидкое состояние при нормальном атмосферном давлении, т.е. температура кипения, равна 4,4 К, и при дальнейшем понижении температуры он остается жидкостью, не переходя в твердое состояние) он переходит в сверхтекучее состояние, в котором вязкость равна нулю. Это явление открыл в 1938 г. П.Л.Капица (Нобелевская премия, 1978).
Метод Стокса
Одним из методов измерения вязкости веществ (вискозиметрии) является метод падающего
шарика, или метод Стокса (Stokes, 1851 г.). Английский физик Стокс показал, что на шарик, движущийся со скоростью v в вязкой среде, действует сила вязкого трения, равная F=3πηvd , где d − диаметр шарика.
Рассмотрим движение шарика при его падении. По второму закону Ньютона (рис. 4)
где А — сила вязкого трения, FA =1/6*(ρжπd 3 g) — сила Архимеда, mg= 1/6*(ρπd 3 g) — сила тяжести, ρж и ρ — плотности жидкости и материала шариков соответственно. Решением этого дифференциального уравнения будет следующая зависимость скорости от времени:
где v0 — начальная скорость шарика, а
— скорость установившегося движения (при t>>τ). Величина τ= ρd 2 /η есть время релаксации.
Эта величина показывает, насколько быстро устанавливается стационарный режим движения. Обычно считают, что при t ≈ 3τ движение практически не отличается от стационарного. Следовательно, измерив скорость vy, можно рассчитать вязкость жидкости.
Условие ламинарности движения жидкости определяется значением безразмерного параметра − числом Рейнольдса:
где d − характерный размер движущегося тела (в данном случае диаметр шарика). Формула Стокса применима для значений R Порядок выполнения работы
- Измерить с помощью штангенциркуля внутренний диаметр сосуда, с помощью линейки − расстояние между горизонтальными метками на сосуде и с помощью микрометра − диаметры всех шариков, используемых в эксперименте. Ускорение силы тяжести считать равным 9,8 м/с 2 . Плотность жидкости и плотность вещества шариков указаны на лабораторной установке. Результаты занести в таблицу.
- Опуская поочередно шарики в жидкость, измерить время прохождения каждого из них на отрезке пути между метками. По формуле (20) вычислить вязкость жидкости η. Результаты занести в таблицу.
- Оценить погрешность результатов измерений и получить окончательный результат для значения η.
4. По формуле (19) определить значение числа Рейнольдса для одного из опытов и сделать вывод о применимости формулы Стокса.
5. Оценить путь, пройденный шариком до установления стационарного режима. Очевидно, что за время t пройденный путь определяется интегралом:
Показать, что при t = 3τ путь s = 2vyτ, и оценить эту величину.
Сравнить полученное значение с расстоянием, проходимым шариком от поверхности жидкости до верхней метки, и сделать вывод, можно ли к моменту прохождения шариком верхней метки считать его движение установившимся.
Приложение
Вязкости некоторых веществ (в мкПа·с)
Вязкость воды при разных температурах
| Температура, °С | 0 | 20 | 40 | 60 | 80 | 100 |
| η | 1790 | 1010 | 660 | 470 | 360 | 280 |
Вязкость некоторых жидкостей (при 20 о С)
| Ацетон | Бензин | Глицерин | Кастор. масло | Скипидар | Спирт |
| 330 | 650 | 1,5·10 6 | 0,99·10 6 | 1500 | 1200 |
Вязкость некоторых газов (при 20 о С)
| Азот | Водород | Воздух | Кислород | Окись углерода | Углекислый газ |
| 17,5 | 8,8 | 18,1 | 20,2 | 18,4 | 16,0 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Объяснить молекулярно-кинетический механизм явления внутреннего трения.
- Дать определение понятия вязкости и единиц ее измерения.
- Какие измерения вносят наибольшую погрешность в результат косвенного измерения вязкости жидкости в ваших опытах?
- Что такое ламинарное и турбулентное течения?
- Имеется 2 шарика из одинакового материала, но различного размера. Какой шарик будет быстрее падать в вязкой жидкости? Когда шарик быстрее падает в вязкой жидкости: в узком сосуде или в широком?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1979 (и по- следующие издания). – С. 252-256, 258-261, 400-404.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. − М.: Высш.шк., 2001. – С. 62-66.
Изучение сил вязкого трения: методические указания к лабораторной работе / Рязан. гос. радиотехн. ун-т; сост.: Ю.В. Черкасова, А.С. Иваников. – Рязань, 2015. – 8 с.
Содержат элементы теории и метод определения вязкости жидкостей. Предназначены для студентов всех специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 4. Библиогр.: 2 назв.
Вязкое трение, ламинарное течение, метод Стокса, число Рейнольдса
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Изучение сил вязкого трения
Составители: Черкасова Юлия Вадимовна
Иваников Александр Сергеевич
Редактор Р.К. Мангутова Корректор С.В. Макушина
Подписано в печать 02.02.15. Формат бумаги 60 x 84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
Кратко о гидродинамике: уравнения движения
Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.
В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.
Понятие сплошной среды
В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.
Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.
Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.
Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.
Уравнение неразрывности. Закон сохранения массы
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:
И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):
где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.
В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:
Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.
Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:
Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:
Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:
которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.
Уравнение Эйлера. Закон сохранения импульса
Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.
Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:
При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:
- конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
- давления окружающих элементов жидкости
- просто за счёт внешних сил, например — от силы тяжести.
Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:
Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:
Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.
В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:
Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.
Учёт вязкости. Уравнение Навье-Стокса
Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.
Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:
По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:
Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:
Оно допускает любой закон для вязкости.
Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:
в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:
где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости
носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:
Точные решения
Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.
Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.
Потенциальные течения
Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:
Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.
Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):
которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.
Простые течения вязкой жидкости
Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.
Сдвиговое течение Куэтта
Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.
В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:
Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.
Течение Пуазейля
Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:
На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.
Стекание слоя жидкости по наклонной плоскости
Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.
В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.
http://russianstuds.ru/mu-4866-izuchenie-sil-vyazkogo-treniya/
http://habr.com/ru/post/171327/






