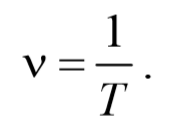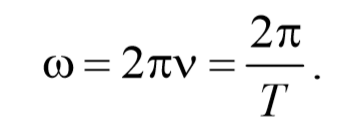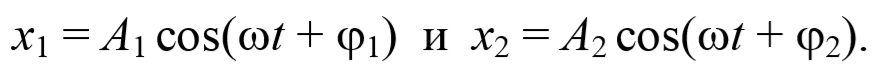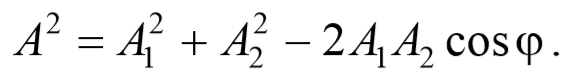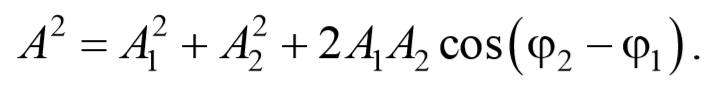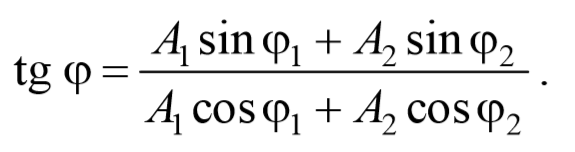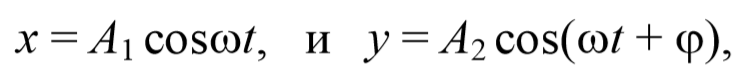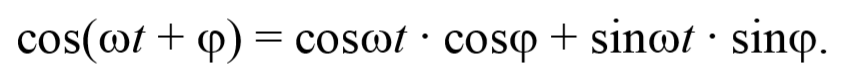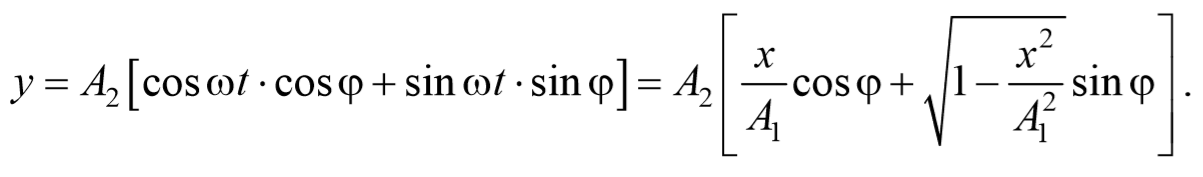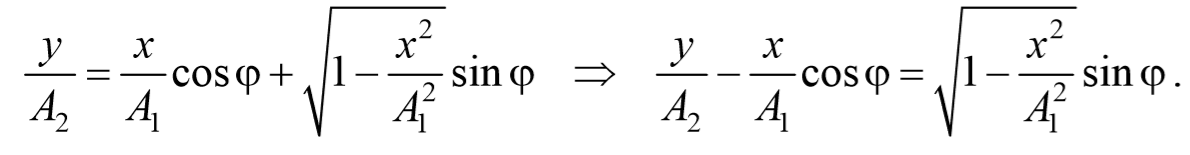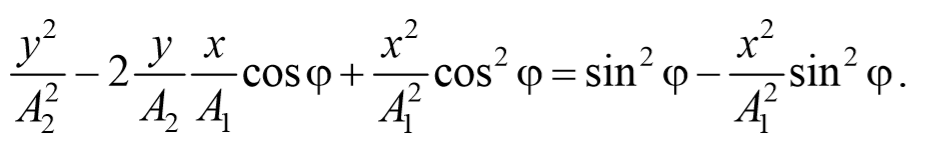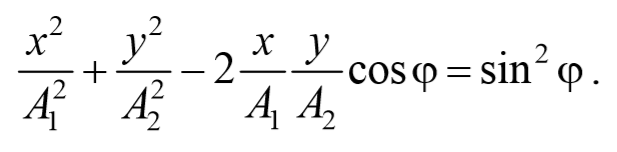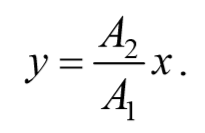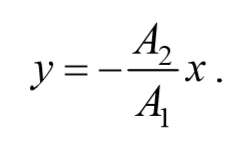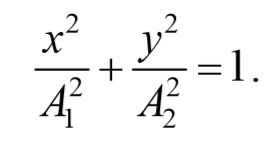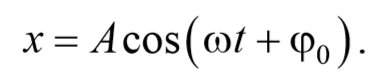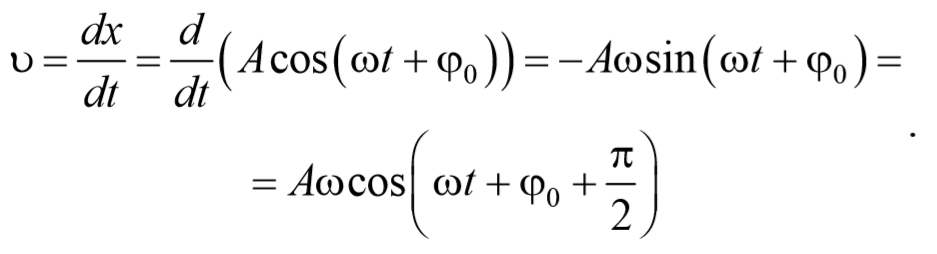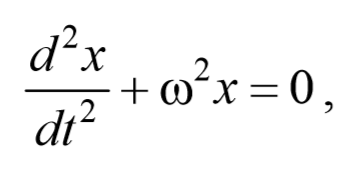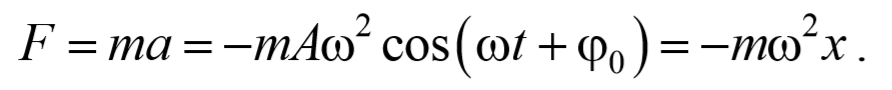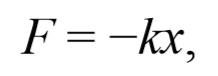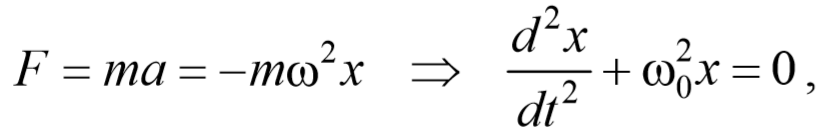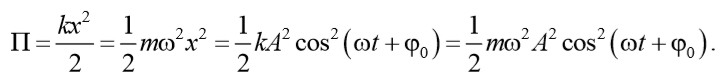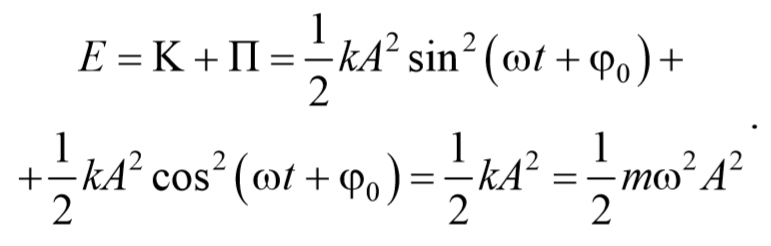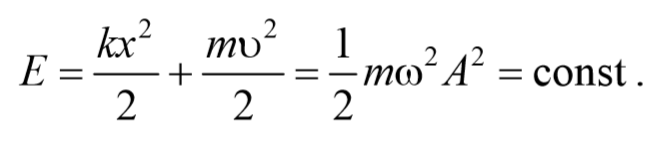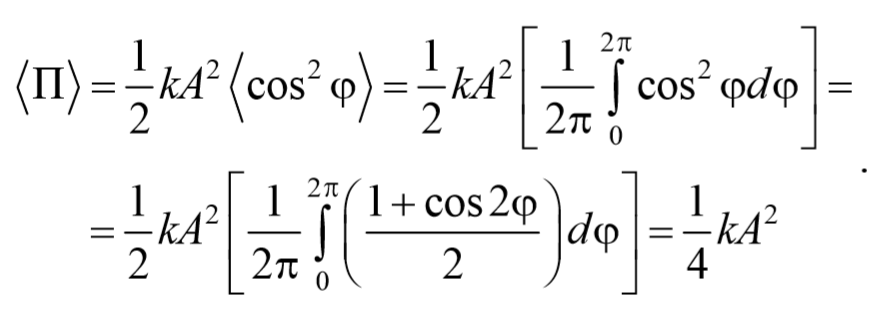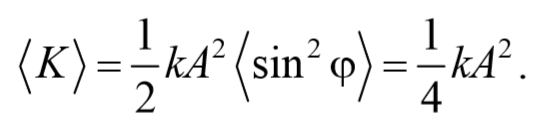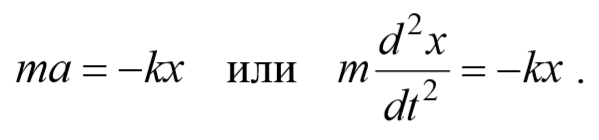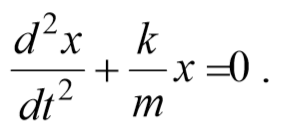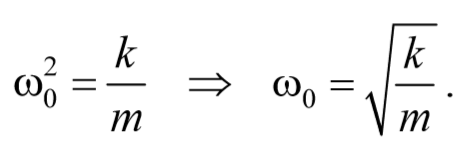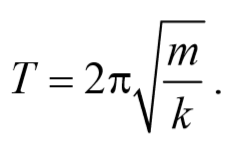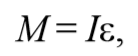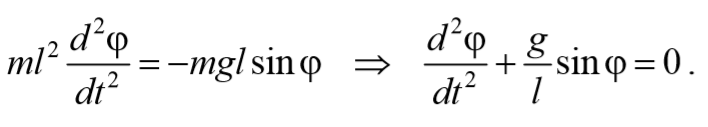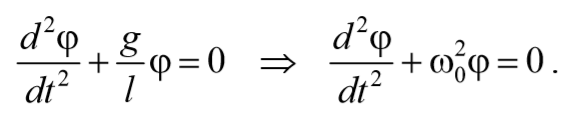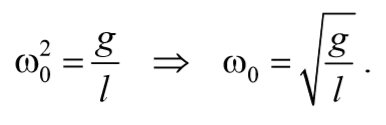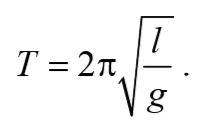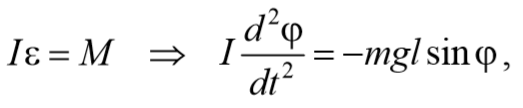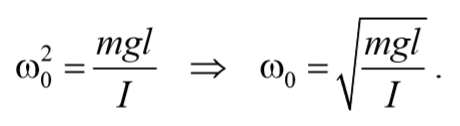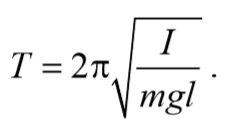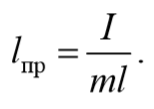Дифференциальное уравнение гармонических колебаний и их анализ

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

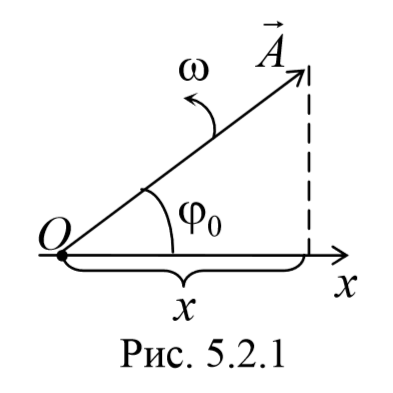
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$x\over A_1$$ , а sinωt= $$\sqrt<1-cos^2 ωt>=\sqrt<1-x^2\over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= \sqrt+A_2<^2>>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой

3) Разность фаз равна ± $$π\over 2$$ [φ=± $$π \over2$$ ] . Тогда

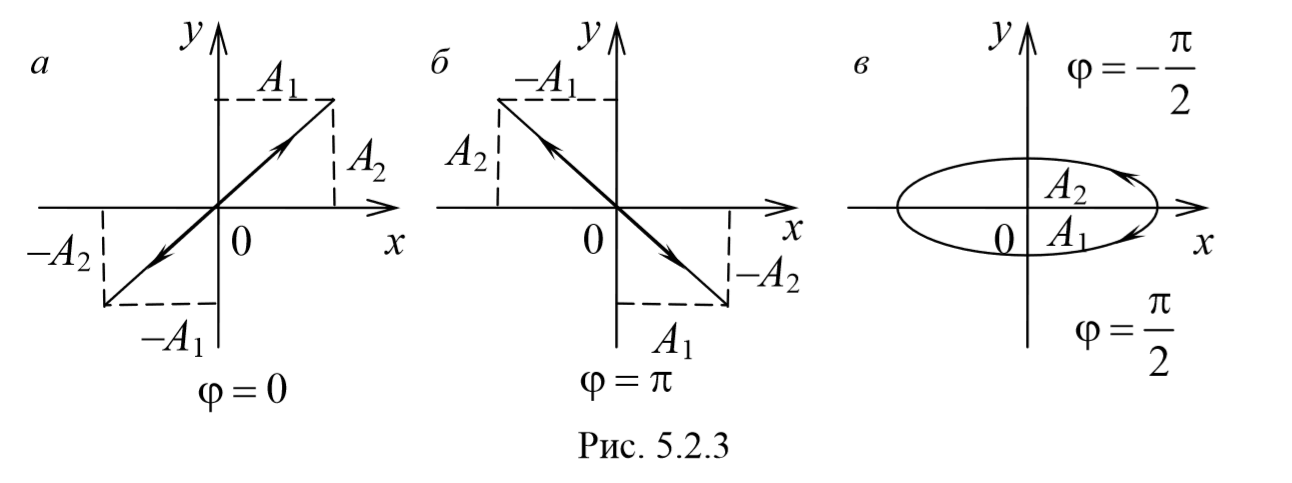
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$π\over 2$$ и φ=- $$π\over 2$$ отличаются направлением движения. Если φ=+ $$π\over 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$π\over 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

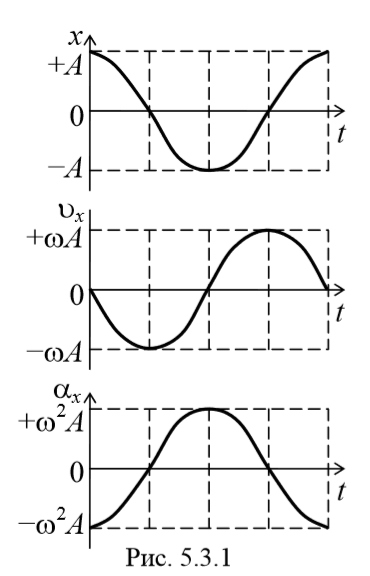
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

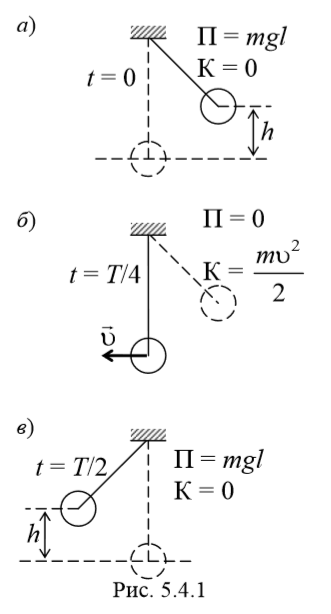
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

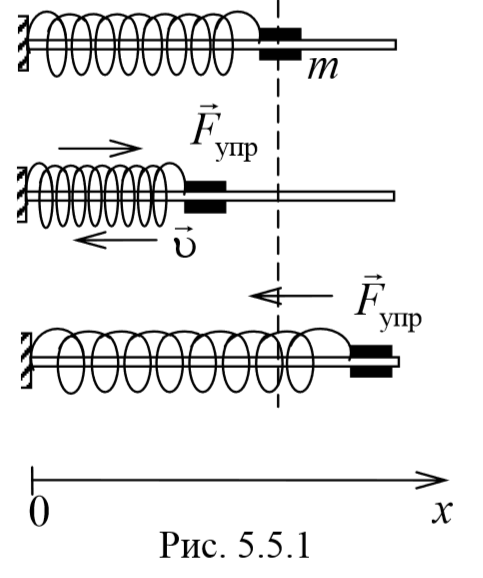
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2π\over ω_0$$ , то период колебаний пружинного маятника

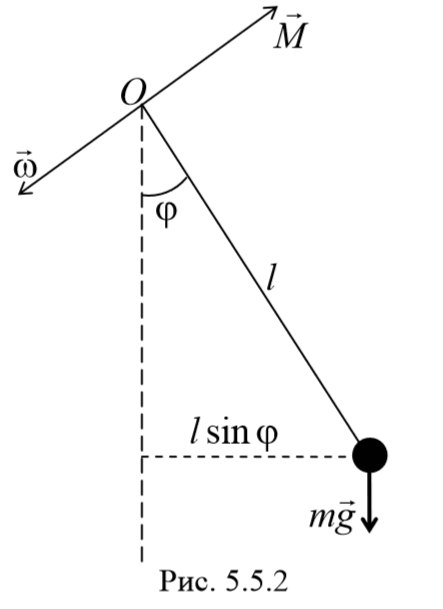
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φ\over dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

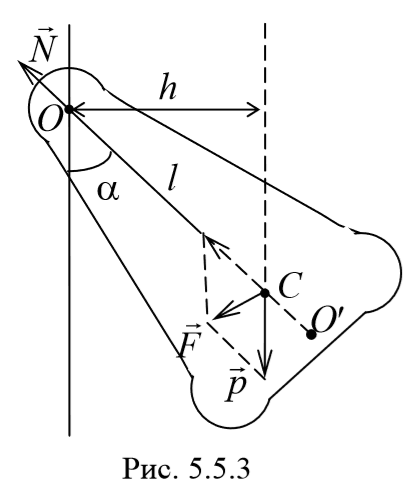
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$\sqrt$$ и T=2π $$\sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Гармоническое колебание. Уравнение. Автоколебания. Механический резонанс

Содержание:

Предмет:	Физика
Тип работы:	Реферат
Язык:	Русский
Дата добавления:	04.06.2019

Данный тип работы не является научным трудом, не является готовой работой!
Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала при самостоятельной подготовки учебной работы.

Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!

По этой ссылке вы сможете найти много готовых тем для рефератов по физике:

Посмотрите похожие темы возможно они вам могут быть полезны:

Введение:

Механические колебания: гармонические, затухающие и вынужденные колебания Колебания называются процессами, которые отличаются различной степенью повторяемости (колебание маятника часов, колебания струны или ножки камертона, напряжение между пластинами конденсатора в радиосвязи, функция сердца).

В зависимости от физической природы повторяющегося процесса различаются колебания: механические, электромагнитные, электромеханические и т. Д. Будем рассматривать механические колебания. Колебания, происходящие в отсутствие трения и внешних сил, называются внутренними; их частота зависит только от свойств системы. Простейшими являются гармонические колебания, то есть такие колебания, в которых колеблющаяся величина (например, отклонение маятника) изменяется во времени в соответствии с законом синуса или косинуса.

Дифференциальное уравнение гармонического колебания

Рассмотрим простейшую колебательную систему: шар массы m подвешен на пружине. В этом случае сила упругости F1 уравновешивает силу тяжести mg. Если вы переместите шар на расстояние x, то на него будет действовать большая сила упругости (F1 + F). Изменение силы упругости в соответствии с законом Гука пропорционально изменению длины пружины или смещению шарика х: F = -kx, (1) где k — жесткость пружины. Знак «-» отражает тот факт, что смещение и сила имеют противоположные направления.

Сила F обладает следующими свойствами: она пропорциональна смещению шара из положения равновесия; оно всегда направлено в положение равновесия.

В нашем примере сила по своей природе эластична. Может случиться так, что сила другого происхождения обнаруживает один и тот же паттерн, то есть оказывается, что она равна — kx. Силы такого типа, неэластичные по своей природе, но сходные по свойствам с силами, возникающими при малых деформациях упругих тел, называются квазиупругими.

Поскольку k и m являются положительными величинами, их отношение может быть приравнено к квадрату определенного значения 0, то есть мы можем ввести обозначение.

Таким образом, движение шара под действием силы вида описывается линейным однородным дифференциальным уравнением второго порядка.

Подстановкой легко проверить, что решение уравнения имеет вид

где (0 t + 0) = — фаза колебаний; 0 — начальная фаза при t = 0; 0 — круговая частота колебаний; А это их амплитуда.

Итак, смещение x изменяется со временем в соответствии с законом косинуса.

Следовательно, движение системы под действием силы вида f = — kx является гармоническим колебанием.

Гармоническая Энергия

Выясним, как со временем меняются кинетическая Еk и потенциальная Еп энергия гармонического колебания. Кинетическая энергия равна:

Мы находим потенциальную энергию из формулы потенциальной энергии для упругой деформации и используя (3):

Сложив (4) и (5) с учетом соотношения, получим:

Таким образом, полная энергия гармонической вибрации остается постоянной в отсутствие сил трения, во время колебательного процесса кинетическая энергия переходит в потенциал и наоборот.

Затухающие колебания

Колебания, возникающие в системе в отсутствие внешних сил (но при наличии потерь на трение или излучение), называются свободными. Частота свободных колебаний зависит от свойств системы и интенсивности потерь.

Наличие трения приводит к затуханию колебаний. Колебания с уменьшающейся амплитудой называются затухающими.

Мы ограничимся рассмотрением малых колебаний, тогда скорость системы будет мала, а на низких скоростях сила сопротивления пропорциональна величине скорости:

где r — коэффициент сопротивления среды. Знак «-» связан с тем, что Ftr и V имеют противоположные направления.

Решение этого уравнения существенно зависит от знака разности: 2 = 02 -2, где — круговая частота затухающих колебаний.

Пунктирная линия показывает изменение амплитуды: A = A0e-t.

Период затухающих колебаний зависит от коэффициента трения и равен:

При небольшом сопротивлении среды (2 2) период практически равен. С увеличением коэффициента затухания период колебаний увеличивается.

Из формулы, выражающей закон уменьшения амплитуды колебаний, мы можем убедиться, что отношение амплитуд, отделенных друг от друга интервалом в один период (T), остается постоянным на протяжении всего процесса затухания. Действительно, амплитуды колебаний, разделенные интервалом в один период.

Это соотношение называется декрементом затухания.

Величина натурального логарифма часто принимается за меру затухания.

Это значение называется логарифмическим декрементом ослабления за период.

При сильном затухании 2> 02 из формулы следует, что период колебаний является мнимой величиной. Движение в этом случае имеет апериодический (непериодический) характер — система, выведенная из положения равновесия, возвращается в положение равновесия без колебаний. Какой из этих методов система приходит в равновесие, зависит от начальных условий.

Вынужденные вибрации. Резонанс

Вынужденные колебания — это те, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (силы воздействия). Пусть движущая сила изменяется со временем по гармоническому закону: f = F0 cos t, где F0 — амплитуда, круговая частота движущей силы.

При составлении уравнения движения необходимо учитывать, помимо движущей силы, также те силы, которые действуют в системе при свободных колебаниях, то есть квазиупругую силу и силу сопротивления среды.

Разделив это уравнение на m и переместив члены из dx и d2x в левую сторону, мы получим неравномерное линейное дифференциальное уравнение второго порядка:

где коэффициент ослабления, собственная частота системы.

Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты движущей силы к собственной частоте колеблющегося тела называется резонансом, колебания, возникающие в этом случае, являются резонансными, а их частота называется резонансным колебанием.

Автоколебания

Системы, которые автоматически регулируют подачу энергии от внешнего источника, называются автоколебательными, а происходящие в них непрерывные периодические процессы называются автоколебаниями. Такими системами являются часы, электрический звонок, ламповый генератор электромагнитных волн и т. Д.

Разложение колебаний в гармонический спектр. Использование гармонического анализа для обработки диагностических данных

Сложение гармонических колебаний, направленных вдоль одной прямой.

Есть случаи, когда тело вовлечено одновременно в несколько колебаний, происходящих вдоль одного и того же или вдоль разных направлений.

Рассмотрим сложение двух гармонических колебаний одного и того же направления, одинаковой частоты и с одинаковыми амплитудами, но с разными начальными фазами 01 и 02. Смещение x колеблющегося тела будет суммой смещений x1 и x2:

x = x1 + x2 = Acos (0t + 01) + Acos (0t + 02).

Используя формулу, известную из тригонометрии для суммы косинусов двух углов, имеем:

то есть получается гармоническое колебание той же частоты с начальной фазой и амплитудой Ares.

Как видно, амплитуда Ares результирующего колебания зависит от разности фаз добавленных колебаний.

Рассмотрим два крайних случая:

Колебания происходят в фазе, то есть 01 = 02, а затем и Ares = 2A.

Если амплитуды не равны, Arez = A1 + A2.

Колебания происходят в противофазе, то есть 01 = 02, затем. Следовательно, Ares = 0. Если амплитуды не равны, например, A1> A2, то Ares = A1 — A2.

Таким образом, при сложении двух одинаково направленных гармонических колебаний одного и того же периода и с одинаковыми амплитудами получается гармоническое колебание одного и того же периода с амплитудой, которое в зависимости от соотношения фаз добавленных колебаний может изменяться от двойного значение, если колебания происходят по фазе до нуля, если они находятся в противофазе.

При сложении гармонических колебаний с разными частотами результирующее колебание не будет гармоническим, а будет сложным.

Начальные колебания.
Результирующие колебания.

Комплексное колебание и его гармонический спектр

Согласно теореме Фурье любое сложное колебание может быть представлено как сумма простых (гармонических) колебаний (гармоник), периоды или частоты которых кратны основному периоду или частоте сложного колебания.

Множество простых колебаний, в которые можно разложить это сложное колебание, называется его гармоническим спектром.

В гармоническом спектре сложного колебания указаны частоты и амплитуды всех его простых колебаний. Обычно спектр представлен в виде графика, на горизонтальной оси которого нанесены частоты; затем для каждой из частот простых колебаний, имеющихся в спектре, создается ордината, соответствующая амплитуде этого колебания. Если гармонический спектр сложной вибрации содержит лишь небольшое количество простых колебаний, а его график состоит из отдельных ординат, то такой спектр называется линейчатым спектром.

Если спектр содержит простые колебания почти всех частот в определенных пределах, то он называется сплошным и его график строится в виде непрерывной огибающей кривой.

Установление гармонического спектра является основным методом анализа сложных колебаний. Этот анализ проводится с использованием специальных инструментов — анализаторов гармоник. Они также используются в медицине при исследовании, например, колебаний биопотенциалов головного мозга и т. д. Многие процессы человеческого организма носят периодический характер: сердечные сокращения, дыхание, наполнение кровеносных сосудов и т. Д.

Сложение взаимно перпендикулярных вибраций

В результате сложения двух взаимно перпендикулярных колебаний другого периода тело движется по сложным фигурам, форма которых зависит от соотношения периодов, амплитуд и начальных фаз добавленных колебаний и которые называются фигурами Лиссажу.

Механические волны, их виды и скорость распространения

Колебательная система может отдавать энергию во внутреннюю среду. Эта передача энергии становится возможной благодаря тому, что частицы самой среды представляют собой миниатюрные колебательные системы. Молекулы среды связаны между собой силами, законы которых в определенных границах подобны законам сил упругости. Если одна из частиц оказывается удаленной из положения равновесия, то силы, действующие на нее со стороны соседних частиц, заставляют ее снова вернуться в устойчивое положение. Однако, согласно закону равенства действия и реакции, соседние частицы также будут подвержены действию смещающих сил и, в свою очередь, будут удалены из стабильного положения. Таким образом, каждое возмущение, однажды возникшее в определенной части среды, будет постепенно распространяться, захватывая частицы все дальше и дальше от места начального возмущения.

Колебательный процесс, обусловленный взаимодействием частиц, будет распространяться в среде с определенной конечной скоростью. Процесс распространения колебаний в среде называется волновым движением или просто волной. Для нашего случая это будет упругая или механическая волна.

Различают продольные и поперечные волны. Форма распространяющихся в среде волн существенно зависит от упругих свойств среды.

Волна, распространяющаяся в том же направлении, в котором происходят колебания частиц среды, называется продольной волной.

Продольные волны генерируются в телах с объемной эластичностью, то есть противодействуют объемной деформации сжатия. Это характерно для всех тел, поэтому они образуются в любой среде: твердой, жидкой, газообразной. Продольные волны, в частности, включают в себя звук, инфразвук и ультразвук.

Волна, в которой колебательное движение перпендикулярно направлению распространения колебаний, называется поперечной.

Поперечные упругие волны образуются только в твердых телах, которые имеют упругую форму, то есть сдвиговые деформации (например, сейсмические волны в земной коре во время землетрясений; волны, движущиеся вдоль растянутой струны; крутильные волны, вызванные попеременно скручиванием и раскручиванием конца длинной стержень) противодействовать сдвиговым деформациям.

Продольные и поперечные колебания частиц среды, несущей волну, являются частными случаями волнового процесса. Существуют и другие волны, в которых колебательные движения состоят из одновременных продольных и поперечных смещений. Это набухающие волны, поверхность.

Волновое уравнение

Рассмотрим поперечную волну. В поперечной волне частицы среды не сдвигаются в направлении распространения волны. Но колебания каждой последующей частицы среды запаздывают по фазе относительно предыдущих частиц. В результате гребни и впадины волны, видимые глазу, движутся в направлении распространения волны. Это наблюдается наблюдателем как движение волны.

Под скоростью волны понимают скорость, с которой одинаковые фазы колебаний частиц движутся в среде. Эта скорость называется фазовой скоростью волны. Скорость волны зависит от упругих свойств (а также плотности) среды.

Расстояние между двумя ближайшими точками среды, колебания которых происходят в одной и той же фазе, называется длиной волны или расстоянием, на которое колебания в среде распространяются за время, равное одному периоду колебаний. Он численно равен произведению скорости V распространения волны на период T или отношению скорости распространения волны к частоте колебаний:

Поскольку скорость распространения волны зависит от свойств среды, длина волны при переходе волны из одной среды в другую изменяется, хотя частота колебаний остается неизменной.

Кроме того, при колебаниях A или T волна характеризуется формой колебаний частиц в волне. Как и вибрации, волны делятся на простые (гармонические) и сложные.

Колебания, возбужденные в одной точке в однородной изотропной среде, распространяются от нее равномерно во всех направлениях, такая волна называется сферической. Если источник колебаний имеет значительную плоскую поверхность, то волна от него будет распространяться в направленном потоке, перпендикулярном поверхности источника; такая волна называется плоскостью.

Составляем уравнение плоской гармонической волны, которое позволяет определить смещение S точки B среды на любом расстоянии x от начальной точки A в направлении распространения волны в любое время. Пусть для начальной точки A уравнение колебаний: SA = A стоимость.

Точка B колеблется с фазовой задержкой на угол 0 = t0, соответствующий временному интервалу t, в течение которого волна проходит расстояние x между точками A и B. Тогда для точки B уравнение колебаний будет иметь вид:

SB = A cos (t — 0) = A cos (t — t0) = A cos (t — t0)

Подставляя значение t0 =, где V — скорость распространения волны, получаем:

Заменив в уравнении V = и = 2, тогда:

Таким образом, смещение точек S среды в упругой волне является функцией двух переменных: времени t и расстояния x точки от центра возбуждения колебаний, то есть S = f1 (x, t) ,

Если выбрать определенный момент времени (t1 = const), то уравнение дает зависимость смещения от расстояния x: St = f2 (x), то есть величину смещений точек среды вдоль направление х в данный момент времени t1. График этой зависимости (как снимок волны) называется волновым графиком. Для простой (гармонической) волны график имеет форму синусоидальной волны или волны косинуса.

Связь между смещением S точки, ее координатой x и временем t, выраженная в дифференциальной форме, называется волновым уравнением.

Чтобы составить уравнение плоской волны, находим частные производные второго порядка смещения S по времени t и координате x:

Таким образом, вторая производная временного смещения пропорциональна второй производной координатного смещения. Коэффициент пропорциональности равен квадрату скорости распространения волны V. Это дифференциальное уравнение плоской волны, распространяющейся в направлении оси x со скоростью V (см. Формулу 17). Он в наиболее общем виде описывает распространение волнового процесса.

Основные характеристики (амплитуда, период или частота, длина волны и форма волны) продольной волны, ее уравнение и графика аналогичны поперечной.

Энергетические характеристики волны

Гармонический спектр механических колебаний

Во время движения волны происходит передача энергии, которая состоит из кинетической и потенциальной энергий вибрирующих частиц среды. Более того, потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне, нет взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения одной и другой энергии изменяются одновременно (по фазе) в соответствии с изменением смещения частиц.

Мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебаний, и в каждый момент времени эти значения для разных частиц различны. Однако среднее значение энергии за период колебаний для всех частиц одинаково и составляет.

Значение, численно равное средней энергии Esr, передаваемой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность и измеряется в единицах мощности — Вт.

Поток энергии на единицу поверхности называется плотностью потока энергии и измеряется в Вт / м2. Плотность потока энергии также называется интенсивностью волны.

Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.

Вектор, показывающий направление распространения волны и равный потоку энергии, проходящему через единичную область, перпендикулярную этому направлению, называется вектором Умова.

Вектор Умова для упругой волны зависит от плотности среды, квадрата амплитуды колебаний частицы, квадрата частоты колебаний и скорости распространения волны.

Николай Алексеевич Умов (1846–1915) — исследователь потока энергии. Идеи о движении энергии были изложены в его диссертации «Уравнения движения энергии в телах», которую он защищал в 1874 году на физико-математическом факультете Московского университета. И только спустя десять лет английский физик Пойнтинг пришел к тем же выводам о движении энергии. Имя Умова вошло в историю физики

Энергетические характеристики волны

Гармонический спектр механических колебаний

Из формулы следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебаний, и в каждый момент времени эти значения для разных частиц различны.

Заключение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

сама колебательная система
источник энергии
устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

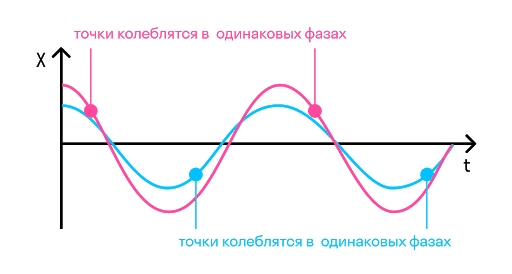
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

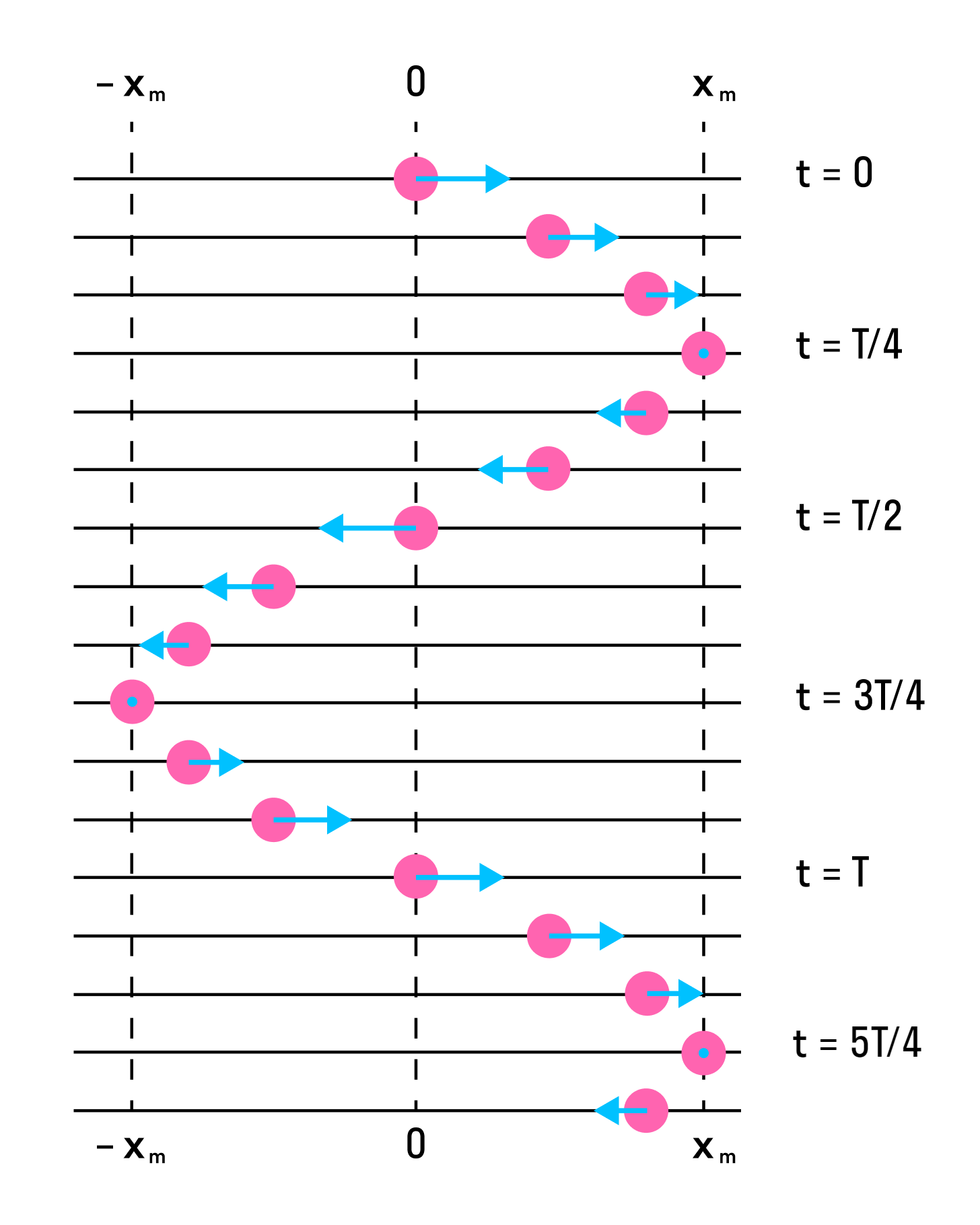
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

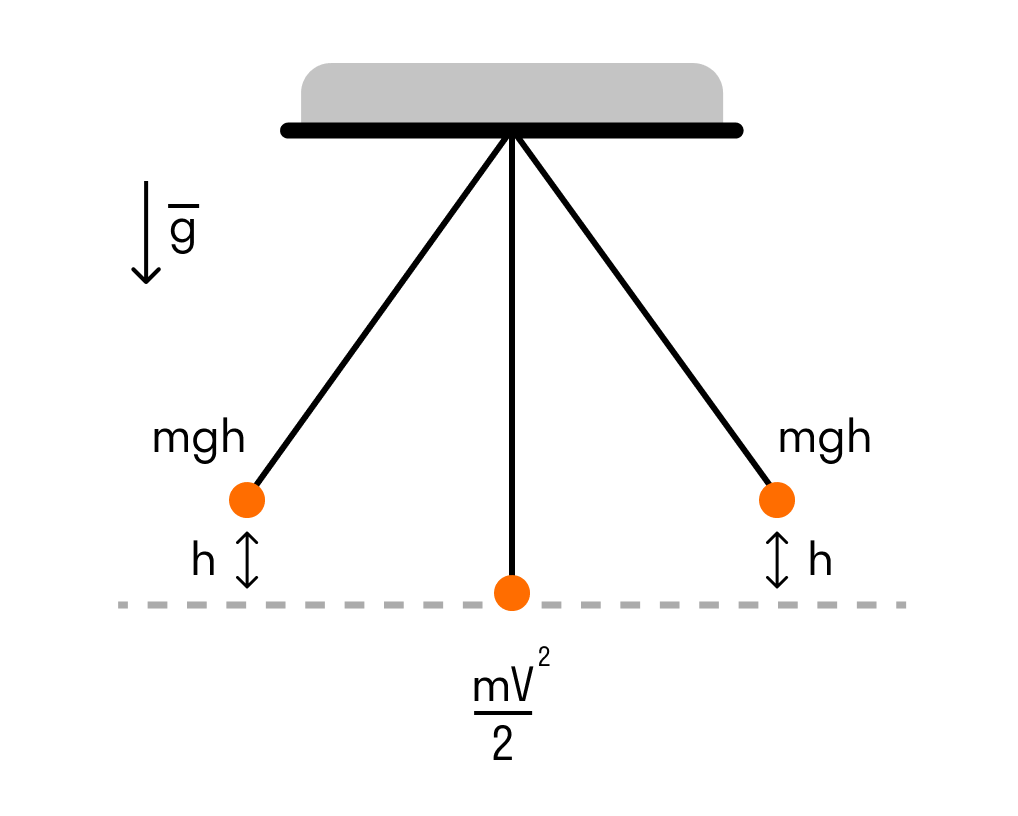
Рассмотрим его на примере математического маятника.

Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

источники:

http://natalibrilenova.ru/garmonicheskoe-kolebanie-uravnenie-avtokolebaniya-mehanicheskij-rezonans/

http://skysmart.ru/articles/physics/garmonicheskie-kolebaniya