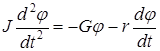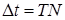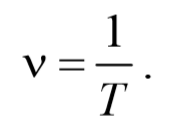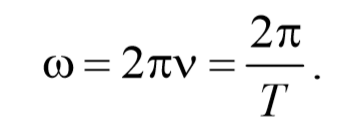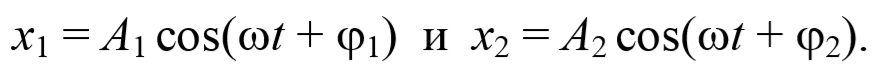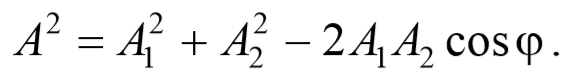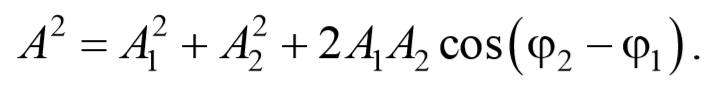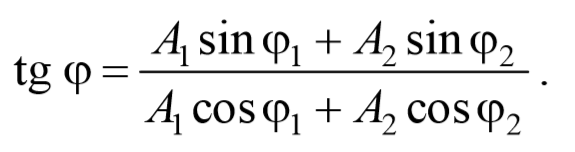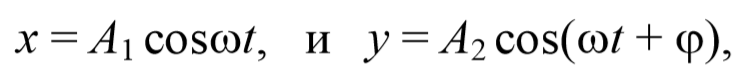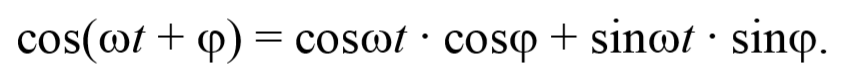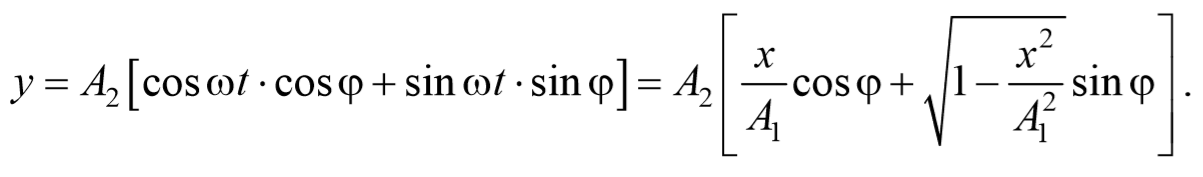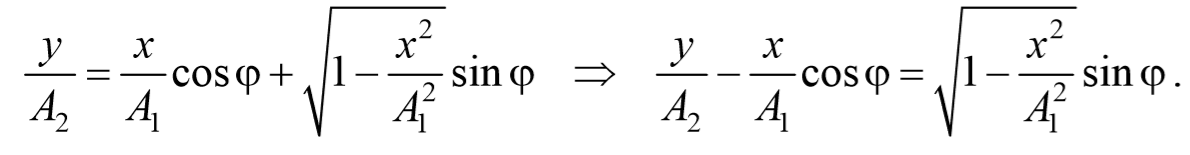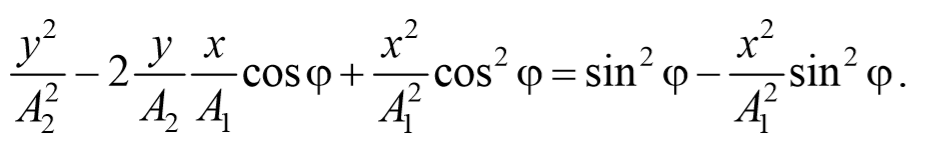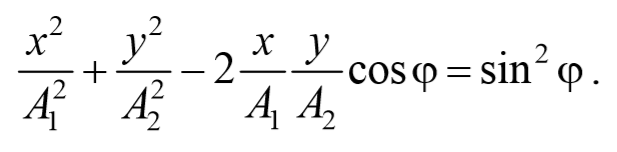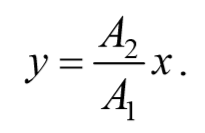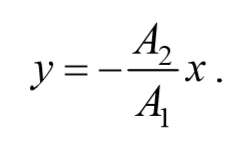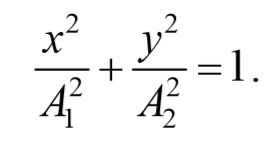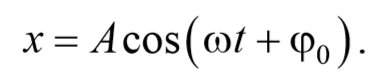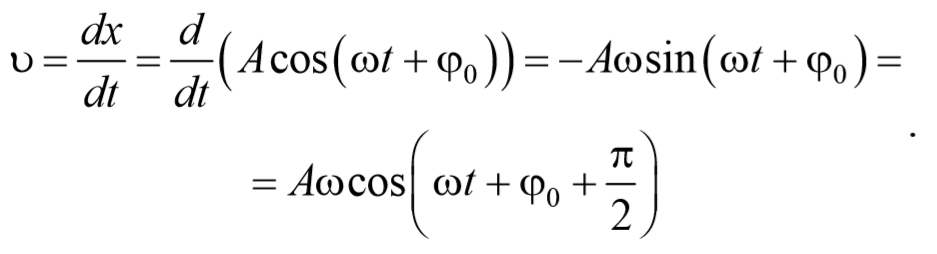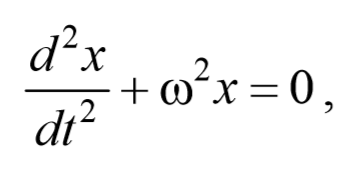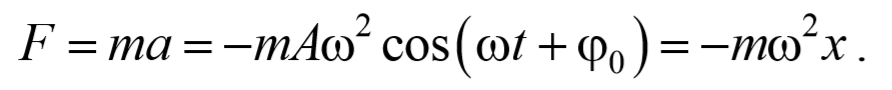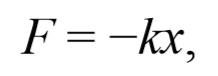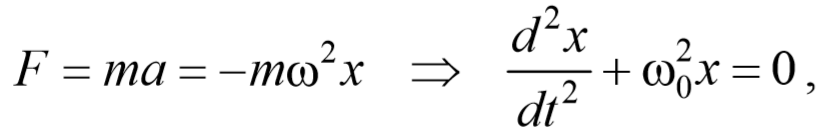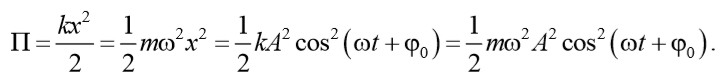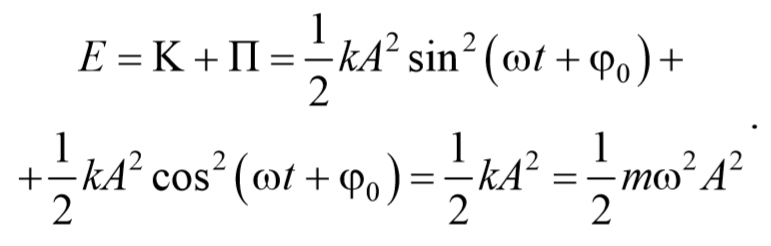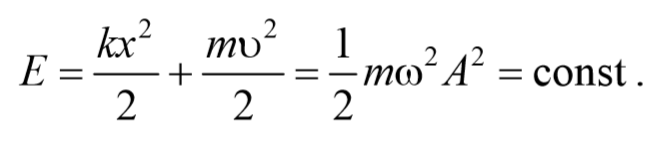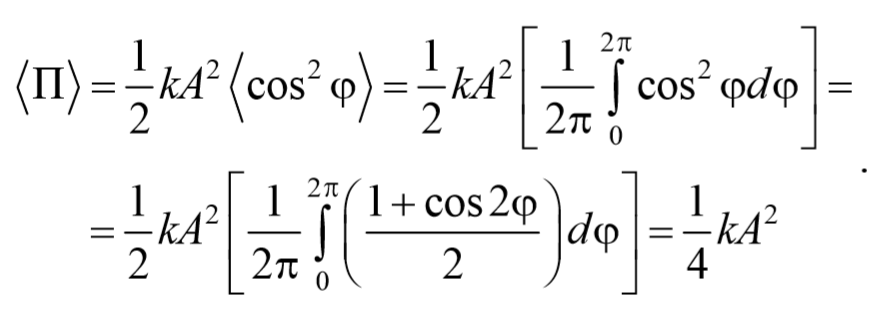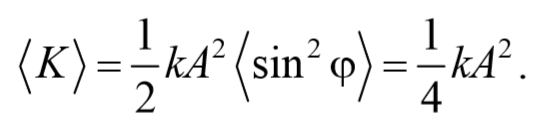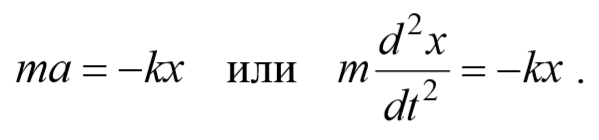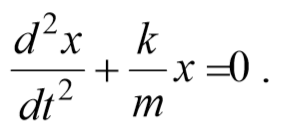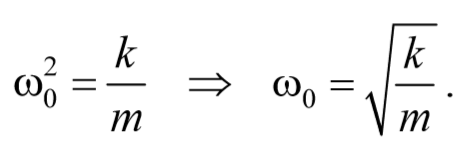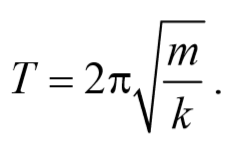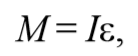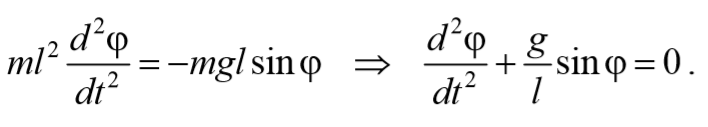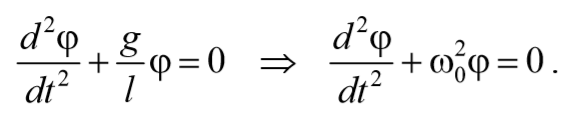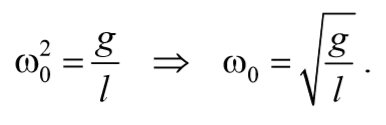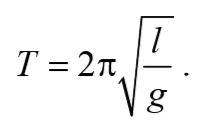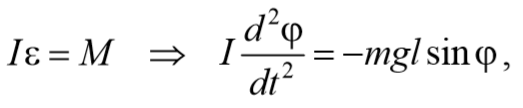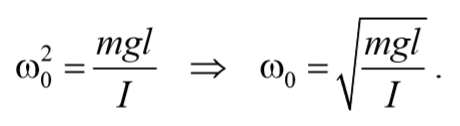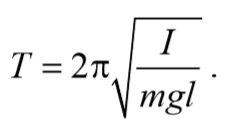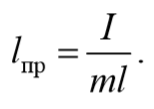II. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГООБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
З.Г.Морозова
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
к лабораторной работе по дисциплине «Физика»
Рекомендовано к изданию методическим советом
электротехнического факультета ФГБОУ ВПО «ВятГУ»
кандидат педагогических наук, доцент, кафедры «Прикладной математики и информатики» ФГБОУ ВПО «ВятГУ» Хохлова М.В.
| Изучение затухающих колебаний крутильного маятника и колебательного разряда конденсатора: учебно-методическое пособие к лабораторной работе по дисциплине «Физика» для студентов всех технических профилей подготовки, всех форм обучения / З.Г. Морозова. – Киров: Изд–во ВятГУ, 2015. –20с. |
© Морозова З.Г., 2015
© ФГБОУ ВПО «ВятГУ», 2015
Морозова Зоя Григорьевна.
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
к лабораторной работе по дисциплине «Физика»
Подписано в печать . Печать цифровая. Бумага для офисной техники.
Усл. печ. л. . Тираж 103 экз. Заказ .
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Вятский государственный университет»
610000, Киров, ул. Московская, 36, тел.: (8332) 64-23-56, http://vyatsu.ru
ЦЕЛЬ РАБОТЫ: изучить особенности возникающих в механических и электрических колебательных системах затухающих колебаний; измерение характеристик различных затухающих колебаний; выяснение влияния на них параметров колебательных систем.
I. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Затухающие колебания – это колебания, амплитуда которых из-за потерь энергии колебательной системы с течением времени уменьшается. Простейшим механизмом уменьшения амплитуды колебания является её превращение в теплоту вследствие; трения в механических колебательных системах, а также омических потерь и излучение электромагнитной энергии в электрических колебательных системах.
Уравнение затухающих колебаний определяется свойствами колебательных систем. Обычно рассматриваются линейные системы — идеализированные реальные системы, в которых параметры, определяющие их физические свойства, в ходе процесса не меняются. Линейными, например, являются математический маятник при малых амплитудах колебаний; колебательный контур, если его индуктивность и ёмкость не зависят ни от тока в контуре, ни от подаваемого напряжения.
Независимо от природы колебательного процесса дифференциальное уравнение затухающих колебаний линейной системы задается в виде:

где 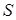


Решением уравнения (1) является функция:
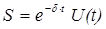
После нахождения первой и второй производных выражения (2) и подстановки их в уравнение (1) получим:

Решение уравнения (3) зависит от знака коэффициента при 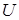
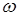

где 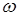

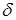
С учетом выражения (4) уравнение (3)запишется:

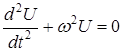
решением этого уравнения является функция вида

Следовательно, с учётом уравнений (2) и (5) решение уравнения (1) запишется:

где 
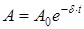
где 
График зависимости S(t) при затухающих колебаниях (6) приведена на рис. 1.
Затухающие колебания не являются периодическими, так как максимальное значение колеблющейся величины S1, достигнутое в некоторый момент времени t1 в последующем (при t > t1) никогда не повторится. Однако, при затухающих колебаниях величина S обращается в нуль, а также достигает максимальных значений через равные промежутки времени:

Величину Т обычно называют периодом (условным периодом) затухающих колебаний.
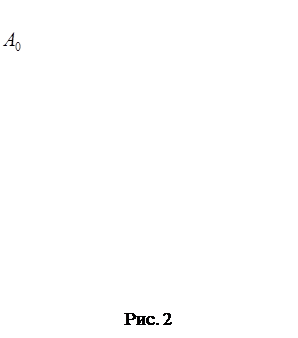

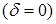
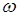
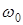
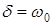

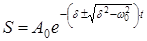
причём очевидно, что 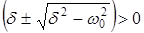
График апериодического движения приведен на рис. 2.
Время в течение, которого амплитуда затухающего колебания (7) уменьшается в 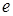
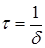


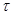
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний используется логарифмический декремент затухания.
Логарифмическим декрементом затухания называется безразмерная величина 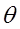
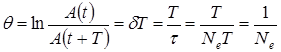
где 



Для характеристики изменения энергии колебательной системы используют понятие добротности 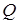
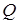
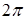




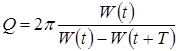
Так как 
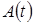
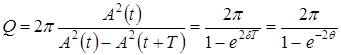
При условии малого затухания 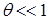
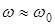

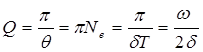
где Т= 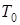




Полученные общие выводы можем применить для конкретных линейных систем.
В данной работе изучаются механические затухающие колебания на примере крутильного маятника и электромагнитные затухающие колебания на примере электрического колебательного контура.
II. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
В данной лабораторной работе механические колебания изучаются на примере крутильного маятника, представляющего собой массивное тело цилиндрической формы, подвешенное на упругой нити. Схема маятника изображена на рис. 3. Для торможения движения маятника используется трансформаторное масло, налитое в стакан С.



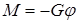
где 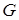
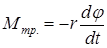
где 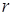

Если 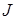

Введя обозначения 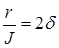
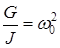

Уравнение (13) совпадает с уравнением (1) и, следовательно, крутильные колебания маятника будут происходить по закону затухающих колебаний (6).
Если за некоторое время 
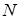
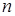
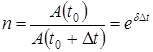
где 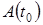

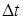
По определению время N колебаний равно
Логарифмический декремент затухания (6)c учетом (14) равен:
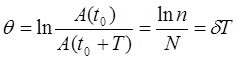
Добротность маятника 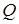

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.
Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид
1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.
2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.
3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .
За период система совершает одно полное колебание.
4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле
5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением
6) Фаза колебаний ωt + φ0 − фаза указывает местоположение колеблющейся точки в данный момент времени.
7) Начальная фаза φ0 − указывает местоположение колеблющейся точки в момент времени t = 0 .
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
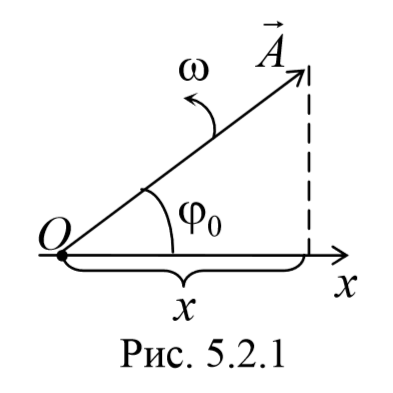
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ0 , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ0)
1. Сложение одинаково направленных гармонических колебаний.
Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x1 и x2 , которые запишутся следующим образом:
Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x2+x2 , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов
Так как угол между векторами А 1 и А 2 равен φ=π-(φ2-φ1) , то cos[π-(φ2-φ1)]=-cos(φ2-φ1) , следовательно, результирующая амплитуда колебания будет равна
Определим начальную фазу результирующего колебания.
Из рисунка видно, что начальная фаза результирующего колебания
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.
2. Сложение взаимно перпендикулярных гармонических колебаний.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид
где φ − разность фаз обоих колебаний.
Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$x\over A_1$$ , а sinωt= $$\sqrt<1-cos^2 ωt>=\sqrt<1-x^2\over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)
Перепишем это уравнение в следующем виде
После преобразования, получим
Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим
Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.
Рассмотрим несколько частных случаев и определим форму траектории для них:
a) разность фаз равна нулю [φ=0]
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= \sqrt
2) разность фаз равна ±π[φ=±π] .
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
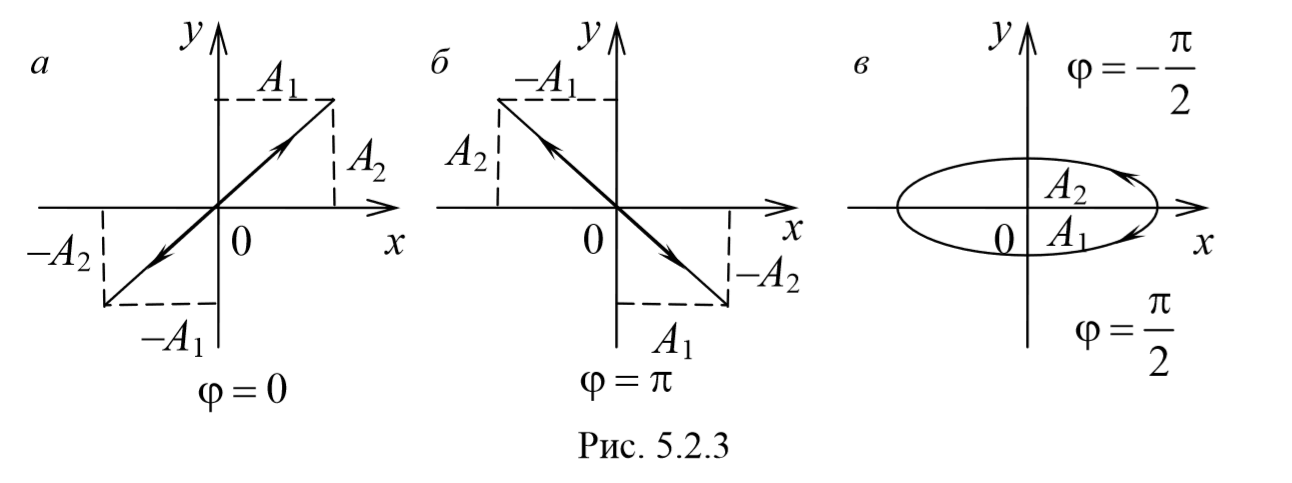
3) Разность фаз равна ± $$π\over 2$$ [φ=± $$π \over2$$ ] . Тогда
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$π\over 2$$ и φ=- $$π\over 2$$ отличаются направлением движения. Если φ=+ $$π\over 2$$ , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=-A2sinωt и движение совершается по часовой стрелке. Если φ=- $$π\over 2$$ , , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=A2sinωt и движение совершается против часовой стрелке.
Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.
На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.
По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
Продифференцируем по времени уравнение гармонических колебаний
и получим выражение для скорости
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .
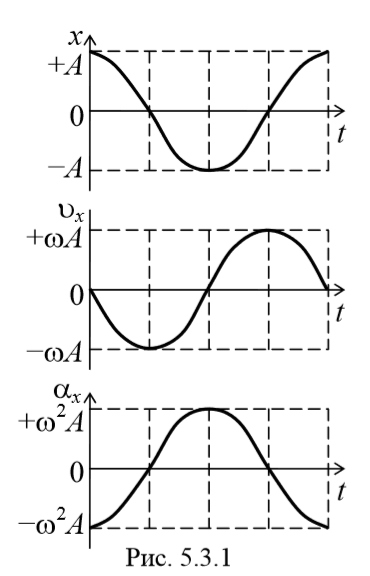
Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).
Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний
Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы
Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,
где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .
Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением
ω0 − собственная частота осциллятора.
Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ0) .
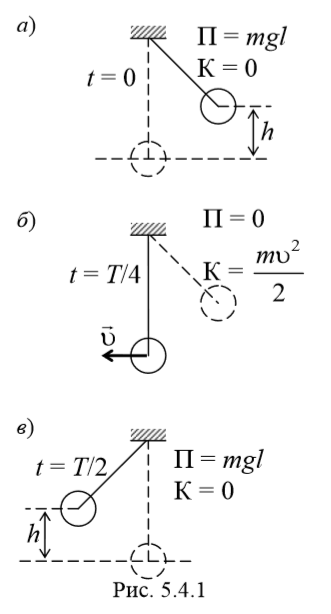
5.4. Энергия гармонических колебаний.
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
Кинетическая энергия тела, совершающего гармонические колебания равна
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
Следовательно, полная энергия гармонического колебания
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
Аналогично получается для среднего значение кинетической энергии
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2
5.5. Пружинный, математический и физический маятники.
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
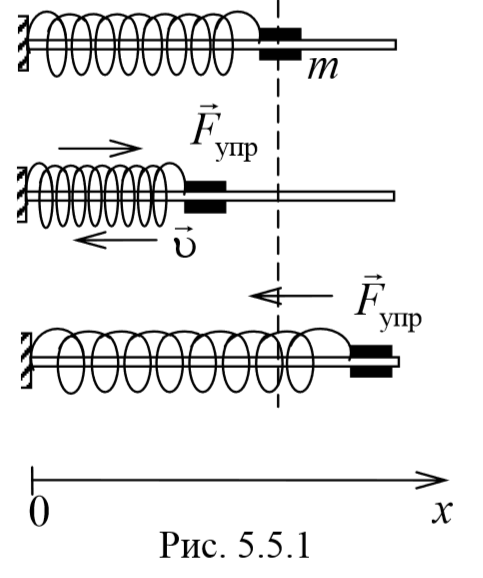
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox Fупр=ma . Упругая сила Fупр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
Так как период колебаний определяется по формуле T= $$2π\over ω_0$$ , то период колебаний пружинного маятника
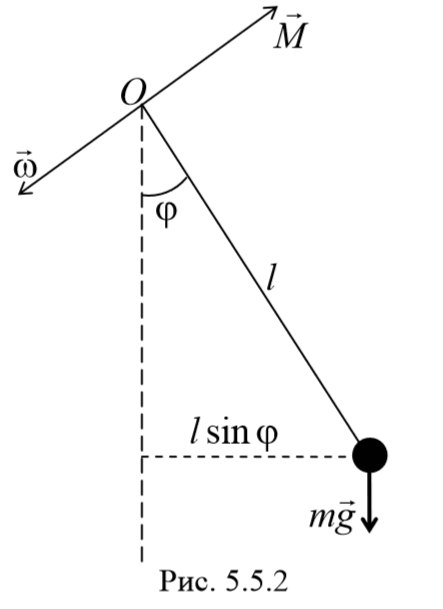
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.
При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения
где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φ\over dt^2$$ , получим
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
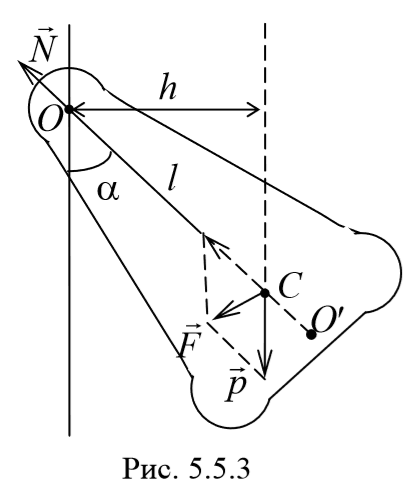
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .
Согласно основному уравнению динамики вращательного движения получаем
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$\sqrt
будет иметь такой же период колебаний, что и данный физический маятник.
Величина lпр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
МУ 4970: Определение моментов инерции тел методом крутильных колебаний
Лабораторная работа 1-20: Определение моментов инерции тел методом крутильных колебаний
Цель работы: изучение динамики вращательного движения твердых тел, знакомство с одним из методов определения моментов инерции тел – методом крутильных колебаний.
Приборы и принадлежности: унифилярный подвес ФПМ05, снабженный набором твердых тел (грузов) различной формы и электронным миллисекундомером.
Элементы теории
Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси имеет вид:
М – момент действующих на тело сил, взятый относительно оси вращения;
I – момент инерции тела относительно той же оси;
ϕ′′ – угловое ускорение тела.
Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы m точки и квадрата её расстояния r от оси:
Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных материальных точек (элементарных масс △mi ), на которые можно разбить тело:
В предельном случае, когда число элементарных масс стремится к бесконечности, сумма переходит в интеграл:
Как видно из определения, момент инерции тела есть величина аддитивная: момент инерции тела равен сумме моментов инерции его частей, а момент инерции системы равен сумме моментов инерции тел, входящих в систему.
Существуют различные способы экспериментального определения моментов инерции твердых тел. В данной работе используется метод вращательных (крутильных) колебаний.
Исследуемая система представляет собой твердое тело (например, брусок), подвешенное на струне, концы которой закреплены (рис. 1). После отклонения бруска на некоторый угол j от положения равновесия система начнет совершать крутильные колебания.
На основании формулы (1) уравнение движения бруска при малых углах отклонения ϕ примет вид:
I – момент инерции бруска относительно оси вращения;
r – коэффициент момента сил сопротивления;
k – коэффициент возвращающего (упругого) момента.
Коэффициент r численно равен моменту сил сопротивления при угловой скорости ϕ , равной 1 рад/с. А коэффициент k численно равен моменту упругих сил, возникающих при закручивании нити (струны) на угол, равный 1 рад.
Если сопротивление среды невелико, то первым членом правой части в уравнении (5) можно пренебречь и записать его в виде:
Обозначив kI = w 2 , окончательно получим дифференциальное уравнение гармонических колебаний:
Решение этого уравнения имеет вид:
ϕ0 – угловая амплитуда колебаний;
Как следует из приведенного решения (7), тело будет совершать гармонические колебания около положения равновесия. Циклическая частота w и период колебаний Т определяются величинами I и k по формулам:
Описание экспериментальной установки
Работа выполняется на установке – унифилярном подвесе ФПМ05, общий вид которого изображен на рис. 2.
Подвес представляет собой настольный прибор, на вертикальной стойке 1 которого размещены верхний и нижний кронштейны 2. Между кронштейнами 2 на стальной проволоке 3 подвешена рамка 4, предназначенная для установки и закрепления исследуемых тел 5, имеющих различные формы. В центрах граней грузов, в серединах их ребер и у вершин имеются углубления для закрепления в рамке.
На кронштейне 6 размещены: шкала 7, предназначенная для определения начального угла поворота рамки, электромагнит 8 для фиксации рамки в заданном положении и блок питания электромагнита 12. Электромагнит фиксируется в требуемом положении винтом 9.
На том же кронштейне 6 закреплен фотоэлектрический датчик 10. На основании 13 размещен миллисекундомер физический комбинированный 11, служащий для отсчета времени и числа колебаний.
В качестве исследуемых тел используются металлические грузы: цилиндр, параллелепипед и куб. Исследуемый груз закрепляется в рамке, начальное положение которой фиксируется электромагнитом. После отключения электромагнита (тумблер на блоке питания) рамка с грузом начинает совершать крутильные колебания.
Во время колебаний флажок, установленный на рамке, пересекает световой поток в щели фотоэлектрического датчика и сигнал, снимаемый с фотодиода, поступает на миллисекундомер.
Метод крутильных колебаний
Этот метод заключается в следующем. Тело с неизвестным моментом инерции I закрепляют в рамке подвеса. Период колебания такой системы будет равен
I0 – момент инерции ненагруженной рамки,
k – коэффициент упругости проволоки подвеса.
Согласно формуле (9) момент инерции I исследуемого тела можно вычислить, зная величины T, I0 и k. Период T колебаний несложно определить, измерив время t, за которое совершается N полных колебаний:
Для того, чтобы исключить неизвестные величины I0 и k, нужно измерить время t0 колебаний ненагруженной рамки, а также время tЭ колебаний рамки, нагруженной эталонным телом – телом с известным моментом инерции IЭ.
Таким образом, получаем систему уравнений:
Решая данную систему уравнений, получаем формулу для момента инерции выбранного нами тела:
Из выражения (12) следуют формулы для предельной относительной погрешности определяемого момента инерции:
△ t – погрешность измерения промежутка времени N полных колебаний рамки (предполагается, что эта погрешность одинакова для всех трех случаев измерения: t0, t и tэ).
Формулы (12) и (13) являются основными формулами для обработки результатов измерений, однако расчет существенно упрощается, если формулу (12) переписать в виде:
Если, кроме того, измеряемые промежутки времени t и tэразличаются незначительно, то малым по сравнению с единицей членом но пренебречь и представить (14) в виде:
Справедливость формулы (15) проверяется путем сравнения величины (t — tэ) (tэ+ t0 ) с относительной погрешностью результата EI, определяемой уравнением (13). Она справедлива, если:
Из уравнения (13) также следует, что чем больше полное время колебаний рамки, тем точнее получается результат. Поэтому в процессе прямых измерений рекомендуется измерять времена t0, t и tэдля
N = 50 колебаний рамки.
Задание
В задание входит определение моментов инерции двух тел различной формы относительно их центра масс теоретически и экспериментально.
Для теоретического расчёта моментов инерции по известным массам и размерам тел используются следующие выражения:
Iц и Iп — моменты инерции цилиндра и параллелепипеда соответственно;
R – радиус цилиндра;
a, b – размеры параллелепипеда.
Расчёт моментов инерции данных тел по экспериментально полученным данным производится по формулам (14) или (15). Необходимо также оценить абсолютные и относительные погрешности рассчитанных моментов инерции исследуемых грузов.
Порядок выполнения работы
Подготовка установки к работе
- Включите в сеть шнур питания миллисекундомера. Нажмите кнопку «СЕТЬ» на лицевой панели, при этом должны загореться цифровые индикаторы.
- После прогрева миллисекундомера (1–2 минуты) включите тумблер блока питания электромагнита.
- Ослабив стопорный винт электромагнита, установите его на угол, указанный преподавателем, в пределах 60-100º. Зафиксируйте электромагнит в этом положении тем же самым винтом.
- Поверните рамку так, чтобы металлический флажок, установленный на рамке, коснулся якоря электромагнита. При этом флажок притянется к якорю и рамка займет фиксированное положение.
- С помощью кнопок «СТОП» и «СБРОС» миллисекундомера обнулите счетчики числа и времени колебаний. Прибор готов к работе.
Проведение измерений
- Выключите тумблер блока питания электромагнита, при этом рамка начнет совершать колебательное движение и запустятся счетчики миллисекундомера. После N–1 полных колебаний рамки нажмите кнопку «СТОП» – отсчетное устройство, доработав до конца 50-го колебания, остановит счетчики. Запишите время t0– время 50-ти колебаний ненагруженной рамки. Число полных колебаний рамки может быть задано преподавателем дополнительно в пределах 30-60.
Остановив рукой колеблющуюся рамку, повторите операции, описанные в пп. 1.4, 1.5 и 2.1, еще два раза. Результаты измерений занесите в заранее подготовленную таблицу.
- Для закрепления исследуемого тела в рамке остановите рамку и освободите подвижную планку, отвернув гайки боковых цанг.
- Поднимите планку по направляющим и, придерживая её рукой, установите груз так, чтобы соответствующее углубление в центре одной из граней вошло в выступ на нижней перекладине рамки.
- Опустите подвижную планку по направляющим, затяните гайки боковых цанг и подожмите исследуемое тело винтом, находящимся на подвижной планке.
- Включите электромагнит и повторите операции, описанные в пп. 1.4, 1.5 и 2.1, три раза, результаты измерений занесите в таблицу.
- Для замены груза остановите рамку, отпустите гайки боковых цанг, переместите подвижную планку вверх и замените первый груз на второй, закрепив его в рамке, как указано в п. 2.4.
- Измерьте время 50-ти полных колебаний второго груза и эта- лонного тела по методике, описанной выше. В качестве эталонного тела можно использовать куб или цилиндр по указанию преподавателя. Результаты измерений занесите в таблицу.
- Измерьте размеры исследуемых тел простейшим измерительным прибором (штангенциркулем) и запишите эти значения, а также массу грузов в отчёт о лабораторной работе.
Порядок расчёта
- По выражениям (17), определяющим моменты инерции данных тел через массу и размеры, рассчитайте момент инерции эталонного тела (цилиндра или куба по указанию преподавателя). Оцените абсолютную погрешность по формулам:
R – радиус цилиндра;
a – сторона куба;
Jэц и Jэк моменты инерции цилиндра и куба, рассчитанные по выражениям (17);
△R и △a – систематическая погрешность измерений радиуса цилиндра и стороны куба соответственно.
- Рассчитайте относительную погрешность момента инерции эталонного тела.
- Используя данные таблицы, вычислите абсолютную и относительную погрешности измеренных промежутков времени t0 , t1 , t2 .
- По средним значениям промежутков времени N полных колебаний рамки с исследуемыми телами и без оцените относительные погрешности моментов инерции исследуемых тел по выражению (13).
Сравните последние с величиной |t — tэ| / (tэ+ t0 ) . Если неравенство (16) выполняется, то расчёт моментов инерции исследуемых грузов можно производить, применяя упрощённую формулу (15). В противном случае нужно использовать более точное выражение (14). Рассчитайте по соответствующим формулам моменты инерции исследуемых тел, а также абсолютные погрешности этих моментов инерции.
- По выражениям (17) вычислите теоретические моменты инерции исследуемых тел через массу и размеры. Оцените абсолютные по- грешности полученных значений моментов инерции по формулам (18) и (19), а также относительные погрешности.
- Сравните экспериментально полученные значения моментов инерции исследуемых тел с результатами расчётов по теоретическим формулам и сделайте соответствующие выводы.
Вопросы и задания для самоконтроля
- Сформулируйте основной закон динамики вращательного движения твердого тела.
- Дайте определение момента инерции твердого тела. Как его рассчитать теоретически?
- Получите дифференциальное уравнение крутильных колебаний, прокомментируйте его.
- Запишите уравнение колебательного движения крутильных колебаний. Чем определяется их период?
- Каковы прямые измерения в данной работе? В чем состоит роль эталонного тела?
Используя формулу (4), покажите, что моменты инерции цилиндра и прямоугольного параллелепипеда (рис. 3) относительно вертикальной оси их симметрии, проходящей через центр их масс, определяются выражениями (17).
Библиографический список
- Савельев И.В. Курс физики: учебник. 4-е изд. т. 1: Механика. Молекулярная физика. М.: Лань, 2008. 354 с.
- Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие для вузов. 8-е изд. М.: Академия, 2009. 720 с.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. 18-е изд. М.: Академия, 2010. 560 с.
Определение моментов инерции тел методом крутильных колебаний: методические указания к лабораторной работе / Рязан. гос. радио- техн. ун-т; cост.: М.А. Буробин, А.В. Брыков, Ю.В. Черкасова. Рязань, 2016. 8 с.
Представлена краткая теория крутильных колебаний, описан метод унифилярного подвеса. Приводятся порядок выполнения работы, методические указания по расчету погрешностей, контрольные вопросы и список рекомендуемой литературы.
Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 3. Библиогр.: 3 назв.
Вращательное движение твердого тела, момент инерции, крутильные колебания
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Определение моментов инерции тел методом крутильных колебаний Составители: Буробин Михаил Анатольевич
Брыков Александр Валериевич Черкасова Юлия Вадимовна
Редактор М.Е. Цветкова Корректор С.В. Макушина
Подписано в печать 15.02.16. Формат бумаги 60×84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
http://physics.belstu.by/mechanics_lk/mechanics_lk7.html
http://russianstuds.ru/opredelenie-momentov-inerczii-tel-2/