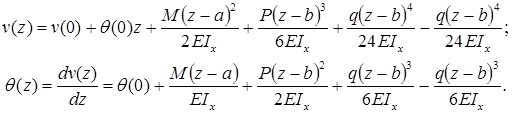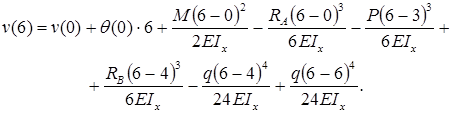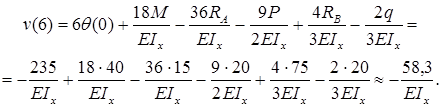Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

а после второго интегрирования – прогибы балки

.

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

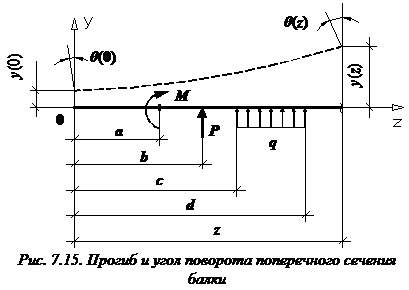
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

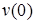
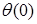
Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

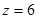
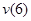
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .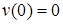

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

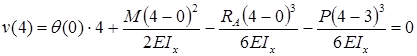
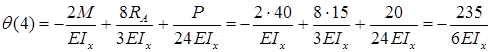
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

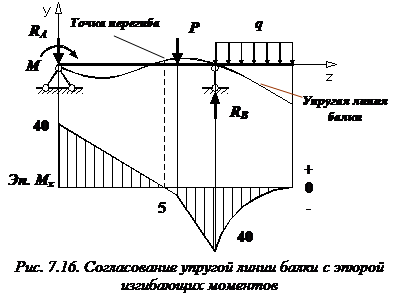
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Дифференциальное уравнение оси изогнутой балки, лежащей на сплошном упругом основании

Дифференциальное уравнение оси изогнутой балки, лежащей на сплошном упругом основании

• Дифференциальные уравнения оси Изогнутые балки, лежащие на твердом теле упругое основание В инженерной практике мы часто сталкиваемся с балками, которые находятся на сплошном упругом основании. Такими балками можно считать железнодорожные пути

шпалы на конвейерах 325фундаменты здания на основе грунта, фундамента плотины и др. Кроме того, такие балки также являются рельсовыми с бесконечно большим количеством опор,и расстояние между ними невелико по сравнению с длиной.

Расчет балки на упругом основании не может быть осуществлен с использованием Людмила Фирмаль

уравнений статики. Эта задача не определена статически. Уравнения статики позволяют найти только суммарную реакцию от основания, а не определить закон распределения реакций по длине пучка. Величина реакции в каждой точке зависит от отклонения луча, а отклонение луча зависит от реакции от основания. Для решения этой задачи обычно принимается гипотеза о величине реакции на

оседание основания. В качестве одной из наиболее распространенных гипотез, л л ь н о й з а б и с т и М ф д У Р Е К К И Й с К и й л ь н о й С К И Й с Л О В а н о й С К И Й с К и й Эта гипотеза о характеристиках почвы была впервые предложена акад. Н. И. сыр-бор из-1801 и его применение к балкам на упругом основании вел профессор Э. Он широко используется Винклер. В последнее время было выдвинуто

• несколько новых гипотез. Таким образом, одна из них состоит из двумерного упругого основания, отдельной пружины, соединенной нитью в неупругом горизонтальном положении у верхнего края, и ее концов так называемой упругой полупространственной гипотезы.И широко принят. Однако решение инженерных задач методами, основанными на этих гипотезах, все еще очень трудоемко. Рассмотрим расчет балки на основе упругости по гипотезе Фусса-

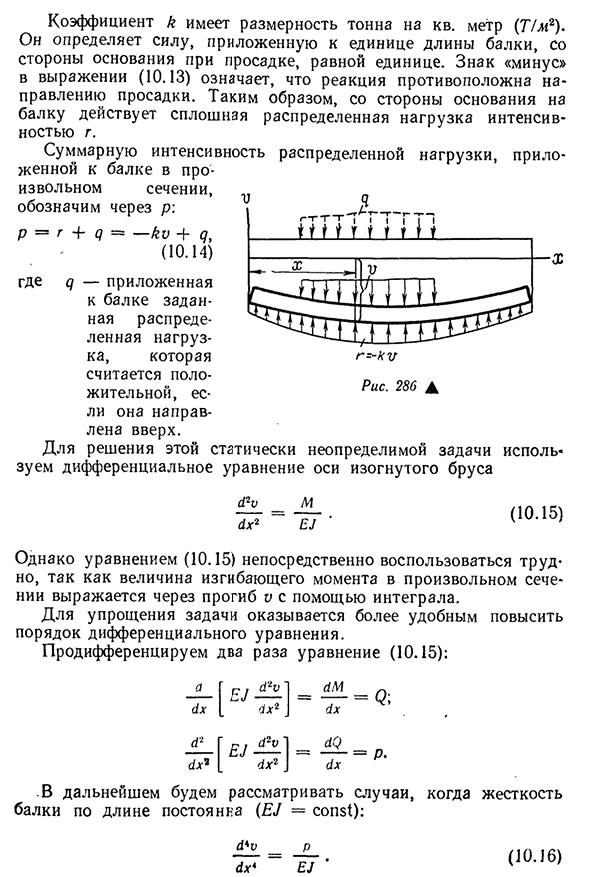
Винклера. Для риса. На рис. 286 показана картина деформации балки от внешней нагрузки, распределенной по любому конусу. Предполагается, что реакция от основания в каждой точке пропорциональна отклонению Г=-Ко(10.13) Куда? K=K\g-базовая реакция на единицу длины пучка, Т!M\V-просадка основания^, m\K ‘ — коэффициент пропорциональности, называемый

коэффициентом гибкости основания, или отношением ложа H/mg. Это соотношение Людмила Фирмаль

представляет собой сопротивление основания на 1 м2 в случае просадки, ширину балки B-кровати. В 326coefficient K имеет размеры тонн на квадратный метр(77м2). Он определяет силу, приложенную к единице длины балки от нижней части просадки равной единице. Знак минус (10.13)в выражении означает, что реакция противоположна направлению просадки. Таким образом, непрерывное распределение нагрузки g-интенсивности действует на балку со стороны основания. Общая сила распределительной

нагрузки, приложенной к балке в любом сечении, равна p: p=g4-d—Ki4-7, (10.14) Где d-распределительная нагрузка, приданная балке, и если она направлена вверх, то считается положительной. Для решения этой статически неопределенной задачи используются дифференциальные уравнения криволинейной оси пучка Сайт a2u (1х2 М Е > (10.15)) Однако величина изгибающего момента в любом поперечном сечении выражается через прогиб V с помощью интеграла, поэтому формулу (10.15) трудно использовать непосредственно. Для упрощения задачи удобнее увеличить порядок дифференциальных уравнений. Дифференциал по двойному

уравнению(10.15)): Но Да Е> с!2У а Х2 (И2 s1x* E1 y2u yh6 +4º4E /

0х‘ Или другие (EM’)™+4p4 (EM’)=9″. Когда мы думаем о»EM» =M、 а * м а*4-4≤4М=д». (10.20 утра)) Оба дифференциальных уравнения эквивалентны и могут быть использованы для решения практических задач.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института