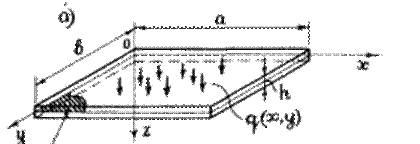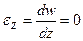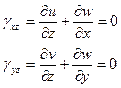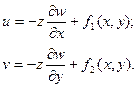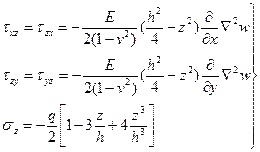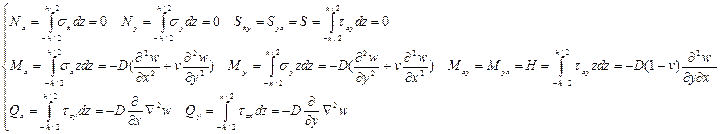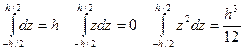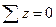Дифференциальное уравнение изогнутой срединной поверхности пластинки

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Изгиб прямоугольных пластинок. Дифференциальное уравнение изогнутой поверхности пластинки

Для расчета тонких пластинок с прямоугольной и трапециевидной формы более удобными оказываются декартовы координаты

Результатом использования гипотез Кирхгоффа в задаче изгиба пластинок в декартовой системе координат является:

— дифференциальное уравнение изогнутой поверхности:

, где: w = w (x,у) — функция прогиба, а — цилиндрическая жесткость.

Уравнение это называют уравнением Софи Жермен, оно представляет собою дифференциальное уравнение в частных производных четвертого порядка относительно функции w, зависящей от двух переменных (х и у). Общего решения этого уравнения, как и большинства других уравнений в частных производных, в математике неизвестно. Поэтому прямой метод решения, как это делается при решении обыкновенных дифференциальных уравнений, здесь оказывается невозможным, и приходится применять либо обратный метод (т. н. метод проб и ошибок) либо полуобратный метод, требующий всего одной попытки.

Наиболее универсальными, хотя и приближенными аналитическими методами расчета пластинок являются вариационные методы. Это метод Ритца-Тимошенко, метод Бубнова- Галеркина и метод Власова-Канторовича. Любой из них позволяет найти функцию прогиба w (x,у), удовлетворяющую как уравнению (1), так и конкретным граничным условиям на контуре пластинки. Все остальные параметры, в частности, усилия, напряжения, деформации и перемещения, определяются уже через найденную функцию прогиба. Приведем без вывода формулы внутренних усилий и напряжений в пластинке.

Усилия и напряжения в пластинках (пластинах). Внутренние усилия в сечениях пластинки:

— изгибающие моменты

— крутящие моменты

— поперечные силы

Соответственно шести усилиям в сечениях пластинки возникают и шесть составляющих напряжений:

— нормальные напряжения

— касательные напряжения, действующие параллельно срединной плоскости (с.п.) пластинки

— касательные напряжения, направленные перпендикулярно срединной плоскости пластинки

В формулах напряжений обозначено:

— момент инерции сечения шириной, равной 1 и высотой h (погонный момент инерции), z — расстояние от срединной плоскости пластинки до той точки, где определяется напряжение.

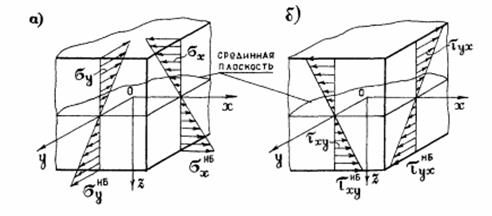
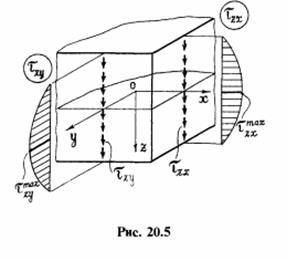
Покажем эпюры напряжений

Эпюры напряжений в прямоугольной пластинке при изгибе

Наибольших значений нормальные напряжения достигают в точках, расположенных у поверхностей пластинки, наиболее удаленных от срединной плоскости, при :, где

— погонный метр сопротивления, то есть момент сопротивления сечения единичной ширины.

Касательные напряжения, параллельные срединной плоскости, достигают наибольшей величины тоже в точках у поверхностей пластинки:

а касательные напряжения, направленные перпендикулярно срединной плоскости, наоборот, имеют максимум в точках срединной плоскости (при z=0):

Для сравнения — в балке при изгибе возникают всего две составляющие напряжений: это σ_х и τ_zx.

Гипотезы применяемы при расчете пластин

Основные понятия.

Пластинка – это призматическая или цилиндрическое тело высота (толщина) которого мала по сравнению с размерами в плане.

Срединнаяплоскость – плоскость, которая делит пластину пополам по толщине. При изгибе пластинки, срединная плоскость превращается в изогнутую срединную поверхность пластинки.

Линейныйэлемент – отрезок прямой, соединяющий внешние поверхности пластины перпендикулярно к срединной плоскости. Длина линейного элемента равна толщине пластины.

Контурпластинки – это линия пересечения боковой поверхности пластинки со срединной плоскостью.

В инженерной практике чаще всего встречаются прямоугольные и круглые пластинки (Рисунок.1.)

Рис.1. Прямоугольная (а) и круглая (б) пластинки

Условие закрепления пластинки:

· Закрепление по контур;

· Свободные края от закрепления;

Пластины могут быть постоянной и переменной толщины. В зависимости от соотношения между основными размерами пластины и её прогиба различают категории:

Толстые плиты – это пластины, у которых 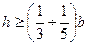, где b – минимальный размер в плане. Толстые плиты применяются в качестве фундаментов зданий, гидротехнических сооружений, опорных частей станков и машин. Расчет производится на основании уравнений пространственной задачи теории упругости;

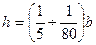
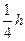
Тонкие пластины – пластины, у которых где b – наименьший размер в плане. Прогиб составляет не более . Тонкие пластинки применяются в строительстве в качестве железобетонных плит и панелей жилых и промышленных зданий, металлических настилов, днищ резервуаров;

Гибкие пластины – это пластины, у которых прогибы соизмеримы с толщиной. Гибкие пластины применяются в приборостроение и авиастроение. Расчет производится, учитывая геометрическую нелинейность. Изгиб пластины вызывается действием поперечных нагрузок перпендикулярных к срединной плоскости. Абсолютно гибкая пластина (мембрана) это пластина, у которой прогибы значительно превосходят толщину. Такие пластинки обладают малой жесткостью на изгиб и в основном работают на растяжение в срединной плоскости. При расчете гибких пластин учитывают работу на изгиб на растяжение и сжатие в срединной плоскости.

Жесткая пластина – это пластина, у которой прогибы малы по сравнению с толщиной. 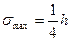. При расчете жестких пластин учитывается только работа на изгиб.

Гипотезы применяемы при расчете пластин

1) Гипотеза прямых нормалей.

Любой линейный элемент при изгибе остается прямым и перпендикулярным к срединной поверхности пластины после деформации. Исходя из этого следует что сдвиги в поперечных плоскостях отсутствуют. 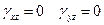.Длина линейного элемента не изменяется следовательно линейная деформация в направлении Z отсутствует:

2) Гипотеза о нерастежимости срединной плоскости

В срединной плоскости отсутствует деформация растяжения сжатия и сдвига следовательно срединная плоскость является нейтральной. 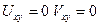. Давление между слоями отсутствует. Сигма=0

3)Гипотеза об отсутствии давления между слоями пластинки

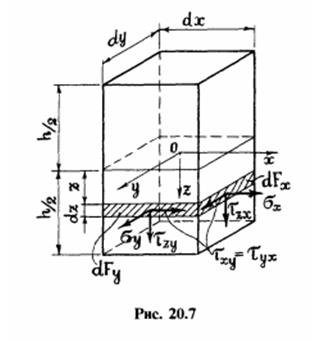
Перемещение и деформации в пластине при изгибе.

Рассмотрим изгиб пластинки под действием поперечной нагрузки. При соотношения Коши с учетом гипотез, получаем:

С учетом 2-й гипотезы, получаем:

Тогда перемещения равно:

(*)

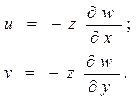
Линейное и угловое дифференцирование из формы Коши, равна:

(**)

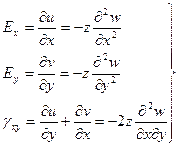
Напряжение в пластинах при изгибе

Из формул обобщенного закона Гука с учетом гипотез и формулы (**) получаем:

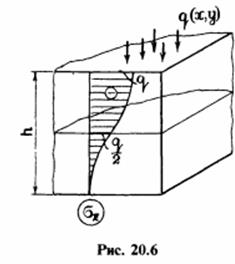
Полученное напряжение изменяется по толщине пластинки по линейному закону(Рисунок 2)

Усилия в пластинках. Дифференциальные уравнения изогнутой срединной поверхности пластинки (Уравнение Софьи Жермен)

Формула(***)Вписать в нее(20.7)(20.9)

Тогда внутренние силовые факторы (погонные усилия – изгибающие моменты и поперечные силы, крутящий момент) с учетом граничных условий и с учетом (***) в сечениях пластинки перпендикулярных к её срединной плоскости под действием поперечной нагрузки равны:

Где D(формула 20.11) цилиндрическая жесткость пластинки.

Граничные условия

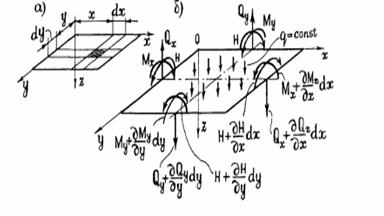
Под действием внешней нагрузки на гранях элемента пластинки возникают внутренние усилия (Рисунок.4.)(20.9)

Из условия равновесия выделенного элемента получаем

(20.15 первое уравнение)

Сумма моментов относительно X=0 есть (20.15 3 выражение)

Сумма моментов относительно Y=0 есть (20.15 2 выражение)

Подставим Б и С в А, ис учетом 4тогда получим дифференциальное уравнение изогнутой срединной поверхности пластинки (Уравнение Софьи Жермэн):

(Самуль 8.15 и 8.16 переписать)

Дата добавления: 2016-02-09 ; просмотров: 3222 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Дифференциальное уравнение изгиба пластинки

Пермский Государственный Технический Университет

Кафедра «Динамика и прочность машин»

СТРОИТЕЛЬНАЯ МЕХАНИКА

Изгиб пластин

Рецензенты: д-р техн. наук, директор ИМСС УрО РАН В.П. Матвиенко; канд. физ.-мат. Наук, проф. Кафедры ДПМ Пермского государственного технического университета А.А. Лежнева

Кузнецова Е.В., Колмогоров Г.Л.

К60 Изгиб пластин: Учебное пособие к решению задач и лабораторному практикуму по исследованию прогибов при нагружении квадратных и круглых пластин / Пермский государственный технический университет. Пермь, 2005. 32 с.

Рассматриваются понятия, определения и характеристики, используемые в теории пластин, приведены основные уравнения пластин, а также показано влияние граничных условий на результаты решения подобных задач. Теоретические положения иллюстрируются примерами.

Даны методические указания к лабораторным работам: определение прогибов при нагружении сосредоточенной силой квадратной пластинки; напряженно-деформированное состояние при изгибе круглой пластинки.

Пособие предназначено для студентов специальностей «Динамика и прочность машин», «Компьютерная механика», изучающих курс «Строительная механика».

Ó Пермский государственный

технический университет, 2005

ОБЩИЕ СВЕДЕНИЯ

Раздел «Теория пластин» входит в комплексную дисциплину «Строительная механика» специальности «Динамика и прочность машин».

Существует большое количество деталей конструкций, машин и механизмов с определенными характеристиками и свойствами, которые при моделировании и абстрагировании можно описать как пластины. Конструкции с использованием деталей подобных пластинам легкие, прочные и широко используются в строительстве, аэрокосмической технике, судо-, автомобиле-промышленности. Расчет пластин на прочность, жесткость и устойчивость – это задачи строительной механики.

Пластина – это модель формы, к которой можно отнести тела, у которых один габаритный размер (толщина) много меньше двух других (см. рис.1).

Рис. 1. Пластинка

Определяющими характеристиками для пластин являются (рис.1): срединная поверхность – плоскость равноудаленная от наружных поверхностей, а также толщина h и величина прогиба w при действии нагрузки P.

В зависимости от величины прогиба пластинки подразделяют на:

1) жесткие пластины, где величина прогибов не превышает 20-25% от толщины пластинки преобладают изгибные напряжения, а зависимость между прогибами и нагрузкой линейна;

2) гибкие пластины, с прогибами в которых возникают цепные (мембранные) напряжения, действующие в плоскости срединной плоскости.

3) абсолютно гибкие пластинки, в которых прогиб при действии нагрузки в 5-6 раз больше толщины зависимость между прогибами и нагрузкой нелинейна, преобладают мембранные напряжения, а изгибными напряжениями можно пренебречь.

В тех случаях, когда прогибы малы в сравнении с ее толщиной, то есть речь идет о жестких пластинах, можно построить удовлетворительную приближенную теорию изгиба под поперечными нагрузками, основываясь на следующих допущениях:

1. В срединной плоскости пластинка не испытывает никаких деформаций. При изгибе эта плоскость остается нейтральной.

2. Точки пластинки, лежащие до загружения на нормали к срединной плоскости, остаются в процессе изгиба на нормали к ее срединной поверхности. Это допущение эквивалентно пренебрежению влиянием перерезывающих сил на прогиб пластинок, что допустимо, за исключением случая пластины с отверстием, когда перерезывающие силы имеют большое значение.

3. Нормальными напряжениями в направлении, поперечном к срединной плоскости пластинки, допустимо пренебрегать ( ).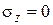

Основываясь на этих допущениях можно все компоненты напряжений выразить через прогибы пластинки.

Цилиндрическая жесткость.

Дифференциальное уравнение изгиба пластинки

Рассмотрим задачу об изгибе длиной прямоугольной пластинки, толщиной h, несущей поперечную, не изменяющуюся по длине пластинки нагрузку Р(х). Изогнутую поверхность участка такой пластинки, достаточно удаленного от ее концов, можно при этом считать цилиндрической, с осью цилиндра, параллельной пластинки (рис. 2).

Для вывода дифференциального уравнения изгиба выделим элементарную полоску как стержень прямоугольного поперечного сечении пролетом l, толщиной h. При вычислении обусловленных изгибом напряжений в таком стержне мы предполагаем, что поперечные сечения стержня остаются плоскими, испытывая лишь повороты относительно своих нейтральных осей. Если в концевых сечениях стержня не приложено никаких нормальных сил, то нейтральная поверхность стержня совпадает со срединной поверхностью пластинки, и относительное удлинение волокна, параллельного оси х, окажется пропорциональным его расстоянию от срединной поверхности. Кривизну изогнутой оси стержня можно будет при этом принять равной . Относительное удлинение волокна, отстоящего на расстоянии от срединной поверхности (рис.3) будет иметь вид

.

Пользуясь законом Гука, выразим относительные удлинения и заштрихованного на рис.3,а элемента в функции действующих на него нормальных напряжений. Для достаточно длинной пластины ( ) реализуется схема плоского напряженного состояния (ПНС) . С учетом обобщенного закона Гука

,

, (1)

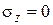
где – коэффициент Пуассона.

Для того, чтобы пластинка сохранила при деформации непрерывность, необходимо, чтобы поперечная деформация ее в направлении у была равна нулю. Второе из уравнений (1) даст нам .Подставив это значение в первое, получим

, (2)

где – относительное удлинение волокна, отстоящего на расстоянии от серединной поверхности, которое имеет вид

Располагая выражением для напряжения изгиба , находим посредством интегрирования изгибающий момент в элементарной полоске

. (3)

Вводя обозначения , (4)

представим уравнение изогнутой кривой, т.е. кривой прогибов, для элементарной полоски в следующем виде:

, (5)

Здесь величина D играет ту же роль, что и произведение El, входящее в формулы изгиба балки, называется цилиндрической жесткостью пластины при изгибе.