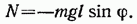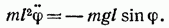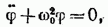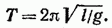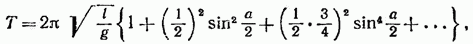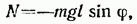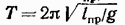Дифференциальное уравнение колебаний моста имеет вид

Дифференциальные уравнения, описывающие колебания моста

Разрешающие дифференциальные уравнения колебаний моста, представленного конечно-элементной моделью, преобразуются к совокупности n типовых обыкновенных дифференциальных уравнений второго порядка /11-12/ относительно обобщённых координат :

, (6.2)

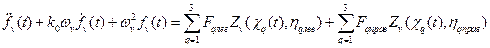
где 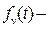неизвестная функция времени, отвечающая v-й собственной форме колебаний моста; n – число удерживаемых собственных форм; , – координаты в поперечном направлении точек опирания ой оси по левой и правой сторонам трёхосного автомобиля; ординаты собственных форм.

Прогибы ортотропной плиты проезжей части под ой осью по левой и правой сторонам трёхосного автомобиля отражают влияние обратной связи в совместных колебаниях системы «автомобиль– мост» и определяются по следующим формулам:

(6.3)

В качестве инертной подвижной нагрузки принят трёхосный самосвал SHACMAN полной массой M=41,0т. При вычислении квазистатической составляющей реакции главных балок пролётного строения на проезд трёхосной подвижной нагрузки использовалось прямое интегрирование уравнений движения с помощью численной пошаговой процедуры методом Ньюмарка. При этом решении подрессоренный автомобиль рассматривался только как силовое воздействие.

Для получения динамической составляющей реакции главных балок от совместного взаимодействия движущегося автомобиля с конструкцией моста, выполнялось совместное решение дифференциальных уравнений для автотранспортного средства (6.1) и для несущей мостовой конструкции (6.2) в программном комплексе Mathcad с использованием встроенной функции, реализующей метод Рунге-Кутта с постоянным шагом интегрирования. Шаг дискретизации по времени 0,005с. Скорость движения трёхосного грузовика принимается постоянной v=16 м/с = 57,6 км/ч. Время движения автомобиля 10,25с. Начальные условия для автомобиля принимаются статическими, для несущих конструкций моста – нулевыми. В расчёте грузовой автомобиль заезжает на разрезное пролётное строение моста начиная с 0,0 с. Изучение колебаний разрезного пролётного строения продолжается и после съезда автомобиля с моста. За время в 3,016с грузовик со скоростью 16 м/с полностью съедет с пролётного строения длиной 43,1м. В расчетах удерживалось из приведенных в табл. 6.1 настоящего раздела отчета пять собственных форм колебаний разрезного пролётного строения моста, наиболее значимые из которых первая изгибная и вторая изгибно-крутильная собственные формы.

Демпфирование для металлического разрезного пролётного строения задавалось постоянным для всех удерживаемых в расчёте собственных форм колебаний. Логарифмический декремент для рассматриваемого металлического пролётного строения моста – δ = 0,06. Параметр затухания колебаний – . Коэффициент затухания колебаний – .

Пробные вычисления динамической реакции моста на проезд автомобиля по абсолютно гладкой и не имеющей неровностей проезжей части показал, что колебания моста практически не возбуждаются. Это приводит к выводу, что влияние изменчивости прогибов (так называемой «обратной» связи), на колебания движущегося автомобиля и на колебания пролетного строения незначительно. Поэтому близкие к имеющим место при натурных динамических испытаниях колебания моста могут быть объяснены влиянием неровностей на проезжей части. Поэтому продолжим расчетное моделирование совместных колебаний моста после учета в разрешающих уравнений автомобиля кинематических возмущений от неровностей на проезжей части.

Рис. 6.24. Схематичное изображение положения проезда подвижной инертной нагрузки

Одиночную неровность в месте стыка соседних разрезных пролётных строений задаём детерминированной функцией в виде впадины. При проезде самосвалов через деформационные швы при натурных динамических испытаниях было зафиксировано, что возникают колебания кузова на частоте около 2,0 Гц. С целью моделирования этого процесса математически, впадину в месте деформационного шва необходимо сделать достаточно широкой, чтобы возбудились колебания кузова. При коротких одиночных неровностях и высоких скоростях движения грузовых автомобилей, колебания кузова не успевают возбудиться. Серия пробных расчётов показала, что ширину одиночной впадины в месте стыка пролётных строений необходимо сделать около 2,0м. Глубина впадины около 30мм.

Рис. 6.25. Расчетная одиночная неровность в начале пролётного строения в виде впадины шириной 2,0м и глубиной 30мм

Рис. 6.26. Расчётные вертикальныеколебания главных балок Б1 и Б2 в середине пролёта при проезде по рассматриваемому металлическому пролётному строению одиночного самосвала SHACMAN

Рис. 6.27. Расчётные спектральные плотности амплитуд вертикальных колебаний при проезде по рассматриваемому металлическому пролётному строению одиночного самосвала SHACMAN

Результаты моделирования совместных колебаний пролетного строения моста и движущегося через одиночную гладкую неровность трехосного автомобиля представлены на рис. 6.26, где изображены графики изменения прогибов главных металлических балок Б1 и Б2 в середине пролета №1 расчетной длиной 42,5м.

Из сопоставления приведенных на рис. 6.26 графиков с полученными при натурных испытаниях моста через реку Хопер и приведенных выше на рис. 6.19, видно, что характер колебаний и амплитудные значения близки. Совпадают также приведенные на рис. 6.20 и 6.27 спектральные плотности экспериментальных и расчетных графиков реакции моста на проезд трехосного автомобиля. Это дает основание считать, что принятые для расчетного моделирования предпосылки отвечают действительным особенностям рассматриваемых колебаний.

Дифференциальные уравнения колебаний

— гармонические,

— затухающие,

— вынужденные.

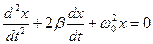
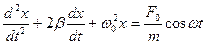
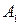
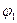
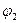
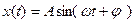
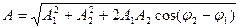
· Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых и , а начальные фазы и ,

, где

—

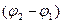
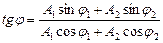
амплитуда результирующего колебания, — разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой

.

· Уравнение траектории точки, участвующей в двух взаимно­ перпенди­кулярных колебаниях с одинаковыми частотами

:

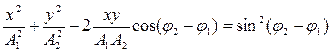
а) если 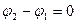, то — уравнение прямой,

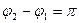
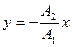
б) если , то — уравнение прямой,

в) если 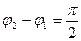, то — уравнение эллипса, приведённого к осям,

г) если и , то — уравнение окружности, где — радиус окружности.

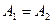
МЕХАНИЧЕСКИЕ ВОЛНЫ

· Длина волны, т.е расстояние между ближайшими частицами, колеблющимися в одинаковой фазе

,

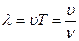
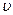
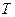
где — скорость волны, — период, — частота.

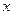
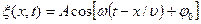
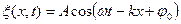
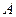
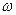
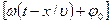
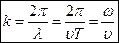
· Уравнение бегущей волны, распространяющейся вдоль положительного направления оси в среде, не поглощающей энергию,

или

, где

— амплитуда волны, — циклическая частота, -фаза волны, — начальная фаза, — волновое число.

Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Волна называется поперечной, если частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.

Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела. Продольные волны могут распространяться как в твердых телах, так и в жидких и газообразных средах.

Маятник

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.

Отклонение маятника от положения равновесия будем характеризовать углом образованным нитью с вертикалью (рис. 54.1). При отклонении маятника от положения равновесия возникает вращательный момент N, равный по величине — масса, a l — длина маятника). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписывать противоположные знаки 1). Следовательно, выражение для вращательного момента имеет вид

Напишем для маятника уравнение динамики вращательного движения. Обозначив угловое ускорение через и учитывая, что момент инерции маятника равен получаем:

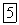
Последнее уравнение можно привести к виду

(54.2)

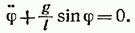
Ограничимся рассмотрением малых колебаний. В этом случае можно положить Введя, кроме того, обозначение

придем к уравнению

к зторое идентично с уравнением (53.1). Его решение имеет вид

Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону.

Как следует из (54.3), частота колебаний математического маятника зависит только от длины маятника и от ускорения силы тяжести и не зависит от массы маятника. По формуле (53.8) с учетом (54.3) получается известное из школьного курса выражение для периода колебаний математического маятника:

Отметим, что, решив уравнение (54.2), можно найти для периода колебаний следующую формулу:

где а — амплитуда колебаний, т. е. наибольший угол, на который отклоняется маятник из положения равновесия.

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m — масса маятника, а l — расстояние между точкой подвеса О и центром масс С маятника (рис. 54.2). Знак «—» имеет то же значение, что и в случае формулы (54.1).

Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать:

В случае малых колебаний (54.8) переходит в уже известное нам уравнение:

Через обозначена в данном случае следующая величина:

(54.10)

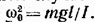
Из уравнений (54.9) и (54.10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника. В соответствии с (54.10) период колебаний физического маятника определяется выражением

(54.11)

Из сопоставления формул (54.6) и (54.11) получается, что математический маятник с длиной

(54.12)

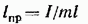
будет иметь такой период колебаний, как и данный физический маятник. Величину (54.12) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника — это длина такого математического маятника, период колебании которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.точку О на рис. 54.2).

Можно показать (рекомендуем это сделать в порядке упражнения), что при подвешивании маятника в центре качания О приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится нозым центром качания.

На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно Измерив период колебаний маятника и зная можно по формуле

найти ускорение свободного падения .

Уравнение колебаний

Определение и уравнение вибрации

Колебательные движения (или колебания) в физике и технике называют такими типами движений (или изменениями состояния), которые имеют некоторую степень повторяемости.

Колебания, которые происходят по законам синуса или косинуса, называются гармоническими.

Уравнение гармонических колебаний:

где t — время; x-значение, изменяющееся со временем (координата, заряд, ток, EMF и т. д.); A — амплитуда колебаний — максимальное отклонение осциллирующей величины от среднего (нулевого) значения; — фаза колебаний; — начальная фаза; w — циклическая частота (изменение фазы за единицу времени). За период фаза изменяется на

Дифференциальное уравнение гармонических колебаний

дифференциальное уравнение гармонических колебаний.

Типы периодических колебаний могут быть с любой степенью точности представлены в виде суммы гармонических колебаний, так называемых гармонических рядов.

Колебания, которые тело будет выполнять, если они выведены из равновесия (независимо от того, как) и оставлены сами по себе, называются свободными (собственными) вибрациями. Если собственные колебания обусловлены наличием только квазиупругой силы, то они будут гармоническими.

Колебания тела, вызванные одновременным воздействием квазиупругой силы и силы трения (которая пропорциональна мгновенной скорости: , называются затухающими колебаниями.

Уравнение (3) называется дифференциальным затухающим уравнением. Здесь — коэффициент затухания.

Решение дифференциального уравнения колебаний

Решением дифференциального уравнения затухающих колебаний (3) является отношение вида:

Уравнение (4) называется уравнением затухающего колебания. В уравнении (4) видно, что амплитуда затухающих колебаний зависит от времени. Константы А и определяются начальными условиями. Амплитуда колебаний уменьшается, и они обычно выглядят так, как показано на рис.

Период затухающих колебаний рассчитывается по формуле (5):

Коэффициент физического ослабления означает, что коэффициент затухания является обратной величиной времени релаксации. Время релаксации — время, в течение которого амплитуда уменьшается в е. Однако коэффициент затухания не полностью характеризует затухание. Демпфирование вибрации обычно характеризуется декрементом демпфирования. Последнее показывает, сколько раз амплитуда колебаний уменьшается за время, равное периоду колебаний. То есть декремент затухания определяется как:

Логарифм декремента затухания называется логарифмическим декрементом; он, очевидно, равен:

Если колебательная система подвергается внешней периодической силе, то возникают так называемые вынужденные колебания, имеющие не затухающий характер.

Принудительные вибрации следует отличать от автоколебаний. В случае автоколебаний в системе предполагается специальный механизм, который со временем со своими колебаниями «подает» небольшую часть энергии в систему.

Примеры решения проблем

Найти энергию свободных колебаний нагрузки, подвешенной на пружине. Рассмотрим случай физического маятника, зная, что жесткость пружины равна k, амплитуда колебаний A.

Найдем энергию свободных колебаний. Он представлен двумя типами энергии: кинетическими и потенциальными. Для пружинного подвесного шара:

Шаровые колебания описывают уравнение колебаний:

мы напишем уравнение скорости шара, зная, что движение происходит только вдоль оси X, поэтому:

Подставляя (1.2) и (1.3) в (1.1), получаем:

зная, что для физического маятника

Энергия свободных колебаний пропорциональна квадрату амплитуды колебаний

Одно колебательное движение выполняется вдоль оси X, другое — вдоль оси Y. Колебания гармоничны.

1) Частоты и фазы колебаний одинаковы, а амплитуды различны.

2) Частоты колебаний одинаковы, амплитуды различны. Фазы, складывающиеся колебания отличаются друг от друга на .

Определите, каковы траектории результирующих движений, если эти колебания складываются?

Запишем уравнения колебаний для каждого движения:

Чтобы найти траекторию результирующего движения, нам нужно исключить время из уравнений (2.1), (2.2). Для этого достаточно разделить по одному одно уравнение на другое, в результате получим:

Уравнение (2.3.) Показывает, что в этом случае добавление колебаний приводит к колебаниям по прямой, касательная которых определяется отношением амплитуд.

2. Пусть фазы добавленных колебаний отличаются друг от друга , то уравнения имеют вид:

Чтобы найти траекторию результирующего движения, исключив время, нам нужно квадратировать уравнения (2.3) и (2.4), сначала разделяя их на A1 и A2 соответственно, а затем складывая их. Уравнение траектории принимает вид:

Это уравнение эллипса. Для любых начальных фаз и любых амплитуд двух смещающихся взаимно перпендикулярных колебаний той же частоты результирующее колебание будет эллиптическим. Его ориентация будет зависеть от фаз и амплитуд добавленных колебаний.

1) В этом случае добавление колебаний приводит к тому, что колебания происходят по прямой, наклон которой равен

2) Траектория результирующего движения является эллипсом.