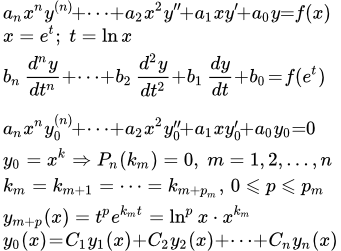Дифференциальное уравнение модифицированным методом эйлера

Метод Эйлера модифицированный.

Для уменьшения погрешности вычислений часто используется модифицированный метод Эйлера. Этот метод имеет так же следующие названия: метод Эйлера-Коши или метод Рунге-Кутта второго порядка точности.

Пусть дано дифференциальное уравнение первого порядка

с начальным условием:

Выберем шаг h и введём обозначения:

y_i — значение интегральной функции в узлах.

При использовании модифицированного метода Эйлера шаг h делится на два отрезка.

Иллюстрации к решению приведены на рисунке 4.

Рисунок 4. Метод Эйлера модифицированный.

Проведем решение в несколько этапов:

2. Через точку А проведем прямую под углом α, где tg α = f(x_i, y_i);

3. На этой прямой найдем точку С(х_i + h/2, y_i + h/2 ∙ f(x_i, y_i));

4. Через точку С проведем прямую под углом α1, где tg α1 = f(x_i + h/2,y_i + h/2 ∙ f(x_i, y_i));

5. Через точку А проведем прямую, параллельную последней прямой;

7. После проведения вычислений, аналогичных вычислениям, описанным в методе Эйлера, получим формулу для определения значения у_i₊₁:

Модифицированный метод Эйлера дает меньшую погрешность. На рисунке 4 это хорошо видно. Так величина εl характеризует погрешность метода Эйлера, а ε — погрешность метода Эйлера модифицированного.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным приведена на рисунке 5.

EilerM(X0, Xk, Y0, N, Y)

F(x, у) — заданная функция — должна

быть описана отдельно.

h = (Xk – X0)/N

Входные параметры:
Х0, XК — начальное и конечное

i = 0, …, N-1

значения независимой

переменной;

x = X0 + i ∙ h

Y0 – значение y₀ из начального условия

y(x₀)=y₀;

Y_i+1 = Y_i + h ∙ F(x + h/2, Y_i + h/2 ∙ F(x_i, y_i))

N — количество отрезков разбиения;

Y — массив значений искомого решения

End

в узлах сетки.

Рисунок 5. Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным.

Решение поставленной задачи методами Эйлера и Эйлера модифицированного.

Метод Эйлера.

1. Строим оси координат;

2. Отмечаем A(0; -1.8) – первую точку интегральной кривой;

3. Ищем угол наклона касательной к графику в точке A:

4. Строим касательную l₀ в точке А под углом α₀;

5. Находим х₁ по формуле: x_i = х₀ + ih, где h – шаг интегрирования

6. Проводим прямую x = x₁ = 1,2 до пересечения с прямой l₀, отмечаем точку B(x₁; y₁);

7. Ищем y точки B:

Из прямоугольного треугольника ABC ,

Следовательно, точка B имеет координаты (1.2; -1.8).

Предиктор-корректор или модифицированный метод Эйлера для решения дифференциального уравнения

Для заданного дифференциального уравнения с начальным условием
найти приближенное решение, используя метод Predictor-Corrector.

Метод Предиктор-Корректор:
Метод предиктор-корректор также известен как метод Модифицированного Эйлера .
В методе Эйлера касательная рисуется в точке, а наклон рассчитывается для заданного размера шага. Таким образом, этот метод лучше всего работает с линейными функциями, но для других случаев остается ошибка усечения. Для решения этой проблемы введен модифицированный метод Эйлера. В этом методе вместо точки среднее арифметическое наклона за интервал используется.

Таким образом, в методе Predictor-Corrector для каждого шага прогнозируемое значение сначала рассчитывается по методу Эйлера, а затем наклоны в точках и рассчитывается и среднее арифметическое этих склонов добавляются к рассчитать скорректированное значение ,

Шаг — 1: сначала прогнозируется значение для шага (здесь t + 1):

,
здесь h — размер шага для каждого приращения

Шаг — 2: Затем прогнозируемое значение корректируется :

Шаг — 3: Увеличение сделано:

Шаг 4: Проверить продолжение, если

затем перейдите к шагу — 1.

Шаг 5: Завершить процесс.

Как и в этом методе, используется средний уклон, поэтому ошибка значительно уменьшается. Также мы можем повторить процесс коррекции сходимости. Таким образом, на каждом шаге мы уменьшаем ошибку, таким образом, улучшая значение y.

Примеры:

The final value of y at x = 1 is y=2.18147

Реализация: здесь мы рассматриваем дифференциальное уравнение:

// C ++ код для решения дифференциального уравнения
// используя метод Predictor-Corrector или Modified-Euler
// с заданными условиями, y (0) = 0,5, размер шага (h) = 0,2
// найти y (1)

using namespace std;

// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v

double f( double x, double y)

double v = y — 2 * x * x + 1;

// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера

double predict( double x, double y, double h)

// возвращается значение следующего y (прогнозируемого)

double y1p = y + h * f(x, y);

// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера

double correct( double x, double y,

double x1, double y1,

// (x, y) предыдущего шага

// и x1 — увеличенный x для следующего шага

// и у1 прогнозируется у для следующего шага

double e = 0.00001;

y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));

> while ( fabs (y1c — y1) > e);

// каждая итерация корректирует значение

// of y используя средний уклон

void printFinalValues( double x, double xn,

double y, double h)

double x1 = x + h;

double y1p = predict(x, y, h);

double y1c = correct(x, y, x1, y1p, h);

// на каждой итерации сначала значение

// для следующего шага сначала прогнозируется

// а затем исправлено.

cout «The final value of y at x = «

// здесь x и y являются начальными

// заданное условие, поэтому x = 0 и y = 0.5

double x = 0, y = 0.5;

// конечное значение x, для которого требуется y

printFinalValues(x, xn, y, h);

// Java-код для решения дифференциала
// уравнение с использованием Predictor-Corrector
// или модифицированный метод Эйлера с
// заданные условия, y (0) = 0,5, шаг
// размер (h) = 0,2, чтобы найти y (1)

// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v

static double f( double x, double y)

double v = y — 2 * x * x + 1 ;

// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера

static double predict( double x, double y, double h)

// возвращается значение следующего y (прогнозируемого)

double y1p = y + h * f(x, y);

// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера

static double correct( double x, double y,

double x1, double y1,

// (x, y) предыдущего шага

// и x1 — увеличенный x для следующего шага

// и у1 прогнозируется у для следующего шага

double e = 0.00001 ;

y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));

while (Math.abs(y1c — y1) > e);

// каждая итерация корректирует значение

// of y используя средний уклон

static void printFinalValues( double x, double xn,

double y, double h)

double x1 = x + h;

double y1p = predict(x, y, h);

double y1c = correct(x, y, x1, y1p, h);

// на каждой итерации сначала значение

// для следующего шага сначала прогнозируется

// а затем исправлено.

DecimalFormat df = new DecimalFormat( «#.#####» );

System.out.println( «The final value of y at x = » +

x + » is : » +df.format(y));

public static void main (String[] args)

// здесь x и y являются начальными

// заданное условие, поэтому x = 0 и y = 0.5

double x = 0 , y = 0.5 ;

// конечное значение x, для которого требуется y

printFinalValues(x, xn, y, h);

// Этот код предоставлен mits

# Python3 код для решения дифференциального уравнения
# с использованием метода Predictor-Corrector или Modified-Euler
# с заданными условиями, y (0) = 0,5, размер шага (h) = 0,2
# найти y (1)

# рассмотрим дифференциальное уравнение
# для заданных x и y, вернуть v

v = y — 2 * x * x + 1 ;

# предсказывает следующее значение для данного (x, y)
# и размер шага h методом Эйлера

def predict(x, y, h):

# значение следующего y (прогнозируемого) возвращается

y1p = y + h * f(x, y);

# исправляет прогнозируемое значение
# с использованием модифицированного метода Эйлера

def correct(x, y, x1, y1, h):

# (x, y) предыдущего шага

# и x1 — увеличенный x для следующего шага

# и y1 прогнозируется y для следующего шага

while ( abs (y1c — y1) > e + 1 ):

y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));

# каждая итерация корректирует значение

# у, используя средний наклон

def printFinalValues(x, xn, y, h):

y1p = predict(x, y, h);

y1c = correct(x, y, x1, y1p, h);

# на каждой итерации сначала значение

# для следующего шага сначала прогнозируется

# а затем исправлено.

print ( «The final value of y at x =» ,

if __name__ = = ‘__main__’ :

# здесь x и y являются начальными

# заданное условие, поэтому x = 0 и y = 0.5

# конечное значение x, для которого требуется y

printFinalValues(x, xn, y, h);

# Этот код предоставлен Rajput-Ji

// C # код для решения дифференциала
// уравнение с использованием Predictor-Corrector
// или модифицированный метод Эйлера с
// заданные условия, y (0) = 0,5, шаг
// размер (h) = 0,2, чтобы найти y (1)

// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v

static double f( double x, double y)

double v = y — 2 * x * x + 1;

// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера

static double predict( double x, double y, double h)

// возвращается значение следующего y (прогнозируемого)

double y1p = y + h * f(x, y);

// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера

static double correct( double x, double y,

double x1, double y1,

// (x, y) предыдущего шага

// и x1 — увеличенный x для следующего шага

// и у1 прогнозируется у для следующего шага

double e = 0.00001;

y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));

while (Math.Abs(y1c — y1) > e);

// каждая итерация корректирует значение

// of y используя средний уклон

static void printFinalValues( double x, double xn,

double y, double h)

double x1 = x + h;

double y1p = predict(x, y, h);

double y1c = correct(x, y, x1, y1p, h);

// на каждой итерации сначала значение

// для следующего шага сначала прогнозируется

// а затем исправлено.

Console.WriteLine( «The final value of y at x = » +

x + » is : » + Math.Round(y, 5));

static void Main()

// здесь x и y являются начальными

// заданное условие, поэтому x = 0 и y = 0.5

double x = 0, y = 0.5;

// конечное значение x, для которого требуется y

printFinalValues(x, xn, y, h);

// Этот код предоставлен mits

// PHP-код для решения дифференциального уравнения
// используя Predictor-Corrector или Modified-Euler
// метод с заданными условиями, y (0) = 0,5,
// размер шага (h) = 0,2, чтобы найти y (1)

// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v

function f( $x , $y )

$v = $y — 2 * $x * $x + 1;

// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера

function predict( $x , $y , $h )

// возвращается значение следующего y (прогнозируемого)

$y1p = $y + $h * f( $x , $y );

// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера

function correct( $x , $y , $x1 , $y1 , $h )

// (x, y) предыдущего шага и

// х1 — увеличенный х для следующего шага

// и у1 прогнозируется у для следующего шага

$y1c = $y + 0.5 * $h * (f( $x , $y ) +

> while ( abs ( $y1c — $y1 ) > $e );

// каждая итерация корректирует

// значение y с использованием среднего наклона

function printFinalValues( $x , $xn , $y , $h )

$y1p = predict( $x , $y , $h );

$y1c = correct( $x , $y , $x1 , $y1p , $h );

// на каждой итерации сначала значение

// для следующего шага сначала прогнозируется

// а затем исправлено.

echo «The final value of y at x = » . $x .

» is : » . round ( $y , 5) . «\n» ;

// здесь x и y являются начальными

// заданное условие, поэтому x = 0 и y = 0.5

// конечное значение x, для которого требуется y

printFinalValues( $x , $xn , $y , $h );

// Этот код предоставлен mits
?>

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

источники:

http://espressocode.top/predictor-corrector-or-modified-euler-method-for-solving-differential-equation/

http://1cov-edu.ru/differentsialnye-uravneniya/lineinie_postoyannie_koeffitsienti/eilera/