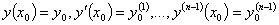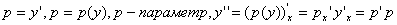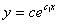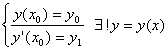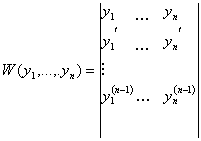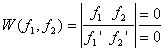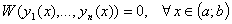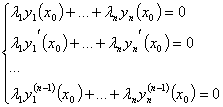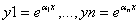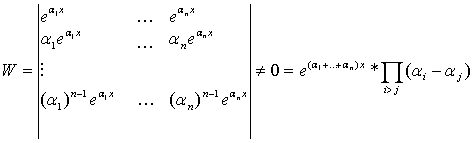Дифференциальное уравнение n ного порядка
Дифференциальное уравнение n — ного порядка.
Дифференциальным уравнением n — ного порядка называется уравнение вида: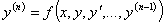 
для нахождения единственного решения неоюходимо знать начальные условия 
Уравнения допускающие понижение порядка.
Можно отыскать решение этого уравнения, если уравнение имеет один из нижеследующих видов:
1) 
, решается двойным интегрированием.
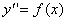
2) 
, делаем замену y ’= p = p ( x ), y ’’= p ’
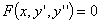
3) 
, тогда 
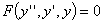
обозначим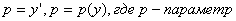 
, тогда pp ’ y = p 2
рассмотрим несколько случев
2) p ¹ 0 => p ¢ y=p или p ¢ /p=1/y => dp /p= dy /y
lnp = lny+c , p=cy, y ¢ =cy, dy /y= cdx => 
Линейные дифференциальные уравнения
Линейным дифференциальным уравнением называется уравнение вида:
(1)
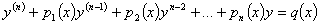
При q =0, уравнение называется однородным, q ¹ 0 неоднородным.
y ¢ + py = q –дифференциальное уравнение первого порядка.
y ¢ ¢ + p 1 y ¢ + p 2 y =0. если p 1 и p 2 непрерывны в рассматриваемой области, то $ ! 1-ая диф . кривая => единственное решение дифференциального уравнения.
Обозначим левую часть уравнения (1) при q ( x )=0 L ( y )=> L ( y )=0.
Отметим два свойства L ( y ).
Линейная зависимость функций
Функции y 1 ,…, yn называются линейно зависимыми, если $ λ1 ,…, λ n (| λ 1 |+…+| λn | ¹ 0) такие что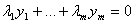 
соответственно функции называются линейно независимыми если не удовлетворяют уравнению (1).
Если функции y 1 ( x ),…, yn ( x )(все функции и их производные непрерывны и существуют до n -1 го порядка) линейно зависимы, то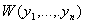 
=0.
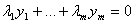
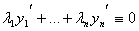
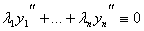
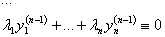
Так как функции линейно зависимы, то после дифференциирования получим:
, 
Эта система имеет ненулевое решение ó когда определитель этой системы равен 0. А этот определитель и есть определитель Вронского.
Если W ¹ 0 хотя бы в одной точке то функции линейно независимы.
Покажем, что если определитель равен нулю, то функции необязательно линейно зависимы.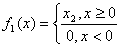 
, 
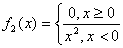
Рассмотрим произвольную точку x 0 >0.
Утв . Если функции линейно независимы, то W =0
Если W =0, то неизвестно зависимы функции или нет.
Если W ¹ 0 в какой-либо точке, то функции линейно независимы.
Теорема 2 П усть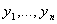 
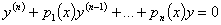
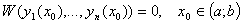
решения уравнения 
и 
тогда 
Следствие: если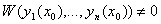 
хотя бы в одной точке ( a , b ) тогда » x ‘ ( a , b ) W ( x ) ¹ 0.
Так как W =0 в x 0 , то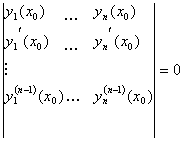 
так как определитель =0 то его строки и столбцы и строки линейно зависимы (их линейная комбинация равна 0). Значит
Рассмотрим функцию y =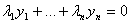 
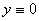
L ( y )=0, т.е. y — решение дифференциального уравнения. Следовательно , 
(*) ( первая строка в системе). Решение 
удовлетворяет (1) но начальным условиям удовлетворяет только одно решение (по теореме о существовании единственного решения). Получаем, что W =0 » x э ( a , b ).
y ( n ) =0 Решения: y 1 =1, y 2 = x , y 3 = x 2 ,…, yn = x n -1
этот определитель равен произведению чисел на главной диагонали (а все эти числа отличны от нуля), следовательно определитель отличен от нуля, следовательно функции линейно независимы.
Значит функции линейно независимы .
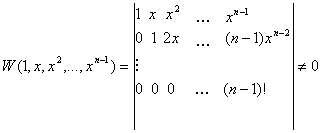
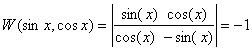
Фундаментальная система решений есть полная система решений дифференциального уравнения.