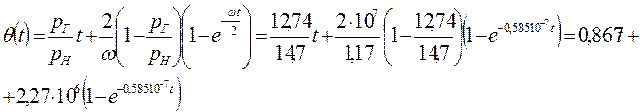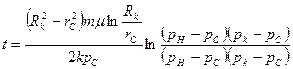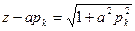Дифференциальное уравнение нестационарной фильтрации газа

Дифференциальные уравнения

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ФИЛЬТРАЦИИ ЖИДКОСТЕЙ И ГАЗОВ

Общие положения.

Процессы, происходящие в нефтяных и газовых пластах при разработке нефтяных и газовых месторождений, существенно зависят от времени, т.е. являются нестационарными. Характеристики движения жидкости или газа — давление, скорость фильтрации и т.п. изменяются от точки к точке продуктивного пласта и образуют нестационарное поле давлений, скоростей фильтрации и т.п . Задачи нестационарной фильтрации жидкости или газа в пласте решаются методом математической физики; для этого составляются и интегрируются соответствующие дифференциальные уравнения.

К числу дифференциальных уравнений относятся:

1. дифференциальные уравнения движения жидкости или газа;

2. уравнение баланса массы в элементе пористой среды — уравнение неразрывности (сплошности) фильтрационного потока.

Дополнительно к дифференциальным уравнениям вводятся уравнения состояния флюида и пористой среды, определяемые параметрами .

В итоге получаем замкнутую систему уравнений, т.е число уравнений в системе равно числу неизвестных функций, характеризующих рассматриваемый фильтрационный процесс и подлежащих определению.

Для получения решения системы уравнений должны быть заданы начальные (при t=0) и краевые (граничные) условия — на границах пласта. При этом заметим, что фильтрация представляет собой очень медленный процесс и изменение температуры флюида в ходе движения (вследствие наличия сопротивления и расширения вещества) успевает компенсироваться теплообменом с окружающими горными породами. Поэтому считаем, что температура флюида равна температуре пористой среды и неизменна, т.е. Т_ф=Т_с=Т=const; это означает, что фильтрация считается изотермическим процессом.

В результате интегрирования полученных итоговых дифференциальных уравнений фильтрации получаем закон распределения давления, а, следовательно, и скорости фильтрации по всему пласту в любой момент времени, т.е. Р=Р(x,y,z,t); u_x=u_x(x,y,z,t); u_у=u_у(x,y,z,t), u_z=u_z(x,y,z).

Если принять жидкость несжимаемой (r=const) в недеформируемой пористой среде (m=const,k=const) – самый упрощенный случай, то число искомых функций ограничится этими четырьмя параметрами (Р,V_x,V_y,V_z).

Если предполагается фильтрация сжимаемого флюида в сжимаемой пористой среде, предстоит еще дополнительно определить значения параметров r,m,k,m как функции координат и времени. В этом случае имеем восемь уравнений — дифференциальных и конечных- для определения восьми характеристик фильтрационного потока, жидкости (газа) и пористой среды. Аналитическое решение системы диф. уравнений в этом (общем) случае невозможно; необходимо численное решение с применением ЭВМ.

Дифференциальные уравнения

Движения флюида

Дифференциальные уравнения движения флюида получаются непосредственно из закона Дарси для трубки тока переменного сечения (рис.4)

, (2.1)

где Р — приведенное давление, Р=Р(S,t) .

Или в векторной форме:

. (2.2)

При этом предполагается изотропность пористой среды, т.е. предполагается постоянство проницаемости k по всем направлениям в окрестности рассматриваемой точки.

Представим вектор скорости фильтрации через составляющие по координатным осям:

= V_x*`i + V<sub>y</sub>*`j +V_z*`k (а)

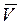
Дата добавления: 2016-06-13 ; просмотров: 1828 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

XIII. НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ГАЗА

Дифференциальное уравнение неустановившейся изотерми­ческой фильтрации идеального газа по закону Дарси имеет вид

(XIII.1)

(XIII.2)

Это уравнение является нелинейным уравнением параболи­ческого типа, оно отличается от дифференциального уравнения упругого режима тем, что искомой функцией является не дав­ление р, а квадрат давления р 2 , а вместо постоянного коэффи­циента пьезопроводности х в уравнение входит переменная вели­чина kp/mx.

Точные решения нелинейного уравнения (XIII.2) получены только для некоторых частных задач. Как правило, это урав­нение интегрируется приближенными методами.

Наиболее простым приближенным методом является метод линеаризации, предложенный И. А. Чарным, в котором переменное значение коэффициента kp/mµ заменяется усредненным значением kp_ср/mµ, где

здесь р_max и р_min — максимальное и минимальное давления в залежи за расчетный период, или

При такой замене уравнение (XIII.2) приводится к линей­ному дифференциальному уравнению теплопроводности. Это дает возможность нестационарное движение газа рассчитывать жак движение упругой жидкости по формулам упругого ре­жима фильтрации.

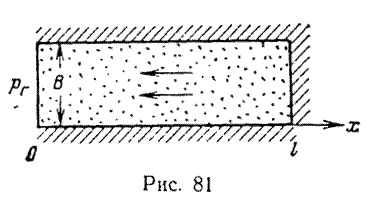
Л. С. Лейбензоном было лолучено решение задачи об истечении газа из полосообразного замкнутого пласта при условии постоянного давления на галерее (рис. 81). Задача сводится к интегрирова­нию дифференциального уравнения

(XIII.3)

при начальном и граничных условиях:

при t=0

при x=0

при x=l (XIII.4)

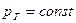
— условие на непроницаемой границе газового пласта.

Задача решалась методом последовательных приближений.

В первом приближении коэффициент, входящий в правую часть (XIII.3), считается постоянным и равным .

При этом (XIII.3) обращается в уравнение теплопроводно­сти, интеграл которого при условиях (XII 1.4) имеет вид

(XIII.5)

Во втором приближении принимается, что переменное дав­ление p, входящее в коэффициент kp/mµ, зависит только от времени t и выражается формулой

(XIII.6)

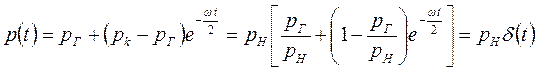
далее, введя новую переменную

(XIII.7)

приведем (XIII.3) к уравнению теплопроводности

(XIII.8)

решение которого при условиях (XIII.4) дается уравнением (XIII.5), в котором переменная t должна быть заменена на θ:

(XIII.9)

Объемный дебит галереи, приведенный к атмосферному дав­лению, можно записать в виде

(XIII.10)

Многие задачи неустановившейся фильтрации газа решаются «приближенно по методу последовательной смены стационарных состояний с привлечением уравнения материального баланса газа.

Если газовая залежь замкнута, то отобранное за время dt количество газа по объему, приведенному к атмосферному дав­лению и пластовой температуре, равное , равно изменению запасов газа в пласте за тот же промежуток времени.

Если объем порового пространства Ω постоянный, газ идеаль­ный, а фильтрация изотермическая, то изменение запасов можно представить в виде , где dp — изменение средневзвешенного по объему давления в газовой залежи за промежуток dt. Урав­нение

(XIII.11)

называется дифференциальным уравнением истощения газовой залежи.

При неустановившейся плоскорадиальной фильтрации газа средневзвешенное давление мало отличается от контурного, поэтому, заменяя на p_k записывают уравнение истощения газовой залежи в виде

(XIII.12)

Уравнение (XIII. 12) в сочетании с методом последователь­ной смены стационарных состояний позволяет определять рас­пределение давления по пласту, изменение давления с течением времени в любой точке пласта, изменение во времени дебитов таза при эксплуатации залежи с различными условиями на забое. Такими простейшими условиями являются следующие: ..a) Q_aт = const; б) p_c = const; в) , где c = 2nr_chw_max, a w_max — максимально допустимая скорость фильтрации газа, ис­ключающая возможность выноса песка и образования песчаных пробок.

Определить падение давления р_к на внешней границе полосообразной газовой залежи длиной l = 7500 м, шириной В = 800 м, мощностью h= 10 м (см. рис. 81), если коэффициент пористости пласта m = 20%, коэффициент проницаемости k = 0,5 Д, коэф­фициент вязкости µ = 0,014 мПа•с, начальное пластовое давле­ние р_н = 14,7МПа (150 кгс/см 2 ). Давление на выходе газа в галерею постоянно и равно р_г= 12,74 МПа (130 кгс/см 2 ).

Найти также приведенный к атмосферному давлению и пла­стовой температуре расход газа Q_ат и распределение давления по длине пласта через t = 30 сут после начала отбора газа из галереи.

Решение.Для определения падения давления во времени на границе пласта р_к(t) и распределения давления по длине пла­ста р(х) в момент t = 30 сут используем решение Л. С. Лейбеизона по методу последовательных приближений (XIII.9).

Прежде всего подсчитаем значение параметра

и значения переменной Q(t) в разные моменты

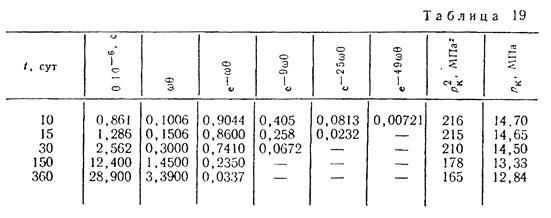
а результаты поместим в табл. 19.

По формуле Л. С. Лейбензона на границе пласта (при x=l) имеем

Значения величин, входящих в эту формулу, приведены в табл. 19.

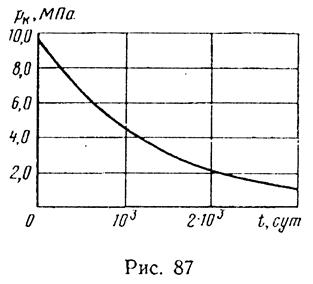
На рис. 82 представлен график зависимости р_к(t).

Закон распределения давления по пласту через 30 сут = 2,59•10 6 с после начала отбора:

Результаты расчетов даны в табл. 20. На рис. 83 показана кривая изменения давления по пласту.

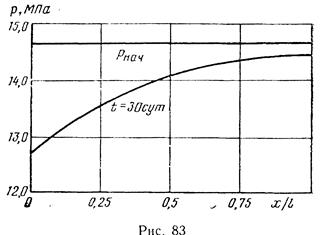
Расход газа, приведенный к атмосферному давлению и пла­стовой температуре, найдем по (XIII.10).

Газовая скважина расположена в центре кругового замкну­того пласта радиусом R_к=1000 м, мощностью h = 8 м и эксллуатируется при постоянном давлении на забое p_c = 6,86 МПа (70 кгс/см 2 ). .Начальное давление в газовой залежи р_н = 11,76 МПа (120 кгс/см 2 ), коэффициент проницаемости пласта k = 800 мД, коэффициент пористости пласта m=18%, динами­ческий коэффициент вязкости газа µ = 0,013 мПа•с, радиус скважины r_с= 10 см.

Найти изменение во времени давления на внешней границе залежи p_k(t) и приведенного объемного дебита скважины.

Решение.Полагая, что средневзвешенное пластовое давление газа равно давлению на внешнем контуре р_к, решим задачу методом последовательной смены стационарных состояний. За время dt при изотермическом процессе из залежи отбирается количество газа (по объему, приведенному к атмосферному давлению)

(XIII.13)

(XIII.14)

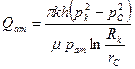
и подставляя эти выражения в уравнение материального ба­ланса (XIII.13), получим

Подставляя исходные данные подсчитаем для различных р_к значения t:

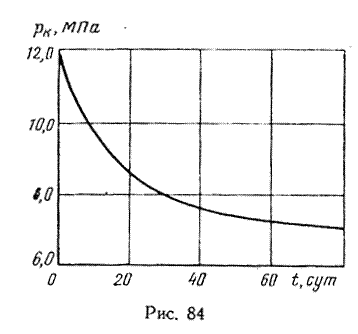
Результаты подсчетов представлены на рис. 84 и ниже.

p_k, МПа …………..11,76 10,78 9,8 8,82 7,84 6,96

t, сут ………………0 3,77 8,88 16,5 30,5 80,5

Q_ат ,м 3 /cут ……….13,4·10 6 10,1·10 6 7,2·10 6 4,51·10 6 2,11·10 6 1,99·10 5

Подставляя найденные значения р_к в (XIII.14), найдем из­менение Qат во времени

Cоответствующие значения дебатов даны на рис. 85.

Определить время истощения газовой залежи и изменение во времени давления на внешней границе и на забое скважины, считая, что скважина дренирует круговую зону радиуса R_к = = 500 м и эксплуатируется с постоянным приведенным дебитом Qaт = 500 000 м 3 /сут. Начальное пластовое давление р_н = 9,8 МПа (100 кгс/см 2 ), конечное давление на забое газовой скважины (Р_с)_кон = 0,101 МПа (1,033 кгс/см 2 ), мощность пласта h=12 м, радиус скважины r_с=10 см, коэффициент проницаемости пласта k = 500 мД, коэффициент пористости m==20%, динамический коэффициент вязкости газа µ = 0,015 мПа·с.

Решение. Из уравнения материального баланса, в котором средневзвешенное пластовое давление заменено контурным, имеем

(XIII.15)

Интегрируя (XIII. 15) по р_к в пределах от р_н до р_к и по t ют 0 до t получим

(XIII.16)

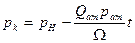
Из формулы дебита

найдем давление на забое скважины

(XIII.17)

По значению забойного давления в конце разработки р_с.кон .найдем конечное значение давления на внешней границе р_к.кон.

Подставляя полученное зна­чение р_к.кон в (XIII.16), найдем время истощения газовой залежи:

Изменение во времени р_к и р_с определяется из (XIII.16) и (ХШ.17).

Результаты подсчетов приведены на рис. 86 и ниже.

t, сут. О 50 100 150 200 291

р_к, кгс/см 2 . 100 86,3 72,6 58,9 45,2 20,2

р_с, кгс/см 2 . 97,9 83,9 69,7 55,3 40,5 1,033

Определить изменение во времени дебита газовой скважины, давления на внешней непроницаемой границе р_к(t) и давления на забое скважины р_с(t) эксплуатирующейся при поддержании постоянной скорости движения газа в призабойной зоне пласта. Начальное пластовое давление р_н =9,8 МПа (100 кгс/см 2 ), ра­диус контура зоны дренирования R_k = 750 м, мощность пласта h=10 м, коэффициент проницаемости пласта k = 0,3 Д, коэффициент пористости пласта m = 20%, динамический коэффици­ент вязкости газа в пластовых условиях µ = 0,012 сП, радиус скважины r_с = 0,1 м. Коэффициент с, который соответствует максимально допустимой скорости фильтрации в призабойной зоне, определяемый практически, равен . Принять атмосферное давление р_ат = 0,098 МПа (1 кгс/см 2 ).

Решение.Если газ отбирается при поддержании мак­симально допустимой скорости фильтрации w_max у забоя скважины, то приведенный дебит

(XIII.18)

(XIII.19)

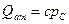
С другой стороны,

(XIII.20)

Приравнивая соотношения (XIII.19) и (XIII.20), найдем

Обозначая , запишем

(XIII.21)

Подставляя (XIII.21) в (XIII.19), найдем зависимость дебита Q_ат от p_k

Из уравнения материального баланса, заменяя среднее пла­стовое давление контурным, найдем

(XIII.22)

Вводя новую переменную

и интегрируя дифференциальное уравнение (XI 11.22), получим

(XIII.23)

Подсчитаем объем норового пространства

Подставляя численные значения параметров а_, с, р_ат и р_н в соотношение (XIII.23), задаваясь различными значениями р_к, определим значения t. Соответствующие значения p_c(t) и Q_ат найдем из выражений (XIII.19) и (XIII.21). Результаты вы­числений представлены на рис. 87, 88 и ниже.

t,сут ………………0 226 462 776 1196 1825 3130 4250 6100

p_{k ,} МПа…………9,8 8,33 6,86 5,39 3,92 2,45 0,980 0,490 0,210

p_c ,МПа…………9,62 8,15 6,68 5,22 3,74 2,28 0,822 0,345 0,098

Q_ат ·10 -5 ,м 3 /сут..2,66 2,25 1,85 1,445 1,035 0,632 0,227 0,0955 0,0271

Неустановившееся движение газа в пористой среде (дифференциальные уравнения Л.С. Лейбензона)

Автор работы: Пользователь скрыл имя, 01 Июня 2013 в 20:31, курсовая работа

Краткое описание

Подземная гидромеханика – наука о движении жидкостей, газов и их смесей в пористых и трещиноватых горных породах. Она является той областью гидромеханики, в которой рассматривается не движение жидкостей и газов вообще, а особый вид их движения- фильтрация, которая имеет свои специфические особенности. Она служит теоретической основой разработки нефтяных, газовых и газоконденсатных месторождений. Вместе с тем методами теории фильтрации решаются важнейшие задачи гидрогеологии, инженерной геологии, гидротехники, химической технологии и т. д. Расчет притоков жидкости к искусственным водозаборам и дренажным сооружениям, изучение режимов естественных источников и подземных потоков, расчет фильтрации воды в связи с сооружением и эксплуатацией плотин, понижением уровня грунтовых вод, проблемы подземной газификации угля, задачи о движении реагентов через пористые среды и специальные фильтры, фильтрация жидкостей и газов через стенки пористых сосудов и труб – вот далеко не полный перечень областей широкого использования методов теории фильтрации.

Вложенные файлы: 1 файл

Курсовая Подземка.docx

Уравнение (6) получено с использованием в качестве уравнения движения закона Дарси. Вместе с тем, последующие исследования И.А. Чарного, Е. М. Минского и других показали, что при фильтрации газов в природных пластах в большинстве случаев следует пользоваться нелинейным (двучленным) законом фильтрации. Математические труд-ности в решении получающегося при этом дифференциального уравнения еще более возрастают.

Отметим, что одним из эффективных путей решения уравнения Лейбензона является линеаризация, т. е. сведение его к линейному уравнению Фурье. Как покажем при дальнейшем рассмотрении, в некоторых практических случаях использование различных способов линеаризации уравнения (6) позволяет получать приближенные решения, удовлетворяющие требованиям практики.

1.2 Вывод дифференциального уравнения неустановившейся фильтрации совершенного газа по двучленному закону

Будем считать пласт недеформируемым, фильтрацию изотермической и происходящей по двучленному закону. Рассмотрим плоскорадиальный поток к осесрмметрично расположенной скважине.

Воспользуемся уравнением неразрывности для плоскорадиального движения

Воспользовавшись выражением для массовой скорости , получим

линеаризация уравнение фильтрация газ

Подставив выражения (11), (12) и (5) в уравнение неразрывности (10) и сократив на , получим

Если сделать замену , то дифференциальное уравнение

неустановившейся фильтрации газа по двучленному закону примет следующий вид

Аналитическое решение уравнения (14) наталкивается на значительные трудности, однако численное решение для обычных в подземной гидромеханике начальных и граничных условий не представляет затруднений.

§ 2. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЯ ЛЕЙБЕНЗОНА И ОСНОВНОЕ РЕШЕНИЕ ЛИНЕАРИЗОВАННОГО УРАВНЕНИЯ

Если заменить нелинейное дифференциальное уравнение (8) линейным, т.е. линеаризовать его, то оно упростится – для линейного уравнения существуют точные аналитические решения. Ясно, что эти точные решения линеаризованного уравнения будут приближенными для нелинейного. Оценить погрешность решения, которая возникает при замене точного уравнения линеаризованным, можно, например, сравнивая приближенное решение с решением на ЭВМ точного уравнения.

Были предложены различные способы линеаризации уравнения (8). Если рассматривается плоскорадиальный приток к скважине, то из теории установившейся фильтрации газа, воронка депрессии очень крутая, и в большей части пласта давление мало отличается от контурного. На этом основании Лейбензон предложил заменить переменное давление р в коэффициенте уравнения (8) на постоянное давление равное начальному давлению в пласте. Тогда, обозначив , получим вместо уравнения (8) уравнение

которое является линейным уравнением пьезопроводности относительно функции р 2 где — константа, аналогичная коэффициенту пьезопроводности. Такой способ линеаризации, когда переменный коэффициент и в уравнении (15) при различных значениях давления принимается константой, называется линеаризацией по Лейбензону. В дальнейшем различными авторами были предложены уточнения к линеаризации по Лейбензону. Так, И. А. Чарный предложил свести уравнение (8) к линейному заменой переменного давления в коэффициенте на значение

где — максимальное и минимальное давления в газовой залежи на расчетный период.

Для плоскорадиальной фильтрации газа (15) запишется следующим образом

Здесь выражение представляет собой оператор Лапласа

в полярных координатах относительно квадрата давления для плоско-радиального движения.

Уравнение (16) надо проинтегрировать при начальном условии

и при граничном условии в удаленных точках

Выведем условие для давления на забое скважины. Для этого запишем выражение для массового дебита исходя из закона Дарси в дифференциальной форме для плоскорадиальной фильтрации:

и сократив на , получим:

Из этого соотношения выразим условие на стенке газовой скважины бесконечно малого радиуса:

Решением поставленной задачи для упругой жидкости является основная формула упругого режима :

Аналогия между фильтрацией упругой жидкости и газа свидетельствует о том, что, заменив в формуле (20) давление на р 2 , a – на , -на получим решение поставленной задачи для, газа

Рис.1. Кривые распределения давления по пласту при неустановившемся притоке газа к скважине в разные моменты времени (а) и динамика давления в фиксированных точках пласта (б)

Это и есть основное решение линеаризованного уравнения Лейбензона.

Для малых значений аргумента можно заменить интегральную показательную функцию логарифмической

Подчеркнем, что решения (21)-(24) являются приближенными, так как получены в результате интегрирования линеаризованного уравнения (16), а не точного (6).

Формулы (22) и (24) определяют (при фиксированных значениях времени t) распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t = 0. Эти депрессионные кривые имеют такой же характер, как при установившейся фильтрации — они очень крутые вблизи скважины (рис. 1.а). Если задать значение r, то можно найти изменение давления в данной точке с течением времени. В частности, можно найти изменение давления на забое (при r = ) после начала работы скважины (рис.1.б)

§ 3. ТОЧНОЕ РЕШЕНИЕ ОДНОЙ АВТОМОДЕЛЬНОЙ ЗАДАЧИ ОБ ОСЕСИММЕТРИЧНОМ ПРИТОКЕ ГАЗА К СКВАЖИНЕ С ПОСТОЯННЫМ ДЕБИТОМ

В § 2 приведено решение задачи о нестационарном притоке совершенного газа к скважине бесконечно малого радиуса с постоянным дебитом. Решение получено в результате интегрирования линеаризованного дифференциального уравнения.

Г. И. Баренблатт, применяя анализ размерностей, показал, что нелинейное уравнение Лейбеизона при определенных начальных и граничных условиях имеет точное решение. Это имеет важное значение, так как полученное точное решение может служить эталоном для сравнения с ним приближенных решении.

Как и в § 2, рассматривается задача о нестационарном плоскорадиальном притоке газа с постоянным дебитом к скважине в бесконечном пласте. В этом случае необходимо проинтегрировать нелинейное уравнение Лейбензона

при тех же начальных и граничных условиях (17); (18), (19).

Г. И. Баренблаттом показано, что в такой постановке задача автомодельна, т. е. давление зависит от некоторого единого комплекса, включающего в себя обе переменные -r и t, а дифференциальное уравнение в частных производных (26) приводится к обыкновенному дифференциальному уравнению, которое легко интегрируется. Чтобы установить, от каких аргументов будет зависеть давление, проведем анализ размерностей.

Распределение давления в пласте зависит, как следует из постановки задачи, от пяти определяющих параметров (n = 5): r, t, , , .

Если обозначить размерность длины через L, размерность времени Т, размерность давления [р], то размерности этих параметров выразятся следующим образйм

[r]=L, [t]-Т, [ ]=[р], [ ]=L 2 [p] -1 T -1 , [ ]=[p 2 ]

Среди этих параметров – три с независимыми размерностями: r, t, (k = 3). Как следует из П-теоремы, искомая функция-давление, приведенное к безразмерному виду F = р/р_к будет зависеть от двух безразмерных комплексов (п — k = 5 — 3 = 2), Легко проверить, что такими безразмерными комплексами являются следующие