Дифференциальное уравнение описывает вынужденные колебания

Вынужденные колебания

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $\delta $ — коэффициент затухания; $<\omega >_0$ — циклическая частота свободных незатухающих колебаний (если $\delta $=0, то $<\omega >_<0\ >$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $\delta =\frac<2L>$ — коэффициент затухания; $<\omega >_0=\frac<1><\sqrt>$; $U=U_m<\cos \left(\omega t\right)\ >$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=\frac$ если колебания механические ($x_0=\frac-\ в\ случае\ электрических\ колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $\omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $\omega $.

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(\omega )$. Взяв производную $\frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($<\omega >_r$) равна:

При $<\delta >^2\ll <\omega >^2_0$ резонансная частота совпадает с собственной частотой колебаний $<\omega >_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $<\delta >^2\ll <\omega >^2_0$) амплитуда при резонансе равна:

где $Q=\frac<<\omega >_0><2\delta >$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Примеры задач с решением

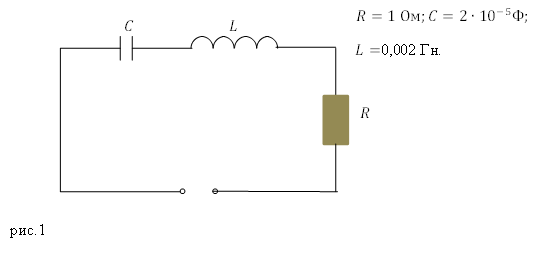
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=<\cos \left(\omega t\right)(Н).\ \ \ >$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $\delta =\frac<2m>$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Дифференциальное уравнение вынужденных колебаний и его интегрирование

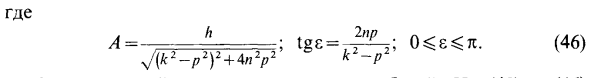
Дифференциальное уравнение вынужденных колебаний и его интегрирование

• Чтобы прояснить влияние линейного сопротивления на вынужденную вибрацию, рассмотрим наиболее распространенный случай, когда обобщенная сила Q состоит из трех сил. Потенциал Qn = —dP / dq— —eq, линейное сопротивление b (φ, = −dF / da = — == Hsin (pz + 8). Подставляя это значение обобщенной силы Q = Q «+ Q’t + QB в уравнение Лагранжа (1), aq + \ uj + cq = Hsm (pi + 5). Разделим обе части уравнения на π и введем обозначение k2 = c / a, 2n = c / a, h = Hja. Где A: круговая частота естественной вибрации.

Коэффициент демпфирования, а h относительная амплитуда возмущающей силы. Окончательный вид дифференциального уравнения: q + 2nq + k2q = hs \ n (pt-y8). (44) Линейное дифференциальное уравнение получается с постоянным фактором вынужденной вибрации, который учитывает линейное сопротивление. Поскольку это неравномерное уравнение, решение состоит из двух частей. qx — общее решение для равномерного уравнения. q2 является частным решением неоднородного уравнения. Общее решение однородного уравнения удовлетворяет уравнению для собственных колебаний с линейным сопротивлением.

Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. Людмила Фирмаль

Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2 .

В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e

q. Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение Людмила Фирмаль

Таким образом, это движение не может быть вибрацией, но называется его собственным движением или вибрацией. Частное решение неоднородного уравнения q2 называется вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой q, равной сумме qt и q2, где q = qt + q2 величина q называется общим вынужденным движением (или вынужденной вибрацией). Общее решение qt для однородного дифференциального уравнения q1 + 2nql + k2qi = 0 может быть выражено в одной из следующих трех форм в зависимости от соотношения между величинами n и k. n k, ql = e «‘(cie’ ^ r2 ‘+ C2e

В любом из этих случаев qt стремится к нулю с течением времени, то есть затухает из-за наличия коэффициентов e

Если коэффициент демпфирования мал (n A) движение не будет колебаться, поскольку затухание очень велико. Следовательно, если через некоторое время возникает линейное сопротивление, суммарное вынужденное движение

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальное уравнение вынужденных колебаний.

Предположим, что на колебательную систему все время дейст­вует вынуждающая сила, изменяющаяся со временем по гармони­ческому закону

где F₀ — амплитуда силы. Очевидно, вынуждающая сила изменя­ется со временем с периодом T = 2p/w. Она совершает работу, знак которой зависит от разности фаз между силой и скоростью движе­ния тела. Когда направления движения тела и вынуждающей силы совпадают, то она совершает положительную работу, ускоряя дви­жение колеблющегося тела. Если же направления движения тела и вынуждающей силы противоположны, то она совершает отрица­тельную работу, тормозя движение колеблющегося тела. С течени­ем времени это приводит к тому, что тело вынуждено совершать колебания с той же частотой, с какой изменяется вынуждающая сила.

В случае малых механических колебаний, когда сила сопротивления пропор­циональна скорости в соответствии со вторым законом динамики, уравнение движения имеет вид

, (70)

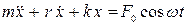
где (- kx) — возвращающая сила; (-r 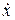) — сила сопротивления; F₀ cosw t -вынуждающая сила.

Учитывая, что w₀ 2 = k/m, d = r/(2m) и обозначив f_o = F / m,уравнение (70) можно переписать в виде:

(71)

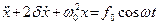
Это неоднородное дифференциальное уравнение второго порядка описывает вы­нужденные колебания в механической системе, например, колебания маятника. Решение его, как доказывается в курсе выс­шей математики, состоит из суммы x₁(t) — общего решения урав­нения (52) и x₂(t) — частного решения уравнения (71).

Решение уравнения (52) x₁(t), как установлено ранее,записывается в виде

где w = 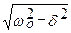, характеризует свободные, затухающие по экспоненциальному закону колебания, начальная амплитуда и фаза которых зависят от начальных условий. Эти колебания через не­которое время, называемое временем установления вынужденных колебании, практически исчезают. В установившемся режиме решение уравнения (71) ищем в виде:

где A — амплитуда вынужденных колебаний и j — сдвиг фаз между смещением и вынуждающей силой (в данном случае начальную фазу удобнее обозначать через — j). Их можно определить из условия, согласно которому подстановка выражения (73) в уравнение (71) должна приводить к тождеству. Тогда получим:

А = 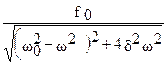(74)

tgj = 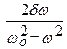(75)

Подставив в (73) значения A и j, определяемые формулами (74) и (75), получим частное решение (установившийся режим) неоднородного уравнения (71):

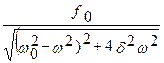
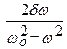
X = cos(w t — arctg ) (76)

Функция (76) в сумме с функцией (72) дает общее решение уравнения (71), описывающего поведение системы при вынужденных колебаниях. Таким образом, функция (76) описывает установив­шиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и обратно пропорциональна массе системы. Кроме того, амплиту­да установившихся вынужденных колебаний обратно пропорцио­нальна коэффициенту затухания d и уменьшается с его увеличе­нием.

Уравнение (71) и его решение (76) справедливо для вынужденных колебаний любой физической природы. Таким образом, общее дифференциальное уравнение вынужденных колебаний осциллятора, характеризуемого обобщённым параметром S, имеет вид:

(77)

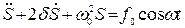
Если изменения какого-либо параметра системы описываются

дифференциальным уравнением (77), то в этот процесс представляет собой вынужденные колебания. Решение этого уравнения в установившемся режиме имеют вид аналогичный уравнениям (73) — (75).