Дифференциальное уравнение с гиперболическим косинусом

Гиперболические функции — sh, ch, th, cth, sech, csch

ОПРЕДЕЛЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ

ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ

ФОРМУЛЫ СЛОЖЕНИЯ

ch (x ± y) = ch x ch y ± sh x sh y

th(x ± y) = (th x ± th y)/(1 ± th x.th y)

cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)

ФОРМУЛЫ ДВОЙНЫХ УГЛОВ

sh 2x = 2 sh x ch x

ch 2x = ch 2 x + sh 2 x = 2 ch 2 x — 1 = 1 + 2 sh 2 x

th 2x = (2th x)/(1 + th 2 x)

ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ

$\text \frac <2>= \pm \sqrt <\frac<\textx — 1><2>>$ [+ если x > 0, — если x 0, — если x 3 x

ch 3x = 4 ch 3 x — 3 ch x

th 3x = (3 th x + th 3 x)/(1 + 3 th 2 x)

sh 4x = 8 sh 3 x ch x + 4 sh x ch x

ch 4x = 8 ch 4 x — 8 ch 2 x + 1

th 4x = (4 th x + 4 th 3 x)/(1 + 6 th 2 x + th 4 x)

СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

sh 3 x = ¼sh 3x — ¾sh x

ch 3 x = ¼ch 3x + ¾ch x

sh 4 x = 3/8 — ½ch 2x + 1/8ch 4x

ch 4 x = 3/8 + ½ch 2x + 1/8ch 4x

СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

sh x + sh y = 2 sh ½(x + y) ch ½(x — y)

sh x — sh y = 2 ch ½(x + y) sh ½(x — y)

ch x + ch y = 2 ch ½(x + y) ch ½(x — y)

ch x — ch y = 2 sh ½(x + y) sh ½(x — y)

sh x sh y = ½(ch (x + y) — ch (x — y))

ch x ch y = ½(ch (x + y) + ch (x — y))

sh x ch y = ½(sh (x + y) + sh (x — y))

ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ

В следующем мы принимаем, что x > 0. Если x -1 a называется обратным гиперболическим синусом of x. Аналогично определяются и другие обратные гиперболические функции. Обратные гиперболические функции являются многозначными, но в случае обратных тригонометрических функций мы ограничимся основными значениями, при которых их можно рассматривать как однозначные.

Ниже приведен список основных значений [если не указано иное] обратных гиперболических функций, выраженных через логарифмические функции, которые принимаются в качестве вещественных.

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Дифференциальное уравнение с гиперболическим косинусом

Кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной с обоих концов и находящейся под действием силы тяжести, называется цепной линией. Очевидно, цепная линия является плоской кривой, то есть такой кривой, все точки которой лежат в одной плоскости.

Долгое время считалось, что цепная линия представляет собой параболу, подобно тому, как траектория движения камня в поле земного тяготения есть парабола. Однако уже в начале 17 века великий итальянский мыслитель Галилео Галилей высказал предположения, что цепная линия не является параболой. Строгое решение задачи с выводом уравнения цепной линии впервые было найдено в трудах великих немецких мыслителей Готфрида Лейбница и Иоганна Бернулли, а также великого нидерландского естествоиспытателя Христиана Гюйгенса в 1691 году.

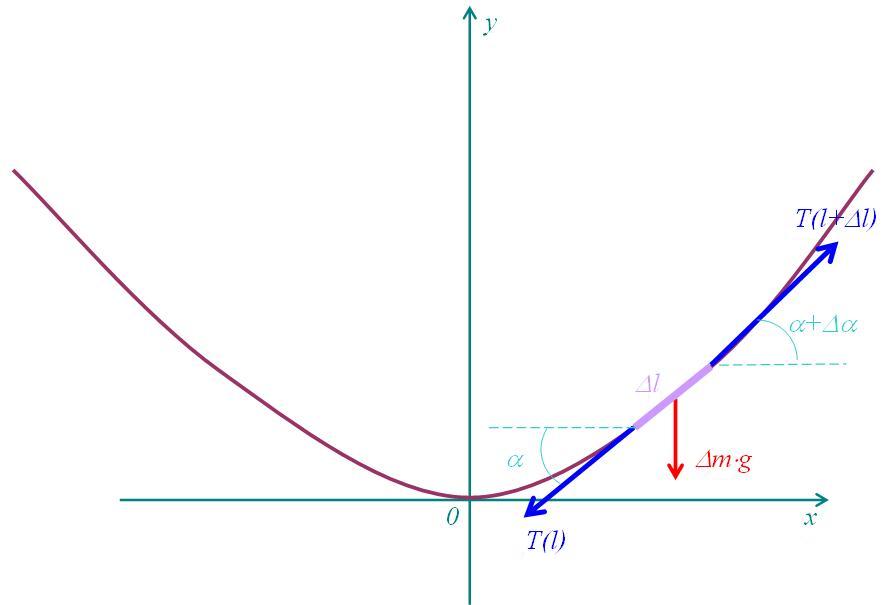
Рассмотрим элементарный участок нити длиной \(\Delta l\) (Рисунок 3). Масса этого участка равна \(\Delta m = \rho S \Delta l\) и на него действуют распределенная по длине сила тяжести интенсивности \(\rho gS\), направленная вниз и равная \(\Delta m g = \rho g S \Delta l\). Здесь \(\rho\) — объемная плотность материала нити, \(g\) — ускорение свободного падения, \(S\) — площадь поперечного сечения нити.

Также на концах данного участка действуют силы натяжения \(T(l)\) и \(T(l+\Delta l)\).

Рисунок 1. Цепи, используемые при штабелирование парахода “Бремен”. Фото из Федерального архива Германии.
Bundesarchiv Bild 102-06406, Bremen, Stapellauf des Dampfers «Bremen».

Рисунок 2. Цепи ограждения Царь-пушки в московском кремле. http://www.fotokonkurs.ru/photo/58515

Условие равновесия рассматриваемого участка запишется в виде: $$ \vec T(l) + \vec T(l+\Delta l) + \Delta m\vec g = 0. $$ В проекции на оси координат получим $$ — T(l)\cos(\alpha) + T(l+\Delta l)\cos(\alpha + \Delta \alpha) = 0. $$ $$ — T(l)\sin(\alpha) + T(l+\Delta l)\sin(\alpha + \Delta \alpha) — \rho gS\Delta l = 0.$$ Из первого уравнения получаем, что горизонтальная компонента силы натяжения \(T(l)\) всегда постоянна: \( T(l)\cos\alpha(l) = T_0 = const.\) Второе уравнение перепишем в виде: $$ d(T(l)\sin(\alpha(l)) = d(\rho gSl).$$ С учётом сказанного, можем записать $$ T_0 d(tg(\alpha(l)) = \rho gSdl).$$ Памятуя о геометрическом смысле производной, запишем \(tg\alpha = y’\) и тогда получим $$\frac

= \frac<\rho gS>.$$ Переходя к переменной x, используя правило дифференцирования сложной функции и выражение для дифференциала дуги кривой, получим $$\frac

= \frac \cdot \frac

= \frac \cdot \frac> = $$ $$ = \frac \cdot \frac <1><\sqrt<1+(y')^2>> = \frac <\rho gS>.$$ Отсюда, учитывая, что производная от первой производной есть вторая производная, получаем $$y» = \frac <\rho gS> \cdot \sqrt<1+(y')^2>.$$
Последнее уравнение называется дифференциальным уравнением цепной линии. Это уравнение второго порядка, допускающее понижение порядка. Чтобы понизить порядок уравнения сделаем замену \(z(x)=y’\). Тогда \(y»=z’\). Подставляя в последнее дифференциальное уравнение, получим $$\frac = z’ \frac <\rho gS> \cdot \sqrt<1+z^2>.$$

Рисунок 3. Ценная линия и расчётная схема.

Получили уравнение с разделяющимися переменными, которое после элементарных преобразований принимает вид $$\frac<\sqrt<1+z^2>> = \frac<\rho gS> \cdot dx.$$ Интегрируем последнее уравнение $$\int\frac<\sqrt<1+z^2>> = \frac<\rho gS> \int dx,$$ $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x + C_1.$$ Принимая за начало координат нижнюю точку цепной линии, заметим, что касательная в нижней точке горизонтальная, другими словами, нижняя точка является точкой экстремума для функции \(y(x)\). Следовательно, \(y’(0)=z(0)=0\). Подставим в последнее выражение \(x=0, y=0, z=0\). В результате получим \(С_1 = 0\). Тогда уравнение цепной линии перепишется в виде $$\ln|z + \sqrt<1+z^2>| = \frac<\rho gS> \cdot x.$$ Потенцируя полученное уравнение, перепишем его в показательной форме

Здесь для сокращения записи мы ввели обозначение \(\frac<\rho gS> = \kappa.\)
Умножим обе части уравнение (1) на выражение сопряжённое к левой части \(z-\sqrt<1+z^2>\). Получим $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = e^<\kappa x>\cdot(z — \sqrt<1+z^2>).$$ Нетрудно заметить, что $$(z + \sqrt<1+z^2>)\cdot(z — \sqrt<1+z^2>) = z^2 — (\sqrt<1+z^2>)^2 = z^2 -1 + z^2 = -1.$$ Вследствие последнего замечания, уравнение можно переписать в виде $$e^<\kappa x>\cdot(z — \sqrt<1+z^2>) = -1.$$ или в виде $$z — \sqrt <1+z^2>= -e^<\kappa x>. $$ Прибавим последнее выражением к выражению (1), и поделим полученное равенство на 2. В результате получим $$z = \frac — e^<-\kappa x>><2>. $$ Определение 1. Гиперболическим синусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac — e^<-x>><2>. $$ Определение 2. Гиперболическим косинусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac + e^<-x>><2>. $$ Предложение 1. Производная от гиперболического косинуса есть гиперболический синус, производная от гиперболического синуса есть гиперболический косинус, то есть$$sh'(x) = ch(x),$$ $$ch'(x) = sh(x).$$ Доказательство. $$sh'(x) = \left(\frac — e^<-x>><2>\right)’ = \frac <(e^— e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= ch(x);$$ $$ch'(x) = \left(\frac + e^<-x>><2>\right)’ = \frac <(e^+ e^<-x>)’> <2>= \frac <(e^)’ + (e^<-x>)’> <2>= \frac <(e^)’ — (e^<-x>)’> <2>= sh(x).$$ Доказательство завершено. ❑

Следствие 1. Первообразная от гиперболического косинуса есть гиперболический синус, а первообразная от гиперболического синуса есть гиперболический косинус.

Следствие 2. $$\int sh(x)dx = ch(x) + C, $$ $$ \int ch(x)dx = sh(x) + C.$$
С учётом сформулированных определений, а также памятуя о сделанной ранее замене \(z(x)\), перепишем выражение для прогиба в следующем виде $$ y’ = z = \frac — e^<-\kappa x>> <2>= sh(\kappa x).$$
На основании предложения 1 и следствий к нему, после интегрирования получим $$ y(x) = \int sh(\kappa x)dx = \frac <1> <\kappa>\cdot ch(\kappa x) + C.$$
В принятой системе координат, когда нижняя точка цепной линии является началом системы координат, справедливо следующее начальное условие \(y(0)=0\). Подставим это условие в найденное уравнение цепной линии и получим $$ y(0) = \frac <\kappa>+ C = 0,$$ $$ \frac <1> <\kappa>\cdot \frac <2>+C = \frac <1> <\kappa>\cdot \frac <1+1> <2>+C = \frac <1> <\kappa>+ C = 0. $$ Отсюда \(С=-\frac <1><\kappa>\) и уравнение цепной линии запишется в виде $$ y(x) = \frac <1> <\kappa>\left(ch(\kappa x) — 1\right).$$
Таким образом, форма цепной линии определяется как гиперболический косинус с параметром \(\kappa\). Кроме гиперболического синуса и гиперболического косинуса существуют также гиперболический тангенс и котангенс, которые определяются по тому же принципу, что и тригонометрический тангенс и котангенс, а именно:

Определение 3. Гиперболическим тангенсом от \(x\) называется функция, определённая следующим выражением $$th(x) = \frac .$$
Определение 4. Гиперболическим котангенсом от \(x\) называется функция, определённая как частное гиперболического скосинуса и гиперболического синуса. То есть гиперболический котангенс это функция, определённая следующим выражением $$cth(x) = \frac .$$
Из сделанных определений следуют равенства $$th(x) \cdot cth(x) = 1;$$ $$th(x) =\frac >>;$$ $$cth(x) =\frac >>.$$
Исследуем ряд других замечательных свойств гиперболических функций.

Предложение 2. Справедливы следующие тождества $$сh^2(x) — sh^2(x) = 1;$$ $$1-th^2(x) = \frac <1>,$$ $$cth^2(x) — 1 = \frac <1>.$$ Доказательство.

Из определений гиперболического косинуса и гиперболического синуса следует: $$ch^2(x) — sh^2(x) = \left(\frac + e^<-x>><2>\right)^2 — \left(\frac <(e^— e^<-x>)><2>\right)^2 = $$ $$ = \frac <(e^)^2 + 2e^xe^ <-x>+ (e^<-x>)^2> <4>— \frac <(e^)^2 — 2e^xe^ <-x>+ (e^<-x>)^2> <4>= e^xe^ <-x>= e^ = e^0 = 1.$$ Первое тождество доказано. Из него следует $$ch^2(x) = 1 + sh^2(x);$$ $$sh^2(x) = ch^2(x) — 1.$$ Тогда $$1 — th^2(x) = 1 — \frac = \frac = \frac <1>.$$ $$cth^2(x) — 1 = \frac — 1 = \frac = \frac <1>.$$ Все три тождества доказаны. ❑

Задание.
Найти производные гиперболического тангенса и гиперболического котангенса.

Решение.
По правилу дифференцирования частного, получим для производной гиперболического тангенса $$th'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = \frac <1>.$$
Аналогично получим производную для функции гиперболический котангенс $$cth'(x) = \left(\frac\right)’ = \frac = $$ $$ = \frac = \frac = — \frac <1>.$$
Таким образом, мы доказали следующие соотношения $$ th'(x) = \frac <1>;$$ $$ cth'(x) = — \frac <1>.$$
Обратим внимание на некоторое сходство полученных тождеств с соответствующими тригонометрическими тождествами.