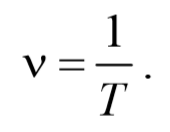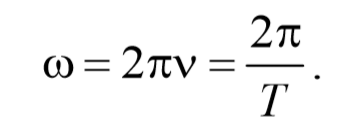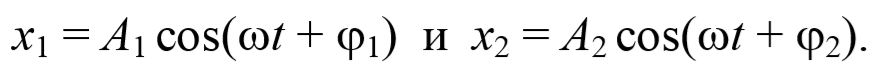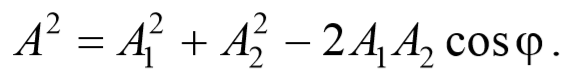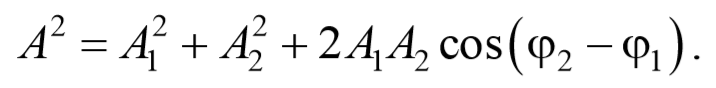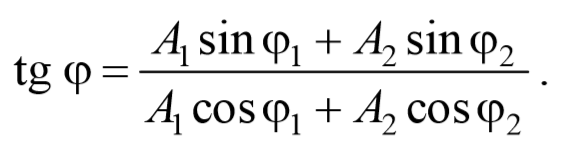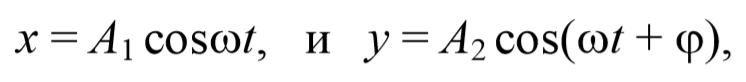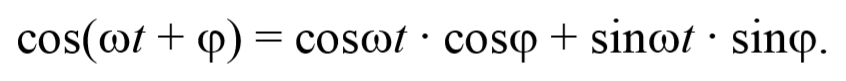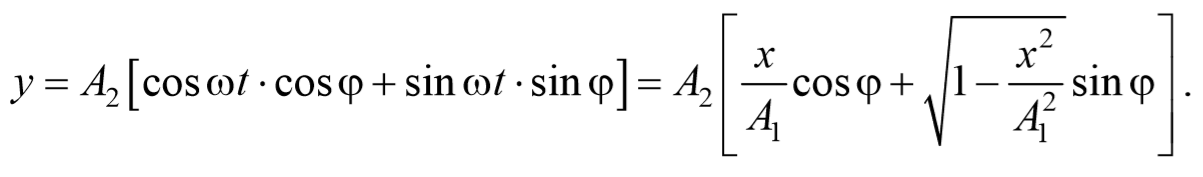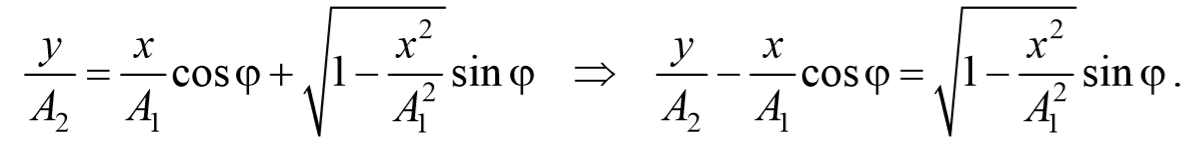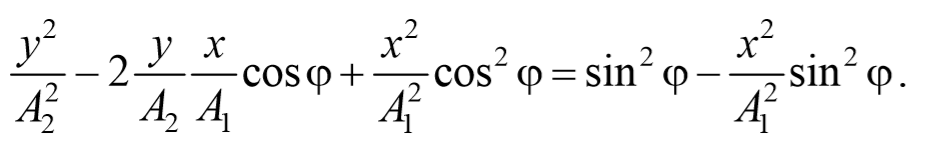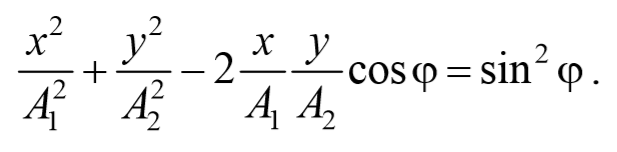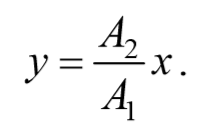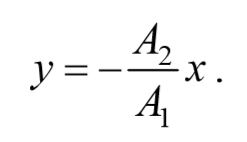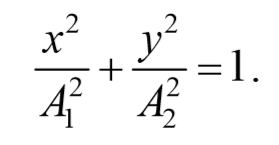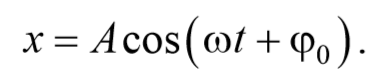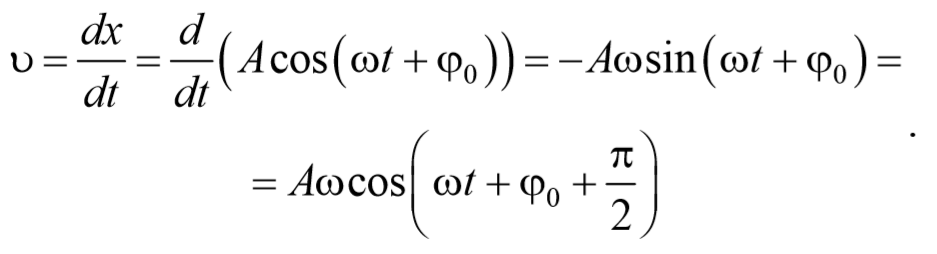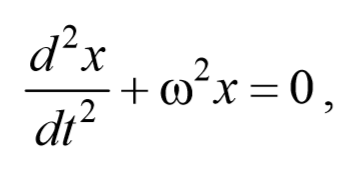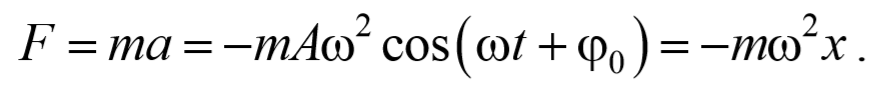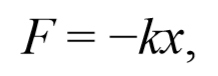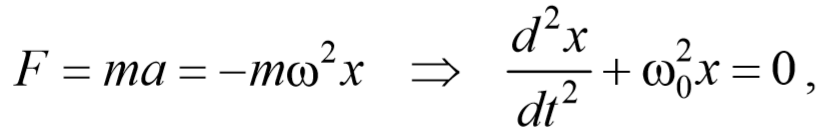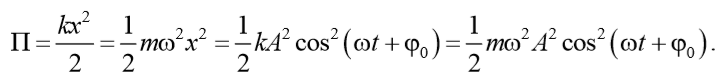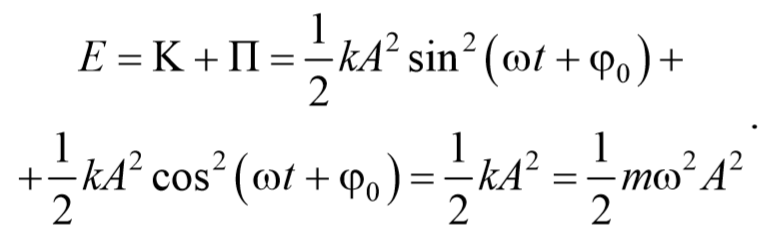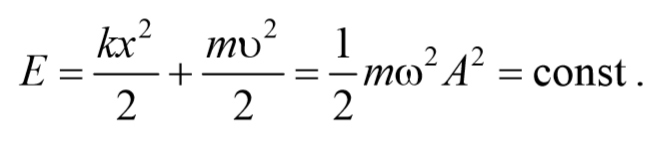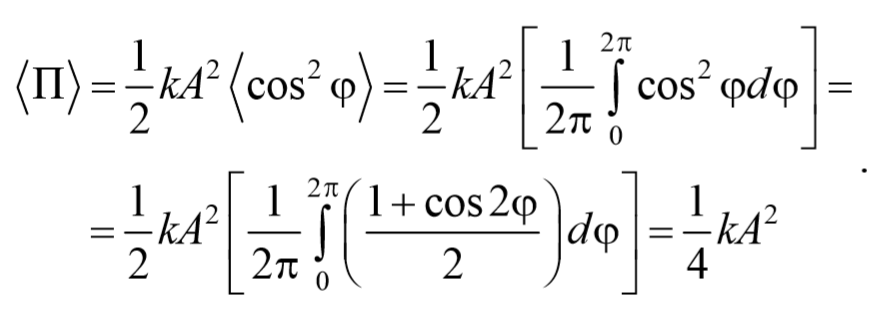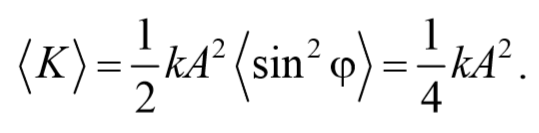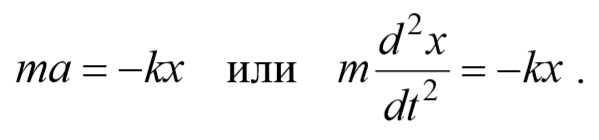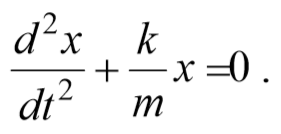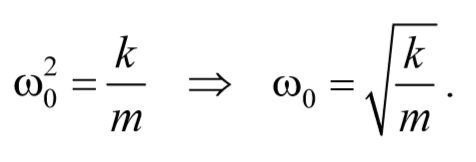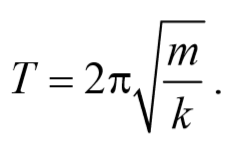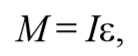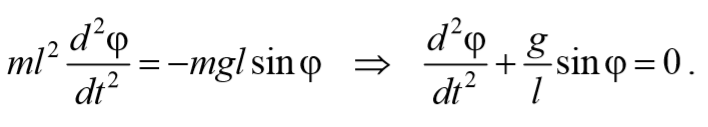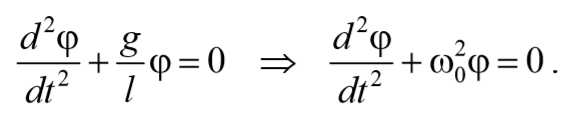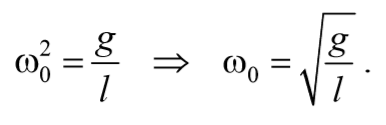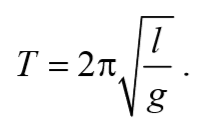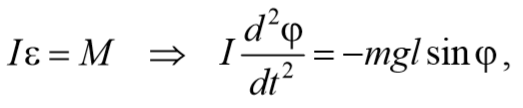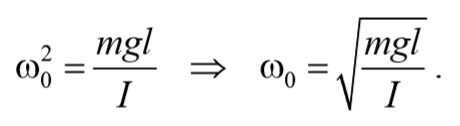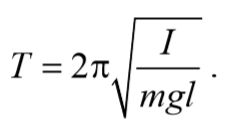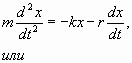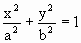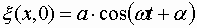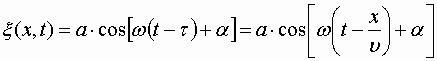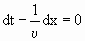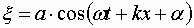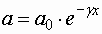Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.
Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид
1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.
2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.
3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .
За период система совершает одно полное колебание.
4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле
5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением
6) Фаза колебаний ωt + φ0 − фаза указывает местоположение колеблющейся точки в данный момент времени.
7) Начальная фаза φ0 − указывает местоположение колеблющейся точки в момент времени t = 0 .
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
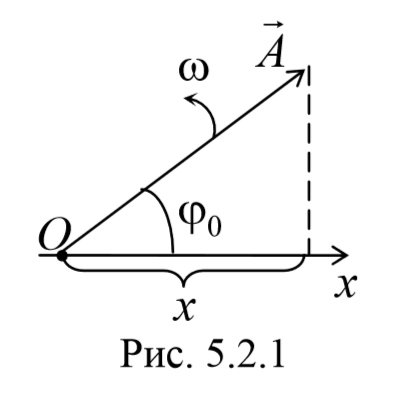
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ0 , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ0)
1. Сложение одинаково направленных гармонических колебаний.
Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x1 и x2 , которые запишутся следующим образом:
Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x2+x2 , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов
Так как угол между векторами А 1 и А 2 равен φ=π-(φ2-φ1) , то cos[π-(φ2-φ1)]=-cos(φ2-φ1) , следовательно, результирующая амплитуда колебания будет равна
Определим начальную фазу результирующего колебания.
Из рисунка видно, что начальная фаза результирующего колебания
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.
2. Сложение взаимно перпендикулярных гармонических колебаний.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид
где φ − разность фаз обоих колебаний.
Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$x\over A_1$$ , а sinωt= $$\sqrt<1-cos^2 ωt>=\sqrt<1-x^2\over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)
Перепишем это уравнение в следующем виде
После преобразования, получим
Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим
Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.
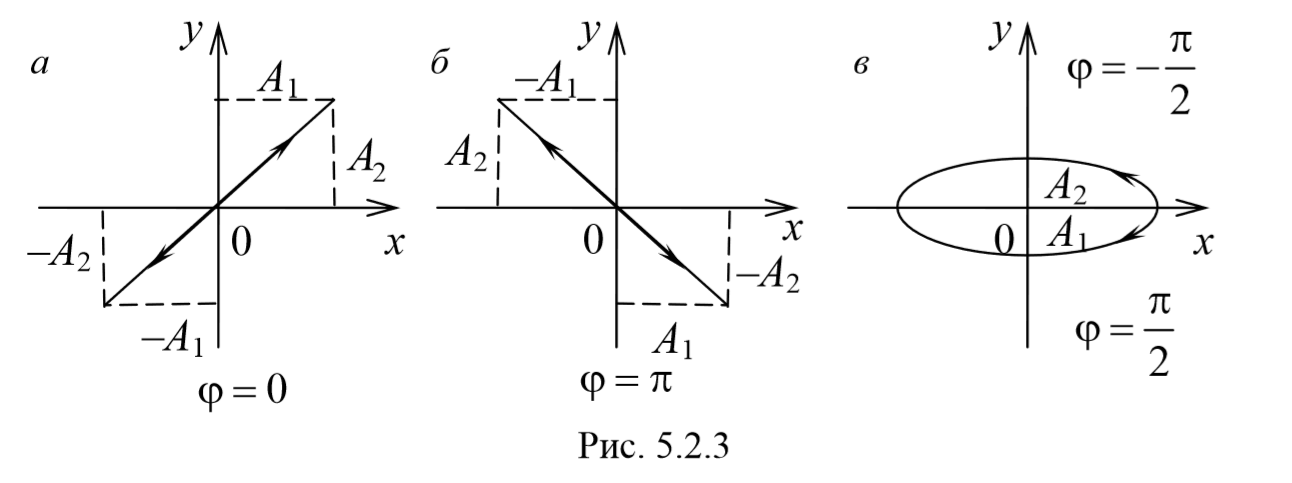
Рассмотрим несколько частных случаев и определим форму траектории для них:
a) разность фаз равна нулю [φ=0]
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= \sqrt
2) разность фаз равна ±π[φ=±π] .
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
3) Разность фаз равна ± $$π\over 2$$ [φ=± $$π \over2$$ ] . Тогда
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$π\over 2$$ и φ=- $$π\over 2$$ отличаются направлением движения. Если φ=+ $$π\over 2$$ , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=-A2sinωt и движение совершается по часовой стрелке. Если φ=- $$π\over 2$$ , , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=A2sinωt и движение совершается против часовой стрелке.
Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис
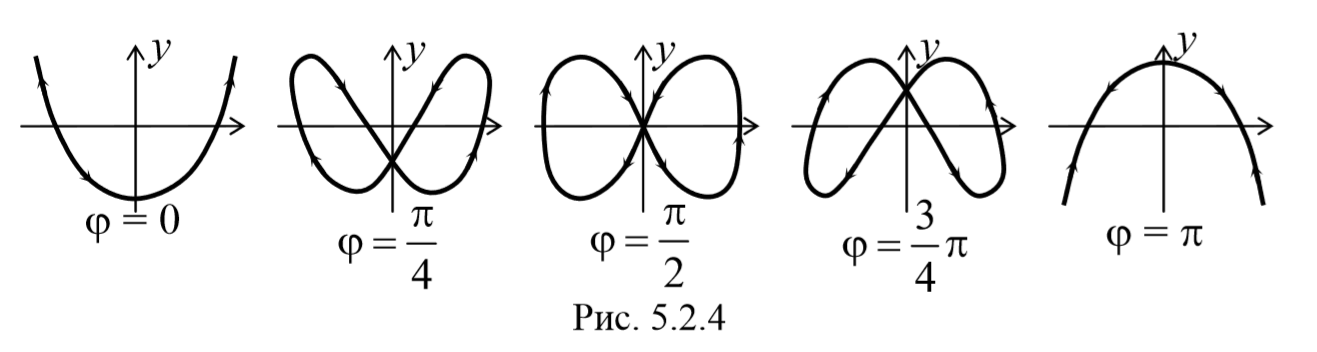
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.
На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.
По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
Продифференцируем по времени уравнение гармонических колебаний
и получим выражение для скорости
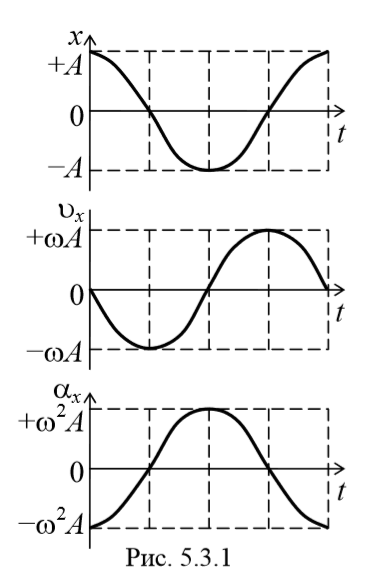
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .
Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).
Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний
Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы
Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,
где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .
Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением
ω0 − собственная частота осциллятора.
Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ0) .
5.4. Энергия гармонических колебаний.
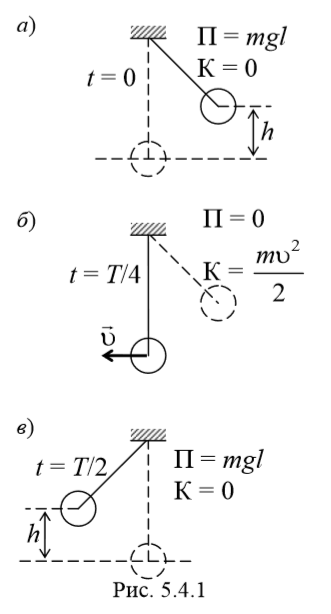
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
Кинетическая энергия тела, совершающего гармонические колебания равна
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
Следовательно, полная энергия гармонического колебания
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
Аналогично получается для среднего значение кинетической энергии
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2
5.5. Пружинный, математический и физический маятники.
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
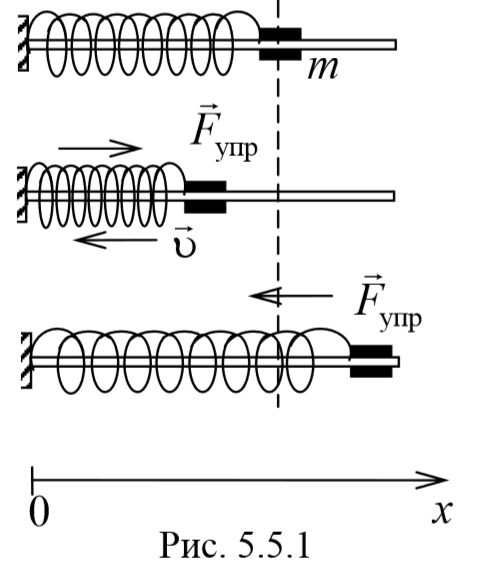
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox Fупр=ma . Упругая сила Fупр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
Так как период колебаний определяется по формуле T= $$2π\over ω_0$$ , то период колебаний пружинного маятника
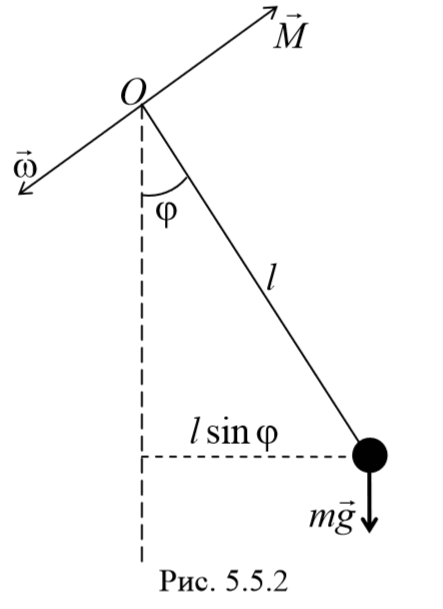
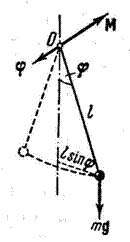
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.
При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения
где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φ\over dt^2$$ , получим
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
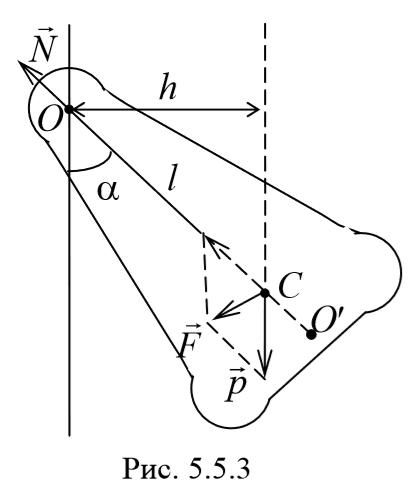
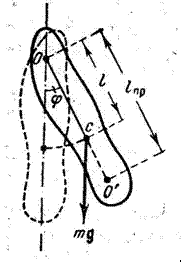
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .
Согласно основному уравнению динамики вращательного движения получаем
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$\sqrt
будет иметь такой же период колебаний, что и данный физический маятник.
Величина lпр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
Свободные и вынужденные механические колебания
Вы будете перенаправлены на Автор24
Движения или процессы, которые имеют определенную повторяемость, называют колебаниями.
Физическая природа колебаний может быть различной, в этой связи различают:
- механические колебания;
- электромагнитные колебания;
- квантовые;
- смешанные (электромеханические).
Разные по природе колебания описываю при помощи одинаковых параметров и одинаковых уравнений. Общим подходом исследования механических и электромагнитных колебаний пользовались разные ученые –физики, например, Д.У. Рэлеей и А.Г. Столетов, П.Н. Лебедев.
Свободные гармонические колебания
Колебания считают свободными (собственными) в том случае, если они выполняются только за счет энергии, которая была сообщена колебательной системе в начальный момент времени и далее внешние воздействия на эту систему отсутствуют.
Самым простым для математического описания видом колебательных процессов стали гармонические колебания.
Гармоническими колебаниями называют колебания, у которых изменение колеблющегося параметра происходит по закону синуса или косинуса:
$s=s_m cos (\omega_0 t+\varphi) (1),$
где $s_m$ — наибольшее значение переменного параметра $s$ (амплитуда); $\omega_0$ — циклическая частота колебаний; $\varphi$ — начальная фаза колебаний; $(\omega_0 t+\varphi)$ — фаза колебаний в момент времени $t$. $- s_m
Гармонические колебания рассматриваются подробно поскольку:
- колебания, которые происходят в реальной действительности часто близки к гармоническим;
- разные периодические процессы можно представлять как сумму гармонических колебаний.
Состояния колебательной системы, выполняющей гармонические колебания, повторяются спустя промежуток времени, который именуют периодом колебаний ($T$). За время, равное периоду, фаза колебаний изменяется на величину, равную $2\pi$:
Готовые работы на аналогичную тему
$(\omega_0 (t+T)+\varphi)=(\omega_0 t+\varphi)+2\pi (2)$,
в результате можем записать:
Величину, обратную периоду, называют частотой колебаний:
Частота – это физическая величина, равная количеству полных колебаний которое система совершает за единицу времени. При этом выполняется равенство:
$\omega_0 = 2\pi \nu (5).$
Дифференциальные уравнения свободных гармонических колебаний
Поведем дифференцирование по времени выражения (1), тогда первая производная равна:
$\frac
Вторая производная по времени от (1):
$\frac
В выражении (6) мы получили скорость колебаний, в (7) ускорение. Данные параметры движения колеблются с той же циклической частотой и амплитудами равными:
$v_m=s_m \omega_0$; $a_m= s_m \omega_0^2$.
Из формулы (6) мы видим, что фаза скорости отлична от фазы смещения $s$ на $\frac<\pi><2>$, тогда как фаза ускорения смещена на $\pi$. Это означает то, что в тот момент времени, когда смещение равно нулю ($s=0$), скорость наибольшая. Если $s$ максимально и отрицательно, то ускорение имеет наибольшую положительную величину.
Из выражений (1) и (7) легко сделать вывод о том, что дифференциальное уравнение свободных гармонических колебаний записывается в виде:
Решением данного уравнения служит $s(t)$ вида (1).
Затухающие колебания
В реальной действительности любые свободные колебания являются затухающими.
Колебания называют затухающими, если их амплитуда в результате энергетических потерь с течением времени уменьшается.
Самым простым механизмом уменьшения энергии в колебательной системе является ее трансформация в тепловую энергию, в результате наличия сил трения.
Формула, которая описывает затухание колебаний, определена свойствами системы, выполняющей движения.
Дифференциальное уравнение свободных затухающих колебаний линейной системы можно представить в виде:
где $\delta$ — коэффициент затухания; $\omega_0$ — круговая частота свободных незатухающих колебаний этой же колебательной системы (если $\delta =0$) называется собственной частотой.
Если затухание колебаний мало ($\delta^2 \ll \omega_0^2$), то решением дифференциального уравнения (9) является функция вида:
$s=s_0 e^ <-\delta t>\cos (\omega t +\varphi) (10),$
где $\omega = \omega_0^2-\delta^2$; $s_0=s_m e^<-\delta t>$ — амплитуда колебаний при их затухании ($s_m $- начальная амплитуда).
Строго говоря, затухающие колебания нельзя отнести к периодическим. К ним нельзя применять понятия:
Иногда при очень малом затухании понятие период используют для обозначения отрезка времени между парой соседних максимумов (минимумов) параметра колебания. В этом случае период затухающих колебаний вычисляют как:
Конечным результатом эволюции колебательной системы с затухающими колебаниями является стремление ее к состоянию равновесия. Данное поведение понятно, поскольку связано с потерей энергетического запаса на совершение работы против сил трения в механической системе.
Вынужденные колебания
Вынужденными называют колебания, если на колебательную систему происходит периодическое воздействие внешней силы (имеется источник энергии).
Вынужденными механическими колебаниями можно назвать звуковую волну, которая распространяется в веществе при наличии источника звука.
Для получения в реальной системе незатухающих колебаний, следует компенсировать потери энергии. Данная компенсация возможна при действии, например, периодического фактора $X(t)$, который изменяется в соответствии с законом:
$X(t)=X_0 \cos (\omega t)(12).$
При механических колебаниях вместо $X(t)$ можно записать внешнюю вынуждающую силу:
$F=F_0 \cos (\omega t) (13).$
Рассмотрим колебания тела на упругой пружине. Уравнением его колебаний будет:
где $r$ — коэффициент сопротивления; $\omega_0 = \sqrt<\frac
Уравнения вынужденных колебаний с учетом (13) запишем в виде:
$m \ddot < x>=-kx-r\dot
$\ddot
Уравнение (17) — это линейное неоднородное дифференциальное уравнение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 05 2021
Дифференциальное уравнение свободных гармонических колебаний
Простейшими из колебаний являются гармонические. Это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
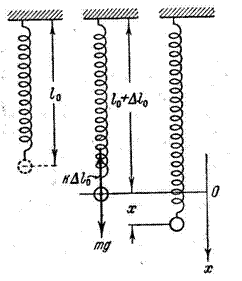
Рассмотрим пружинный маятник (Рис. 1.7.1).
Рис. 1.7.1. Пружинный маятник
В состоянии покоя сила тяжести уравновешивается упругой силой:
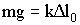 | (1.7.1) |
Если сместить шарик от положения равновесия на расстояние х, то удлинение пружины станет равным Δl0 + х. Тогда результирующая сила примет значение:
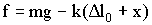 | (1.7.2) |
Учитывая условие равновесия (1.7.1), получим:
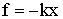 | (1.7.3) |
Знак «минус» показывает, что смещение и сила имеют противоположные направления.
Упругая сила f обладает следующими свойствами:
- Она пропорциональна смещению шарика из положения равновесия;
- Она всегда направлена к положению равновесия.
Для того, чтобы сообщить системе смещение х, нужно совершить против упругой силы работу:
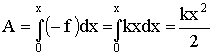 | (1.7.4) |
Эта работа идет на создание запаса потенциальной энергии системы:
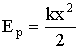 | (1.7.5) |
Под действием упругой силы шарик будет двигаться к положению равновесия со все возрастающей скоростью 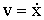
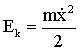
Уравнение второго закона Ньютона в этом случае имеет вид:
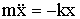 | (1.7.6) |
Преобразуем уравнение так:
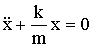 | (1.7.7) |
Вводя обозначение 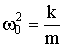
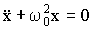 | (1.7.8) |
Прямой подстановкой легко убедиться, что общее решение уравнения (1.7.8) имеет вид:
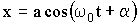 | (1.7.9) |
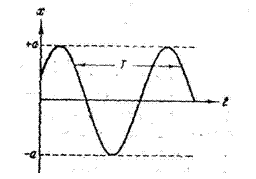
где а — амплитуда и φ — начальная фаза колебания — постоянные величины. Следовательно, колебание пружинного маятника является гармоническим (Рис. 1.7.2).
Рис. 1.7.2. Гармоническое колебание
Вследствие периодичности косинуса различные состояния колебательной системы повторяются через определенный промежуток времени (период колебаний) Т, за который фаза колебания получает приращение 2π. Рассчитать период можно с помощью равенства:
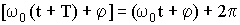 | (1.7.10) |
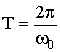 | (1.7.11) |
Число колебаний в единицу времени называется частотой:
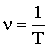 | (1.7.12) |
За единицу частоты принимается частота такого колебания, период которого равен 1 с. Такую единицу называют 1 Гц.
Из (1.7.11) следует, что:
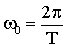 | (1.7.13) |
Следовательно, ω0 — это число колебаний, совершаемое за 2π секунд. Величину ω0 называют круговой или циклической частотой. Используя (1.7.12) и (1.7.13), запишем:
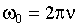 | (1.7.14) |
Дифференцируя (1.7.9) по времени, получим выражение для скорости шарика:
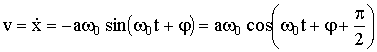 | (1.7.15) |
Из (1.7.15) следует, что скорость также изменяется по гармоническому закону и опережает смещение по фазе на ½π. Дифференцируя (1.7.15), получим ускорение:
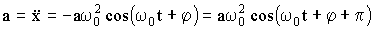 | (1.7.16) |
1.7.2. Математический маятник
Математическим маятником называют идеализированную систему, состоящую из нерастяжимой невесомой нити, на которой подвешено тело, вся масса которого сосредоточена в одной точке.
Отклонение маятника от положения равновесия характеризуют углом φ, образованным нитью с вертикалью (Рис. 1.7.3).
Рис. 1.7.3. Математический маятник
При отклонении маятника от положения равновесия возникает вращательный момент, который стремится вернуть маятник в положение равновесия:
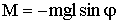 | (1.7.17) |
Напишем для маятника уравнение динамики вращательного движения, учитывая, что момент его инерции равен ml 2 :
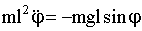 | (1.7.18) |
Это уравнение можно привести к виду:
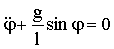 | (1.7.19) |
Ограничиваясь случаем малых колебаний sinφ ≈ φ и вводя обозначение:
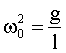 | (1.7.20) |
уравнение (1.7.19) может быть представлено так:
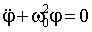 | (1.7.21) |
что совпадает по форме с уравнением колебаний пружинного маятника. Следовательно, его решением будет гармоническое колебание:
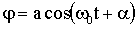 | (1.7.22) |
Из (1.7.20) следует, что циклическая частота колебаний математического маятника зависит от его длины и ускорения свободного падения. Используя формулу для периода колебаний (1.7.11) и (1.7.20), получим известное соотношение:
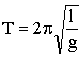 | (1.7.23) |
1.7.3. Физический маятник
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с центром инерции. В положении равновесия центр инерции маятника С находится под точкой подвеса О на одной с ней вертикали (Рис. 1.7.4).
Рис. 1.7.4. Физический маятник
При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, который стремится вернуть маятник в положение равновесия:
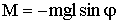 | (1.7.24) |
где m — масса маятника, l — расстояние между точкой подвеса и центром инерции маятника.
Напишем для маятника уравнение динамики вращательного движения, учитывая, что момент его инерции равен I:
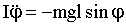 | (1.7.25) |
Для малых колебаний sinφ ≈ φ. Тогда, вводя обозначение:
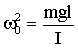 | (1.7.26) |
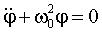 | (1.7.27) |
что также совпадает по форме с уравнением колебаний пружинного маятника. Из уравнений (1.7.27) и (1.7.26) следует, что при малых отклонениях физического маятника от положения равновесия он совершает гармоническое колебание, частота которого зависит от массы маятника, момента инерции и расстояния между осью вращения и центром инерции. С помощью (1.7.26) можно вычислить период колебаний:
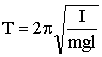 | (1.7.28) |
Сравнивая формулы (1.7.28) и (1.7.23) получим, что математический маятник с длиной:
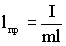 | (1.7.29) |
будет иметь такой же период колебаний, что и рассмотренный физический маятник. Величину (1.7.29) называют приведенной длиной физического маятника. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штайнера момент инерции физического маятника равен:
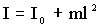 | (1.7.30) |
где I0 — момент инерции относительно центра инерции. Подставляя (1.7.30) в (1.7.29), получим:
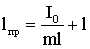 | (1.7.31) |
Следовательно, приведенная длина всегда больше расстояния между точкой подвеса и центром инерции маятника, так что точка подвеса и центр качания лежат по разные стороны от центра инерции.
1.7.4. Энергия гармонических колебаний
При гармоническом колебании происходит периодическое взаимное превращение кинетической энергии колеблющегося тела Ек и потенциальной энергии Еп, обусловленной действием квазиупругой силы. Из этих энергий слагается полная энергия Е колебательной системы:
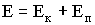 | (1.7.32) |
Распишем последнее выражение
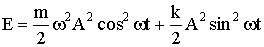 | (1.7.33) |
Но к = mω 2 , поэтому получим выражение для полной энергии колеблющегося тела
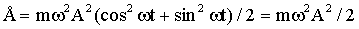 | (1.7.34) |
Таким образом полная энергия гармонического колебания постоянна и пропорциональна квадрату амплитуды и квадрату круговой частоты колебания.
1.7.5. Затухающие колебания .
При изучении гармонических колебаний не учитывались силы трения и сопротивления, которые существуют в реальных системах. Действие этих сил существенно изменяет характер движения, колебание становится затухающим .
Если в системе кроме квазиупругой силы действуют силы сопротивления среды (силы трения), то второй закон Ньютона можно записать так:
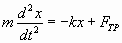 . . | (1.7.34.а) |
Для решения этого дифференциального уравнения необходимо знать, от каких параметров зависит сила трения. Обычно предполагают, что при не очень больших амплитудах и частотах сила трения пропорциональна скорости движения и, естественно, направлена противоположно ей:
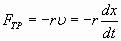 , , | (1.7.34.б) |
где r – коэффициент трения, характеризующий свойства среды оказывать сопротивление движению. Подставим (1.7.34б) в (1.7.34а):
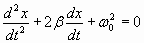 , , | (1.7.34.в) |
где 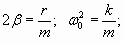
Решение уравнения(1.7.34.в) существенно зависит от знака разности: 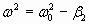
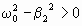
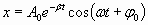 . . | (1.7.35) |
График этой функции показан на рис.1.7.5 сплошной кривой 1, а штриховой линией 2 изображено изменение амплитуды:
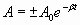 . . | (1.7.35.а) |
Период затухающих колебаний зависит от коэффициента трения и определяется формулой
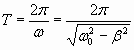 . . | (1.7.35.б) |
При очень малом трении 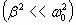
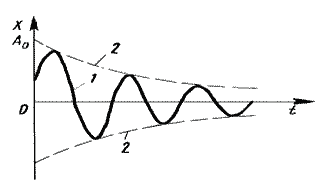 |  |
| Рис.1.7.5. Затухающее колебание | Рис.1.7.6. Апериодический процесс |
Быстрота убывания амплитуды колебаний определяется коэффициентом затухания : чем больше β, тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда. На практике, степень затухания часто характеризуют логарифмическим декрементом затухания , понимая под этим величину, равную натуральному логарифму отношения двух последовательных амплитуд колебаний, разделенных интервалом времени, равным периоду колебаний:
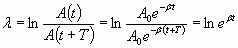
Следовательно, коэффициент затухания и логарифмический декремент затухания связаны достаточно простой зависимостью:
| λ=βT . | (1.7.37) |
При сильном затухании 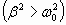
1.7.6. Вынужденные колебания. Резонанс .
Вынужденными колебаниями называются такие, которые возникают в системе при участии внешней силы, изменяющейся по периодическому закону.
Предположим, что на материальную точку кроме квазиупругой силы и силы трения действует внешняя вынуждающая сила
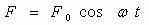
где F 0 – амплитуда; ω – круговая частота колебаний вынуждающей силы. Составим дифференциальное уравнение (второй закон Ньютона):
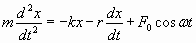
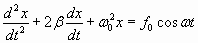 , , | (1.7.38) |
где 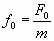
Решение дифференциального уравнения (3.19) является суммой двух колебаний: затухающих и незатухающих с амплитудой
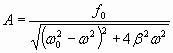 , , | (1.7.39) |
Амплитуда вынужденного колебания (1.7.39) прямо пропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от коэффициента затухания среды и круговых частот собственного и вынужденного колебания. Если ω 0 и β для системы заданы, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной .
Само явление – достижение максимальной амплитуды для заданных ω 0 и β – называют резонансом.
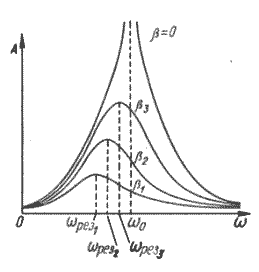 |
| Рис. 1.7.7. Резонанс |
При отсутствии сопротивления 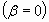
Механический резонанс может быть как полезным, так и вредным явлением. Вредное действие резонанса связано главным образом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать возможные возникновения резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют несколько собственных частот колебаний и соответственно несколько резонансных частот.
Если коэффициент затухания внутренних органов человека был бы не велик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, повреждению связок и т.п. Однако такие явления при умеренных внешних воздействиях практически не наблюдаются, так как коэффициент затухания биологических систем достаточно велик. Тем не менее резонансные явления при действии внешних механических колебаний происходят во внутренних органах. В этом, видимо, одна из причин отрицательного воздействия инфразвуковых колебаний и вибраций на организм человека.
1.7.7. Автоколебания
Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время.
Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями , а сами системы – автоколебательными.
Амплитуда и частота автоколебаний зависят от свойств в самой автоколебательной системе, в отличие от вынужденных колебаний они не определяются внешними воздействиями.
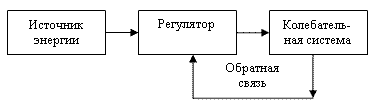 |
| Рис. 1.7.8. Блок-схема автоколебаний |
Во многих случаях автоколебательные системы можно представить тремя основными элементами (рис.1.7.8): 1) собственно колебательная система; 2) источник энергии; 3) регулятор поступления энергии в собственно колебательную систему. Колебательная система каналом обратной связи (рис. 6) воздействует на регулятор, информирую регулятор о состоянии этой системы.
Классическим примером механической автоколебательной системы являются часы, в которых маятник или баланс являются колебательной системой, пружина или поднятая гиря – источником энергии, а анкер – регулятором поступления энергии от источника в колебательную систему.
Многие биологические системы (сердце, легкие и др.) являются автоколебательными. Характерный пример электромагнитной автоколебательной системы – генераторы автоколебательных колебаний.
1.7.8. Сложение колебаний одного направления
Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты:
x 1 =a 1 cos(ω 0 t + α 1 ), x 2 =a 2 cos(ω 0 t + α 2 ).
Гармоническое колебание можно задать с помощью вектора, длина которого равна амплитуде колебаний, а направление образует с некоторой осью угол, равный начальной фазе колебаний. Если этот вектор вращается с угловой скоростью ω 0 , то его проекция на выбранную ось будет изменяться по гармоническому закону. Исходя из этого, выберем некоторую ось Х и представим колебания с помощью векторов а 1 и а 2 (рис.1.7.9).
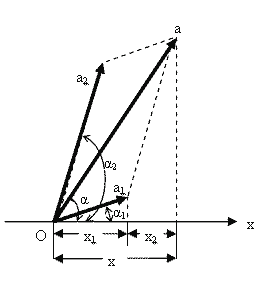 |
| Рис.1.7.9 |
Вектор а является суммой векторов а 1 и а 2 . Проекция вектора а на ось Х равна сумме проекций векторов а 1 и а 2 :
Следовательно, вектор а представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью, что и векторы а 1 и а 2 . Таким образом, результирующее движение представляет собой гармоническое колебание с частотой ω 0 , амплитудой а и начальной фазой α. Используя теорему косинусов, находим значение амплитуды результирующего колебания:
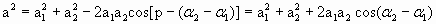 | (1.7.40) |
Из рис.1.7.6 следует, что
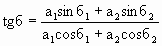
Схемы, в которых колебания изображаются графически в виде векторов на плоскости, называются векторными диаграммами.
Из формулы 1.7.40 следует. Что если разность фаз обоих колебаний равна нулю, амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний. Если разность фаз складываемых колебаний равна 
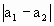
1.7.9. Биения
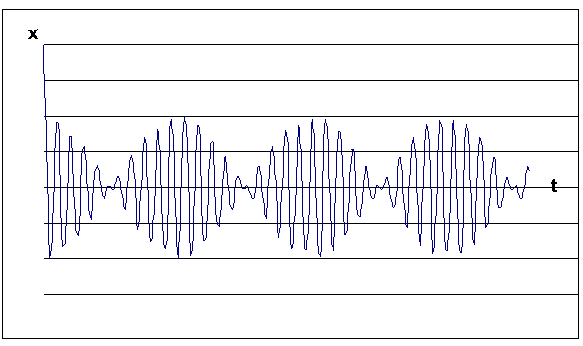
Рассмотрим сложение двух гармонических колебаний одинакового направления мало отличающихся по частоте. Пусть частота одного из них равна ω , а второго ω+∆ω, причем ∆ω 1 =a cos ωt, x 2 =a cos(ω+∆ω)t.
Сложив эти выражения и используя формулу для суммы косинусов, получаем:
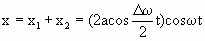 | (1.7.41) |
(во втором множителе пренебрегаем членом 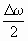
 |
| Рис.1.7.10 |
Колебания (1.7.41) можно рассматривать как гармоническое колебание частотой ω, амплитуда которого изменяется по закону 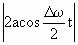
1.7.10. Сложение взаимно перпендикулярных колебаний (фигуры Лиссажу)
Если материальная точка совершает колебания как вдоль оси х, так и вдоль оси у, то она будет двигаться по некоторой криволинейной траектории. Пусть частота колебаний одинакова и начальная фаза первого колебания равна нулю, тогда уравнения колебаний запишем в виде:
| х=а cos ωt, y=b cos(ωt+α), | (1.7.42) |
где α – разность фаз обоих колебаний.
Выражение (1.7.42) представляет заданное в параметрическом виде уравнение траектории, по которой движется точка, участвующая в обоих колебаниях. Если исключить из уравнений (1.7.42) параметр t, то получим уравнение траектории в обычном виде:
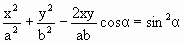 | (1.7.43) |
Уравнение (1.7.43) представляет собой уравнение эллипса, оси которого ориентированы произвольно относительно координатных осей х и у. Ориентация эллипса и величина его полуосей зависят от амплитуд а и b и разности фаз α. Рассмотрим некоторые частные случаи:
α=mπ (m=0, ±1, ±2, …). В этом случае эллипс вырождается в отрезок прямой
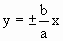 , , | (1.7.44) |
где знак плюс соответствует нулю и четным значениям m (рис 1.7.8.а), а знак минус – нечетным значениям m (рис.1.7.8.б). Результирующее колебание является гармоническим с частотой ω, амплитудой 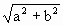
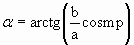
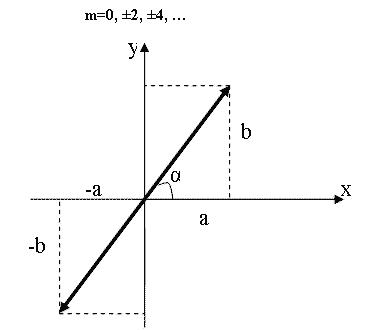 |
| Рис.1.7.11.а |
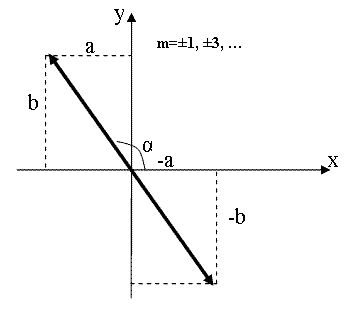 |
| Рис.1.7.11. б |
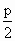
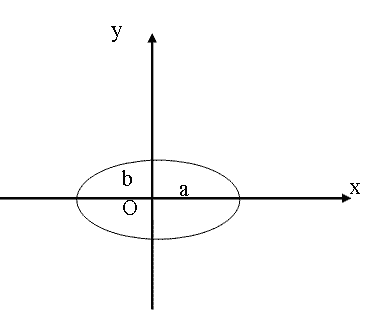
(m=0, ±1, ±2, …). В этом случае уравнение имеет вид
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны амплитудам (рис. 1.7.12). Если амплитуды равны, то эллипс становится окружностью.
 |
| Рис.1.7.12 |
Если частоты взаимно перпендикулярных колебаний отличаются на малую величину ∆ω, их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В этом случае уравнения колебаний можно записать
x=a cos ωt, y=b cos[ωt+(∆ωt+α)]
и выражение ∆ωt+α рассматривать как разность фаз, медленно изменяющуюся со временем по линейному закону. Результирующее движение в этом случае происходит по медленно изменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от -π до+π.
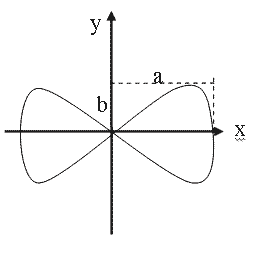
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу . Пусть, например, частоты складываемых колебаний относятся как 1 : 2 и разность фаз π/2. Тогда уравнения колебаний имеют вид
x=a cos ωt, y=b cos[2ωt+π/2].
За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться. Вид кривой показан на рис. 1.7.13. Кривая при таком же соотношении частот, но разности фаз равной нулю показана на рис.1.7.14. Отношение частот складываемых колебаний обратно отношению числа точек пересечения фигур Лиссажу с прямыми, параллельными осям координат. Следовательно, по виду фигур Лиссажу можно определить соотношение частот складываемых колебаний или неизвестную частоту. Если одна из частот известна.
 |
| Рис.1.7.13 |
 |
| Рис.1.7.14 |
Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее получающиеся фигуры Лиссажу.
1.7.11. Распространение волн в упругой среде
Если в каком-либо месте упругой (твёрдой жидкой или газообразной) среды возбудить колебания её частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью υ. процесс распространения колебаний в пространстве называется волной .
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия.
В зависимости от направлений колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волн. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновения только продольных волн. В твёрдой среде возможно возникновение как продольных, так и поперечных волн.
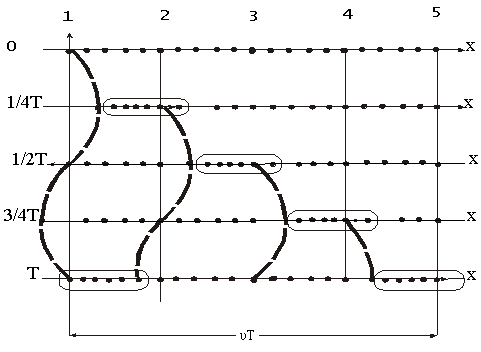
На рис. 1.7.12 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2 и т. д. обозначены частицы отстающие друг от друга на расстояние, равное (¼ υT), т.е. на расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами. В момент, времени принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положения равновесия частица 2. По пришествие ещё четверти периода первая часть будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигнет крайнего верхнего положения, а третья частица начнёт смещаться вверх из положения равновесия. В момент времени равный T, первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как чальный момент. Волна к моменту времени T, пройдя путь (υT), достигнет частицы 5.
На Рис. 1.7.13 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведения частиц в поперечной волне, могут быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево.
Из рисунка видно, что при распространении продольной волны в среде создаются чередующиеся сгущения и разряжения частиц (места сгущения обведены на рисунке пунктиром), перемещающиеся в направлении распространения волны со скоростью υ.
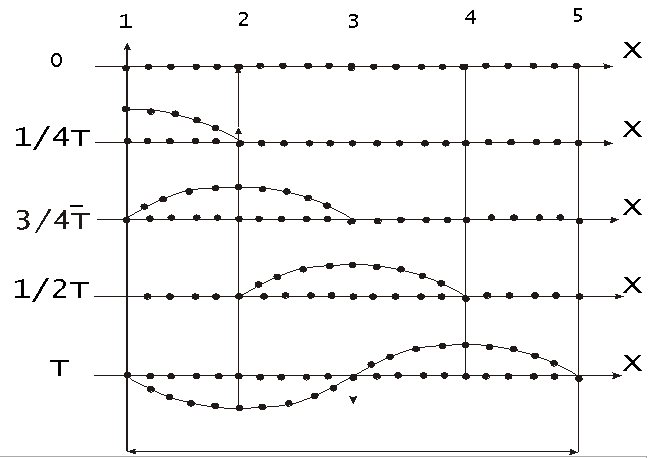 |
| Рис. 1.7.15 |
 |
| Рис. 1.7.16 |
На рис. 1.7.15 и 1.7.16 показаны колебания частиц, положения, равновесия которых лежат на оси x. В действительности колеблются не только частицы, расположенные вдоль оси x, а совокупность частиц, заключённых в некотором объёме. Распространяясь от источников колебаний, волновой процесс охватывает всё новые и новые части пространства, геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания ещё не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются не подвижными (они проходят через положения равновесия частиц, колеблющихся в одной фазе ). Волновой фронт всё время перемещается.
Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне – множество концентрических сфер.
 |
| Рис. 1.7.17 |
Пусть плоская волна распространяется вдоль оси x . Тогда все точки сферы, положения, равновесия которых имеет одинаковую координату x (но различие значения координат y и z), колеблются в одинаковой фазе.
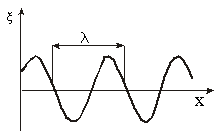
На Рис. 1.7.17 изображена кривая, которая даёт смещение ξ из положения равновесия точек с различными x в некоторый момент времени. Не следует воспринимать этот рисунок как зримое изображение волны. На рисунке показан график функций ξ ( x, t) для некоторого фиксированного момента времени t. Такой график можно строить как для продольной так и для поперечной волны.
Расстояние λ, на короткое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны . Очевидно, что
| λ=υT | (1.7.45 ) |
где υ – скорость волны, T – период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2π (см. рис. 1.7.14)
Заменив в соотношении(1.7.45) T через 1/ν (ν – частота колебаний), получим
| λν=υ . | (1.7.46) |
К этой формуле можно придти также из следующих соображений. За одну секунду источник волн совершает ν колебаний, порождая в среде при каждом колебании один «гребень» и одну «впадину» волны. К тому моменту, когда источник будет завершать ν — е колебание, первый «гребень» успеет пройти путь υ. Следовательно, ν «гребней» и «впадин» волны должны уложиться в длине υ.
1.7.12. Уравнение плоской волны
Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t :
(имеются в виду координаты равновесного положения частицы). Эта функция должна быть периодической относительно времени t , и относительно координат x, y, z. . Периодичность по времени вытекает из того, что точки, отстоящие друг от друга на расстоянии λ , колеблются одинаковым образом.
Найдем вид функции ξ в случае плоской волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение ξ будет зависеть только от x и t :
 |
| Рис.1.7.18 |
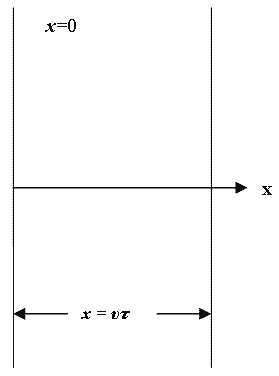
Пусть колебания точек, лежащих в плоскости x = 0 (рис. 1.7.18), имеют вид
Найдем вид колебания точек в плоскости, соответствующей произвольному значению x . Для того, чтобы пройти путь от плоскости x =0 до этой плоскости, волне требуется время 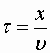
Итак, уравнение плоской волны (продольной, и поперечной), распространяющейся в направлении оси x , выглядит следующим образом:
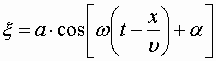 | (1.7.47) |
Величина а представляет собой амплитуду волны. Начальная фаза волны α определяется выбором начала отсчета x и t . При рассмотрении одной волны начало отсчета времени и координаты обычно выбирают так, чтобы α была равной нулю. При совместном рассмотрении нескольких волн сделать так, чтобы для всех них начальные фазы равнялись нулю, как правило, не удается.
Зафиксируем какое – либо значение фазы, стоящей в уравнении (1.7.47), положив
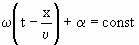 | (1.7.48) |
Это выражение определяет связь между временем t и тем местом x , в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx/dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (1.7.48), получим
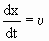 . . | (1.7.49) |
Таким образом, скорость распространения волны υ уравнении (1.7.47) есть скорость перемещения фазы, в связи с чем, ее называют фазовой скоростью.
Согласно (1.7.49) dx/dt> 0, следовательно, уравнение (1.7.47) описывает волну, распространяющуюся в сторону возрастания x .
Волна, распространяющаяся в противоположном направлении, описывается уравнением
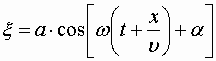 | (1.7.50) |
Действительно, приравняв константе фазу волны (1.7.50) и продифференцировав получившееся равенство, придем к соотношению
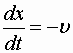
из которого следует, что волна (1.7.50) распространяется в сторону убывания x .
Уравнению плоской волны можно придать симметричный относительно x и t вид. Для этого введем величину
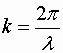 , , | (1.7.51) |
которая называется волновым числом. Умножив числитель и знаменатель последнего выражения на частоту ν, и вспомнив, что 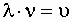
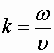 . . | (1.7.52) |
Раскрыв в уравнении волны
круглые скобки и используя волновое число, придем к следующему уравнению плоской волны, распространяющейся вдоль оси :
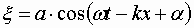 | (1.7.53) |
Уравнение волны, распространяющейся в сторону убывания x :
При выводе формулы (1.7.53) мы предполагали, что амплитуда колебаний не зависит от x . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается – наблюдается затухание волны. Опыт показывает, что в однородной среде такое затухание происходит по экспоненциальному закону:
Соответственно уравнение плоской волны, с учетом затухания , имеет следующий вид:
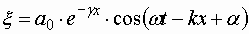 | (1.7.54) |
(a 0 – амплитуда в точках плоскости x = 0).
© ФГОУ ВПО Красноярский государственный аграрный университет, 2013
http://spravochnick.ru/fizika/mehanicheskie_kolebaniya_i_volny/svobodnye_i_vynuzhdennye_mehanicheskie_kolebaniya/
http://www.kgau.ru/distance/2013/et4/001/01_07.htm