Дифференциальное уравнение теплопроводности для шара

Теплопроводность через сферическую оболочку

Объектом исследования является сферическая оболочка заданной толщины с переменным коэффициентом теплопроводности и с заданными значениями температуры на внутренней и внешней поверхностях оболочки.

Цель проекта — определить распределение температуры внутри оболочки.

В процессе работы выведено дифференциальное уравнение теплопроводности применительно к данным конкретным условиям задачи и получено решение этого уравнения в виде функции T(r), где T — температура в произвольной точке оболочки а r — расстояние между этой точкой и геометрическим центром оболочки. Разработана программа TSO, рассчитывающая функцию T(r) и строящая её график для различных задаваемых пользователем параметров задачи.

Результатом исследования является аналитическое решение уравнения теплопроводности T(r) и графическая иллюстрация этого решения, изображаемая на экране компьютера программой TSO.

Полученная в проекте функция T(r) и разработанная программа TSO могут быть полезными для разработчиков химических и ядерных реакторов, котлов тепловых станций и различных сосудов в области промышленной и бытовой техники.

Курсовой проект выполнен в текстовом редакторе Microsoft WORD 7.0.

В учении о теплообмене рассматриваются процессы распространения теплоты в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений.

Перенос теплоты может осуществляться тремя способами: теплопроводностью, конвекцией и излучением, или радиацией. Эти формы глубоко различны по своей природе и характеризуются различными законами.

Процесс переноса теплоты теплопроводностью происходит между непосредственно соприкасающимися телами или частицами тел с различной температурой. Учение о теплопроводности однородных и изотропных тел опирается на весьма прочный теоретический фундамент. Оно основано на простых количественных законах и располагает хорошо разработанным математическим аппаратом. Теплопроводность представляет собой, согласно взглядам современной физики, молекулярный процесс передачи теплоты.

Известно, что при нагревании тела кинетическая энергия его молекул возрастает. Частицы более нагретой части тела, сталкиваясь при своем беспорядочном движении с соседними частицами, сообщают им часть своей кинетической энергии. Этот процесс постепенно распространяется по всему телу. Перенос теплоты теплопроводностью зависит от физических свойств тела, от его геометрических размерах, а также от разности температур между различными частями тела. При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворительно не решены. Эти трудности состоят в том, что тепловые процессы развиваются в неоднородной среде, свойства которой зависят от температуры и изменяются по объему; кроме того, трудности возникают с увеличением сложности конфигурации системы.

Целью данного курсового проекта является нахождение закона распределения температуры в веществе, которым заполнено пространство между двумя сферами.

2 Основные положения теплопроводности

2.1 Температурное поле

Теплопроводность представляет собой процесс распространения энергии между частицами тела, находящимися друг с другом в соприкосновении и имеющими различные температуры.

Рассмотрим нагрев какого-либо однородного и изотропного тела. Изотропным называют тело, обладающее одинаковыми физическими свойствами по всем направлениям. При нагреве такого тела температура его в различных точках изменяется во времени и теплота распространяется от точек с более высокой температурой к точкам с более низкой. Из этого следует, что в общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры Tкак в пространстве, так и во времени:

,———(2.1)

где — координаты точки;

Эта функция определяет температурное поле в рассматриваемом теле. В математической физике температурным полем называют совокупность значений температуры в данный момент времени для всех точек изучаемого пространства, в котором протекает процесс.

Если температура тела есть функция координат и времени, то температурное поле называют нестационарным, т. е. зависящим от времени:

.———(2.2)

Такое поле отвечает неустановившемуся тепловому режиму теплопроводности.

Если температура тела есть функция только координат и не изменяется с течением времени, то температурное поле тела называют стационарным:

.———(2.3)

Уравнения двухмерного температурного поля для режима стационарного:

;———(2.4)

.———(2.5)

На практике встречаются задачи, когда температура тела является функцией одной координаты, тогда уравнения одномерного температурного поля для режима стационарного:

;—-(2.6)

.—-(2.7)

Одномерной, например, является задача о переносе теплоты в стенке, у которой длину и ширину можно считать бесконечно большой по сравнению с толщиной.

2.2 Градиент температуры

Если соединить точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Изотермические поверхности между собой никогда не пересекаются. Они либо замыкаются на себя, либо кончаются на границах тела.

Рассмотрим две близкие изотермические поверхности с температурами T и T + Δ T(рисунок 2.1).

Перемещаясь из какой либо точки А, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться по изотермической поверхности, то изменения температуры не обнаружим. Если же перемещаться вдоль какого-либо направления P, то наблюдаем изменение температуры. Наибольшая разность температур на единицу длины будет в направлении нормали к изотермической поверхности. Предел отношения изменения температуры к расстоянию между изотермами по нормали , когда стремится к нулю, называют градиентом температуры.

———(2.8)

Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный частной производной от температуры по этому направлению. За положительное направление градиента принимается направление возрастания температур.

2.3 Основной закон теплопроводности

Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.

Связь между количеством теплоты , проходящим за промежуток времени через элементарную площадку dS, расположенную на изотермической поверхности, и градиентом температуры устанавливается гипотезой Фурье, согласно которой

.—-(2.9)

Минус в правой части показывает, что в направлении теплового потока температура убывает и grad T является величиной отрицательной. Коэффициент пропорциональности называется коэффициентом теплопроводности или более кратко — теплопроводностью. Справедливость гипотезы Фурье подтверждено многочисленными опытными данными, поэтому эта гипотеза в настоящее время носит название основного уравнения теплопроводности или закона Фурье.

Отношение количества теплоты, проходящего через заданную поверхность, ко времени называют тепловым потоком. Тепловой поток обозначают q и выражают в ваттах (Вт):

.———(2.10)

Отношение теплового потока dq через малый элемент изотермической поверхности к площади dS этой поверхности называют поверхностной плотностью теплового потока (или вектором плотности теплового потока), обозначают j и выражают в ваттах на квадратный метр (Вт/м2):

.————(2.11)

Вектор плотности теплового потока направлен по нормали к изотермической поверхности в сторону убывания температуры. Векторы j и grad T лежат на одной прямой, но направлены в противоположные стороны.

Тепловой поток q, прошедший сквозь произвольную поверхность S, находят из выражения

.———(2.12)

Количество теплоты, прошедшее через эту поверхность в течение времени t, определяется интегралом

.———(2.13)

Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.

2.4 Дифференциальное уравнение теплопроводности

Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс. Для сложных процессов, к которым относится передача теплоты теплопроводностью, при установлении зависимостей между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса не во всем изучаемом пространстве, а в элементарном объеме вещества в течение бесконечно малого отрезка времени. Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается дифференциальным уравнением теплопроводности. В пределах выбранного элементарного объема и бесконечно малого отрезка времени становится возможным пренебречь изменением некоторых величин, характеризующих процесс.

При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:

внутренние источники теплоты отсутствуют;

среда, в которой распространяется тепло, однородна и изотропна;

используется закон сохранения энергии, который для данного случая формулируется так: разность между количеством теплоты, вошедшей вследствие теплопроводности в элементарный параллелепипед за время dt и вышедшей из него за тоже время, расходуется на изменение внутренней энергии рассматриваемого элементарного объема.

Выделим в среде элементарный параллелепипед с ребрами (рисунок 2.2). Температуры граней различны, поэтому через параллелепипед проходит теплота в направлении осей . Через площадку за время dt, согласно уравнению Фурье, проходит количество теплоты:

———(2.14)

(grad T взят в виде частной производной, т. к. предполагается зависимость температуры не только от x, но и от других координат и времени).

Через противоположную грань на расстоянии dz отводится количество теплоты, определяемое из выражения:

,———(2.15)

где — температура второй грани, а величина определяет изменение температуры в направлении z.

Последнее уравнение можно представить в другом виде:

.—-(2.16)

Итак, приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси z равно:

.———(2.17)

Приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси y выразится аналогичным уравнением:

,———(2.18)

а в направлении оси x:

.———(2.19)

Полное приращение внутренней энергии в параллелепипеде:

.—-(2.20)

С другой стороны, согласно закону сохранения энергии:

,———(2.21)

где — объем параллелепипеда;

— масса параллелепипеда;

c — удельная теплоемкость среды;

— плотность среды;

— изменение температуры в данной точке среды за время dt.

Левые части уравнения (2.20) и (2.21) равны, поэтому:

,—-(2.22)

.———(2.23)

Величину называют оператором Лапласа и обычно обозначают сокращенно ; величину называют температуропроводностью и обозначают буквой a. При указанных обозначениях дифференциальное уравнение теплопроводности принимает вид:

.———(2.24)

Уравнение (2.24) называется дифференциальным уравнением теплопроводности (или дифференциальным уравнением Фурье) для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Оно является основным при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью и устанавливает связь между временным и пространственным изменениям температуры в любой точке поля.

Температуропроводность является физическим параметром вещества и имеет единицу м2/c. В нестационарных тепловых процессах a характеризует скорость изменения температуры.

Из уравнения (2.24) следует, что изменение температуры во времени для любой точки тела пропорционально величине a. Поэтому при одинаковых условиях быстрее увеличивается температура у того тела, которое имеет большую температуропроводность.

Дифференциальное уравнение теплопроводности с источником теплоты внутри тела имеет вид:

,———(2.25)

гдеqV — удельная мощность источника, то есть количество выделяемой теплоты в единице объёма вещества в единицу времени.

Это уравнение записано в декартовых координатах. В других координатах оператор Лапласа имеет иной вид, поэтому меняется и вид уравнения. Например, в цилиндрических координатах дифференциальное уравнение теплопроводности с внутренним источником теплоты таково:

,—-(2.26)

гдеr — радиус-вектор в цилиндрической системе координат;

— полярный угол.

2.5 Краевые условия

Полученное дифференциальное уравнение Фурье описывает явления передачи теплоты теплопроводностью в самом общем виде. Для того чтобы применить его к конкретному случаю, необходимо знать распределение температур в теле или начальные условия. Кроме того, должны быть известны:

геометрическая форма и размеры тела,

физические параметры среды и тела,

граничные условия, характеризующие распределение температур на поверхности тела, или взаимодействие изучаемого тела с окружающей средой.

Все эти частные особенности совместно с дифференциальным уравнением дают полное описание конкретного процесса теплопроводности и называются условиями однозначности или краевыми условиями.

Обычно начальные условия распределения температуры задаются для момента времени t = 0.

Граничные условия могут быть заданы тремя способами.

Граничное условие первого рода задается распределением температуры на поверхности тела для любого момента времени.

Граничное условие второго рода задается поверхностной плотностью теплового потока в каждой точке поверхности тела для любого момента времени.

Граничное условие третьего рода задается температурой среды, окружающей тело, и законом теплоотдачи между поверхность тела и окружающей средой.

Решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить температурное поле во всем объеме тела для любого момента времени или найти функцию .

2.6 Теплопроводность через шаровую стенку

С учётом описанной в разделах 2.1 — 2.5 терминологии задачу данной курсовой работы можно сформулировать так. Постоянный тепловой поток направлен через шаровую стенку, причем источником теплоты является внутренняя сфера радиусом R1. Мощность источника P постоянна. Среда между граничными сферами изотропна, поэтому её теплопроводность χ является функцией одной переменной — расстояния от центра сфер (радиуса) r. По условию задачи . Вследствие этого температура среды тоже является в данном случае функцией одной переменной — радиуса r: T = T(r), а изотермические поверхности это концентрические сферы. Таким образом искомое температурное поле — стационарное и одномерное, а граничные условия являются условиями первого рода: T(R1) = T1, T(R2) = T2.

Из одномерности температурного поля следует, что плотность теплового потока j так же, как теплопроводность и температура, являются в данном случае функциями одной переменной — радиуса r. Неизвестные функции j(r) и T(r) можно определить одним из двух способов: или решать дифференциальное уравнение Фурье (2.25), или использовать закон Фурье (2.11). В данной работе избран второй способ. Закон Фурье для исследуемого одномерного сферически симметричного температурного поля имеет вид:

.————(2.27)

В этом уравнении учтено, что вектор нормали к изотермической поверхности n параллелен радиус-вектору r. Поэтому производная может быть записана как.

Определим зависимость плотности теплового потока j от r. Для этого сначала вычислим тепловой поток q через сферу произвольного радиуса r > R.

.————(2.28)

В частности, тепловой поток q1 через внутреннюю сферу радиусом R1 и тепловой поток q2 через наружную сферу радиусом R2 равны

———(2.29)

Все эти три потока создаются одним и тем же источником мощностью P. Поэтому все они равны P и поэтому равны между собой.

.————(2.30)

С учётом (2.28) и (2.29) это равенство можно записать в виде:

.———(2.31)

,———

получаем искомую зависимость плотности теплового потока j от радиуса r:

,————(2.32)

где C1 — это константа, определяемая формулой

.———(2.33)

Физический смысл полученного результата достаточно ясен: это известный закон обратных квадратов, характерный для задач со сферической симметрией.

Теперь, так как функция j(r) известна, можно рассматривать уравнение (2.27) как дифференциальное уравнение относительно функции T(r). Решение этого уравнение и даст искомое распределение температур. Подставив в (2.27) выражение (2.32) и заданную функцию , получим следующее дифференциальное уравнение:

.————(2.34)

Данное уравнение решается методом разделения переменных:

.————

Интегрирование этого выражения даёт:

———

Итак, функция T(r) имеет вид:

.———(2.35)

Константы C1 и C2 можно определить из граничных условий T(R1) = T1,
T(R2) = T2. Подстановка этих условий в (2.35) даёт линейную систему двух уравнений с двумя неизвестными C1 и C2:

.———(2.36)

Вычитая из первого уравнения второе, получим уравнение относительно C1:

,———

.———(2.37)

С учётом этого выражение (2.35) можно записать в виде:

.———(2.38)

Теперь первое граничное условие T(R1) = T1 даёт:

,———(2.39)

откуда следует выражение для константы C2:

.———(2.40)

Подстановка (2.40) в (2.39) даёт окончательное выражение для искомой функцииT(r):

.———(2.41)

Зная функцию T(r), можно из закона Фурье

————

определить и окончательное выражение для плотности теплового потока j как функции от радиуса r:

. ———(2.42)

Интересно отметить, что распределение температур не зависит от коэффициента b, но зато плотность потока пропорциональна b.

В результате проделанной работы выведено дифференциальное уравнение теплопроводности применительно к данным конкретным условиям задачи и получено решение этого уравнения в виде функции T(r). Разработана программа TSO, рассчитывающая функцию T(r) и строящая её график для различных задаваемых пользователем параметров задачи.

Дифференциальное уравнение теплопроводности

В учебниках по теплопередаче, в том числе и в [1], приводится вывод дифференциального уравнения температурного поля движущейся жидкости, уравнение энергии

(1.12)

где с_р, Дж/(кг×К) – изобарная теплоемкость; r, кг/м 3 – плотность; l, Вт/(м×К) – коэффициент теплопроводности; w_х, w_y, w_z – проекции вектора скорости движения жидкости; q_v , Вт/м 3 – объемная плотность внутреннего тепловыделения жидкости.

Уравнение (1.12) записано для случая l=const.

Дифференциальное уравнение температурного поля для твердых тел называется дифференциальным уравнением теплопроводности и может быть получено из (1.12) при условии w_х= w_y= w_z=0, с_р= с_v=с:

где — коэффициент температуропроводности, характеризует скорость изменения температуры в теле. Значения а = f (t) для различных тел приводятся в справочниках.

Дифференциальное уравнение теплопроводности

(1.13)

описывает нестационарное температурное поле твердых тел с внутренним тепловыделением (с внутренними источниками тепла). Такими источниками тепла могут быть: джоулева теплота, выделяемая при прохождении электрического тока по проводникам; теплота, выделяемая ТВЭЛами ядерных реакторов и т.д.

Дифференциальное уравнение теплопроводности (1.13), записанное в декартовых координатах, можно представить в цилиндрических (r, z, φ) и сферических (r, φ, ψ).

В частности, в цилиндрических координатах (r –радиус; φ – полярный угол; z — аппликата) дифференциальное уравнение теплопроводности имеет вид

(1.14)

Условия однозначности

Дифференциальное уравнение описывает множество процессов теплопроводности. Чтобы выделить из этого множества конкретный процесс, необходимо сформулировать особенности этого процесса, которые называются условиями однозначности и включают в себя:

· геометрические условия, характеризующие форму и размеры тела;

· физические условия, характеризующие свойства участвующих в теплообмене тел;

· граничные условия, характеризующие условия протекания процесса на границе тела;

· начальные условия, характеризующие начальное состояние системы при нестационарных процессах.

При решении задач теплопроводности различают:

· граничные условия первого рода, когда задается распределение температуры на поверхности тела:

· граничные условия второго рода, когда задается плотность теплового потока на поверхности тела:

· граничные условия третьего рода, когда задается температура среды t_ж и коэффициент теплоотдачи между поверхностью и средой.

В соответствии с законом Ньютона-Рихмана тепловой поток, передаваемый с 1м 2 поверхности в среду с температурой t_ж,

В то же время этот тепловой поток подводится к 1м 2 поверхности из глубинных слоев тела теплопроводностью

Тогда уравнение теплового баланса для поверхности тела запишется в виде

(1.15)

Уравнение (1.15) является математической формулировкой граничных условий третьего рода.

Система дифференциальных уравнений совместно с условиями однозначности представляет собой математическую формулировку задачи. Решения дифференциальных уравнений содержат константы интегрирования, которые определяются с помощью условий однозначности.

Контрольные вопросы и задания

1. Проанализируйте, какими способами передается теплота от горячей воды к воздуху через стенку батареи отопления: от воды к внутренней поверхности, через стенку, от наружной поверхности к воздуху.

2. Почему в правой части уравнения (1.3) стоит минус?

3. Проанализируйте с помощью справочной литературы зависимость λ(t) для металлов, сплавов, теплоизоляционных материалов, газов, жидкостей и ответьте на вопрос: как изменяется коэффициент теплопроводности с изменением температуры для этих материалов?

4. Как определяется тепловой поток (Q, Вт) при конвективной теплоотдаче, теплопроводности, тепловом излучении?

5. Запишите дифференциальное уравнение теплопроводности в декартовых координатах, описывающее трехмерное стационарное температурное поле без внутренних источников теплоты.

6. Запишите дифференциальное уравнение температурного поля проволоки, которая длительное время находится под напряжением при постоянной электрической нагрузке.

2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

2.1. Теплопроводность плоской стенки
при граничных условиях первого рода

Дано:плоская однородная стенка толщиной δ (рис. 2.1) с постоянным коэффициентом теплопроводности λ и постоянными температурами t₁ и t₂ на поверхностях.

Определить:уравнение температурного поля t=f (x) и плотность теплового потока q, Вт/м 2 .

Температурное поле стенки описывается дифференциальным уравнением теплопроводности (1.3) при следующих условиях:

· т. к. режим стационарный;

· т.к. отсутствуют внутренние источники теплоты;

· т.к. температуры t₁ и t₂ на поверхностях стенки постоянны.

Температура стенки является функцией только одной координаты х и уравнение (1.13) принимает вид

(2.1)

т.к. коэффициент температуропроводности стенки а ≠ 0.

Граничные условия первого рода:

при х=0 t= t₁ ,	(2.2)
при х= δ t= t₂.	(2.3)

Выражения (2.1), (2.2), (2.3) являются математической постановкой задачи, решение которой позволит получить искомое уравнение температурного поля t= f (x).

Интегрирование уравнения (2.1) дает

При повторном интегрировании получим решение дифференциального уравнения в виде

t=с₁х+с₂.

(2.4)

Из уравнения (2.4) при условии (2.2) получим

а при условии (2.3)

Подстановка констант интегрирования с₁ и с₂ в уравнение (2.4) дает уравнение температурного поля

(2.5)

по которому можно рассчитать температуру по толщине стенки на любой координате 0 2 ; t₂, t₃.

При стационарном режиме и постоянных температурах поверхностей стенки тепловой поток, передаваемый через трехслойную стенку, можно представить системой уравнений:

	(2.8)
	(2.9)
	(2.10)

(2.11)

Сложив левые и правые части уравнений (2.11), получим расчетную формулу для плотности теплового потока, передаваемого через трехслойную стенку

(2.12)

Температуры на границах слоев t₂ и t₃ можно рассчитать по уравнениям (2.8) – (2.10) после того, как найдена плотность теплового потока (q) по (2.12).

Общий вид уравнения (2.12) для многослойной плоской стенки, состоящей из п однородных слоев с постоянными температурами на наружных поверхностях 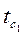и , имеет вид

(2.13)

Средний коэффициент теплопроводности многослойной стенки называют эффективным (λ_эф). Он равен коэффициенту теплопроводности однородной стенки, толщина и термическое сопротивление которой равны толщине и термическому сопротивлению многослойной стенки

(2.14)

2.2. Теплопроводность цилиндрической стенки
при граничных условиях первого рода

Дано:Однородная цилиндрическая стенка (стенка трубы) с внутренним радиусом r₁, наружным – r₂, длиной , с постоянным коэффициентом теплопроводности λ, с постоянными температурами на поверхностях t₁ и t₂.
(рис. 2.3).

Определить: уравнение температурного поля
t = f (r), тепловой поток, передаваемый через стенку
Q, Вт.

Дифференциальное уравнение теплопроводности в цилиндрических координатах (1.14) для условий данной задачи:

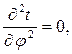
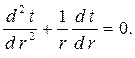(2.15)

Граничные условия первого рода:

при r=r₁ t=t₁ ,	(2.16)
при r=r₂ t=t₂ .	(2.17)

Порядок решения системы уравнений (2.15) – (2.17) тот же, что и в случае плоской стенки: находится общий интеграл дифференциального уравнения второго порядка (2.15), который содержит две константы интегрирования
с₁ и с₂ . Последние определяются с помощью граничных условий (2.16) и (2.17) и после подстановки их значений в решение дифференциального уравнения (общий интеграл) получаем уравнение температурного поля цилиндрической стенки t = f (r) в виде

(2.18)

где r₁ r r₂ – текущий радиус.

Нетрудно убедиться, что при подстановке в (2.18) r= r₁ получим t=t₁ , при r=r₂ получим t=t₂. Распределение температуры по толщине цилиндрической стенки, в соответствии с (2.18) подчиняется логарифмическому закону (рис. 2.3).

Для определения теплового потока воспользуемся законом Фурье:

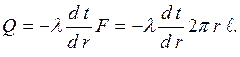(2.19)

Если взять производную от правой части уравнения (2.18) и подставить в (2.19), получим расчетную формулу для теплового потока цилиндрической стенки

(2.20)

В технических расчетах часто тепловой поток вычисляется для 1 м длины трубы:

и называется линейной плотностью теплового потока.

Запишем уравнение (2.20) в виде

где – термическое сопротивление теплопроводности цилиндрической стенки.

Для трехслойной цилиндрической стенки (трубы, покрытой двумя слоями тепловой изоляции) с известными постоянными температурами поверхностей (t₁ и t₄), с известными геометрическими размерами (r₁ , r₂, r₃, r₄ , ) и коэффициентами теплопроводности слоев (λ₁, λ₂, λ₃) (рис. 2.4) можно записать следующие уравнения для теплового потока Q:

(2.21)

Совместное решение системы уравнений (2.21) дает расчетную формулу для теплового потока, передаваемого через трехслойную стенку при заданных температурах на поверхностях,

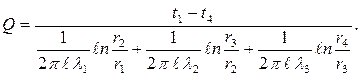(2.22)

Температуры на границах слоев (t₂, t₃) можно рассчитать по уравнениям (2.21).

Для многослойной цилиндрической стенки, состоящей из п слоев, формулу (2.22) можно записать в общем виде

(2.23)

Эффективный коэффициент теплопроводности для многослойной цилиндрической стенки, как и для многослойной плоской стенки, определяется из равенства суммы термических сопротивлений многослойной стенки термическому сопротивлению однородной стенки той же толщины, что и многослойная. Так, для двухслойной тепловой изоляции трубы
(рис. 2.4) эффективный коэффициент теплопроводности (λ_эф) определ ится из равенства

2.3. Теплопроводность плоской и цилиндрической стенок
при граничных условиях третьего рода (теплопередача)

Граничные условия третьего рода состоят в задании температуры жидкости (t_ж) и коэффициента теплоотдачи ( ) между поверхностью стенки и жидкостью.

Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей.

Примерами теплопередачи служит перенос теплоты от дымовых газов к воде через стенку трубы парового котла, перенос тепла от горячей воды к окружающему воздуху через стенку батареи отопления и т.д.

Теплообмен между поверхностью и средой (теплоносителем) может быть конвективным, если теплоноситель – жидкость (вода, нефть и т.д.) или радиационно-конвективным, когда теплота передается путем конвективного теплообмена и излучением, если теплоноситель – газ (дымовые газы, воздух и т.д.).

Рассмотрим теплопередачу через плоскую и цилиндрическую стенки при условии только конвективного теплообмена на поверхностях. Теплопередача с радиационно-конвективным теплообменом (сложным теплообменом) на поверхностях будет рассмотрена позже.

Плоская стенка(рис. 2.5)

Дано:

Плотность теплового потока q описывается следующими уравнениями в зависимости от способа передачи теплоты:

– от горячей жидкости к стенке

(2.24)

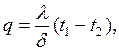(2.25)

– от стенки к холодной жидкости

(2.26)

Записав уравнения (2.24) – (2.26) в виде

(2.27)

и сложив почленно правые и левые части уравнений (2.27), получим формулу для расчета теплопередачи (q, Вт/м 2 ) через плоскую стенку в виде

(2.28)

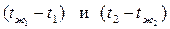
Величины называются термическими сопротивлениями теплоотдачи. Они прямо пропорциональны перепадам температур .

Температуры на поверхностях стенки t₁ и t₂ можно рассчитать по уравнениям (2.24) – (2.26) после того, как определена плотность теплового потока (q) по уравнению (2.28).

Формулу (2.28) можно записать в виде

(2.29)

где — коэффициент теплопередачи плоской стенки,характеризует интенсивность процесса теплопередачи.

Теплопередача через многослойную плоскую стенку рассчитывается по формуле

(2.30)

Цилиндрическая стенка(рис. 2.6)

Дано:

Для цилиндрической стенки, по аналогии с плоской стенкой, можно записать следующую систему уравнений:

	(2.31)
	(2.32)
	(2.33)

где — площади внутренней и наружной поверхностей трубы.

Записав уравнения (2.31) – (2.33) относительно разностей температур, а затем сложив правые и левые части уравнений, получим формулу для расчета теплопередачи (Q, Вт) через цилиндрическую стенку в виде

(2.34)

Температуры на поверхностях стенки t₁ и t₂ рассчитываются по уравнениям (2.31) – (2.33).

Формулу (2.34) также можно представить в виде

где – коэффициент теплопередачи цилиндрической стенки.

Для металлических труб с 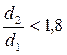можно пренебречь кривизной стенки и теплопередачу рассчитать по формулам для плоской стенки:

источники:

http://megaobuchalka.ru/8/46137.html