Дифференциальное уравнение теплопроводности в цилиндрической стенке

Теплопроводность при стационарном режиме

Теплопроводность при стационарном режиме

• В установившемся состоянии температурное поле T (x, yₜr, t) не зависит от времени. То есть,^ = 0.Дифференциальное уравнение теплопроводности (II-55)^ = aV2T (IV-I) DX is (П-56 И Р-57) Eh2du * Ldz2(IV-2)для решения конкретной задачи в Формулу (IV-2) необходимо добавить соответствующее граничное условие. Рассмотрим несколько простых случаев Определение стационарного температурного поля для объектов различной формы. § 1.

To рассмотрим теплопроводность тела плоская стенка неограниченная плоская стенка с подходящим температурным полем Его толщина равна 6, его поверхность параллельна плоскостям Y, z декартовой системы координат и находится при x = 0 и x = 6(рис. IV-1).Давайте поддержим его этими поверхностями Соответственно, задаются температуры 7 \и Т₂, то есть граничные условия типа 1(Глава 2,§ 5).

Выражение (IV-3) немедленно интегрируется. Людмила Фирмаль

Если Γ и T₂ не зависят от координат y и z, то, очевидно, искомое температурное поле Уравнение (IV-2), которое зависит от этих координат и определяет температуру T (x), принимает вид

= 0 (IV-3) dx2V ’при граничном условии. Г= 7 \ при x-0 (IV-4) T-X Tn-6.Общая форма решения T (x)=C₁X4-C₂,(1V-5).Где C. И C₂-произвольная константа, определяемая из граничного условия. (IV-4).фактически, если вы установите x = 0 в(IV-5)и используете первую формулу (IV-4), вы получите 2-е условие (IV-4) и (на основе) Л=С₂, (IV-6), x = 6. (IV-6) есть фига IV -!.

Теплопроводность плоской стенки т = С.6+С₂ = С.6+ 7 ′., (IV-7) где C = ^, 16 наконец, решение уравнения (IV-3) при граничном условии(1V-4) видно из (IV-8)(1V-8 T(x)линейно зависит от x, и эта зависимость T (x)= f (x)показана на рисунке вдоль толщины стенки. IV-1.Тепловой поток q можно определить по закону Фурье (1-3): q = — XgradГ, или В нашем случае, дифференцируя распределение температуры по толщине стенки (IV-8), мы видим, что dxowhence (IV-9) получается из Формулы (IV-9), которая равна 7′. > Flux тепловой поток положительный, то есть он направлен вдоль положительного направления оси X. В 7 \7 ′ 2 он направлен в противоположную сторону.

Этот результат является результатом второго закона термодинамики. В частности, тепло передается от нагретого тела к неотапливаемому. Количество тепла, проходящего через стенку за единицу времени, легко вычисляется с помощью (IV-9), q = ^ = X (T₁ — ^ 7′) 4 -/⁷. (1V-10) перепишите уравнение Фурье (P-54) в цилиндрической системе координат с цилиндрическим wall. To сделайте это, декартовы координаты и Цилиндрические координаты (рис. IV-2), x = r cos B, y = r sin B, z = R.

После проведения изменения этой переменной форма уравнения цилиндрической системы координат (P-54) равна dT / dTT- = а-э \ ДГ * \ _ ДТ Р ДГ \ &т р * ДВ. Рассмотрим 1D процесс стационарной теплопроводности на бесконечной цилиндрической стенке (рис. IV-3).Если на рисунке IV-2.Соотношение Прямоугольные и цилиндрические координаты T рис. 1в-3.Теплопроводность цилиндрической стенки, внутренней (r = r) и внешней (r-RJ) поверхности стенки.

Они не зависят от угла Вига, искомое температурное поле не зависит от этих переменных, и если оно стационарно, то уравнение (IV-11) имеет вид (FT (g) 1 dT ® Q dr-r dr (IV-12) при заданном граничном условии типа 1 R = r₁T =Г= = ₂ ₂t =t 決定 определяет распределение температуры по всей толщине стенки. Формула (IV-12) Переписывание (IV-13) (IV-14) Теперь 1 раз integration. As в результате после 2-го интеграла получаем общее решение уравнения. (IV-14): T(g)= CJn g 4-C₂. (IV-15) постоянная интеграция C! И С₂ должно быть определено из граничного условия(IV-13).Р= rxT₁=С₁1пг₁+С₂]и (IV-16)⁼ГГ2Т2⁷ ⁷1ПГ₂4″ С₂.

Если вы решите для (IV-16) относительно Ca, вы найдете первую интегральную константу Ca≥1n-и вторую константу Ca₂C = Tj-Cjlnr ^-br ^ linr ^ 1гг-ЛПП. ’1′ 1 замена Найдя значения Cb и C₂ в Формуле (IV-15), получим искомое распределение температуры по всей толщине цилиндрической стенки In-T ® =Tₗ+(T,-T₁) — I. (IV-17) ’ I следовательно T(g） Логарифмически зависит от радиусной координаты r. плотность теплового потока q определяется по закону Фурье. Основываясь на (IV-17), существует проходящее количество тепла.

Цилиндрическую стенку, которая указывает на единицу длины трубы, можно определить по формуле: Q-qF-q-2nr = inK (T1-T.). (IV-19) — — — в ri Q естественно не зависит от R. Тепло не будет накапливаться anywhere. By по аналогии с многослойной цилиндрической стенкой(1-6) принимается тепловое сопротивление многослойной цилиндрической стенки (рис. IV-4). Равна сумме тепловых сопротивлений отдельных слоев. На основе этого утверждения можно использовать формулу (IV-19) для создания формулы, определяющей количество тепла, которое проходит через нее.

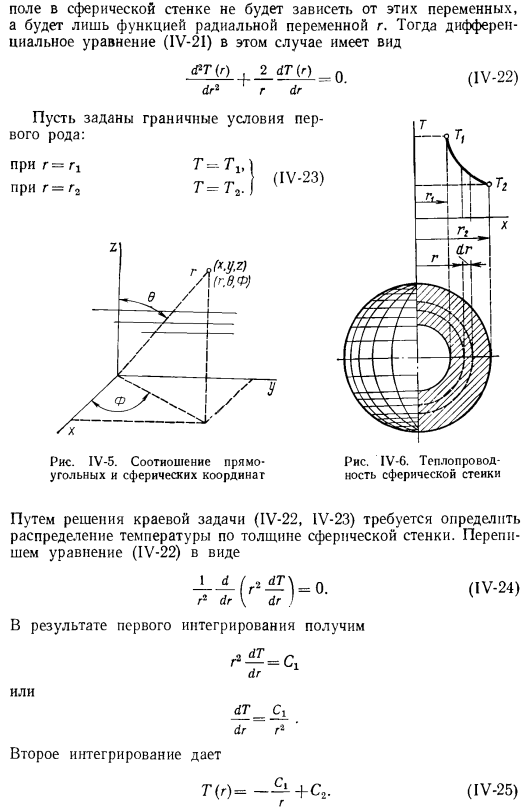
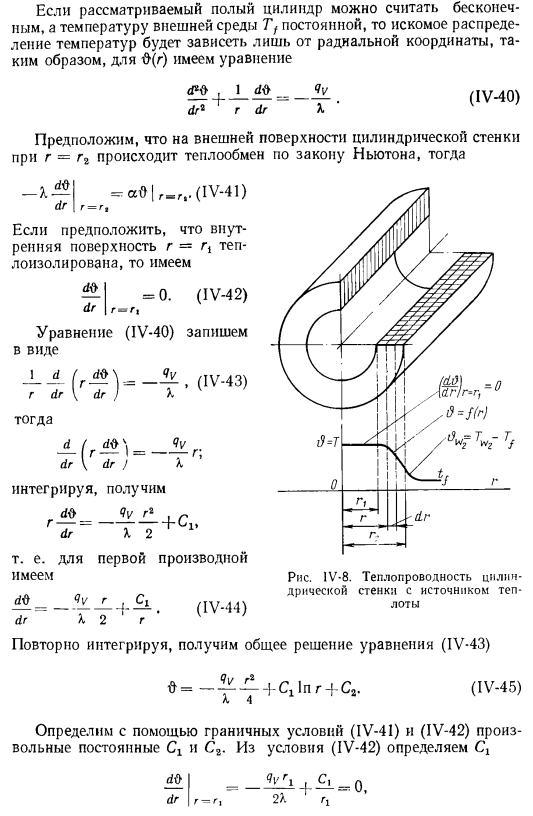
Q-присваивается единице длины стены. Преобразуйте уравнение сферической стенки (P-54) в сферическую систему координат. Используйте его для этого Следующая зависимость между Декартовыми координатами и сферическими координатами (рис. IV-5): x = r sinccosф, y = r sin 8 sinФ, z = r cos 8.Проводимость многослойной цилиндрической стенки В В сферической системе координат форма уравнения (P-54) равна dTha2?Как туда добраться, 2 at, 1 d F. dT \ₜdtL3r3g dr’g2sinea\ ae /1_g2sin26dF2] (IV-2I) рассмотрим стационарный процесс Теплопроводность внутренней поверхности (r = rx) и наружной поверхности (r =r₂) сферической стенки (оболочки) (рис. IV-6) соответственно.

Т₂. Семь Т₂ является постоянным. То есть она не зависит от направления, которое определяется углом 8 и cp. Поэтому требуемое температурное поле сферической стенки не зависит от этих переменных、 Функция радиальной переменной r. вид дифференциального уравнения (1V-2I) в этом случае равен IV-5.Корреляция декартовых и сферических координат IV-6. Для решения задачи теплопроводности граничного значения сферической конформации (IV-22, IV-23) необходимо определить распределение температуры по всей толщине сферической стенки. Переписывание Формулы (IV-22） (Ив-24) \ m2dr доктор! сначала в результате первого интеграла получается dr r* второй .

Интеграл дает Г ® =Г (IV-25).Общее использование граничных условий (IV-23) Решите уравнение (1V-25) для определения любых констант Ci и C2:r — — — rx m \ — — ^ + c2, T \ A = — — — ^ + C2. для r = r2 G # Если вы решите эти уравнения относительно C и C₂, вы получите 1 _ _ _ _ _ 1_ Заменяет \ G «-G1 G1 gg и G₂-G1 Cx и C₂ общим решением (IV-25).Упрощенный, наконец m = r = +(T₁-t₁) r \ yr от Gg-gx (IV-26) (IV-26), температура T (g） Она изменяется по толщине сферической стенки вдоль гиперболы. Определите тепловой поток из раствора (IV-26) — CL-L) ’ 1 ’» количество тепла, передаваемого через сферу 1 yy-yy.

В единицу времени, 2 =₉Г=₉.4лг2 = 4ях (л-Г₂) -!он равен а^ -. (IV-27) / ■ » — ’ 1 не зависит от r по тем же причинам, что и для цилиндрических стенок.§ 2.Теплопроводность тела с Внутренние источники тепла процессы теплопроводности в твердых телах обусловлены внешними условиями, то есть распределением температуры и теплового потока Подвод (отвод) тепла от поверхности тела и образующейся в результате внешней среды.

Математически это выражалось в выделении определенных граничных условий на поверхности тела. Рассмотрим процесс теплопередачи, когда помимо такого внешнего источника тепла существует еще и внутренний источник (сток), который распределяется определенным образом. Объем тела. Вы можете привести много примеров таких processes. It ограничивается упоминанием о том, что тепло образуется, когда электрический ток протекает через проводник.

Тепло Количество тепловыделяющих элементов выделяется и в замедлителях реактора. Когда в рассматриваемом объеме тела происходит определенная химическая реакция, он высвобождается(поглощается） В таком вопросе теплопроводности желательным обычно является распределение температуры внутри тела субъекта, а мощность внутреннего источника тепла (стока) принимается во внимание Это было дано. Мощность источника (стока) — это количество тепла, которое выделяется (поглощается) единицей объема тела за единицу времени.

Эта сумма показана в qᵥ、 Килоджоули / кубический метр / сек (kA s /l13-sec).В зависимости от характера процессов, происходящих в рассматриваемом теле, источник тепла (Сток) может выбираться по-разному. Или концентрируйтесь на определенной части или точке объема тела в течение определенного времени, или равномерно распределяйтесь по всему объему, в зависимости от температуры. Уравнения Теплопроводность при наличии внутреннего источника тепла описывается в виде cp% — = Ky’t +qᵥ. (IV-28) изменение теплоты на единицу объема за 01 единицу времени、 .

Здесь имеет место не только процесс теплопроводности, который является первым членом в правой части формулы (IV-28), но и выделение (поглощение) тепла в единице объема qv, которое мы рассмотрим ниже. Рассматривается задача о постоянном во времени и равномерно распределенном по всему источнику тепла. Теплопроводность бесконечной стенки с внутренним источником тепла плоскость YY и неограниченная стенка (рисунок IV-7) очищаются с обеих сторон при постоянной температуре жидкости Tf. Коэффициент теплопередачи .

A и выход равномерно распределены Объем qᵥ стенки источника тепла равен given. It необходимо найти распределение температуры по всей толщине стенки. Состояние поверхности стенки x = — I n x = I является постоянным, то есть, В зависимости от координат y и z температура будет функцией только от x, а уравнение (IV-28) будет иметь вид xs_ ⁼vv IV IV’2⁾.Однако, — 1 — = а(Тх ₌ / — г.) (IV-30) dx x = 1 * последний и В других случаях источник тепла может зависеть не только от координат, но и от температуры. Для аналогичных условий симметрия на поверхности x—I .

Температурное поле для плоскости x = 0 может быть заменено условием dx x-o (IV-31).От температуры очищающего раствора вводят Счетную температуру (IV-32)и затем кромку Задача (IV-29 напишите qydx2X dx x> = Q. интегрируйте уравнение (IV-33).d / \ _ _ _ _ _ Chu ’dx \ dx j X и IV-31) re — (IV-33) (IV) B 7 1 Tf X g *’ / 1 1 x рисунок IV-7.Теплопроводность плоской стенки с источником тепла после первого уплотнения приобретает вид (IV-35), а после второго уплотнения общий раствор (IV-33) получается в виде x 4-Cj. х 4-Cₜ. Граничное условие (IV-36) (IV-34) используется для определения констант /

Cx и C₂. Из (IV-35) и 2-го граничного условия (IV-34), C,= 0. dx (IV-37) в начале условия, где x = I (IV-34), получаем 2A. то есть, подставляя значение константы произведения С₂ в (IV-37), получаем решение вида (IV-38). Решение квадратично зависит от x (параболически).С другой стороны, если не было внутреннего источника, зависимость была линейной[ссылка(Iv-8)].Представьте себе решение(IV-38) Обобщенная координата. Если вы выбираете как раздел/2Liv, то все термины (IV-38), количество с размером температуры, и половина своей толщины / характерного размера стены.

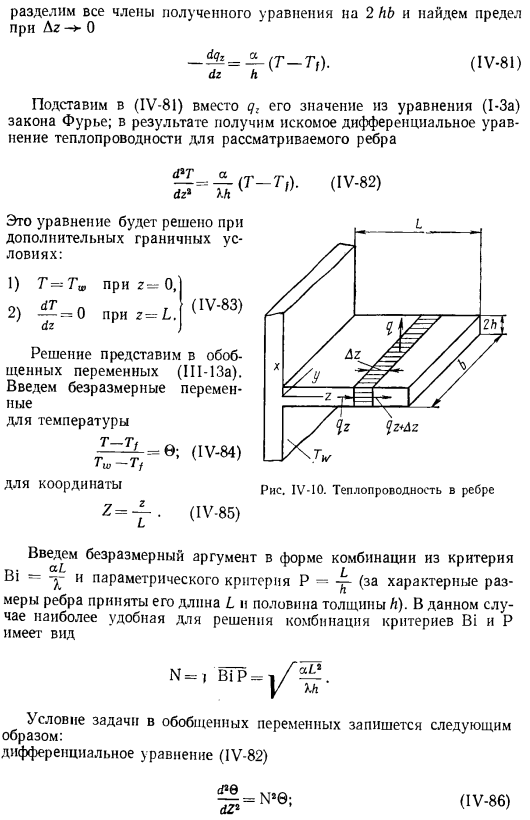
• Левая сторона (IV-39) (IV-39) является безразмерной температурой поиска. А правая сторона содержит независимые переменные в виде безразмерных координат-y и комплексных параметров Виде био-стандартом. Следовательно, (IV-39)-это (P1-13a) * q.. l2(характеристическая температура Oo = — ^ y — |является специфической функцией вида, которая получается на основе анализа） Решите уравнение (IV-33) с граничным условием (IV-34).Теплопроводность цилиндрической стенки с источником тепла делают цилиндрическую стенку (рис. IV-8) однородной.

Распределенный по всей его толщине источник тепла охлаждается снаружи жидкостью с температурой Tf \коэффициентом теплопередачи a и прочностью источника тепла qᵥ.It требуется Найти распределение температуры= = T-Tf по толщине стенки. •В этом случае вводить параметрические критерии не требуется. Если полый цилиндр в вопросе можно рассматривать Для d (g) используется уравнение dr2g, поскольку если температура окружающей среды.

Есть рисунок 1В-8.Теплопроводность цилиндрической стенки с источником тепла chu g, Cx dr X 2. Людмила Фирмаль

Tf постоянна, то желаемое распределение температуры зависит только от радиальных координат. на внешней поверхности цилиндрической стенки dr X (IV-40) r = r, предполагая, что теплообмен происходит по закону Ньютона,=: ab |(IV-41)dr r =rₜ (Ив-42) рублей. df> dr тогда dr \ dr J X если записать формулу (IV-40) в виде интеграла, то получится 1 2. ′ g (IV-44) итерационно интегрируют и получают общее решение уравнения (IV-43) 0 =—+Cilⁿr+ C»- Используйте (IV-45) A 4 граничных условия (IV-41) и (IV-42) для определения любых констант Cx и C₂.

Из условия (IV-42), M, C, ₀dr r ^rₜ2X q», то есть из условия (IV-41) определим С₂ отсюда (IV-45) и подставив значение и С₂ получим конкретное решение формулы(IV-40). Представьте себе решение (IV-46) с цилиндрической стенкой (IV-46) с обобщенными координатами(1V-46).Разделите все члены (IV-46) и выберите внешний (охлаждающий) радиус в качестве характерного размера С поверхности r2 цилиндрической стенки получаем O 4X. левая сторона (IV-47) является безразмерной искомой температурой, как и в(1V-39), а независимая переменная переходит в правую сторону. Джи! составной параметр в виде ссылки Biot, в виде g₂.

Как и в случае (IV-39), Формула (IV-47)является специфической функцией вида(1P-13a).Для цилиндрических стержень (r,= 0)обобщенная зависимость (IV-47) принимает вид (IV-48)§ 3. Теплопроводность тела с 2-мерным температурным полем 2-мерное температурное поле T-f (x, y) Получение аналитических решений, удовлетворяющих дифференциальным уравнениям и граничным условиям, рекомендуется для объектов простой формы. Для тела сложной формы решением является.

Громоздкие, в некоторых случаях недоступные. Тогда для фактического расчета аналитическое решение либо упрощается одним из численных методов аппроксимации, либо ставится задача Решайте численно в электронных вычислительных машинах и тому подобное. Мы найдем аналитическое решение дифференциального уравнения для некоторых граничных условий, которые будут представлены ниже.

Для двумерного Формат температурного поля уравнения T = T (x, y) (P-54) имеет вид^ 4-^ = 0. в качестве решения dhadu1 (IV-49)мы применяем метод разделения переменных. Найти решение уравнения в виде Произведение 2 функций, то есть T = f(x, y)= X (x)Y (y), (IV-50), где X (x) — функция только переменной x. Y (y) является функцией только переменной y. Формула т из(IV-50) (1V-49), после деления на X и Y,\ _dtY__________ 1 вы получите d * XY dy * XX1 (IV-51).Поскольку левая сторона (IV-51) не зависит от x и равна значению (правая сторона), это если вы не зависите от y, общие (оба) значения не зависят от x или y. таким образом, общее значение (для обеих частей) уменьшается до постоянного значения. Это полезно для принятия формы k2.

Как и в (IV-56), напишите общее решение (IV-53) X = Cxeⁱkx+C₂e〜ⁱkx, (IV-59).Здесь (\и С₂-произвольные константы. Однако формулы e1x и е-1 actually на самом деле фактические значения х, кроме Х = 0.Используя Эйлера официальный e±ТТХ₌потому что£Х±З Син х (ИЖ-60) (ИЖ-59)* х — сов / экс-ЖБ грех КХ. (ИЖ-61） Можно написать общее решение Формулы (IV-59) на основе (IV-60) в виде T = x XU =(AcosЛх4-Bsin KX) (SEC>〜J-de-K>) (IV-62).

Применяйте его для решения конкретных задач. Теплопроводность плоских стенок с 2-мерным температурным полем рассмотрим конкретную задачу теплопроводности плоских стенок (рис. IV-9).Пусть T-форма температурного поля на стене = /(х,//), температуры в направлении оси Z во всех точках (вдоль стены толщина) X = СЈ е ’ * — r4C₂e -и KX = Ки(coskx + я грешу опций)-| −4- СГ (потому что / с GX-мне грех КХ)=(СЈ-Ф-C₂) потому что с KX + я (Cₜ-C₂） грех КХ — = а потому что КХ ^ — ПБ грех КХ -, (а = с ^ СГ, 5 = ^ −0.).

Тот же смысл. Избыточная температура(гл. Уравнение Лапласа (P-56) для этой задачи в 111,§ 2) имеет вид dx2du2. Граничное условие типа 1 O = T-Ta = 0 задается для x = 0 и x = L. где 0-искомая избыточная температура стенки. Ta-поддерживается температура боковой стенки Постоянный. (IV-63) (IV-64) 0 — > 0 как y — > — oo. (IV-66) (рисунок 1V-9) рисунок IV-9. Теплопроводность в 2D температурном поле, Т= / (*•У) где 7 \ — температура на нижнем конце (см. Рисунок). 1В-9) стены поддерживаются постоянными.

Решением уравнения (IV-63) будет уравнение (1V-62). в последнем случае абсолютная переменная температуры T заменяется избыточной переменной F. Используя граничные условия (IV-64 и IV-66), определите постоянные коэффициенты A, B, C, D. Из первого условия(1V-64) выполните x-0 и A-0. x = 0 должен быть равен нулю, но cosx |z₌ ₀ = coso = 1, то есть если он не равен пуле, то коэффициент a должен быть равен нулю. Поскольку нас интересуют нетривиальные решения, а именно, они не равны нулю Аналогично коэффициент B равен нулю, поэтому если x = L, то требуется sinkL 0.Значение нетривиального решения, удовлетворяющего границе уравнения (IV-63) .

Условие (IV-64) называется собственным значением, а нетривиальное решение этой задачи называется собственной функцией, соответствующей заданному eigenvalue. So кл- ПЛ, вот н= 0、1、2、3、…в результате k>/ / L, k₂-2n / L,…kₙ= !! Си.,…Из условия (IV-66) следует, что коэффициент C = 0 (y — * oo, если e * y неограничен） Рост.) При A = 0, C-0 решение(1V-62) не может принимать вид^-BDe sin ^-^-x ^ =£e sin ^ — ^ ^ x ^ (IV-67) решение (IV-67) удовлетворяет дифференциальному уравнению (1V-63). любое натуральное значение n. из полученного решения (IV-67) видно, что для 7 -Ta 0 условие (IV-65) не выполняется для выбора E-En. 0 после этого .

Единственным решением проблемы является тривиальное решение 0 = 0.С другой стороны, сумма любых 2 (и, следовательно, любого конечного числа) решений линейных однородных производных Уравнение также является решением. Если мы суммируем число решений типа (IV-67) до бесконечности, то увидим, что мы можем выбрать E = En так, чтобы условие (IV-65) было выполнено(или、 Условие (IV-66)] и бесконечная сумма d = 2£e_T «sin (- ^x’) (IV-68) сходятся, а краевые задачи (IV-63), (IV-64), (IV-65) и (IV-66) сходятся.

Как найти Ep Используйте граничное условие (IV-68) (IV-65). если y = 0, то форма выражения (IV-68) равна (IV-69). чтобы понять формулу (IV-69), вспомним следующее положение из математики. Функция является F (x)с периодом 2n дифференцируема или, по крайней мере, кусочно дифференцируема и может быть расширена рядом Фурье следующих форм: где a0, an и bn Величина, которая называется коэффициентом ряда Фурье и определяется по формуле: lnp-j /(x) cosnxJx (l = 1,2 t 3,…(IV-71) — — — l l°0 = ’ T (IV-713) — — — l l 6n = — J — (F (x) sin nxdx(n = l, 2, 3. ). л.(ИЖ-72) с / — — — Л. Если F (х) нечетная функция (χχ) потому что NX-это странно. Помнишь? В случае нечетной функции выполняется равенство f (- x)= — f (x).

Тогда об этом л§f (x) dx = 0-и, следовательно, в случае (IV-71) an = jf (x) cos nx dx = 0(n = 1, 2, 3,…). — Я имею в виду… Вид ряда Фурье нечетных функций (IV-70) имеет вид f(x)= S b sin px. Чтобы определить bn из (IV-73) n = I (IV-72), для четной функции используйте равенство f (- X) 0), то, изменив переменную, можно переписать Формулы (IV-73) и (IV-75) в виде ZW = BS&». грех (- ПХ） (IV-76) и L sino теперь возвращаются к Формуле (IV-69).

Положим Dx)=в этом случае Формулы (IV-69)и(IV-76) идентичны. Таким образом, выражение (IV-69) представляет собой ряд Фурье следующих констант: Интервал 10, ZJ(Z7 > 0).Константа En равна Ln и по формуле (IV-77) y-x)/ x, где n = 1,2,3……….(IV-77) 0 n = 1, 3, 5, cos pl—1 = n = 2, 4, 6, cos pl-4-1 и En = 0.Конкретные решения (IV-68) могут быть записаны в окончательном виде (IV-78).Здесь мы используем следующие результаты: если функция Dx) с периодом разлагается равномерно В случае сходящегося ряда последний должен быть ближе к Фурье. (Серия (IV-78) четко сходится равномерно.

Отметим, что согласно (IV-78), температура стенки в любой точке не зависит. Теплопроводность в случае учета отсутствия теплового потока на стене. Из полученного решения также ясно, что если = 0, то решение 0 = 0.§ 4. При передаче тепла от жидкости (а.) до падения теплопроводности в ребрах определенных пересечений через сплошную стенку к газу (А₂), общее тепловое сопротивление!K определяется. 4 -= по формуле (1-12)-+ 4-± ИЖ — ⁷⁹ > к-Аль — Xa₂ последний срок 1 /a₂ вносит наибольший вклад в общее тепловое сопротивление, 1, а в некоторых случаях и 2-х значное число больше, чем первых 2-х значное число членов 1 / aP обычно, a₂ не может быть увеличен.

Кроме того, для усиления теплопередачи поверхность стенки со стороны газа увеличена ребрами. Рассмотрим теплопроводность некоторой кромки Раздел 1112).Упростите фактический процесс и предположите следующее: 1)температура ребра T изменяется только вдоль оси Z. 2) тепло передается только в окружающую среду Верхняя (Lb) и нижняя (Lb) поверхности ребра. 3) коэффициент передачи тепла от края нервюры к окружающей среде a постоянн значение, и поток тепла Формула = a (T-T.), (IV-80), где Tf-температура окружающей среды.

Выведем дифференциальное уравнение теплопроводности для ribs. To для этого создадим уравнение теплового равновесия выделенного объема qz2hb-qz + bz2hb-a (2b & z) (T-Tj)= ребро в виде 0 (рисунок IV-10).Разделите все члены полученного уравнения на 2 hb и найдите ограничение Az O (IV-81) dz h. подставьте (IV-81) вместо q. Значение из уравнения закона Фурье (1-Za). в результате получаем искомое дифференциальное уравнение теплопроводности для рассматриваемого ребра dza.

Дополнительные граничные условия: 1) t = Tda (IV-83) решение z = O, z-L обозначается обобщенной переменной (III-13a).Введение температурных безразмерных параметров (IV-84） ’W-координата 2 tf= -^ -. (IV-85) (IV-82) эталонный Bi = — y и параметрический эталонный P = — (для характерных размеров ребер、 Его длина L и половина толщины L). в этом случае наиболее удобное для решения сочетание критериев Bi и P принимает вид: условие задачи обобщенной переменной описывается следующим образом:.

Дифференциальные уравнения (IV-82) (IV-86) дополнительные граничные условия (IV-87) и решение системы br = o = 1 (IV-88) (IV-86, IV-87, IV-88) получены с помощью гиперболической функции в виде Или позвольте мне ввести характеристики эффективности реберной кости 8-NZ-(THN) sh NZ (IV-89) chN (l-Z) ch N (IV-90).Используйте отношение тепло которое на самом деле в качестве его меры Тепло, рассеиваемое поверхностью ребра, рассеивается, если температура всей поверхности ребра равна Tw. As в рассматриваемом случае и эффективность ребер Формула fOdZ-т — — — — — — — — — — — 5-L «1-г > I» (IV-91) о (IV-92) может быть определена.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Теплопроводность плоской, цилиндрической и сферической стенок при стационарном режиме

Рисунок 7.3 – К выводу уравнения теплопроводности плоской стенки

Теплопроводность плоской стенки. Тепловой поток перемещается через плоскую стенку толщиной δ (рис. 7.3) из однородного материала, имеющего коэффициент теплопроводности .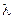

На наружной поверхности стенки поддерживаются постоянные температуры и ( > ). Температура изменяется только в направлении оси х, перпендикулярной плоскости стенки, т.е. температурное поле одномерно, а изотермические поверхности плоские и располагаются перпендикулярно оси х.

В соответствии с дифференциальным уравнением теплопроводности (7.23) .

В результате интегрирования этого выражения получим:

.

Таким образом, температура по толщине плоской стенки при установившемся тепловом режиме изменяется линейно, а градиент температуры сохраняет постоянное значение.

Константы интегрирования и определяют из граничных условий:

При , следовательно ;

При ,

.

С учетом найденных констант:

. (7.25)

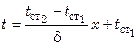
Дифференцируя последнее уравнение, имеем: .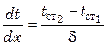

Подставив найденные значения температурного градиента в уравнение, выражающее основной закон теплопроводности (7.12), получим уравнение теплопроводности для плоской стенки при стационарном режиме:

, (7.26)

.

Рисунок 7.4 – К выводу уравнения теплопроводности плоской многослойной стенки

Отношение (l/d) носит название тепловой проводимости стенки, а (d/l) – термического сопротивления стенки.

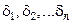
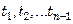
Если стенка многослойная(рис. 7.4), состоит из n слоев толщиной с коэффициентами теплопроводности соответственно, при этом температуры наружных поверхностей и , а температуры на границе слоев , то при установившемся тепловом режиме тепловой поток Q, проходящий через каждый слой, одинаков и уравнение теплопроводности для каждого из них может быть выражено уравнением (7.26):

для 1-го слоя , или ;

для 2-го слоя 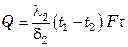, или ; (7.27)

для n-го слоя , или .

Складывая левые и правые части выражение (7.27), получим уравнение теплопроводности плоской многослойной стенки для стационарного режима:

, (7.28)

где i – порядковый номер слоя.

Таким образом, общее термическое сопротивление плоской многослойной стенки равно сумме термических сопротивлений отдельных слоев стенки при условии, что слои плотно прилегают друг к другу. Внутри каждого слоя линия изменения температуры (рис. 7.4) – прямая, но для многослойной стенки в целом она представляет собой ломаную линию.

Рисунок 7.5 – К выводу уравнения теплопроводности цилиндрической стенки

Теплопроводность цилиндрической стенки. В однородной цилиндрической стенке длиной L (рис. 7.5) температура в случае одномерного стационарного поля изменяется только в радиальном направлении, поэтому для поверхности произвольного радиуса r уравнение Фурье можно представить в виде

. (7.29)

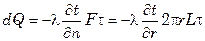
Для кольцевого слоя с радиусом r и толщиной dr, выделенного внутри стенки (рис. 7.5), при внутреннем и наружном радиусах соответственно r₁ и r₂ и температурах на внутренней и наружной поверхностях стенки и , согласно уравнению (7.29) имеем:

.

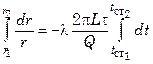
В результате интегрирования последнего выражения получим:

(7.30)

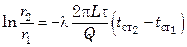
либо .

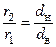
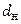
Если учесть, что ( и – наружный и внутренний диаметры цилиндра соответственно), то:

. (7.31)

Уравнения (7.30) и (7.31) являются уравнениями теплопроводности цилиндрической стенки при установившемся процессе теплообмена. Они показывают, что по толщине цилиндрической стенки (в отличие от плоской) температура изменяется криволинейно – по логарифмическому закону. При этом влияние кривизны стенки учитывается коэффициентом кривизныφ, значение которого определяется отношением диаметров . При

Рисунок 7.6 – Теплопроводность многослойной цилиндрической стенки	Рисунок 7.7 – К выводу уравнения теплопроводности сферической стенки

В соответствии с законом Фурье количество тепла, проходящее через шаровой слой толщиной dr и радиусом r

. (7.34)

В результате разделения переменных и интегрирования этого выражения в соответствующих пределах, получим:

,

, (7.35)

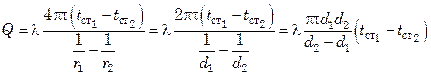
где и – диаметры внутренней и внешней поверхности соответственно.

Уравнения (7.35) являются расчетными формулами теплопроводности сферической стенки. Как следует из них, при 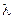= сonst температура в сферической стенке меняется по закону гиперболы.

По аналогии с плоской и цилиндрической стенками для многослойной сферической стенки

. (7.36)

Тепловое излучение

В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда наблюдается и тепловое излучение, причем, чем выше температура тела, отдающего тепло, тем большее количество тепла передается в виде лучистой энергии.

Тепловое излучение представляет собой процесс распространения внутренней энергии излучающего тела путем электромагнитных волн. При поглощении электромагнитных волн какими-либо другими телами они вновь превращаются в энергию теплового движения молекул. Источниками электромагнитных волн являются заряженные материальные частицы, т.е. электроны и ионы, входящие в состав вещества. По своей природе тепловое излучение аналогично излучению света, оба они представляют собой один вид энергии – лучистой – и подчиняются одним и тем же законам отражения, преломления и поглощения. Соответственно этому тепловое излучение характеризуется длиной волны. Однако в отличие от видимых световых лучей, имеющих длину волн 0,4÷0,8 мкм, длина волн теплового излучения лежит в основном в невидимой (инфракрасной) части спектра и составляет 0,8÷40 мкм.

Все тела излучают и поглощают лучистую энергию непрерывно. Интенсивность излучения зависит от природы тела, его температуры, длины волны, состояния поверхности, а для газов – еще от толщины слоя и давления. Твердые и жидкие тела имеют значительные поглощательную и излучательную способности. Вследствие этого в процессах лучистого теплообмена участвуют лишь тонкие поверхностные слои. Поэтому в этих случаях тепловое излучение приближенно можно рассматривать как поверхностное явление. Газы и пары характеризуются объемным характером излучения, в котором участвуют все частицы объема вещества. Излучение всех тел зависит от температуры. С увеличением температуры тела его энергия излучения увеличивается, так как увеличивается внутренняя энергия тела. При этом изменяется не только значение этой энергии, но и спектральный состав. При увеличении температуры повышается интенсивность коротковолнового излучения и уменьшается интенсивность длинноволнового излучения. В процессах излучения зависимость от температуры значительно большая, чем в процессах теплопроводности и конвекции. Вследствие этого при высоких температурах основным видом переноса тепла может быть тепловое излучение.

Лучистая энергия распространяется в однородной и изотропной среде прямолинейно. В отличие от теплопроводности и конвекции, лучистый теплообмен происходит не только между соприкасающимися, но и между удаленными друг от друга телами. Поток лучей, испускаемый нагретым телом, попадая на поверхность другого лучеиспускающего тела, частично поглощается, частично отражается (при этом угол падения равен углу отражения) и частично проходит сквозь тело без изменений, т.е.

; (7.37)

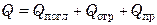
то есть ,

где – общая энергия падающих на тело лучей; – энергия, поглощенная телом; – энергия, отраженная от поверхности тела; – энергия лучей, проходящих сквозь тело без изменений.

Таким образом, отношения , и характеризуют поглощательную, отражательную и пропускательную способности тела. Если тело полностью поглощает падающую на него лучистую энергию, т.е. , а и равны нулю, то оно носит название абсолютно черного. При полном отражении телом лучистой энергии, , а , такие тела называют абсолютно белыми. Наконец, если тело пропускает все падающие на него лучи, не поглощая их и не отражая, , а , его называют абсолютно прозрачным или диатермичным.

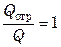
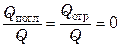
В природе не существует абсолютно черных, абсолютно белых и абсолютно прозрачных тел. Все тела в той или иной степени поглощают, отражают и пропускают сквозь себя падающие на них лучи, т.е. являются серыми. Однако твердые тела и жидкости практически непрозрачны для тепловых лучей, а большинство газов, наоборот, диатермичны.

Основные законы излучения

Закон Стефана-Больцмана. Количество тепла, излучаемого единицей поверхности тела в единицу времени, называют лучеиспускательной способностью тела Е, Вт/м 2 :

. (7.38)

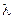
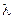
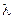
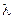
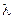
Как указывалось ранее, энергия излучения зависит от длины волн и температуры Т. Характеристикой энергии излучения по длинам волн служит интенсивность излучения I – лучеиспускательная способность тела в интервале длин волн от до + d , отнесенная к этому интервалу d , т.е.

. (7.39)

Лучеиспускательная способность тела E является интегральной характеристикой, которая учитывает энергию излучения волн всех длин от λ = 0 до λ = ∞.

. (7.40)

На основании электромагнитной теории света Планком аналитически была определена функциональная зависимость интенсивности излучения I₀ от температуры и длины волн для абсолютно черного тела. Согласно этой зависимости

, (7.41)

где c₁ – константа, равная 3,74∙10 –16 Вт/м 2 ; с₂ – константа, равная 1,44∙10 –2 (м∙К).

Интегрирование выражения (7.40) с учетом (7.41) дает зависимость для определения лучеиспускательной способности абсолютно черного тела Е₀:

, (7.42)

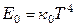
где к₀ – константа излучения абсолютно черного тела,
к₀ = 5,67∙10 –8 Вт/(м 2 ∙К 4 ).

Зависимость (7.42) носит название закона Стефана–Больцмана, так как была найдена экспериментально Стефаном и подтверждена Больцманом до того, как Планк вывел соотношение (7.41).

Таким образом, согласно закону Стефана–Больцмана, лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры.

При проведении технических расчетов выражение (7.42) удобнее использовать в виде

, (7.43)

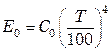
где С₀ – коэффициент излучения абсолютно черного тела, равный С₀ = k₀∙10 8 = 5,67 Вт/(м 2 ∙К 4 ).

Исследования показали, что закон Стефана-Больцмана применим не только к абсолютно черным телам, но и к серым. В этом случае его записывают в виде

(7.44)

(C по аналогии с абсолютно черным телом называют коэффициентом излучения серых тел).

Отношение коэффициентов излучения данного тела и абсолютно черного С/С₀ = e носит название относительной излучательной способности или степени черноты данного тела. С учетом этого понятия закон Стефана-Больцмана принимает вид

. (7.45)

Рисунок 7.8 – К выводу закона Кирхгофа

Закон Кирхгофа устанавливает соотношение между лучеиспускательной и поглощательной способностями тел. Это соотношение может быть получено из рассмотрения процесса обмена лучистой энергией между абсолютно черным и серым телами (рис. 7.8).

Поверхности рассматриваемых тел параллельны и расположены на расстоянии, при котором излучение каждого из тел попадает на другое. Абсолютно черное тело имеет температуру T₀, лучеиспускательную способность E₀ и поглощательную A₀ = 1, серое тело имеет соответственно Т, Е и А, при этом Т > T₀. Излучение Е попадает на абсолютно черное тело и целиком им поглощается. Излучение E₀ попадает на серое тело. При этом часть этого излучения, равная E₀А, поглощается, а другая часть, равная E₀(1 – А), отражается на абсолютно черное тело и поглощается им. В результате этого обмена абсолютно черное тело получает суммарное количество энергии:

. (7.46)

При выравнивании температур обоих тел наступает тепловое равновесие, при котором Q = 0, т.е. . Следовательно,

. (7.47)

Последнее соотношение является математическим выражением закона Кирхгофа, согласно которому отношение лучеиспускательной способности тел к их поглощательной способности для всех тел одинаково, равно лучеиспускательной способности абсолютно черного тела при той же температуре и зависит только от температуры.

В результате подстановки значений E и E₀ из равенств (7.44) и (7.45) в соотношение (7.47) получаем

. (7.48)

Рисунок 7.9 – К формулировке закона Ламберта

Так как , то , т.е. способность тела к поглощению излучения численно равна степени его черноты. Учитывая, что e и A изменяются в пределах от 0 до 1, из равенства (7.47) следует, что лучеиспускательная способность реального тела всегда меньше лучеиспускательной способности абсолютно черного тела при той же температуре.

Закон Ламбертаопределяет изменение интенсивности излучения по различным направлениям. Согласно этому закону излучение энергии элементом поверхности в направлении элемента (рис. 7.9) пропорционально излучению dQ (по направлению нормали к ), телесному углу dψ (под которым виден элемент из элемента ) и косинусу угла φ, образованного прямой, соединяющей элементы и , и нормалью к элементу .

При этом лучеиспускательная способность в направлении нормали в p раз меньше полной лучеиспускательной способности тела.

Таким образом, количество энергии, излучаемой элементом в направлении элемента :

. (7.49)

Электронная библиотека

Дифференциальное уравнение теплопроводности при стационарном режиме без внутренних источников теплоты имеет вид:

Для решения конкретной задачи к этому уравнению надо присовокупить соответствующие граничные условия. Рассмотрим несколько простейших случаев определения стационарного поля температур в телах различной формы.

Рассмотрим неограниченную тонкую стенку толщиной (рис. 10.5).

Рис. 10.5. Схема для определения стационарного поля температур в телах с плоской стенкой

Пусть на поверхностях стенки поддерживаются соответственно температуры и . Если и не зависят от z и y, то очевидно, искомое температурное поле тоже не будет зависеть от этих координат и тогда:

При отыскании распределения поля температур используем граничные условия:

при

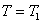
Представим выражение (10.2) в виде:

После первого интегрирования имеем:

После второго интегрирования имеем:

Постоянные и определим из граничных условий. Из первого граничного условия имеем:

из второго граничного условия определим константу :

Таким образом, решением уравнения (10.2) будет выражение:

т.е. функция T(x) линейно зависит от x.

Найдем плотность теплового потока. Согласно закону Фурье:

или в данном случае:

Определим количество теплоты потока через стенку в единицу времени:

где F – площадь стенки.

Теперь определим плотность теплового потока через трехслойную стенку (рис. 10.6).

Рис. 10.6. Определение плотности теплового потока через трехслойную стенку

Для каждого слоя можно записать следующие выражения:

для первого слоя

для второго слоя

для третьего слоя

Из уравнений (10.3) – (10.5) можно найти термическое сопротивление трехслойной стенки. Для этого сначала определим местные температурные напоры на каждой стенке:

Почленно сложив эти уравнения, получим:

На основании последнего выражения для многослойной стенки получим:

где n – количество слоев.

С вводом обозначения

где – эквивалентная теплопроводность, выражение (10.6) можно представить в виде:

Запишем дифференциальное уравнение теплопроводности в цилиндрической системе координат.

Для этого используем известные соотношения, связывающие декартовы и цилиндрические координаты (рис. 10.7):

Рассмотрим одномерный процесс теплопроводности в бесконечной цилиндрической стенке (рис. 10.8). Предположим, что на внутренней и внешней полостях стенки, температура не зависит от угла . Тогда получим:

Зададим граничные условия задачи:

при ;

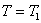
Рис. 10.7. Переход от декартовых к цилиндрическим координатам

Рис. 10.8. Одномерный процесс теплопроводности в бесконечной цилиндрической стенке

Приведем уравнение (10.8) к виду:

После первого интегрирования получим:

После второго интегрирования имеем:

Постоянные интегрирования определим из граничных условий:

Вычитая из уравнения(10.11) выражение (10.10) получим:

Постоянную найдем из уравнения (10.10):

Подставляя выражения для и в уравнение (10.9), найдем:

Из последнего выражения видно, что искомое распределение температуры по толщине цилиндрической стенки логарифмически зависит от координаты r.

Плотность теплового потока определим из закона Фурье:

Количество теплоты, проходящее сквозь цилиндрическую стенку, через единицу длины:

Используя последнюю формулу можно определить количество теплоты, проходящее сквозь многослойную цилиндрическую стенку: