Дифференциальное уравнение упругой линии балки и его интегрирование
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

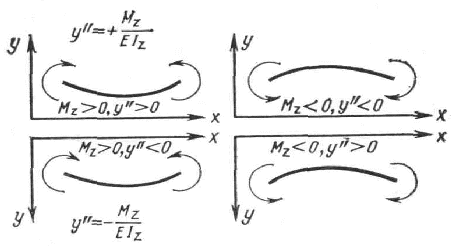
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений

а после второго интегрирования – прогибы балки

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Дифференциальное уравнение упругой линии
Упругую линию балки можно рассматривать как график некоторой функции, определяемой характером нагружения балки, ее размерами и материалом. Сама функция представляет собой текущую ординату упругой линии, а ее аргументом является абсцисса центра тяжести произвольного поперечного сечения балки, т. е.
Для определения этой функции воспользуемся зависимостью между кривизной К оси балки (кривизной нейтрального слоя) и изгибающим моментом Мх и жесткостью сечения балки при изгибе EJх
Из курса математики известно следующее выражение кривизны некоторой кривой, которое для принятой на рис. 7.1 системы координат запишется в виде
К= 
где 

Подставляя это значение К в выражение (7.2), получим точное дифференциальное уравнение изогнутой оси балки (упругой линии)

Первая производная 



Данное выражение называется приближенным дифференциальным уравнением упругой линии.Для балокпостоянного сечения его обычно записывают в виде
EJх 
Правая часть зависимости (7.6) представляет собой уравнение изгибающих моментовт.е. аналитическое выражение закона изменения изгибающего момента по длине балки.
Для вычисления углов поворота θ ≈ 
Проинтегрировав уравнение один раз, получим уравнение углов поворота
EJх 

где С – постоянная интегрирования.
Интегрируя второй раз, получим уравнение прогибов
EJх v= 

где D – вторая постоянная интегрирования.


Определив постоянные интегрирования, можно из уравнений (7.7) и (7.8) определить угол поворота и прогиб любого сечения.
Пример.Двухопорная балка длиной l (рис. 7.2) нагружена силой F, расположенной на расстоянии а от левой опоры. Требуется составить уравнение упругой линии и найти перемещение в сечении на расстоянии z.
Решение.Начало координат располагаем на левой опоре. Опорные реакции RA и RB соответственно составят
RA= F 

Изгибающие моменты на первом и втором участках балки имеют выражения
M1= F 

Дифференциальное уравнение упругой лини балки имеет вид (7.4)


После однократного интегрирования находим угол поворота сечения балки на опоре А
θA= 

Угол поворота на правой опоре B:

После двукратного интегрирования прогиб в сечении на расстоянии z от левой опоры:
v= 
v= 
Так как поперечная сила Q имеет разрыв первого рода в точке z=a, то функции M, q, n не могут быть выражены аналитически одним выражением.
Постоянные интегрирования, вошедшие в приведенные выше выражения, определены из граничных условий (условий закрепления балки).
Оборудование, приборы и материалы:лабораторная установка,подвеска с набором грузов, индикаторы часового типа, штангенциркуль, линейка.
Описание установки
Схема установки приведена на рис. 7.2 . Как видно из схемы левая опора А балки 1 прямоугольного поперечного сечения является шарнирнонеподвижной, а правая В – шарнирноподвижной. Материал балки – сталь, Е= 2∙10 5 МПа, размеры поперечного сечения: ширина b1 , толщина h.
Рис. 7.2. Схема лабораторной установки
С левым концом балки 1 жестко соединена планка АC длиной r. Нагрузка F на балку 1 создается подвеской 2 с набором грузов 3. Подвеска может перемещаться вдоль балки и крепиться на ней в любом сечении. Прогиб балки фиксируется индикатором 4, корпус которого крепится к подвижной стойке, что позволяет перемещать его вдоль балки и производить измерения в любом ее сечении. Величина угла поворота θ сечения балки на опоре А после приложения нагрузки F приближенно определяется через смещение ΔС точки С, фиксируемое индикатором 5, корпус которого закреплен на опоре. Так как при изгибе балки в пределах упругих деформаций угол поворота сечения мал, можно с достаточной степенью точности считать длину дуги, описываемой при деформации балки точкой С, примерно равной ее хорде ΔС. Тогда центральный угол θ этой дуги составит
Порядок проведения работы
1. Ознакомиться с лабораторной установкой, зарисовать схему нагружения испытываемой балки, записать размеры длин участков (l, а, АС=r) и поперечного сечения (h, b).
2. В сечении балки, указанном преподавателем, закрепить подвеску 2 (см. рис. 7.2).
3. Установить стойку с индикатором 4 в одном из сечений, в которых будет замеряться прогиб балки (z1= l /4; z2= l / 2; z3=a).
4. Поворотом ободков индикаторов 4 и 5 выставить их показания на ноль.
5. Установить на подвеску набор грузов 3, обеспечив заданную преподавателем нагрузку F. Записать показания соответствующих индикаторов (vэксп, ΔС) в таблицу 7.1.. Рассчитать значение θ.
6. Снять с подвески грузы, передвинуть стойку с индикатором 4 на следующее сечение балки; обнулить показания индикатора 4, затем установить снятые грузы на подвеску и записать показания индикатора в таблицу 7.1.
7. Выполнить действия в соответствии с п. 6 для всех сечений балки, где необходимо определить прогибы, и записать показания индикатора в таблицу 7.1.
8. Рассчитать осевой момент инерции сечения балки Jx=bh 3 /12.
9. Произвести теоретический расчет угла поворота сечения θ на опоре А и прогибов vтеор для тех же сечений, что и при экспериментальном определении (т.е. при z1= l/4; z2= l/2; z3=a).
10. Вычислить расхождение в процентах между расчетными и опытными значениями угла поворота и прогибов.
11. По данным теоретического расчета построить в масштабе упругую линию балки.
| z, мм | vэксп, мм | vтеор, мм | ΔС, мм | θэкпп, рад | θтеор, рад |
| z1= l/4 = | |||||
| z2= l/2 = | |||||
| z3=a = |
Вопросы для самопроверки
1. Что называется балкой?
2. Что такое прогиб, стрела прогиба?
3. Что понимается под упругой линией балки?
4. Что такое угол поворота сечения балки?
5. В каком случае изгиб балки считается прямым?
6. Что называется жесткостью балки при изгибе?
7. В какой точке расположен центр изгиба (центр инерции) однородной балки с поперечным сечением, показанным на рисунке?

8. Какая из балок имеет большую жесткость (материал одинаковый)?
9. Во сколько раз изменится прогиб балки в исследованной Вами точке, если балку развернуть вокруг своей оси на 90°?
10. Во сколько раз изменится прогиб балки в исследованной Вами точке, если все линейные размеры балки пропорционально увеличить в 2 раза, а вес груза и материал балки оставить неизменным?
11. Какие внутренние силовые факторы действуют в сечениях балки при чистом изгибе?

1. Степин П.А. Сопротивление материалов: учебник для немашиностроительных специальностей вузов / П.А.Степин. – М.: Высш. школа, 1988.– 366 с.
2. Копнов В. А. Сопротивление материалов: руководство для решения задач и выполнения лабораторных и расчетно-графических работ / В. А. Копнов. – М. : Высш. школа, 2003. – 351 с.
3. Рубашкин А. Г. Лабораторные работы по сопротивлению материалов /А.Г. Рубашкин – М. : Высш. школа, 1982. – 240 с.
4. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев ; отв. ред. Г. С.Писаренко. – 2-е изд., перераб. и доп. – Киев : Наукова думка, 1988. – 736 с.
5. Афанасьев А. М. Лабораторный практикум по сопротивлению материалов / А. М. Афанасьев, В. А. Марьин. – М. : Наука, 1975. – 284 с.
6. Кирносов В.Н. Измерение механических характеристик материалов. уч. пособие/ В.Н. Кирносов.– М.: Изд-во стандартов, 1976. – 240 с.
7. Феодосьев В. И. Сопротивление материалов / В. И. Феодосьев. – М. : Наука, 1999. – 456 с. (МГТУ им. Баумана, 2005. 591 с).
8. Электрические измерения электрических и неэлектрических величин / под ред. Е. С. Полищука. – Киев : Вища школа, 1984. – 359 с.
ПРИЛОЖЕНИЯ
Механические характеристики сталей (по ГОСТ 380–94)
СОПРОМАТ ОН-ЛАЙН
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции — теория, практика, задачи.
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Книги — разная литература по теме.
Базовый курс лекций по сопромату, теория, практика, задачи.
4. Изгиб. определение перемещений.
4.1. Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки.
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):
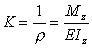
В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,
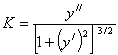
Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем
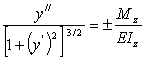
Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки
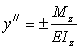
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений
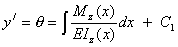
а после второго интегрирования – прогибы балки
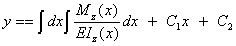
Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
http://allrefrs.ru/3-24775.html
http://www.sopromat.org/info/4/4_1.php