Дифференциальное уравнение установившегося плавно изменяющегося движения жидкости.
Дифференциальное уравнение установившегося плавно изменяющегося движения жидкости.
Дифференциальное уравнение установившегося плавно изменяющегося движения жидкости. В предыдущей главе в основном рассматривалось движение напора жидкости. Там форма и размеры живого сечения потока полностью определялись формой и размером поперечного сечения самого канала. Наличие локального сопротивления в потоке давления приводит к локальным изменениям биозащиты. 20. 307. При движении жидкости в открытом канале (включая частично заполненные и закрытые каналы) локальные изменения условий движения (такие как расширение, закупорка и разрушение дна канала) неизбежно вызывают деформацию некоторых (в некоторых случаях очень важных) участков биотрансплантата, его length. In в этом случае все точки свободной поверхности по-прежнему подвергаются воздействию внешнего давления газовой среды, поэтому деформация живой части потока неизбежно связана с изменением координат ее свободной поверхности.
В предыдущих главах рассматривалось в основном напорное движение жидкости, при котором форма и размеры живого сечения потока полностью определялись формой и размерами сечения самого русла. Наличие местных сопротивлений в напорных потоках приводит к локальным изменениям живого сечения. Людмила Фирмаль
- В этой главе описывается плавное, установившееся движение жидкости в открытом состоянии. water. In в этом случае основные параметры течения по длине изменяются очень плавно(см. 3.5).в связи с этим при выводе уравнений движения можно пренебречь составляющими локальной скорости в плоскости живой части потока и сделать распределение давления в этой плоскости соответствующим закону гидростатики pressure. It также предполагается, что работа силы сопротивления при практически равномерном движении и равномерном движении примерно одинакова. В следующей презентации мы отмечаем, что открытые каналы, встречающиеся в инженерной практике, можно разделить на 2 категории: призмы и непризмы. Призменный канал включает в себя канал, в котором основные геометрические параметры потока остаются постоянными по всей его длине. Живая площадь поперечного сечения призмы канала потока зависит от глубины канала. ©= /(Ля.) (15.1) В общем случае непризматических каналов площадь биофизического разреза является функцией 2 переменных. Людмила Фирмаль
- Для выбранного сечения мы создаем уравнение Бернулли для плоскости O-0, проходящей через точки под живым сечением 2-2. К + Ш + ^ + −2 ^ = к + а+ -& -+ -?1А+*’) ’ + . (15.3) В АК Н! ар. игнорировать [(yn) 2 из-за малости, n2 ^ / / C2 /? ® 3Г = Я (15.8) 41a2с2ii\ла3 Если вычесть преобразование правой части выражения (15.7) или (15.8) в знаменателе, то получится ВОш2! § 2




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Дифференциальные уравнения установившегося неравномерного плавно изменяющегося движения жидкости
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ УСТАНОВИВШЕГОСЯ НЕРАВНОМЕРНОГО ПЛАВНО ИЗМЕНЯЮЩЕГОСЯ ДВИЖЕНИЯ ЖИДКОСТИ
2.1. УРАВНЕНИЯ НЕРАВНОМЕРНОГО ПЛАВНОИЗМЕНЯЮЩЕГОСЯ ДВИЖЕНИЯ ЖИДКОСТИ
2.1.1. Уравнения неравномерного плавноизменяющегося движения жидкости в непризмагических руслах
Уравнение неравномерного плавноизменяющегося движения в непризматическом русле с прямым уклоном дна записывается в следующем виде:

Аналогичные выражения с учетом знака уклона могут быть получены для призматических русл с горизонтальным и обратным уклонами дна.
Рекомендуемые материалы
2.1.2. Дифференциальные уравнения неравномерного плавноизменяющегося движения в призматических руслах
В призматических руслах площадь живого сечения потока может изменяться только за счет изменения глубины и поэтому при подстановке в формулу (6.56) условия dω/dl=0 получаем дифференциальное уравнение неравномерного плавноизменяющегося движения для призматических русл с положительным уклоном дна:

Вводя в уравнение (6.57) параметр кинетичности
и используя понятие расходной характеристики 

Выражая расход Q по формуле Шези через расходную характеристику К0, соответствующую нормальной глубине h0 в канале при заданном уклоне i0, можем записать
Наконец, используя понятие гидравлического показателя русла

получаем уравнение неравномерного движения в призматических каналах только правильной формы:

Для призматических русл с горизонтальным дном (i0=0) получаем

Для русл с обратным уклоном (i0 0 при равенстве нулю числителя уравнения (6.58) получаем

что соответствует постоянству глубины потока вдоль русла, т. е. равномерному движению (h=h0). Последнее следует также непосредственно из выражения (6.63), которое представляет собой формулу Шези 
Для русл с горизонтальным дном равенство нулю числителя уравнения (6.61) и, следовательно, производной (6.61) возможно либо при Q=0, либо при К=∞ (или h=∞). Оба условия не имеют смысла, поскольку перестает существовать движение жидкости.
При обратном уклонe дна равенство (6.64) может быть получено из уравнения (6.62), если
Поскольку отрицательный знак уклона дна русла учтен при выводе уравнения (6.62), в последнем выражении знак «-» относится к расходной характеристике К, что также лишено смысла.
Таким образом, получено подтверждение, что при уклонах дна i0=0 и i0 
т. е. кривая свободной поверхности неравномерного потока пересекает линию К-К под углом 90°. При этом существенно увеличивается кривизна линий токов и поток становится резко неравномерным.
Поэтому результат (6.65), полученный из уравнений (6.58)-(6.62), справедливых для плавноизменяющегося движения, не является строгим. В действительности линия К-К пересекается свободной поверхностью потока под углом, несколько меньшим, чем прямой. Если это пересечение происходит при уменьшении глубин от h1>hK до h2 0 и, следовательно, dh/d/>0: кривая свободной поверхности, глубины которого возрастают вниз по течению, называется кривой подпора. Если же глубины потока по течению уменьшаются (рис. 6.22, б), т. е. h2 0 могут быть случаи i0 iK, i0=iK. Линиями нормальной N-N и критической K-К глубины выделяются три характерные области (диапазона) изменения глубины неравномерного потока: область а, где h>h0 (при i0 hK (при i0>tK); область b, где h0>h>hK (при i0 iK — область отсутствует при i0=iK. (когда h0=hK), область с, где h iK).
Знак производной dhldl, т. е. образование кривой подпора или спада на участке неравномерного движения, определяется знаками числителя и знаменателя правой части уравнения (6.59). При h>h0 числитель будет положительным 1-(K0/К) 2 >О, поскольку при этом K>К0. При h 2 hк согласно уравнениям Пк 0. При h 1 и 1-Пк 0, из чего следует, что в указанных областях свободные поверхности являются кривыми подпора. При разных знаках — в области b — производная отрицательна и свободная поверхность в русле образует кривые спада.
Форма кривых подпора и спада в каждой области определяется тем, как стремится глубина неравномерного потока к линиям N-N и К-К, т. е. условиями (6.64) и (6.65) на границах областей (табл. 6.3).
Уклон дна канала меньше критического.
Линия нормальных глубин N-N при i0 h0>hк свободная поверхность представляет кривую подпора. При стремлении глубины потока к нижнему пределу глубин (h→h0) свободная поверхность (линия а1) в верхней части участка неравномерного движения асимптотически приближается к линии N-N. При стремлении глубины к верхнему пределу (h→∞) расходная характеристика К→∞ и величина (К0/К) 2 →0; параметр кинетичности Пк→0. Следовательно, при h→∞ производная dhldl→i0=const. Поскольку дно русла по отношению к горизонтальной плоскости имеет уклон i0 и глубины измеряются от наклонной плоскости дна, равенство dh/dl=i0 характеризует горизонтальную прямую п-п (рис. 6.23). При увеличении глубины (h→∞) свободная поверхность асимптотически приближается сверху к горизонтальной прямой п-п, т. е., несмотря на увеличение глубины потока, отметки свободной поверхности вниз по течению уменьшаются. Таким образом, свободная поверхность имеет вогнутую форму и называется кривой подпора a1 (табл. 6.3).
Такого типа кривые подпора образуются в тех случаях, когда на пути равномерного потока в русле с i0 h>hK устанавливается кривая спада b1 (табл. 6.3). Поскольку к линии N-N кривая стремится снизу асимптотически, а к линии К-К сверху условно под прямым углом, она имеет выпуклую форму.
Эта кривая может наблюдаться в каналах с уклоном i0 iк располагается ниже линии К-К.
В области а при h>hк>h0 в русле устанавливается кривая подпора а2 (табл. 6.3). Нижний предел глубины h=hк соответствует условию (6.65), т.е. гидравлическому прыжку. При стремлении глубины к верхнему пределу (h→∞) свободная поверхность неравномерного потока будет асимптотически снизу приближаться к горизонтальной прямой п- п, поскольку при этом dhldl→i0. Следовательно, кривая свободной поверхности имеет выпуклую форму.
Эта кривая образуется, например, за гидравлическим прыжком перед препятствием в виде сооружений мостового перехода, трубы или плотины (между сечениями 1-1 и 2-2), устанавливаемыми в русле с уклоном дна i0>iк (рис. 6.24).
Теоретически длина кривой спада b2 равна бесконечности, в практических расчетах ее длину находят, ограничивая сечением 2-2, в котором глубина h2=(1,005-1,05) h0.
В области с русла при h iK (см. рис. 6.19), если на предыдущем участке канала значение уклона было еще большим (i01>iK).
При определении длины кривой подпора с2 в практических расчетах глубину потока в сечении 2-2 принимают в зависимости от точности расчета, на 0,5-5% меньше нормальной глубины: h2=(0,995-0,95)h0, условно считая, что ниже этого сечения движение становится равномерным.
Критический уклон дна канала.
В областях а и с производная dhldl >0, из чего следует, что глубины потока вниз по течению возрастают (см. табл. 6.3).
Форма свободной поверхности потока при этом может быть установлена путем преобразования дифференциального уравнения неравномерного движения (6.57). Расход в числителе правой части уравнения при iо=iк может быть выражен через параметры потока при равномерном движении: 

Если допустить, что Вк≈χк и В≈χ (это можно считать приемлемым для широких и неглубоких русл), то получаем

Следовательно, как в области а, так и в области с в рамках принятых допущений устанавливаются горизонтальные прямые подпора а3 и с3.
Прямая подпора а3 образуется, например, в канале (рис. 6.26) с уклоном i02>iK, если к нему примыкает канал с меньшим уклоном (i03 iK.


В начальном сечении 1-1 в этом случае h1=h01, а в конечном сечении 2-2 глубина h2=hк. Длина прямой подпора с3 при этом находится аналогичным образом:

Русло с горизонтальным дном.
В этом случае равномерное движение существовать не может и линия нормальных глубин N- N отсутствует (см. табл. 6.3). Линия критической глубины К- К выделяет две области b и с.
В области b при h>hK согласно уравнению (6.61) имеем выпуклую кривую спада b0, заканчивающуюся водопадом. При h hK), анализируя уравнение (6.62), аналогично тому, как это было выполнено в отношении уравнения (6.61), для i0=0 и принимая во внимание, что при выводе уравнения (6.62) отрицательный знак уклона дна уже был учтен, получаем кривую спада b‘ выпуклой формы (табл. 6.3).В области с (h
Плавноизменяющееся движение
При движении жидкости в естественных руслах обычно живое сечение непрерывно изменяется вдоль потока как по форме, так и по площади, и движение жидкости является установившимся неравномерным. Для облегчения изучения такого движения в гидравлике введено понятие «плавноизменяющееся движение», которое характеризуется следующими свойствами:
— кривизна линий тока в потоке считается весьма незначительной;
— угол расхождения между отдельными линиями тока очень мал;
— живые сечения потока являются плоскими сечениями, нормальными к оси потока.
Если внутри плавно изменяющегося потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения, то вследствие того, что скорости и ускорения почти перпендикулярны живому сечению, силы инерции в уравнение равновесия не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения ничем не будут отличаться от закона распределения давления в жидкости, находящейся в покое. Отсюда следует четвертое важное свойство плавно изменяющегося движения:
— при плавноизменящемся движении давление по живому сечению распределяется по гидростатическому закону, т.е. по закону прямой линии.
Если эти четыре свойства не выполняются, то движение называется резкоизменяющимся.
Дифференциальные уравнения движения жидкости (уравнения Эйлера)
При рассмотрении движения жидкостей наблюдается целый ряд новых переменных, которых не было при рассмотрении жидкости в равновесии.
Основной переменной является время 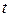
В общем случае на жидкость действуют силы массовые 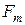
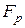
Обозначая проекции на оси координат ускорений объемных сил через 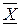
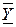
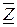
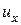
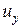
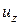
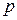
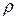
Задача гидродинамики — установить зависимости этих величин от координат времени 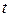
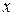
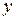
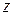
Выведем основные дифференциальные уравнения, устанавливающие эту зависимость. Выделим в движущейся жидкости элементарно малый объем в форме параллелепипеда.
Воспользуемся полученными ранее (Тема: “Дифференциальные уравнения равновесия жидкости”) уравнениями равновесия. К действующим на элементарный параллелепипед силам присоединим также силы инерции.
Сумма проекций всех сил на ось 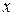
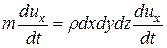
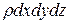
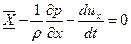
Составляя аналогичные уравнения относительно осей 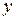
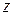
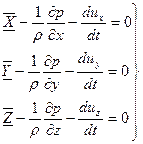
Так как 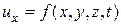
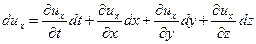
Разделив все члены этого полного дифференциала на 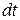
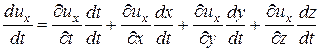
аналогично можно представить
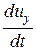
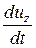
Производные от координаты движущейся точки по времени представляют собой соответствующие проекции ее скорости. Подставляя производные в уравнение и перенеся члены, содержащие скорость, в правую часть, получим систему общих дифференциальных уравнений движения жидкого тела (Эйлер, 1755г.):
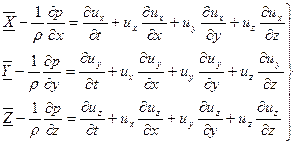
http://studizba.com/lectures/154-stroitelstvo/2463-gidravlicheskie-osnovy-rascheta-sistem-vodosnabzhenija-i-vodootvedenija/45874-32-differencialnye-uravnenija-ustanovivshegosja-neravnomernogo-plavno-izmenjajuschegosja-dvizhenija-zhidkosti.html
http://helpiks.org/3-34534.html













