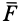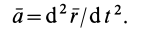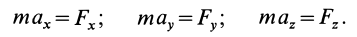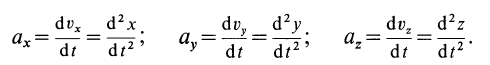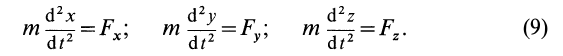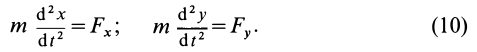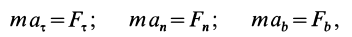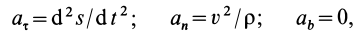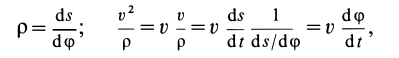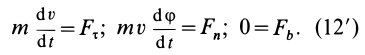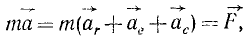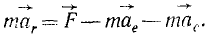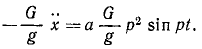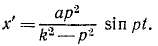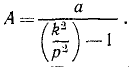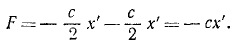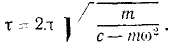Дифференциальное уравнение в физике пример
Примеры решения задач по механике, требующих интегрирования дифференциальных уравнений
(Задачи взяты из задачника: И.В. Мещерский «Сборник задач по теоретической механике», М.: Наука, 1981г., 460с.)
Задача №1. Пример задачи, приводящей к интегрированию дифференциальных уравнений методом разделения переменных.
При движении тела в неоднородной среде сила сопротивления изменяется по закону 
Будем считать, что движение происходит вдоль оси 0Х, и что при t =0 тело находилось в начале координат, тогда проекция на ось 0Х силы, действующей на тело, может быть записана в виде

С учётом этого выражения, имеем следующее уравнение движения (считая массу тела m =1 кг)

которое дополняется начальными условиями


Решение уравнения второго порядка (1) можно свести к двум последовательным интегрированиям дифференциальных уравнений первого порядка. Чтобы получить первое уравнение, перепишем (1) в виде:

и домножим на dt левую и правую части (3), учитывая при этом, что dx = vxdt , получим:


Это уравнение с разделяющимися переменными (вида (1.5) из Раздела №1 Части I ). Очевидно, что оно, дополняется начальным условием, следующим из (2):

Разделив переменные в (4), в соответствие с формулой (1.7):

вычисляя данные интегралы, получим частный интеграл уравнения (4) (в форме (В.4) из Введения к Части I ):

Выразив отсюда vx , будем иметь частное решение уравнения (4) (в форме (В.6) из Введения к Части I ):

Заменяя теперь в (7)

мы снова получаем уравнение с разделяющимися переменными (вида (1.1) из Раздела №1 Части I )

Разделяя в (8) переменные, с учётом начального условия (2), ищем частный интеграл этого уравнения (в виде (1.4) из Раздела №1 Части I ):

Вычисляя интегралы в (9), получим:

— частный интеграл уравнения (8) в форме (В.4) из Введения к Части I. Выражая отсюда x , получим частное решение уравнения (8):

которое одновременно является и частным решением уравнения движения (1), удовлетворяющим начальным условиям (2), то есть, представляет собой закон движения тела (координата x , (или в данном случае путь), как функция времени). Таким образом, решение исходного уравнения движения второго порядка (1) в процессе решения задачи было сведено к интегрированию двух уравнений первого порядка с разделяющимися переменными (4) и (8).
Задача №2. Пример задачи, приводящей к интегрированию линейного обыкновенного дифференциального уравнения первого порядка.




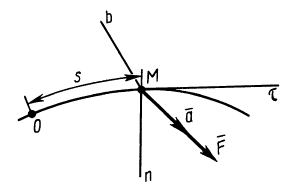
Спроектируем данное равенство на направление движения и перпендикулярное ему. Эти направления указаны на рисунке векторами 


Здесь учтено, что центростремительное ускорение


Сделаем в первом уравнении в (1) замену переменной — перейдем от дифференцирования по времени к дифференцированию по углу 


С учетом этой замены перепишем (1):

Домножая второе уравнение на 

Это уравнение типа (2.1) (из Раздела №2 Части I ), в котором независимой переменной вместо t является 



Уравнение (3) дополняется начальным условием:

С учетом указанных обозначений, используя формулу (2.9) (из Раздела №2 Части I ), решение уравнения (3) можно записать в виде:

Вычисляя с помощью интегрирования по частям интервалы в (5) , окончательно получим:

По условиям задачи тело должно остановиться на поверхности; т.е. при каком-то угле 

Подставляя вместо 


Значение угла 


то из уравнений (2) получим:

Отсюда: 


из (7) будем иметь:

Следовательно, чтобы тело остановилось на шероховатой поверхности цилиндра, нужно, чтобы его начальная скорость 

Задача №3. Пример задачи, приводящей к решению линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Выберем начало координат в положении статического равновесия тела и расставим силы, действующие на тело в процессе колебаний (считаем, что тело в данный момент времени движется вверх). Если АВ обозначает длину нерастянутой пружины, то отрезок ОВ представляет статическое удлинение пружины под действием силы mg . По закону Гука mg = k × ОВ, где k — коэффициент жёсткости пружины. Записываем второй закон Ньютона:

Проектируем это равенство на ось ОХ, учитывая, что


В результате получим уравнение колебаний


где 

Уравнение (1) представляет собой однородное обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами (уравнение (1.1) Части II ). Для его решения используем схему, описанную в Разделе №1 Части II .
Составляем характеристическое уравнение:

Вычисляем дискриминант уравнения (2):

Поскольку в данном случае, в соответствие с условиями задачи движение тела носит колебательный (периодический) характер, то его координата должна изменяться со временем по гармоническому закону, то есть по закону косинуса или синуса. Для того же, чтобы решение уравнения (1) выражалось через данные функции, мы должны считать, что D 
где величины 



В случае отсутствия затухания (когда n =0), 

Если же n ¹ 0, то период колебаний, с учётом (5),:

Выражаем отсюда 
Подставляя данные задачи, получим a =19 
В соответствие со своим определением, логарифмический декремент затухания есть натуральный логарифм отношения двух последовательных амплитуд, (то есть взятых через половину периода колебания 


Задача №4. Пример задачи, приводящей к решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.



Направим ось 0 X вдоль направления движения, выбрав начало координат в положении статического равновесия тела. При этом считаем, что сила тяжести скомпенсирована силой статического сжатия пружины амортизатора. Записываем второй закон Ньютона:

Проектируем это равенство на ось ОХ, учитывая, что



В результате получим уравнение колебаний


где обозначено 

При колебаниях на фундамент действует сила, складывающаяся из силы деформации пружины и силы сопротивления, равная в соответствие с третьим законом Ньютона,

Следовательно, для вычисления этой силы нужно знать уравнение движения тела 

Обозначим для краткости записи через 
Приравнивая коэффициенты при 

Решая данную систему, находим


Подставим (4) в (3):

Данную формулу, обозначая


можно переписать в виде:

Подставим теперь (7) в (2):



формулу (8) можно переписать в виде

Отсюда следует, что максимальное динамическое давление всей системы на фундамент равно

Классическая механика: о диффурах «на пальцах»
Введение
В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…
Физический смысл
В своей статье про Фильтр Калмана я описал что такое уравнения вида «вход-выход», передаточная функция и операторная форма записи дифференциальных уравнений (см. раздел «Основные понятия» в [2]). Примером части математической модели динамического объекта в операторной форме записи может служить следующее уравнение:
(1)
Это распространенная упрощенная модель динамических систем. Опережая напишу, что модель тела в движке «Farseer» использует урезанный аналог представленной выше модели (динамического звена второго порядка). Ниже представлено описание принятых в ней обозначений.
- а0, а1, а2 — коэффициенты инерции, демпфирования и жесткости, соответственно.
- b0, b1 — коэффициенты входного воздействия.
- s — оператор Лапласса (d/dt).
- α(s), β(s) — выходная и входная переменные, как функции оператора Лапласса.
Представленное уравнение описывает динамическую систему типа «один вход — один выход» (SISO). Ее можно использовать для описания динамики объекта по одной из его степеней свободы. Как Вам, возможно, известно, у свободного тела есть шесть степеней свободы — три поступательные (линейное движение вдоль трех осей системы координат (СК) ) и три вращательные (повороты вокруг осей СК). Таким образом, полная модель физического тела будет описываться шестью такими уравнениями (или четырьмя для 2D случая). Вы сразу можете сказать, что уже это свидетельствует о слишком высокой сложности такого подхода. Но на самом деле в Farseer, к примеру, класс тела (Body) содержит и линейные координаты тела (по сути это пара α(s) по OX и OY), и линейные скорости (пара s*α(s) по OX и OY) и параметры ориентации и угловой скорости. Эти параметры обсчитываются раздельно для каждой из осей, т.е. количество уравнений такое же — два уравнения по оси OX (линейное и угловое движение) и два для оси OY. Разница лишь в форме уравнений.
Алгоритм в движке Farseer — приближенный и упрощенный, но позволяет работать с варьируемыми квантами времени. В функцию обсчета параметров движения (Island.Solve(ref TimeStep step, ref Vector2 gravity)) передается время, прошедшее после последнего обсчета параметров. Это позволяет при недостаточной производительности компьютера держать скорость течения игрового времени примерно постоянным в ущерб плавности и реалистичности движения игровых объектов.
При построении дискретной модели на основе диференциальных уравнений мы четко завязываемся на фиксированный квант времени. Уравнения интегрируются для изначально заданной частоты дискретезации, и если с момента последнего обсчета по какой-то причине прошло времени больше, чем заданный квант (в англоязычной литературе его называют «time sample»), то мы либо должны произвести обсчет несколько раз, либо получим замедление движения объекта. Последнее я как раз и наблюдал в игре «Command Cortex» на слабой машине. Движения акторов были плавными но медленными (акторы, управляемые человеком, получают преимущество). Таким образом, нельзя говорить об исключительном преимуществе одного из этих подходов.
Теперь о том, за что отвечают коэффициенты представленного выше уравнения. Это уравнение описывает движение физического тела относительно положения равновесия при α(s) = 0. Это еще одна из причин кажущегося неудобства применения такой модели в игровой механике. При отсутствии приложенных внешних сил данная модель рано или поздно возвратит (при условии устойчивости модели) тело в положение равновесия. Представьте игровой мир, наполненный шариками, которые все время стремятся в начало координат (например, в левый верхний угол экрана). К такому поведению приводит наличие коэффициента жесткости (см. а2 выше). Представьте, что тело соединено с началом координат пружиной. Пока на тело действуют силы, пружина растянута, но стоит убрать внешнее воздействие и тело устремится к нулю. Тела в движке Farseer таким поведением не обладают. Если мы зададим коэффициент a2 равным нулю, то и в данном случае тела не будут стремиться к началу координат (см. выше я писал, что модели в Farseer по сути урезанные варианты этой модели). Ну и зачем этот коэффициент тогда нужен, спросите Вы. Если раскрыть скобки в левой части уравнения (1) и вместо слагаемого
a2*α(s)
напишем
a2*(α(s) — α0)
то через α0 мы получим возможность задать положение, к которому игровой объект будет стремиться. Величина коэффициента а2 отвечает за то, насколько быстро тело переместится в заданное положение равновесия (чем больше значение, тем выше жесткость пружины). Как такое реализовывается в Farseer я пока не выяснил, но думаю придется создать дополнительный источник воздействия.
Теперь коэффициент a1. Это коэффициент демпфирования. Чем больше значение этого коэффициента, тем быстрее гасится скорость (линейная или угловая). Аналогия из жизни — вязкие жидкости, такие как масло, мед, эпоксидная смола. Эти жидкости очень вязкие (имеют большое значение коэффициента демпфирования). Чем выше скорость движения тела в них, тем выше сопротивление этому движения. Если медленно двигать в них ложку, например, то преодолеть сопротивление большого труда не составит, а вот если ударить с размаху, то удар будет жестким.
Величина коэффициента а0 характеризует инерцию объекта. При описании линейного движения в качестве коэффициента а0 используется масса. Чем выше его значение, тем медленнее тело набирает скорость при приложении к нему внешних сил.
Теперь о коэффициентах в правой части уравнения (1). Тут нужно заметить, что данная модель расширенная на случай, когда входное воздействие определяется не только самим значением внешней силы, но и ее изменением. Для описания динамики игровых объектов это, возможно, будет излишним. Однако в промышленных системах управление встречаются и такие модели. Каков же их физический смысл? Коэффициент b1 это по сути коэффициент передачи внешней силы вовнутрь объекта. Обычно он равен еденице, т.е. сила передается как есть.
Коэффициент b0 интересен. Он играет роль форсирующего коэффициента. Представьте очень инерционный объект, к которому прикладывают силу, плавно нарастающую со временем. Если скорость нарастания и конечная величина силы будут малы, то объект очень медленно набирать скорость. Но если силу сделать большой, то после достижения внешней силой заданного значения объект не остановится в каком-то положении, а будет колебаться под действием инерции. Форсирование — это воздействие, пропорциональное скорости нарастания внешней силы. Если мы выберем его большим, то даже при малой скорости нарастания внешней силы наш объект будет достаточно быстро набирать скорость, а когда внешняя сила достигнет заданного значения, форсирование отключится. Вот такой вот хитрый этот «b0».
Динамика в картинках
Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])
Transfer function «w» from input «u1» to output…
y1: (s + 1)/(s^2 + s + 1)
Continuous-time model.
========================================= 

Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).
Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)
>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице. 

Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.
Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)
>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1) 

Сразу вывод: больше вязкость — быстрее затухают колебания.
Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)
>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1) 

Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.
Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)
>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1) 

Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).
И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)
>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1) 

Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.
На правах PS
В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.
Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
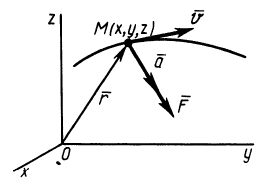
Из кинематики точки известно, что ускорение 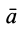
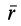
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 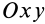
Так как 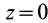
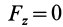
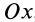
Так как при движении 
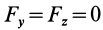
где 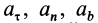
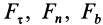
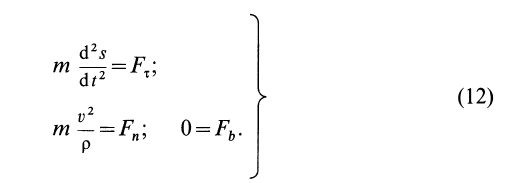
где 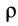
Второе уравнение из (12) можно преобразовать:
где 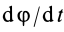
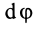
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 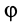
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
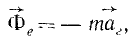
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
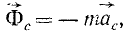
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
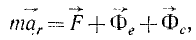
или в проекциях на оси координат:
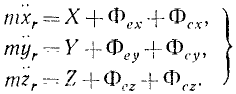
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
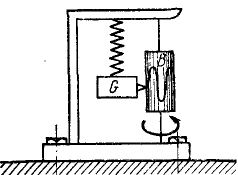
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 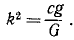
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 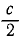
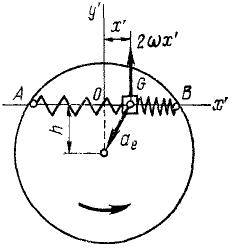
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 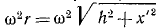
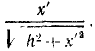
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 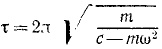
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://habr.com/ru/post/135794/
http://www.evkova.org/differentsialnyie-uravneniya-dvizheniya-materialnoj-tochki-v-teoreticheskoj-mehanike