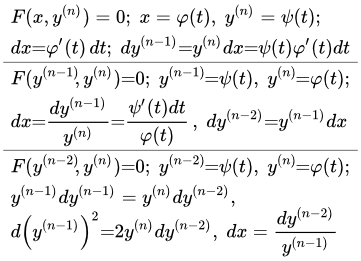Дифференциальное уравнение второго порядка с квадратом производной

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Здесь рассмотрены методы решения дифференциальных уравнений высших порядков, решаемые в квадратурах, то есть решения которых можно выразить через конечное число интегралов. К таким уравнениям относятся следующие типы:
⇓
⇓
⇓
Также приводятся подробно разобранные примеры решений ⇓ таких уравнений.

F(x, y (n) ) = 0: Дифференциальные уравнения, содержащее только независимую переменную и производную n-го порядка

Рассмотрим дифференциальное уравнение высшего порядка, содержащее только независимую переменную x и производную n-го порядка :
(1) .

y (n) = f(x) Разрешенные относительно старшей производной

Если уравнение (1) удастся разрешить относительно производной, то есть представить в виде
(1.1) ,
то оно решается непосредственным интегрированием.

x = f(y (n) ) Разрешенные относительно независимой переменной

Рассмотрим случай, когда уравнение (1) можно разрешить относительно переменной x . В этом случае, независимая переменная является функцией от старшей производной:
(1.2.1) .
Это уравнение можно решить в квадратурах в параметрическом виде, последовательно понижая порядок.

Вводим параметр t :
(1.2.2) .
Тогда из (1.2.1) получаем:
(1.2.3) .
При переходе к параметрическому виду (1.2.2) – (1.2.3), независимой переменной становится параметр t , а переменные и x – зависимыми от параметра t .

Возьмем дифференциал от (1.2.3):
;
(1.2.4) .
Выразим производную n-го порядка через производную порядка n–1 , воспользовавшись уравнением:
.
Учитывая (1.2.2), и подставляя (1.2.4), находим выражение дифференциала производной n–1 — го порядка через параметр t :
.

Интегрируя, получаем выражение производной n-1 — го порядка через параметр t :
(1.2.5) .
Это уравнение, вместе с (1.2.3), дает выражение производной меньшего порядка в параметрическом виде:

Далее выражаем дифференциал производной порядка n – 2 :
.
Подставляя (1.2.4) и (1.2.5), получаем дифференциал, выраженный через параметр t . После чего интегрируем по t , и, вместе с уравнением , получаем выражение производной в параметрическом виде. И так далее, пока получим зависимость функции y от параметра t .

F(x, y (n) ) = 0 Общий случай

Теперь рассмотрим дифференциальное уравнение высшего порядка, содержащее только старшую производную и независимую переменную в общем случае:
(1.3.1) .
Это уравнение можно разрешить в квадратурах, если удастся представить уравнение (1.3.1) в параметрическом виде. То есть если удастся подобрать такие функции , для которых
(1.3.2) ,
и при этом уравнение (1.3.1) окажется эквивалентным уравнениям
(1.3.3) .

Тогда уравнение можно решить в квадратурах. Для этого сначала выразим дифференциал независимой переменной x через параметр t , используя первое уравнение (1.3.3):
.
После этого выражаем через параметр t дифференциал производной n-1-го порядка:
.
Интегрируя это уравнение по переменной t , получаем выражение для производной n-1-го порядка в параметрическом виде:
.
Где .

Далее выражаем через t дифференциал производной n-2-го порядка:
.
Интегрируя, получим параметрическое представление производной n-2-го порядка. И так далее, пока получим параметрическое представление функции y .

F(y (n-1) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-1

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
(2.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(2.1.2) .
Тогда если положить
(2.1.3) ,
то уравнение (2.1.1) будет выполняться автоматически. При этом должно соблюдаться еще одно условие – чтобы представления (2.1.1) и (2.1.3) были эквивалентными. То есть, чтобы при переходе от одного представления к другому, не появились новые и не терялись существующие решения.

Если найдено такое параметрическое представление уравнения (2.1.1), то его можно решить в квадратурах. Для этого, как и в предыдущем случае, сначала выразим дифференциал независимой переменной x через параметр t . Преобразуем первое уравнение (2.1.3):
.
Отсюда
;
(2.1.4) .
Интегрируя, получаем выражение независимой переменной x через параметр t :
(2.1.5) .

Тем же способом, что и в предыдущем случае, выражаем производные и меньших порядков через t :
.
Интегрируем:
.
Продолжая процесс, получаем выражения остальных производных и самой функции y через параметр t . Вместе с уравнением (2.1.5), это дает решение исходного уравнения в параметрическом виде.

y (n-1) = f(y (n) ) Разрешенные относительно младшей производной

Рассмотрим частный случай уравнения (2.1.1), в котором производная меньшего порядка выражена через старшую производную:
.

Это уравнение интегрируется в квадратурах, введением параметра
.
Тогда
.
Из этих уравнений
;
;
;
.

Тем же способом находим выражение через t производных и переменной y .

y (n) = f(y (n-1) ) Разрешенные относительно старшей производной

Рассмотрим второй частный случай, когда старшая производная выражена через производную меньшего порядка:
(2.3.1) .

Если уравнение (2.3.3) удастся разрешить относительно t , то получим зависимость вида . Учитывая (2.3.2), получаем уравнение, в котором производная n–1-го порядка является функцией от независимой переменной:
.
Интегрируя это уравнение n–1 раз, получим зависимость y от x . См. Дифференциальное уравнение y (n) = f(x)

Но в любом случае можно получить решение в параметрическом виде.
;
.

Тем же способом находим выражение через t производных и переменной y .

F(y (n-2) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-2

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
(3.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(3.1.2) .
Положим
(3.1.3) .
Тогда уравнение (3.1.1) выполняется автоматически. Считаем также, что представления (3.1.1) и (3.1.3) эквивалентны.

Для решения уравнения запишем дифференциалы производных порядков n-1 и n-2 :
.
Исключаем dx . Из второго уравнения
(3.1.4) .
Подставим в первое и преобразуем:
;
;
.
Подставляя (3.1.3) и интегрируя, получим выражение производной через параметр t :
;
;
;
.
Знак плюс или минус выбирается из начальных условий, как и постоянная интегрирования .

Из (3.1.4) находим выражение x через t :
(3.1.5) ;
(3.1.6) .

Далее, как и в предыдущих случаях находим выражения производных и зависимой переменной y через t . Например,
;
;
и так далее.

Примечание. В литературе иногда не ставят знак плюс-минус. При этом подразумевают, что корень является многозначной функцией и автоматически может быть как положительным, так и отрицательным.

y (n) = f(y (n-2) ) Разрешенные относительно старшей производной

Сведем к квадратурам уравнение, разрешенное относительно старшей производной:
(3.2.1) .

Для упрощения выкладок введем новую переменную:
(3.2.2) .
Тогда исходное уравнение (3.2.1) станет уравнением второго порядка:
(3.2.3) .
Умножим его на и выделим полную производную:
;
.
Отсюда получаем первый интеграл:
.

Находим выражение для дифференциала . Для этого извлекаем квадратный корень:
.
Отсюда
(3.2.4) .
Знак плюс или минус выбирается из начальных условий. В общем решении допустим любой знак.

Интегрируя, получаем зависимость u от x в неявном виде:
(3.2.5) .
Если после интегрирования удастся разрешить u относительно x , то, поскольку , мы получим уравнение вида (1.1), которое решается последовательным интегрированием.

Если уравнение (3.2.5) разрешить относительно u не удастся, то решаем в параметрическом виде, как это описывалось ранее. То есть вводим параметр . Тогда (3.2.5) и (3.2.4) дают выражения переменной x и ее дифференциала через t :
(3.2.6) .
(3.2.7) .
Далее, уравнение

вместе с (3.2.7) дают параметрическое представление зависимости производной порядка n — 2 от переменной x .

Используя (3.2.6), можно найти параметрическое представление остальных производных и самой функции y от переменной x . Например,
;
.
И так далее.

Примеры решений задач

Все примеры Далее рассматриваются примеры с подробными решениями следующих дифференциальных уравнений.
⇓
⇓
⇓
⇓
⇓

Пример 1

Найти общее решение дифференциального уравнения третьего порядка, содержащего только старшую производную и независимую переменную.
(П1.1) .

По всей видимости, в уравнении (П1.1) выразить через x в элементарных функциях или не возможно, или довольно сложно. Мы не будем пытаться это делать, поскольку здесь независимая переменная x выражена через производную . Поэтому решаем задачу в параметрическом виде.

Вводим параметр t . Получаем параметрические уравнения, эквивалентные (П1.1):
(П1.2) .

Выразим дифференциал переменной x через параметр t :
;
(П1.3) .

Используя (П1.2) и (П1.3), выражаем дифференциал производной второго порядка через параметр t :
.
Интегрируем.
;
(П1.4) .

Используя (П1.3) и (П1.4), аналогично предыдущему имеем:

;

.

Пример 2

Найти частное решение дифференциального уравнения второго порядка, содержащее только вторую производную и независимую переменную:
(П2.1) ;
(П2.2) .

Это уравнение является кубическим по отношению ко второй производной , и уравнением седьмой степени (если умножить его на x ) по отношению к независимой переменной x . Можно попытаться разрешить его относительно или x , но здесь есть более простой способ.

Заметим, что уравнение (П2.1) выполняется, если выразить зависимость от x , определяемую уравнением (П2.1) в параметрическом виде:
(П2.3) .
Действительно, подставляя (П2.3) в (П2.1) получаем:
;
;
.
То есть если взять параметрическое представление (П2.3), то уравнение (П2.1) выполняется.

Однако это не означает, что представление (П2.3) автоматически эквивалентно уравнению (П2.1). Поскольку кубическое уравнение может иметь три действительных корня, то, возможно, уравнение (П2.3) можно представить в параметрическом виде тремя неэквивалентными способами. Также возможен случай, когда условия теоремы существования и единственности решения дифференциального уравнения не выполняются, и заданным начальным условиям будут удовлетворять несколько решений. Все это нужно иметь в виду при решении подобных уравнений. Но нам нужно найти любое решение, удовлетворяющее заданным начальным условиям. Поэтому попробуем применить для этой цели представление (П2.3).

Выразим дифференциал независимой переменной x через дифференциал параметра t , используя (П2.3):
.
Выразим дифференциал производной через параметр t и его дифференциал:
.
Интегрируем:
. Найдем значение постоянной , используя первое начальное условие (П2.2). Из (П2.3) находим: . При . При . Отсюда .

Итак, мы нашли параметрическое представление для производной:
.
Аналогично предыдущему, выражаем y через параметр t :
;

.
Находим значение постоянной , используя второе начальное условие (П2.2). При . При . Отсюда .

Тем самым мы нашли частное решение в параметрическом виде:
.
Выразим t через x .
;
.

Пример 3

Решить дифференциальное уравнение, содержащее только производные первого и второго порядков:
(П3.1) .

Нетрудно видеть, что если положить
(П3.2) ,
то уравнение (П3.1) выполняется автоматически. Поэтому решаем это уравнение в параметрическом виде.

Выразим дифференциал независимой переменной x через параметр t .
;
;
(П3.3) .

Интегрируя (П3.3), получаем выражение независимой переменной x через параметр t :
;
(П3.4) .

Используя формулу , и применяя выражение через t (см. (П3.2)), выразим дифференциал dy через t :
.

Интегрируя, находим выражение зависимой переменной через параметр t :
.

Итак, мы нашли зависимость в параметрической форме:
.
Отсюда можно получить зависимость y от x в явном виде. Из второго уравнения, . Подставляем в первое:
.

Пример 4

Решить дифференциальное уравнение, содержащее только производные второго и третьего порядков:
(П4.1) .

Это дифференциальное уравнение содержит только производные второго и третьего порядков. При этом оно разрешено относительно высшей производной. Решаем параметрическим методом. За параметр t возьмем производную второго порядка:
(П4.2) .

Выразим дифференциал независимой переменной x через параметр t . Из (П4.1) имеем:
;
;
(П4.3) .

Выразим независимую переменную x через параметр t . Для этого интегрируем (П4.3):
;
(П4.4) .
См. Обратные гиперболические функции, их графики и формулы

Выразим дифференциал через параметр t и, интегрируя, выразим производную через t :
;
;
(П4.5) .

Выразим дифференциал зависимой переменной y через параметр t . После чего интегрируя, выразим y через t :
;
;
(П4.6) .

Исключим параметр t из уравнений (П4.4) т (П4.6).
;
.

Примечание.
Эту задачу можно решить проще, если с самого начала выбрать следующее параметрическое представление для производных:
.

Пример 5

Решить дифференциальное уравнение с заданными начальными условиями:
(П5.1) ;
(П5.2) .

Уравнение имеет вид (3.2.3). В нем вторая производная выражена через функцию (зависимую переменную y ). Решаем изложенным выше методом ⇑.

Умножим исходное уравнение (П5.1) на и выделяем полный дифференциал.
;
;
;
.
Извлекаем квадратный корень:
(П5.3) .

Найдем значение постоянной и знак корня из начальных условий (П5.2). Для этого подставляем в (П5.3) :
.
Отсюда видно, что нужно взять знак плюс и . Тогда
.

Разделяем переменные и интегрируем.
;
;
;
(П5.4) .

Определяем значение постоянной . Для этого подставляем значения начальных условий (П5.2): :
.
Отсюда . Подставляем в (П5.4):
.

Возводим в квадрат и выполняем преобразования:
;
.
Извлекаем квадратный корень:
.
Выбираем знак плюс или минус из начальных условий (П5.2). Подставляем :
.
Этому уравнению удовлетворяет знак плюс. Тогда
.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 11-05-2021

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Дифференциальное уравнение второго порядка с квадратом производной

Линейным называется дифференциальное уравнение n -го порядка , если оно 1-ой степени относительно искомой функции y ( x ) и ее производных , то есть имеет вид:

Если коэффициент P ₀ ( x ) ≠ 1, то на него можно поделить и после соответствующих переобозначений получить:

Уравнение (8.43) называется уравнением с переменными коэффициентами. Предположим, что в нем функции , непрерывны на интервале . Тогда для уравнения (8.43) на данном интервале имеет место задача Коши, сформулированная нами ранее.

Примечание. Частным случаем (8.43) является линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами:

Если в уравнении (8.43) f ( x ) ≡ 0, то оно называется однородным, если f ( x ) ≠ 0, то неоднородным.

Теорема 8.3 (о структуре общего решения линейного неоднородного ДУ). Общее решение линейного неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного и некоторого частного решения неоднородного уравнения . Запишем коротко:

Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (8.43), имеет вид:

Пусть в уравнении (8.45) функции . Тогда оно принимает вид:

и называется линейным однородным дифференциальным уравнением n -го порядка с постоянными коэффициентами , где – функции, n раз дифференцируемые.

Рассмотрим решения уравнений (8.45) и (8.46). Обозначим полную совокупность их линейно независимых решений через . Тогда, по свойству решений однородного уравнения, их линейная комбинация также является решением уравнения (8.45) и (8.46), т о есть общее решение может быть записано в виде:

где c_i – константы интегрирования.

Перейдем к конструированию функций . Какого они вида? Так как эти функции в уравнениях (8.45) и (8.46) n раз дифференцируемы, то их конструкция при дифференцировании не меняется. Это возможно в случае экспоненциального вида функций, то есть при

где , . Отсюда, линейная комбинация функций (8.48):

– также решение уравнений (8.45) и (8.46).

Рассмотрим одну из функций (8.48) – функцию y = e λx как решение для уравнения (8.46) с постоянными коэффициентами. Продифференцируем ее n раз:

Так как e λx ≠ 0 , то ( 8.50)

–алгебраическое уравнение n -ой степени относительно λ, называемое характеристическим уравнением для уравнения (8.46). Известно, что уравнение n -ой степени имеет равно n корней как действительных, так и комплексных, с учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений числа λ, ранее обозначенных нами через , которые при подстановке в (8.49) приводит нас к окончательному виду общего решения линейного однородного дифференциального уравнения (8.46) с постоянными коэффициентами.

Рассмотрим наиболее распространенный частный случай уравнения (8.46) – его аналог 2-го порядка:

Для данного уравнения характеристическое уравнение (8.50) принимает вид:

Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического уравнения рассматривают три случая, приведенных в таблице 8.1.

Пример 8.17. Найти общее решение уравнений:

а) Составляем характеристическое уравнение λ 2 +2 λ – 15 = 0. Корнями этого уравнения будут λ ₁ = –5 и λ ₂ = 3 . Тогда, применяя (8.53), получаем общее решение: y=C ₁ e – 5x +C ₂ e 3x .

б) Составляем характеристическое уравнение λ 2 – 16 λ + 64 = 0.

Решая это уравнение, получим λ ₁ = λ ₂ = 8 . Так как корни равные, то, применяя (8.54), будем иметь:

в) Характеристическое уравнение λ 2 – 4 λ + 13 = 0 имеет комплексные корни λ ₁ = 2+3 i и λ ₂ = 2 –3 i . Положив в (8.55) α=2 и β = 3, получим общее решение: .

г) Характеристическое уравнение λ 2 +9 = 0 имеет корни λ 1;2 = ± 3 i . П олагая в (8.55) α=0 и β = 3, получим общее решение

Рассмотрим теперь линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

Теорема 8.4. Пусть задано линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами и п равой частью специального вида

1. Если не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение уравнения (8.57) имеет вид:

где – многочлены общего вида (с неопределенными коэффициентами).

2. Если – корень характеристического уравнения кратности s , то частное решение уравнения (8.57) имеет вид:

– многочлены общего вида

Рассмотрим в таблице 8.2 некоторые случаи составления частного решения линейного неоднородного дифференциального уравнения (8.57) по специальному виду его правой части.

Пример 8.18. Найти общее решение уравнения .

Решение. Найдем общее решение соответствующего однородного ДУ: . Х арактеристическое уравнение λ 2 +2 λ +1 = 0 имеет корень λ₁ = 1 кратности 2 (смотри таблицу 8.1). Значит, y_{o . o .} = c ₁ ∙ e x + c ₂ ∙ x ∙ e x . Находим частное решение исходного уравнения. В нем правая часть x –4=( x –4)∙ e 0∙ x есть формула вида P ₁ ( x )∙ e 0∙ x , причем α= 0 не является корнем характеристического уравнения: α ≠ λ . Поэтому согласно формуле (8.58), частное решение y _ч.н. ищем в виде y _ч.н. = Q ₁ ( x )∙ e 0∙ x , т.е. y _ч.н. = Ax + B , где A и B – неопределенные коэффициенты. Тогда

Пример 8.19. Решить уравнение .

уравнения . Характеристическое уравнение λ 2 – 4 λ +13 = 0 имеет корни λ₁ = 2+3 i , λ 2 = 2 –3 i (смотри таблицу 8.1). Следовательно, .

Находим частное решение y _ч.н. . Правая часть неоднородного уравнения в нашем случае имеет вид

Отсюда, сравнивая коэффициенты при косинусе и синусе, имеем . Следовательно, A = 1, B = – 3 . Поэтому . И наконец, с учетом теоремы 8.3 получаем общее решение заданного линейного неоднородного ДУ в виде:

Пример 8.20. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение . Находим общее решение однородного уравнения . Характеристическое уравнение λ 2 – λ – 2 = 0 имеет два корня λ ₁ = –1 и λ ₂ = 2 (смотри таблицу 8.1) ; тогда y_{o . o .} = C ₁ ∙ e – x + C ₂ ∙ e 2 x – общее решение соответствующего однородного ДУ.

В правой части заданного уравнения имеется показательная функция. Так как в данном случае α=2 совпадает с одним из корней характеристического уравнения, то частное решение следует искать в виде функции Axe 2 x . Таким образом, y _ч.н. = Axe 2 x . Дифференцируя дважды это равенство, по лучим: . Подставим y _ч.н. и ее производные в левую часть заданного уравнения и найдем коэффициент A : . Следовательно, частное решение y _ч.н. = 3xe 2 x , общее решение

Используя начальные условия, определим значения произвольных постоянных C ₁ и C ₂ . Дифференцируя общее решение (8.60), получим:

Подставим в общее решение (8.60) значения x = 0 и y = 2, будем иметь 2 = C ₁ + C ₂ . Подставим в выражение для значения x = 0 и , будем иметь: 13 = – C 1 +2 C 2 +3 ; 10 = – C 1 + C 2 . Из этих уравнений составим систему , из которой находим: C 1 = – 2 и C 2 =4 . Таким образом, есть то частное решение, которое удовлетворяет заданным начальным условиям

Теорема 8.5 (о наложении решений). Если правая часть уравнения (8.56) представляет собой сумму двух функций: , а y _{1 ч.н.} и y _{2 ч.н.} – частные решения уравнений и соответственно, то функция

является частным решением данного уравнения