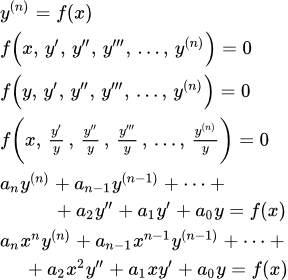Дифференциальное уравнение высшего порядка это

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021

Основные понятия и определения дифференциальных уравнений высших порядков

Дифференциальное уравнение n-го порядка имеет вид или, если оно разрешено относительно ,

Задача нахождения решения уравнения (I), удовлетворяющего начальным условиям

называется задачей Коши для уравнения (1).

Теорема существования и единственности решения задачи Коши . Если в уравнении (1) функция

а) непрерывна по всем своим аргументам в некоторой области их изменения,

б) имеет ограниченные в области частные производные по аргументам , то найдется интервал , на котором существует единственное решение уравнения (1), удовлетворяющее условиям

где значения содержатся в области .

Для уравнения второго порядка начальные условия имеют вид

где — данные числа. В этом случае теорема существования и единственности геометрически означает, что через данную точку плоскости с данным тангенсом угла наклона касательной проходит единственная кривая.

Рассмотрим, например, уравнение и начальные условия

В данном случае . Эта функция определена и непрерывна при всех значениях . Ее частные производные по и равны соответственно

и являются всюду непрерывными и ограниченными функциями своих аргументов. Следовательно, каковы бы ни были начальные условия

существует единственное решение данного уравнения, удовлетворяющее этим условиям.

Общим решением дифференциального уравнения n-го порядка (1) называется множество всех его решений, определяемое формулой , содержащей произвольных постоянных таких, что если заданы начальные условия (2), то найдутся такие значения , что будет являться решением уравнения (1), удовлетворяющим этим начальным условиям.

Любое решение, получаемое из общего решения при конкретных значениях произвольных постоянных называется частным решением дифференциального уравнения (1).

Уравнение вида , которое определяет неявно общее решение дифференциального уравнения, называется общим интегралом уравнения . Давая постоянным , конкретные допустимые числовые значения, получим частный интеграл дифференциального уравнения. График частного решения или частного интеграла называется интегральной кривой данного дифференциального уравнения.

Пример 1. Показать, что есть общее решение дифференциального уравнения .

Решение. Покажем, что удовлетворяет данному уравнению при любых значениях постоянных и . В самом деле, имеем .

Пусть теперь заданные произвольные начальные условия . Покажем, что постоянные и можно подобрать так, что будет удовлетворять этим условиям. Имеем . Полагая , получаем систему

из которой однозначно определяются и . Таким образом, решение удовлетворяет поставленным начальным условиям.

Геометрически это означает, что через каждую точку плоскости с заданным угловым коэффициентом проходит единственная прямая.

Задание одного начального условия, например , определяет пучок прямых с центром в точке , т.е. одного начального условия недостаточно для выделения единственного решения.

Дифференциальные уравнения высших порядков: ЛОДУ, примеры решения.

Можно выделить 5 возможных метода для определения y₀ — общего решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами:

1. В случае, когда все решения характеристического уравнения являются действительными и различными, значит, линейно независимые частные решения принимают вид:

,

а общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами записывают так:

.

Найти общее решение ЛОДУ 3-го порядка с постоянными коэффициентами:

.

Для начала записываем характеристическое уравнение и находим его корни, перед этим произведя разложение многочлена в левой части равенства на множители методом группировки:

Каждый из трех корней характеристического уравнения являются действительными и различными, значит, общее решение линейного однородного дифференциального уравнения 3-го порядка с постоянными коэффициентами принимает вид:

.

2. Когда каждое решение характеристического уравнения оказывается действительными и одинаковыми, т.е.,

,

значит, линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами принимают вид:

,

а общее решение линейного однородного дифференциального уравнения (ДУ) принимает вид:

Найти общее решение ДУ

.

Характеристическое уравнение этого линейного однородного дифференциального уравнения 4-го порядка выглядит так:

.

Обратившись к формуле бинома Ньютона, переписываем характеристическое уравнение как , из чего видим четырехкратный корень k₀ = 2.

Т.о., общим решением заданного ЛОДУ с постоянными коэффициентами является:

.

3. Когда решениями характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами оказываются разные комплексно сопряженные пары , n=2m, тогда линейно независимые частные решения такого линейного однородного дифференциального уравнения принимает вид:

а общее решение записывается так:

Проинтегрировать ЛОДУ 4-го порядка с постоянными коэффициентами .

Характеристическое уравнение этого линейного однородного дифференциального уравнения:

.

Произведя некоторые несложные преобразования и группирования имеем:

Откуда находим 2 пары комплексно сопряженных корней характеристического уравнения и . Тогда, общим решением заданного ЛОДУ n-ого порядка с постоянными коэффициентами является:

4. Когда решениями характеристического уравнения оказываются совпадающие комплексно сопряженные пары , тогда линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами выглядят так:

,

а общим решением этого линейного однородного дифференциального уравнения является:

Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами:

.

Первым шагом записываем характеристическое уравнение этого ЛОДУ с постоянными коэффициентами и определяем его корни:

Т.е., решением характеристического уравнения является двукратная комплексно сопряженная пара . Тогда общее решение заданного ЛОДУ с постоянными коэффициентами будет:

.

5. Могут возникнуть любые комбинации случаев, описанных выше, т.е., некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые являются действительными и совпадающими, некоторые являются различными комплексно сопряженными парами и некоторые совпадающими комплексно сопряженными парами.

Найти общее решение ДУ

.

Характеристическое уравнение этого ЛОДУ с постоянными коэффициентами выглядит так:

.

Многочлен в левой части равенства можно разложить на множители. Из делителей свободного члена вычисляем двукратный корень k₁=k₂=2 и корень k₃=-3. Далее, применяя схему Горнера, приходим к разложению:

.

Из квадратного уравнения находим оставшиеся корни .

Т.о., общее решение заданного ЛОДУ с постоянными коэффициентами выглядит как:

.