Дифференциальное уравнения прогиба оси изогнутой балки

Дифференциальное уравнение оси изогнутой балки

Для определения уравнения оси изогнутой балки воспользуемся законом Гука:

.

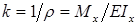
Выражение для кривизны некоторой кривой:

.

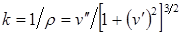
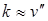
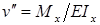
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки ( уравнение изгиба ) в рассматриваемом месте балки:.

Продифференцировав полученное уравнение дважды по z, получим дифференциальное уравнение оси изогнутой балки : .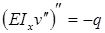

Интегрирование дифференциального уравнения оси изогнутой балки

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки.

Изогнутая ось балки

Изогнутая ось балки

Изгиб балки сопровождается искривлением ее оси. При этом точки оси получают поперечные перемещения или прогибы, а поперечные сечения поворачиваются относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона j касательной к изогнутой оси балки. Прогибы и углы поворота в балках часто называются линейными и угловыми перемещениями.

— закон изменения прогиба оси балки;

АМВ – изогнутая ось (упругая линия) – кривая, в которую превращается прямолинейная до деформации ось балки после приложения нагрузки;

— угол наклона касательной.

Прогибы и углы поворота в балках являются переменными величинами, т. е. функциями координаты х.

О знаке :

j — положительно, если при совмещении оси балки с касательной идет движение по часовой стрелке.

На часть конструкций часто накладываются жесткие ограничения на перемещения, например для балочных мостов, кран-балок и т. д., т. е. возникает необходимость рассмотрения геометрической стороны задачи при изгибе.

I . Дифференциальное уравнение изогнутой оси балки

Вид ИОБ определяется

1. действием нагрузки, которая вызывает внутренние усилия M , Q , N ;

2. геометрической характеристикой I ;

Значит

I – момент инерции поперечного сечения балки относительно его нейтральной оси;

Е – модуль упругости материала балки.

, E , I – от x не зависят.

В лекции «Напряжения в случае плоского поперечного изгиба балки» (прошлый семестр) рассматривалось «Определение нормальных напряжений». При этом было рассмотрено 3 стороны задачи:

1. геометрическая сторона задачи;

2. физическая сторона задачи;

3. статическая сторона задачи.

При рассмотрении геометрической стороны задачи была установлена зависимость

, где

— относительная деформация;

— прогиб оси балки;

— радиус кривизны ИОБ.

При рассмотрении физической стороны задачи была использована гипотеза о том, что продольные волокна балки не давят друг на друга, т. е. что изгиб сводится к деформациям продольных волокон, которые деформируются изолированно, испытывая простое одноосное растяжение (сжатие). Эта гипотеза делает возможным для связи деформаций и напряжений при изгибе использование закона Гука.

В статической стороне задачи было рассмотрено следующее сечение

Суммарное действие внутренних напряжений должно быть равно внешним воздействиям.

Имеет место 2 условия равновесия:

1.

2.

— сила по элементарным площадкам;

— сила по всему сечению.

Отсюда (1),

— радиус кривизны ИОБ;

— жесткость балки при изгибе (изгибная жесткость).

Так как в выражение (1) вошли все 3 фактора M , E , I , то осталось выразить через y .

Для этого воспользуемся выражением из высшей математики

(2)

Приравниваем (1) и (2).

(3) точное дифференц. уравнение ИОБ

Так как в реальных конструкциях нормами проектирования допускаются сравнительно малые прогибы, а именно

, то ИОБ в реальности пологая.

Угол

Поскольку , а , то этим слагаемым в выражении (3) можно пренебречь.

(4)

Эта формула устанавливает зависимость между ,и 2-ой производной от прогиба.

Известно, что , когда момент, растягивая нижние волокна, обращает балку выпуклостью вниз.

Тогда из математики (вторая производная от функции отрицательна, если кривая обращена выпуклостью в положительную сторону оси y ).

Таким образом, при положительном изгибающем моменте, 2-ая производная должна быть отрицательной, следовательно в уравнении (4) удерживается знак «-» и формула имеет вид

(5) приближенное дифференц. уравнение ИОБ

Основные дифференциальные зависимости

Ранее известные зависимости:

(6)

,

(7)

Уравнения (7) позволяют, имея q , Q и M (а эти величины всегда возможно определить, построив эпюры в балках), получить значения y (прогиба) и j (угла поворота).

II . Методы решения дифференциальных уравнений ИОБ

Существует 3 метода решения дифференциальных уравнений ИОБ:

1. Метод непосредственного интегрирования

2. Метод начальных параметров

1. Метод непосредственного интегрирования

Метод непосредственного интегрирования заключается в непосредственном интегрировании уравнения (5).

(8)

Зная закон изменения можно определить y как функцию от x ().

Интегрирование ведется по участкам, для которых должны быть известны аналитические выражения изгибающих моментов .

В результате двукратного интегрирования на каждом участке появляются 2 произвольные постоянные С1 и С2.

Если балка разбивается на n участков, то постоянных интегрирования будет 2 × n .

Их определяют из

1. граничных условий (способов закрепления);

2. условий сопряжения участков.

1. Условия закрепления (граничные условия)

1) жесткое защемление

При Þ и

2) шарнирное опирание

При Þ и

При Þ и

Таким образом, с учетом граничных условий осталось неизвестных.

2. Условия сопряжения граничных участков

при Þ ,

Таким образом, всегда можно составить условия сопряжения и найти уравнение ИОБ.

Дифференциальное уравнение изогнутой оси. В большинстве случаев практического расчета деталей, работающих на изгиб, необходимо также производить расчет их на жесткость

Дифференциальное уравнение изогнутой оси

• Дифференциальные уравнения криволинейной оси В предыдущем пункте мы рассмотрели вопросы, связанные с расчетом прочности балок. В большинстве случаев при практическом расчете детали, работающей на изгиб, также необходимо рассчитать ее жесткость. Под расчетом жесткости мы понимаем оценку упругой гибкости балки под действием 269 выбор размеров сечения таким образом, чтобы применимая нагрузка и движение не превышали пределов,

установленных нормами. Чтобы произвести такие расчеты, нужно научиться рассчитывать смещение точек балки под действием внешних нагрузок. Этот навык также необходим для расчета статически неопределимых балок. Рассмотрим деформацию балки с плоским изгибом. Ось балки(рис. 272) под действием нагрузки, расположенной на одной из главных плоскостей инерции (в плоскости Хоу), изгибается в ней Одна и та же плоскость и поперечное сечение вращаются и одновременно получают

посто в движении тела. Изогнутая ось луча называется изогнутой осью или Людмила Фирмаль

упругой линией. Для риса. Криволинейные оси 272 и 273 представлены тонкими кривыми. Движение центра тяжести сечения в направлении, перпендикулярном оси балки, называется отклонением балки в этом сечении и w. Fig. it обозначается буквой «в». 272 и 273 центр тяжести любого сечения, взятый на расстоянии x от начала координат, перемещается вертикально от точки 0g до точки 02PA на расстоянии 0t02. Это смещение является отклонением луча w (x) в поперечном сечении абсциссы. Угол, на который каждая секция поворачивается относительно своего

первоначального положения, 0, называется углом поворота секции. Угол поворота можно также определить как угол между касательной упругой линии и осью х(рис. 273). Заметим, что длина кривой оси, принадлежащей нейтральному слою, поскольку она не изменяется по кривизне луча, смещение точки также происходит в направлении оси Х (перемещение 0103 на фиг. 274). Однако в большинстве случаев смещение V (проекция полного смещения на ось x)пренебрежимо мало. Координатные оси всегда могут быть расположены следующим образом: начало координат расположено на левом краю балки, ось x-непосредственно вдоль оси балки вправо, а ось w вверх. Если

• движение соответствующей точки происходит вверх, то есть в направлении оси W, то отклонение w считается положительным. 270 угол поворота при повороте сечения против часовой стрелки считается положительным. Из-за малой деформации балки можно предположить tg0″0. Так как тангенс угла поворота является производной от координат отклонения: (10.39) Тогда с достаточной точностью угол поворота этого сечения 0 (x) равен производной прогиба w (x) по абсциссе сечения: (Да. Сорок) Поэтому для определения деформации балки в ее произвольном поперечном сечении необходимо, прежде всего, получить уравнение упругой

линии w=F (x). Рис двести семьдесят пять М Н>м>0х Исходя из физических свойств изогнутой оси балки, можно сказать, что упругая линия должна быть непрерывной и гладкой (без разрыва) кривой, создавая тем самым гладкую линию. Угол отклонения и поворота-это перемещение поперечного сечения балки в изгибе. Деформация поперечного сечения балки определяется кривизной ее изогнутой оси, то есть кривизной. Поскольку влияние поперечной силы на кривизну невелико, то в общем случае уравнения поперечного изгиба (10.9) 1 м(x) p(x) можно записать как»EJ (x)«. (10.41) Из курса высшей математики нам известно уравнение

кривизны плоской кривой: (ПВ (10.42) Теперь, чтобы получить дифференциальное уравнение криволинейной оси, остается Людмила Фирмаль

приравнять правильную часть выражений (10.41) и (10.42), в которых впервые раскрыта задача о знаке. Если изгибающий момент положительный, то упругая линия обращена вогнутой стороной вверх(рис. Поэтому в предполагаемом направлении осей координат кривизна k=—считается положительной. При отрицательном изгибающем моменте кривизна также отрицательна(рис. 275, б). Ось W 271) вниз, а кривизна отрицательна для положительных изгибающих моментов(рис. 275, В), а в отрицательные моменты-положительные(рис. 275, г), сохраняя направление оси сверху, имея соответствие между знаком момента и знаком кривизны, так что положительная часть уравнения (10.41) и (10.42) являются единичными, а затем d2w (10.43) Если ось W расположена*вниз,

то знак минус должен располагаться справа. В результате получается уравнение: 曲線の軸の正確な方程式と呼ばれますbeam. It это нелинейное дифференциальное уравнение второго порядка, интегралы которого, как известно, представляют значительные трудности. В связи с этим и в большинстве рассмотренных на практике задач прогиб невелик, поэтому точное уравнение (10.43) заменяется приближенной формулой, представляющей собой уравнение малых перемещений. Знаменатель выражения (10.43) представляет собой сумму двух членов: При малых деформациях значение второго члена во много раз меньше первого. Дело в том, что при расчете обычного инженерного или строительного элемента норма допустимого

отклонения составляет 1/100-1/1000 пролетного строения, в зависимости от условий работы балки, а полученный угол поворота зависит от степени отклонения балки. Даже если мы примем больший предел отклонения[f= — максимальное значение тангенса 0, мы будем выглядеть так: tg0 «=tg1° » 0.02. Таким образом, значение tg2 0 не превышает 0,0004, то есть оно очень мало по сравнению с единицей. Эти значения больше не могут быть проигнорированы и имеют ошибку. Тогда мы получим упрощенное дифференциальное уравнение упругих линий: d2w м (х) DX * Эдж (к) 9 (10.44) Изгибающий момент M (X) рассчитывается для недеформированной балки.

В дальнейшем уравнение(10.44) называют основным дифференциальным уравнением упругой линии (для малых деформаций). С его помощью можно рассчитать перемещение балки при любых условиях нагрузки. Решая задачу аналитическим методом, углы поворота 0 (l) и отклонения w (x) вычисляются путем последовательного интегрирования ОС- 172w (х)=ДХ Джей Джей Четыре. Новое дифференциальное уравнение (10.44). Если мы интегрируем уравнение впервые, то получим уравнение угла поворота 0 (x): (Значения i0. 4S) Значения w L-d x+C x+D, (10.46) константы C и D, содержащие две произвольные константы C и D, определяются из условия фиксации балки следующим образом:

а)балка имеет уплотнение на конце 276), тогда прогиб и угол поворота в ней равны нулю: u>e=0;vy=0;(10.47) Б)для балки на двух шарнирных опорах(рис. 273) равен нулю прогиб этих опор: wA=0; wb=Q-(10.48) заметим, что заданные моменты не являются M (x), а учитывая нагрузку q (x), уравнение упругой линии иногда удобно записать в другом виде. Помните, что it=H ( * ), а дифференциальное уравнение (10.44) дважды, мы получаем rf* ДХ международный (ПВ (х)](. Z3J вопрос(10.49) Формула для упругой линии вида (10.49) применяется с учетом расчета балки на упругом основании и изменения балки.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института