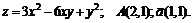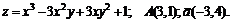Тема 2. дифференциальные уравнения
Геофильтрации и геомиграции
Теоретическая часть
Емкостные свойства горных пород
При рассмотрении системы вода — порода важное значение имеют так называемые емкостные свойства пород. Под емкостными свойствами понимают способность горных пород вмещать, удерживать и отдавать заключенную в них ПВ. Емкостные свойства определяют общие запасы ПВ, содержащиеся в водоносном горизонте. Процессы отдачи ПВ (водоотдачи) горными породами подразделяются на гравитационные и упругие.
Гравитационная емкость определяется как отношение объема свободной гравитационной воды, содержащейся в образце (элементе) горной породы при полном насыщении, к объему образца.
Гравитационная емкость, определяемая при осушении горной породы, называется водоотдачей (м) и может быть рассчитана как разностьмежду полной и наименьшей влагоемкостью, т.е.

при насыщении горной породы она называется недостатком насыщения, равным разности между полной влагоемкостью и естественной влажностью данного грунта, т.е.

Напомним, что под полной влагоемкостью (Wo)понимают максимально возможное количество воды (все виды воды) при полном заполнении свободного пространства в минеральном скелете горной породы, а под наименьшей влагоемкостью (водоудерживающая способность горной породы) (Wн) понимают влажность, определяемая максимальным количеством прочносвязанной, осмотической, капиллярно-разобщенной и капиллярно-подвешенной воды.
Таким образом, величина водоотдачи зависит от свойств самой горной породы (общая пустотность, размеры пустот, структура «свободного» пространства, минеральный состав и др.), определяющих суммарное количество различных видов связанной воды (Wн) и объем воды при полном насыщении (Wo), и в этом смысле может рассматриваться как объективное свойство (параметр) данной породы. В определенной мере водоотдача зависит также от скорости осушения горной породы (скорости снижения уровня полного насыщения), поскольку эта скорость может определять (при прочих равных условиях) формирование различных объемов капиллярной воды (капиллярно-подвешенная вода).
Величина недостатка насыщения ( 
В заключении рассмотрения фильтрационных и емкостных параметров горных пород приведем классификацию горных пород по проницаемости (табл.2.1).
Под упругой водоотдачейпонимается способность горной породы отдавать заключенную в них ПВ за счет упругого расширения жидкости и упругого сжатия горной породы. Количественно упругая водоотдача характеризуется коэффициентами упругоемкости пласта и упругой водоотдачи.
Запишем теперь выражение для относительного изменения объема воды V0 в рассматриваемом объеме породы Vп, имея в виду, что V0 = n Vп:



где 
Классификация горных пород по проницаемости
| Группа пород | Проницаемость (Кф, м/сут) | Гравитационная емкость (водоотдача), m | Типы горных пород |
| Очень высокопроницаемые | более 100 | 0.2 — 0.3 0.1 — 0.15 | Гравийно-галечниковые образования, интенсивно закарстованные породы (известняки, гипсы) |
| Хорошо (высоко) проницаемые | 10-100 | 0.2 — 0.25 0.1 — 0.15 | Крупнозернистые и грубозернистые пески, интенсивно трещиноватые скальные породы (песчаники, граниты, базальты ) |
| Проницаемые | 0.1 — 10 | 0.15 — 0.2 0.05 — 0.1 | Разнозернистые, тонко- и мелкозернистые глинистые пески, слаботрещиноватые и закарстованные горные породы |
| Слабопроницаемые | 10 -6 — 10 -2 | 0.01 — 0.03 | Суглинки, глины песчанистые или микротрещиноватые, очень слаботрещиноватые скальные породы, незакарсто- ванные известняки |
| Практически непроницаемые | меньше 10 -6 | менее 0.01 | Плотные нетрещиноватые глины, практически нетрещиноватые скальные породы |
Численно он равен


где g0 — объемная масса жидкости; е — коэффициент пористости, е = n/(1-n); Eв= модуль Юнга для воды (для чистой воды Ев= 2 
Коэффициент упругоемкости 
В отличие от коэффициента упругоемкости коэффициент упругой водоотдачи является величиной безразмерной и характеризует объем жидкости, получаемой с единицы площади водоносного горизонта при снижении напоров на 1 метр.
Значения коэффициент упругоемкости для различных типов пород
| Порода | Коэффициент упругоемкости  (м -1 ) (м -1 ) |
| Пески | (0.5  5) 5)  10-4 10-4 |
| Супеси и суглинки | 10-4-10-3 |
| Трещиноватые породы | 10-5-10-6 |
Коэффициент упругой водоотдачи 



где m — мощность водоносного горизонта, т.к. в соответствии с таблицей значения 


Для однородного изотропного пласта



a* = 
Уравнение вида (2.8), называется уравнением Фурье и широко исследовано в теории теплопроводности.
Таким образом, в отличии от жесткого режима движения в напорном пласте, уравнения упругого режима напорной фильтрации содержат производную по времени, т.е. в этом случае Н=Н (x, y, z, t), и движение является нестационарным. Физически это означает, что по мере уменьшения напоров во времени в водоносном пласте постепенно срабатываются его упругие запасы. Высвобождающиеся при этом объемы воды «вносятся» в общий баланс фильтрационного потока в водоносном пласте. Реакция от возмущения напоров на границе или в какой-либо области рассматриваемого пласта распространяется от границы (области) по пласту постепенно, причем скорость распространения тем больше, чем выше проницаемость и чем меньше упругоемкость горной породы. Следовательно, отношение a* = 


Плановая фильтрация в изолированном напорном пласте
Уравнение напорной фильтрации для жесткого режима:

где Tx = kxm и Ty = kym — коэффициенты водопроводимости пласта в направлениях осей x и y (совпадающих в общем случае с направлением главных осей анизотропии).
При Tx = Ty = T = const получаем:

В упругом режиме имеем


где m* = m 
Для однородного изотропного пласта постоянной мощности:



где а* — коэффициент пьезопроводности, который в данном случае может быть выражен в виде:
Плановая напорная фильтрация при наличии перетекания
Рассмотрим схему на рис., где изображены два напорных пласта с напорами Н и Н’ соответственно. Выводя уравнение неразрывности для элементарного столбика в пределах нижнего пласта, мы должны учесть поступление воды не только через боковые грани столбика (как в случае изолированного пласта), но и через его верхнюю грань: здесь проходит вода, перетекающая из верхнего пласта через разделяющий относительный водоупор.
Рис.2.1 Схема к выводу уравнения неразрывности в пласте с перетеканием
При расчетах подобных водоносных систем принимаются следующие предположения, известные как предпосылки перетекания (предпосылки Мятиева-Гиринского):
1) движение в водоносных пластах является плановым (линии тока параллельны напластованию);
2) в разделяющем слое линии тока перпендикулярны к напластованию; физически эта предпосылка вполне объяснима: вода стремится пройти участок с большим сопротивлением (водоупорный слой) по кратчайшему пути.
Принимая теперь вторую предпосылку перетекания, т.е. считая, что длина пути фильтрации по слабопроницаемому слою равна mp, получаем, что градиент фильтрации здесь равен:
Ip = 
Замечание. Одновременно мы тем самым предположили, что режим фильтрации в разделяющем слое является жестким, т.е. в этом слое мгновенно устанавливается распределение напоров в соответствии с напорами на его кровли Н’ и подошве Н. Иначе говоря, мы пренебрегли упругими запасами воды в разделяющем слое.
Следовательно, через верхнюю грань столбика поступает дополнительное питание, равное
eп = kp
на единицу площади пласта в единицу времени; величина eп входит в качестве дополнительного члена в уравнение неразрывности, так что вместо (41) получаем:


Соответственно преобразуются и дифференциальные уравнения фильтрации. Так, вместо результирующего уравнения (2.13) получаем




где B = 
Конвективный перенос в подземных водах
Конвективный перенос можно определить как механический (гидравлический) перенос фильтрационным потоком (статистически усредненным в только что упомянутом смысле) без отделения от него, т.е. при этом считается, что вещество или тепло перемещается со средней действительной скоростью Vд связанной со скоростью фильтрации соотношением (2.16).
Vд = 

где na – так называемая активная пористость (трещиноватость).
Вместе с тем величина na, является весьма условным параметром. При больших скоростях и малом времени перенос идет по наиболее крупным, связанным друг с другом порам. С падением скорости и увеличением времени в процесс вовлекаются более мелкие и “тупиковые” поры, так что впределе активная пористость (трещиноватость) стремится к общей пористости (трещиноватости). За исключением специально оговоренных случаев, мы будем далее предполагать, что рассматриваются достаточно длительные и медленные процессы, вкоторых величину naможно считать постоянной, близкой к общей пористости (трещиноватости)’. Соответственно, мы примем для нее далее обозначение n.
Конвективный перенос должен характеризоваться резкой границей раздела между вытесняющей и вытесняемой жидкостью, т. е. перемешивания нет, и говорят о поршневом вытеснении одной жидкости другою. При плановой фильтрации в однородном пласте двух жидкостей с одинаковой плотностью фронт вытеснения нормален к поверхностям напластования (рис., А). Ситуация, однако, заметно усложняется, если плотности жидкостей различны: фронт вытеснения, в частности, отклоняется от нормали к напластованию — более тяжелая жидкость занимает вблизи фронта нижнюю часть пласта (рис., Б).
Конвективный перенос сорбируемого вещества
Конвективный перенос сопровождается процессами физико-химического взаимодействия переносимых компонентов с вмещающими породами – сорбцией, десорбцией, растворением, ионным обменом и др. Наиболее распространенными и изученными являются процессы сорбции, во многом определяющие самоочищающую способность водоносных комплексов при миграции загрязнений.
При достаточно длительном взаимодействии раствора и породы зависимость между концентрацией компонента в растворе c и на твердой фазе N оказывается для данной температуры однозначной
где N0 — сорбционная емкость, определяющая предельно возможное в данных условиях содержание компонента в единице объема породы.
Для мало концентрированных растворов достаточно характерна линейная изотерма Генри:
где безразмерная константа kг определяющая отношение концентраций No и c, называется коэффициентом распределения для данной пары “раствор – порода”. Для несорбируемых компонентов kг = 0, а для хорошо сорбируемых – величина kгизмеряется сотнями и даже тысячами относительных единиц.
С другой стороны, ясно, что сорбция протекает во времени. Полная сорбционная емкость породы реализуется не сразу. Количество сорбируемого компонента, усвоенного единицей объема горной породы N(c, t), достигает своего предельного значения N0 (с) только после достаточно длительного соприкосновения минеральных зерен с внутрипоровым раствором, имеющим концентрацию с. Это обстоятельство приближенно отражается уравнением кинетики сорбции, связывающим линейно интенсивность сорбции с отклонением от равновесной концентрации:


где с – текущая средняя концентрация порового раствора; cc ( N ) – концентрация раствора непосредственно на контакте с поверхностью минерального скелета (связанная с текущей величиной N(t) (2.17); 
На практике время заметного проявления кинетики сорбции редко превышает несколько суток, а чаще измеряется часами. Поэтому в натурных условиях, когда длительность переноса измеряется месяцами и годами, внутрипоровой кинетикой сорбции обычно можно пренебречь,т. е. считать, что сорбция протекает мгновенно (это, конечно, не означает, что мгновенно исчерпывается и сорбционная способность породы!).
Рассмотрим в таком варианте процесс поршневого вытеснения впределах фиксированной трубки тока (фильтрационный поток – стационарный с расходом Q) . Взаимодействующие жидкости считаем однокомпонентными, так что количество солей однозначно характеризуется концентрацией: для вытесняемой (пресной) воды она равна с 0 , для вытесняющей (соленой) – с0. На фронте вытеснения имеет место сорбция, протекающая мгновенно. Составим баланс соли для элемента трубки (рис.) длиной dl, отвечающей перемещению фронта вытеснения за время dt.
Количество соли, поступившей слева, равно с0 Q dt, а поток соли вправо равен с 0 Q dt. Накопление соли в поровом пространстве элемента dlравно (с0 – с 0 ) n w dl(w – усредненное поперечное сечение трубки), а накопление соли на минеральном скелете за счет сорбции, согласно зависимости (2.17), равно (kгc0– kгc 0 ) w dl. Уравнение баланса имеет вид,
( c0 — c 0 ) Q dt = (с0 – с 0 ) n w dl + kг (c0–c 0 ) w dl. (2.20)

где vп – скорость перемещения фронта вытеснения. При отсутствии сорбции vп = vд, где средняя действительная скорость движения жидкости vдопределяется формулой (2.16).
Таким образом, сорбция, увеличивая емкость водоносной системы по отношению к соли, замедляет перенос. Скорость его в условиях сорбции vп, можно определить по формуле (2.16), подставляя в нее вместо активной пористости nтак называемую эффективную пористость:
которая формально выражает общую емкость водоносных пород по отношению к рассматриваемому сорбируемому компоненту. Подчеркнем, что при больших kг величина n э>>1.
Диффузионно — дисперсионные процессы.
Молекулярная диффузия и гидродисперсия
При наличии градиента концентрации возникает самопроизвольный перенос вещества под действием молекулярных сил. Общий поток вещества Qc в направлении Lчерез расчетное сечение wl при этом ориентирован в сторону уменьшения концентрации с и определяется законом Фика:


где Dм– коэффициент молекулярной диффузии в пористой среде, зависящий от ее структурных особенностей и физических свойств поровых растворов (его характерные значения для песчано-глинистых пород имеют порядок 10 -5 м 2 /сут).
Для сорбируемых компонентов величина Dм, соответственно, убывает. Скорость чисто молекулярного диффузионного переноса, как правило, мала, и учитывать ее следует только при малых скоростях фильтрации, в первую очередь – при оценке массопереноса через слабопроницаемые породы – разделяющие слои, экранирующие отложения хранилищ промышленных стоков, пористые блоки трещиноватых пород и т.п. Молекулярная диффузия проявляется при фильтрации воды как фактор рассеянии, действующий между жидкостями с различной концентрацией на фронте вытеснения.
В конечном счете внешним проявлением диффузии во всех случаях оказывается «размыв» границы между вытесняемой и вытесняющей жидкостями, образование вблизи фронта вытеснения переходной зоны Lп пределах которой концентрация вещества изменяется постепенно от с0до с 0 (рис.), в отличие от резкой границы, характерной для чисто конвективного переноса (т.е. для схемы поршневого вытеснения). По такому внешнему проявлению с молекулярной диффузией ассоциируется еще один механизм переноса вещества – механическая дисперсия.
Однако природа этого явления существенно иная: механическая дисперсия обусловлена неоднородностью поля действительных скоростей. Если, например, все окрашенные частицы воды на (рис) начинают одновременно двигаться в фильтрационном потоке, имеющем среднюю действительную скорость vд, от поперечного сечения АА в направлении ВВ, то за время t=L/vд одни из этих частиц пройдут путь существенно больший, чем L, а другие – меньший. В результате вместо резкого контакта окрашенной и неокрашенной жидкости, характерного для начального момента (сечение АА), вблизи сечения ВВэтот контакт окажется размытым – вследствие рассеяния окрашенных частиц фильтрационным потоком. Согласно экспериментам, подобное рассеяние, называемое фильтрационной диффузией, или механической дисперсией, также подчиняется закону Фика (2.23), однако при замене коэффициента молекулярной диффузии Dм на другой параметр – коэффициент механической дисперсии Dд.
Как показывают эксперименты, при достаточно больших скоростях фильтрации v в однородных грунтах величина Dд оказывается примерно пропорциональной скорости фильтрации v:
Dд = 
где константа 
Для однородных песков параметр 

В результате при больших скоростях потока величина Dд может на несколько порядков превосходить характерные значения коэффициента молекулярной диффузии.
Аналогия в характере проявления молекулярной диффузии и механической дисперсии способствовала их объединению через суммарный коэффициент:
D = Dм + Dд = Dм + 
который далее для краткости будет именоваться коэффициентом дисперсии.
Соответственно, суммарное рассеяние вещества, вызываемое гидродисперсией, или просто дисперсией, определяется законом Фика в виде:


Феноменологическая закономерность (2.26) является, таким образом, некоторым усредненным детерминированным отражением процесса, имеющего на самом деле ярко выраженный вероятностный характер. Благодаря подобным усреднениям, мы отказываемся от стохастического анализа процессов массопереноса на микроуровне, связанного с необходимостью использования статистической теории фильтрации. Важно отметить, что дисперсия может идти не только вдоль направления фильтрационного потока (как мы до сих пор предполагали), но и в перпендикулярном к нему направлении. Такая – поперечная – дисперсия также подчиняется закону вида (2.26), но с иным коэффициентом D’, имеющим, подобно (2.25), вид:
геометрический параметр 
Значение поперечной дисперсии проще всего проиллюстрировать, запуская меченые частицы жидкости не по всей ширине, а лишь на ограниченном участке фильтрационного потока. Поперечная дисперсия приводит к распространению меченых частиц за пределами зоны, ограниченной крайними траекториями фильтрации меченой жидкости, к появлению здесь переходных зон и к уменьшению скоростей продвижения фронта вытеснения в продольном направлении. Все это хорошо иллюстрируется (рис.), полученным по конкретному эксперименту. Слагаемые в формулах (2.25, 2.27) отражают интенсивность молекулярно-диффузионного и механического дисперсионного массопереноса: доля каждого из них в общем балансе массового потока определяется скоростью фильтрации v и структурой горных пород ( для однородных пород — характерным размером минеральных зерен dз).Так, из результатов лабораторных экспериментов следует, что при vdз, порядка 0,0001 м 2 /сут и менее доминирующей является молекулярная диффузия, а при параметре vdз измеряемом сотыми – десятыми долями квадратных метров в сутки, резко преобладает уже механическая. Поэтому, с определенной долью погрешности, можно говорить, что в породах глинистого состава обычно можно учитывать только молекулярную диффузию, в трещиноватых породах — только механическую дисперсию, но в остальных случаях это требует дополнительного обоснования.
Конвективно-дисперсионный перенос в однородных водоносных пластах
При выводе фундаментального решения задачи конвективно-дисперсионного переноса в однородных водоносных пластах мы ограничимся рассмотрением жидкостей с постоянной плотностью (и вязкостью). Это позволяет значительно упростить анализ миграционных процессов: «фильтрационная часть» задачи может решаться заранее, отдельно,– независимо от задачи переноса; поэтому фильтрационное поле считается нами заданным.
Рассмотрим совместное проявление конвекции и дисперсии в однородном пласте, сложенном гомогенными водоносными породами – пористыми или «чисто» трещиноватыми (рис.а). Фильтрационный поток считаем одномерным (плоскопараллельным) и стационарным. Исходная концентрация вещества повсеместно равна c 0 . В момент t = 0концентрация на левой границе принимает постоянное значение c0 и соленые воды начинают перемещаться по пласту в направлении оси X. Поток соли qcчерез произвольное сечение пласта обусловлен конвекцией ( 


qс = 


Составим уравнение неразрывности для элемента dx:
qc dt — [ qc — 

где справа записано приращение количества соли в элементе dx(с объемом порового пространства, равным nmdx, причем при наличии сорбции величина nзаменяется на nэсогласно (2.22) за время dt, а слева – разность между количеством соли, поступившей в этот элемент и вытекшей из него за то же время dt. Подставляя сюда выражение (2.28) для qc приходим к дифференциальному уравнению конвективно-дисперснонного переноса относительно неизвестной концентрации c(х, t)
n 


Начальные и граничные условия имеют вид:

Последнее граничное условие отражает отсутствие гидродисперсионного переноса в зоне с постоянной (исходной) концентрацией c 0 . Введем относительную концентрацию

и получим окончательную математическую формулировку фундаментальной задачи ми грации:
n 



Решение этой задачи, формально напоминающей фундаментальную задачу фильтрации , можно представить в виде









а erfc(z) – табличная функция.
При достаточно больших q вторым членом в правой части (2.34) можно пренебречь, внося при этом погрешность е порядка: e=0,3/ 


Графическое представление решения (2.35) дается на (рис б). На графике выделяются три зоны: I – зона вытесняющего раствора, III – зона вытесняемого раствора и II – переходная зона ‘, в пределах которой относительная концентрация меняется от значений, близких к 1, до значений, близких к 0.
На рисунке пунктиром показан также график изменения концентрации при поршневом вытеснении, когда дисперсия отсутствует (D = 0). Понятно, что точка xп, согласно (2.16), отвечает условию:
xп =
и, следовательно, в случае, описываемом решением (2.35),


т. е. точка xп располагается посредине переходной зоны. Физически это вполне понятно: на фоне продвижения фронта поршневого вытеснения, отвечающего конвекции, развивается дисперсия, приводящая к размыванию фронта, симметричному относительно его расчетного положения xп.
Ориентировочно можно полагать, что дисперсией допустимо пренебречь при
Дифференциальные уравнения
Высшего образования
«Сибирский федеральный университет»
ИНСТИТУТ ГОРНОГО ДЕЛА, ГЕОЛОГИИ И ГЕОТЕХНОЛОГИЙ
МАТЕМАТИКА
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников специальностей
Горное дело»
Горные машины и оборудование
Электрификация и автоматизация горного производства
Открытые горные работы
Семестра
Федеральное государственное автономное
образовательное учреждение
Высшего образования
«Сибирский федеральный университет»
ИНСТИТУТ ГОРНОГО ДЕЛА, ГЕОЛОГИИ И ГЕОТЕХНОЛОГИЙ
МАТЕМАТИКА
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников специальностей
Горное дело»
Семестра
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Ниже приведены таблицы номеров задач, входящих в задания на контрольные работы, по учебным планам. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его номера студенческого билета (шифр).
Студенты, изучающие математику 4 семестра, выполняют:
Контрольные работы № 1 (1 семестр).
Контрольные работы № 2 (2 семестр).
Контрольные работы № 3 (3 семестр).
Контрольные работы № 4 (4 семестр).
| Вариант | Контрольная работа №1 |
| Вариант | Контрольная работа №2 |
| Вариант | Контрольная работа №3 |
| Вариант | Контрольная работа №4 |
Элементы векторной алгебры
И аналитической геометрии
31 – 40. Привести уравнение кривой второго порядка к каноническому виду, построить график кривой.
31. x 2 + у 2 – 4x + 2у = 4; 32. x 2 – у 2 – 4у – 13 = 0;
33. x 2 – 4x + 2у + 2= 0; 34. x 2 + 4x + 4у 2 + 8у – 5 = 0;
35. x 2 – 6у 2 – 12x + 36у – 54 = 0; 36. 2x 2 + 4x + 18у 2 – 16= 0;
39. 3x 2 + 5у 2 + 12x – 10у + 2 = 0; 40. 4x 2 – 3у 2 – 8x – 6у – 11 = 0.
Элементы линейной алгебры
51 – 60. Дана система линейных уравнений
Доказать ее совместность и решить двумя способами: 1) по формулам Крамера; 2) методом Гаусса:
| 51. |  | 52. |  |
| 53. | 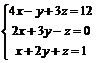 | 54. |  |
| 55. |  | 56. |  |
| 57. |  | 58. |  |
| 59. |  | 60. |  |
71 – 80. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 + z = 0.
| 71. |  | 72. |  | 73. |  |
| 74. | 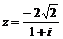 | 75. |  | 76. |  |
| 77. |  | 78. |  | 79. |  |
| 80. |  |
Введение в математический анализ
91 – 100.Найти пределы функций, не пользуясь правилом Лопиталя.
91. a) 

в) 


92. a) 

в) 
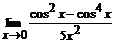

93. a) 

в) 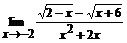

94. a) 

в) 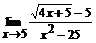


95. a) 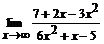
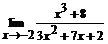
в) 


96. a) 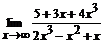

в) 


97. a) 

в) 


98. a) 

в) 
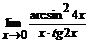

99. a) 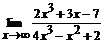

в) 


100. a) 

в) 


4. Производная и еЁ приложения
121 — 130. Найти производные 
| 121. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 122. | а)  ; ; | б) 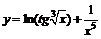 ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 123. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 124. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 125. | а)  ; ; | б)  ; ; |
в) 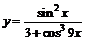 ; ; | г)  ; ; | |
д)  . . | ||
| 126. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 127. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 128. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д) 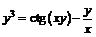 . . | ||
| 129. | а)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  . . | ||
| 130. | а)  ; ; | б)  ; ; |
в) 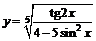 ; ; | г) 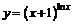 ; ; | |
д)  . . |
5. Приложения дифференциального
Исчисления
151 – 160. Исследовать методами дифференциального исчисления функцию 
151. 

153. 

155. 

157. 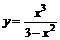

159. 

6. Дифференциальное исчисление функций
Нескольких переменных
161 – 170. Найти а) 

| 161. | a)  , , | б)  . . |
| 162. | а)  , , | б) 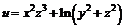 . . |
| 163. | а)  ; ; | б)  . . |
| 164. | а)  ; ; | б)  . . |
| 165. | а)  ; ; | б)  . . |
| 166. | а)  ; ; | б)  . . |
| 167. | а)  ; ; | б) 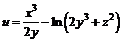 . . |
| 168. | а)  ; ; | б)  . . |
| 169. | а)  ; ; | б)  . . |
| 170. | а)  ; ; | б)  . . |
191 – 200. Даны функция 



191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
7. НеопределЁнный и определЁнный
Интегралы
201 – 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.
| 201. | a)  ; ; | б)  ; ; |
в) 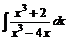 ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 202. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 203. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 204. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 205. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 206. | a)  ; ; | б) 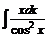 ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е) 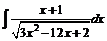 . . | |
| 207. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 208. | a)  ; ; | б)  ; ; |
в) 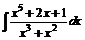 ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 209. | a) 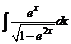 ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . | |
| 210. | a)  ; ; | б)  ; ; |
в)  ; ; | г)  ; ; | |
д)  ; ; | е)  . . |
211 – 220. Вычислить несобственный интеграл или доказать его расходимость.
| 211. | а)  ; ; | б).  . . |
| 212. | а)  ; ; | б).  . . |
| 213. | а)  ; ; | б).  . . |
| 214. | а)  ; ; | б).  . . |
| 215. | а)  ; ; | б).  . . |
| 216. | а) 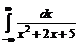 ; ; | б). 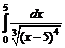 . . |
| 217. | а)  ; ; | б).  . . |
| 218. | а) 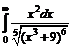 ; ; | б).  . . |
| 219. | а) 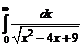 ; ; | . б).  . . |
| 220. | а)  ; ; | б).  . . |
Дифференциальные уравнения
231 – 240. Найти общее решение дифференциального уравнения.
| 231. | а)  ; ; | б)  . . |
| 232. | а)  ; ; | б)  . . |
| 233. | а)  ; ; | б)  . . |
| 234. | а)  ; ; | б)  |
| 235. | а)  ; ; | б)  . . |
| 236. | а)  ; ; | б)  |
| 237. | а)  ; ; | б)  . . |
| 238. | а)  ; ; | б)  . . |
| 239. | а)  ; ; | б)  . . |
| 240. | а)  . . | б)  . . |
251 – 260. Найти частное решение дифференциального уравнения 
y’ (0)=y’0. ( Задача Коша).
251. y» – y’ 

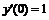
252. y» + y 

253. y» +7y’+12y = 
255. y»- 
256. y» + 9y 

257. y» – 4y’ +8y 
258. y» – 2y’ = 
259. y» +2y‘ +10y 

260. y» – 6y’ +9y = 
9. Кратные, криволинейные
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
http://poisk-ru.ru/s23921t10.html
http://mathdf.com/dif/ru/