Дифференциальное уравнение оси изогнутой балки
Для определения уравнения оси изогнутой балки воспользуемся законом Гука:
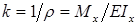
Выражение для кривизны некоторой кривой:
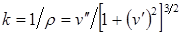
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому 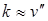
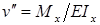
Продифференцировав полученное уравнение дважды по z, получим дифференциальное уравнение оси изогнутой балки : 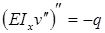
Интегрирование дифференциального уравнения оси изогнутой балки
Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.
Второе интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения изгибающего момента.
Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.
Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.
Постоянные интегрирования определяются из условий закрепления балки.
Метод интегрирования дифференциального уравнения изгиба балки
Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.
$EI\,y»(x) = M(x)$ – полученное дифференциальное уравнение;
$EI\,y'(x) = EI\,\varphi (x) = \int
$EI\,y(x) = \int
Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).
Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI\,\varphi (0) = C$, а прогиб $EI\,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.
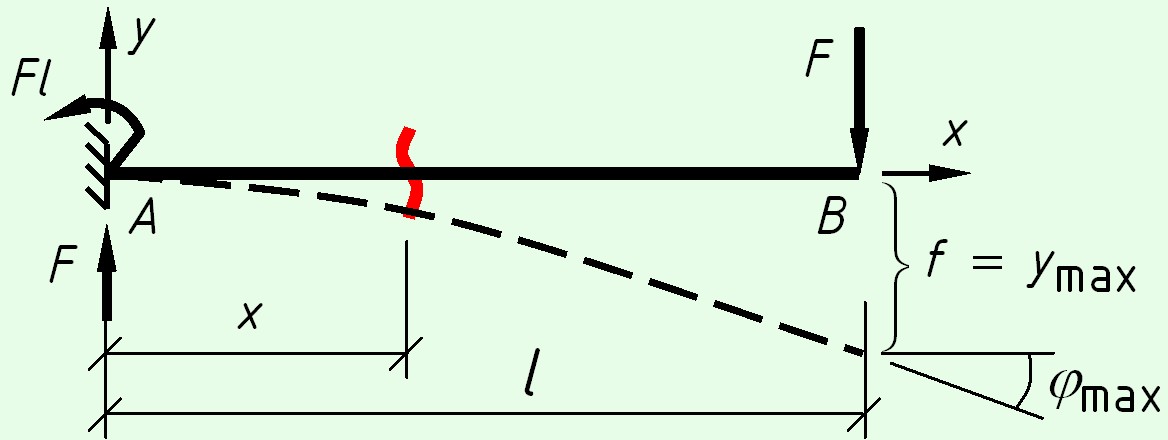
Консольная балка с силой на конце
На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F \cdot l$.
Уравнения изгибающих моментов
$M(x) = — Fl + Fx = F(x — l)$
Уравнение углов поворота
$EI\,y'(x) = EI\,\varphi (x) = \int
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$\left\ < \begin
Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = \frac<
Максимальный угол поворота сечения также будет иметь место при $x = l$
знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.
Шарнирно закрепленная балка с силой посередине
На опорах возникают вертикальные реакции $
Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид
$M(x) = \frac
Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l/2$
Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).
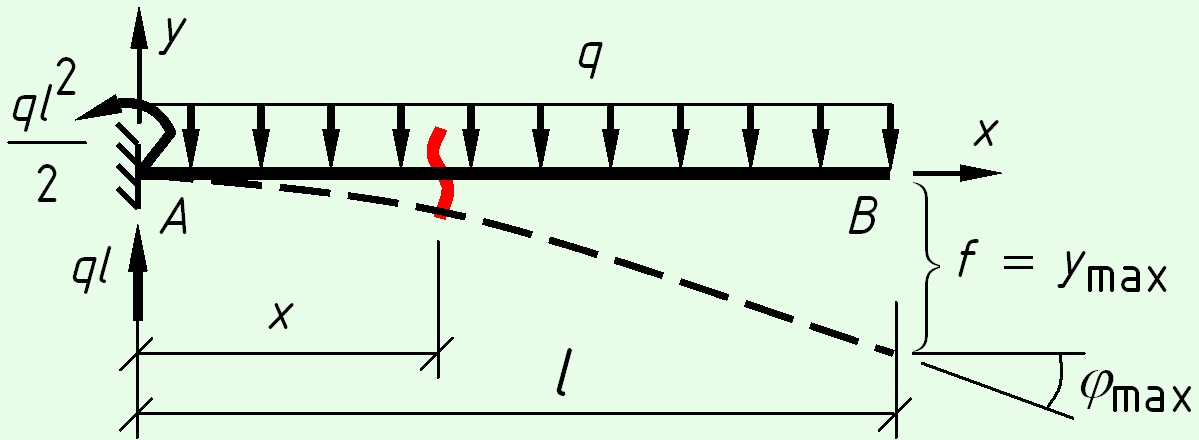
Консольная балка с равномерно распределенной нагрузкой
На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = \frac<
$M(x) = — \frac<
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$\left\ < \begin
Решение системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
Максимальный угол поворота сечения также будет иметь место при $x = l$
Дифференциальное уравнение изгиба балки на упругом основании
Определение постоянных при интегрировании дифференциального уравнения изгиба балки.
Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.
Приближенное дифференциальное уравнение упругой линии балки
Выбор знака в правой части определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и Mz противоположны — в правой части знак минус. Уравнение справедливо только в пределах применимости закона Гука.
Интегрируя, находим сначала углы поворота сечений
 , , |
а после второго интегрирования – прогибы балки
 . . |
25. Интегрирование дифференциального уравнения изгиба балки с несколькими участками.Метод Клебша.
Для составления уравнений необходимо выполнить следующие основные условия:
- начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
- интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
- при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z – a), где а – координата сечения, в котором приложен момент;
- в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления
Метод начальных параметров
Для углов поворота


где θ – угол поворота сечения; w – прогиб; θo – угол поворота в начале координат; w0 – прогиб в начале координат; dі – расстояние от начало координат до i-й опоры балки; ai – расстояние от начало координат до точки приложения сосредоточенного момента Mi; bi – расстояние от начало координат до точки приложения сосредоточенной силы Fi; сi – расстояние от начало координат до начала участка распределенной нагрузки qi; Ri и Мрi – реакция и реактивный момент в опорах балки.
Балка на упругом основании
 Рис.10.1 Рис.10.1 | В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований « 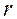 » » |
зависит от прогибов « 


Здесь: 


Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса

Обычно 

Дифференцируя один раз (3) с учетом (4) получим
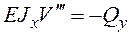
Дифференцируя (5) с учетом (4) найдем

Подставим (2) в (6)
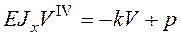
Обозначим
Тогда уравнение (7) примет вид

Это дифференциальное уравнение балки на упругом основании.
Дифференциальное уравнение изгиба балки на упругом основании
 Рис.10.1 Рис.10.1 | В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований «  » » |
зависит от прогибов « 

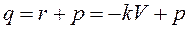
Здесь: 


Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса

Обычно 

Дифференцируя один раз (3) с учетом (4) получим

Дифференцируя (5) с учетом (4) найдем

Подставим (2) в (6)
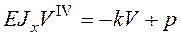
Обозначим
Тогда уравнение (7) примет вид

Это дифференциальное уравнение балки на упругом основании.
http://sopromat.xyz/lectures?node=1966
http://allrefrs.ru/2-23004.html