Дифференциальные уравнения для скорости и ускорения

Интегрирование дифференциальных уравнений прямолинейного движения материальной точки

Краткое изложение результатов

Здесь мы кратко изложим основные результаты, полученные при интегрировании дифференциальных уравнений прямолинейного движения материальной точки. Далее следует их подробное изложение.

Сила, зависящая от времени

Если на материальную точку действует сила, зависящая от времени , то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид:
.
Вводим ускорение и интегрируем это уравнение.
.
Здесь и далее A и B – произвольные точки на оси Ox . Заменим . Получаем закон изменения скорости от времени:
.
Интегрируя уравнение , получаем закон движения точки :
;
.

Сила, зависящая от скорости

Пусть на точку действует сила, зависящая от скорости . Составляем дифференциальное уравнение движения и интегрируем его:
.
Последнее уравнение дает в неявном виде зависимость . Решаем его. После чего интегрируем уравнение , как описано выше.

Есть второй способ интегрирования уравнения движения в случае зависимости силы от скорости. Для этого переходим от переменных x и t к переменным и x . Считаем, что скорость является функцией от координаты x :
;
.
Последнее уравнение дает в неявном виде зависимость . Далее интегрируем уравнение :
.
Это уравнение дает в неявном виде закон движения точки .

Сила, зависящая от перемещения

Пусть на точку действует сила, зависящая от перемещения . Составляем уравнение движения, переходим от переменных x и t к переменным и x , и интегрируем полученное дифференциальное уравнение:
;
;
.
Это уравнение представляет собой закон сохранения механической энергии для прямолинейного движения. Из него находим зависимость скорости от перемещения . После чего интегрируем уравнение , как это описано выше.

Дифференциальное уравнение движения точки

Рассмотрим прямолинейное движение материальной точки, находящейся под действием постоянных и переменных сил. Направим ось Ox системы координат вдоль линии движения точки. Пусть на нее действуют n сил, проекции которых на ось Ox мы обозначим как . Положение точки, при прямолинейном движении, однозначно определяется ее координатой x . Нам нужно определить закон движения точки , то есть закон изменения ее координаты со временем.

Уравнение движения точки определяется вторым законом Ньютона, который в случае прямолинейного движения имеет вид:
(1) .

Вместо того, чтобы в каждом уравнении выписывать все n сил, введем их равнодействующую, проекция которой, на ось x равна сумме проекций всех сил на эту ось:
.
Тогда задача сведется к движению материальной точки под действием одной силы . При этом уравнение движения примет наиболее простой вид:
(2) .
В дальнейшем, проекцию равнодействующей мы будем называть просто силой, действующей на точку.

Сила может быть как постоянной, так и зависеть от времени t , координаты x и от скорости . К сожалению, если зависит от всех перечисленных факторов, то не всегда возможно решить уравнение (2) аналитически. Поэтому мы рассмотрим те случаи, когда возможно получить аналитическое решение этого уравнения. Заметим, что если сила является постоянной, то уравнение (2) можно решать любыми, приводимыми ниже, способами.

Почему мы обозначаем в виде проекции силы на ось x , хотя рассматриваем только движение вдоль одной оси? – Потому что под обозначением силы R в виде одной буквы, часто подразумевается ее абсолютная величина: . Она имеет неотрицательные значения: . А когда мы пишем силу как проекцию , то подразумеваем, что эта величина может быть как положительной (если сила направлена вдоль оси x ), так и отрицательной (когда она направлена противоположно оси x ). В теоретической механике, в подобных случаях, иногда также говорят, что есть алгебраическое значение силы. Это относится не только к силе, ни и ко всем другим, рассматриваемым далее, векторным величинам.

Интегрирование уравнения движения с силой, зависящей от времени

Вначале рассмотрим случай, когда задан закон изменения силы со временем: . Перепишем уравнение (2), явно указав эту зависимость:
(t1) .

В этом уравнении время t является независимой переменной; координата x – зависимой переменной; – это вторая производная координаты по времени: . Масса m – это постоянная, то есть заданное число. С математической точки зрения, уравнение (t1) есть дифференциальное уравнение второго порядка, не содержащую зависимую переменную x в явном виде.

Решение такого уравнения выполняется с помощью подстановки
.
Тогда
.
Подставляя в (t1), мы получаем дифференциальное уравнение первого порядка:
(t2) .
Выполняя подстановку, мы ввели новую переменную , равную производной координаты x по времени t . Эта производная является проекцией скорости точки на ось Ox . Таким образом, процесс решения разбивается на две части. Сначала мы, решаем уравнение (t2), и находим закон изменения скорости со временем: . Затем, используя уравнение , находим закон изменения координаты .

Упростим уравнение (t2), разделив его на массу m :
(t3) ,
где – ускорение точки. Поскольку зависимость силы от времени известна, то и зависимость ускорения от времени также известна.

Уравнение (t3) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем.
;
(t4) ;
(t5) .
Здесь – постоянная интегрирования. Чтобы ее определить, нужно знать значение скорости в какой-либо момент времени . Если мы сможем выразить интеграл через известные функции, то подставив в (t5) значения времени и значение скорости в этот момент, мы сможем определить постоянную .

Для простых задач, формула (t5) вполне удобна. Но если интеграл не выражается через известные функции, то выполнить численное интегрирование по этой формуле нельзя. Поэтому найдем закон изменения скорости со временем в более удобном виде.

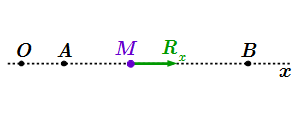
Прямолинейное движение точки M под действием силы R_x.

Пусть нам известно, что в момент времени , точка M находилась в положении A, имела координату и скорость . Рассмотрим произвольный момент времени . Пусть в этот момент времени точка M находится в положении B, с координатой и скоростью . Величины и нам пока не известны. Наша задача их найти.

Перепишем (t4) явно указав, что есть функция от t :
(t6) .
Интегрируем (t6) от момента времени до :
.
Слева – интеграл от полного дифференциала. Поэтому он интегрируется элементарно:
.
Здесь мы учли, что . В результате получаем:
;
.

Этот результат можно получить и несколько иначе, если в интеграле сразу перейти к переменной . Тогда пределы интегрирования станут и . В результате получим тоже самое:
.

Итак, мы нашли значение скорости в произвольный момент времени :
(t7) .
Заменим обозначение момента времени на t . В результате получим закон изменения скорости со временем t :
(t8) .

Интеграл справа записан не вполне корректно, хотя так часто пишут. Рассмотрим пример определенного интеграла . Он зависит от пределов интегрирования a и b , но не зависит от переменной интегрирования t . Можно сказать, что переменная t принимает заданные значения из отрезка , которые применяются только для вычисления интеграла. Поэтому для переменной интегрирования t можно использовать любое обозначение. Например, можно использовать переменную . Тогда .

В (t8) мы использовали одно и то же обозначение, как для верхнего предела интеграла, так и для переменной интегрирования. Это может привести к путанице. Поэтому используем для переменной интегрирования любое другое, не используемое обозначение, например . Тогда формула (t8) примет следующий вид:
(t9) .

Теперь найдем закон изменения координаты x от времени. Интегрируем уравнение
.
Разделяем переменные:
(t10) .
Здесь мы также можем выполнить интегрирование от A до B, но мы продемонстрируем другой способ, как получить результат в удобном виде, применяя неопределенный интеграл. Поскольку неопределенный интеграл определен с точностью до постоянной, то запишем его с нижним пределом интегрирования . Интегрируем (t10):
(t11) .
Найдем значение постоянной интегрирования . Для этого подставим сюда :
.
Далее учитываем, что значение координаты точки в момент времени нам известно: . Также учитываем, что интеграл в правой части имеет равные пределы интегрирования и поэтому равен нулю. В результате получаем:
.
Отсюда находим значение постоянной интегрирования: . В результате получаем закон движения точки:
(t12) .

Итак, мы нашли, что если на точку действует сила , то для определения ее закона движения, нужно сначала определить закон изменения скорости со временем:
(t7) .
А затем определить закон движения:
(t12) .
При этом мы полагаем, что нам известны скорость и координата в некоторый момент времени . Если бы мы проводили интегрирование через неопределенные интегралы в общем виде, то и были бы постоянными интегрирования и .

Постоянная сила

Разберем случай, когда действующая на точку сила имеет постоянное значение: . В этом случае ускорение также постоянно: . Интегрируем, используя таблицу неопределенных интегралов. Из (t7) находим закон изменения скорости со временем:
;
(t14) .
Мы видим, что скорость линейно изменяется со временем.

Подставляем в (t12) и находим закон движения точки:

;
(t15) .

Если в начальный момент времени , скорость точки была , а координата , то . Из (t14) и (t15) получаем:
;
.

Равномерное движение

Если проекция силы на ось Ox равна нулю: , то ускорение также равно нулю: . В этом случае из (t14) находим, что скорость точки постоянна:
.
Из (t15) находим, что координата линейно меняется со временем:
.

Если в начальный момент времени , скорость точки была , а координата , то ;
;
.

Интегрирование уравнения движения с силой, зависящей от скорости

Разберем случай прямолинейного движения материальной точки, когда действующая сила зависит от скорости . Такие задачи встречаются при движении в жидкой или газообразной среде, когда на точку помимо постоянных сил, действует сила трения, зависящая от скорости. В этом случае, уравнение движения имеет вид:
(v1) .
Разделим обе части уравнения на массу m :
(v2) ,
где – ускорение точки. Теперь нам известна зависимость ускорения точки от ее скорости. Уравнение (v2) не содержит в явном виде как зависимую переменную x , так и независимую переменную t . Поэтому его можно решать двумя способами.

Решение уравнения, определяя v_x(t)

Применим к уравнению (v2) метод решения дифференциального уравнения, не содержащего зависимую переменную в явном виде. Для этого, как и в предыдущем случае, делаем подстановку
.
Тогда
.
Подставляя в (v2), мы получаем дифференциальное уравнение первого порядка:
(v3) .

Пусть, как и в предыдущем случае, в момент времени , точка находилась в положении A, имела координату и скорость . И пусть в произвольный момент времени , точка находится в положении B с координатой и скоростью . Нам нужно найти величины и .

Разделяем переменные.
;
.
Перепишем это уравнение, указав, что скорость является функцией от времени:
.
Интегрируем по времени от до :
.
В левой части сделаем замену переменной. От переменной t перейдем к переменной . При этом изменим пределы интегрирования учитывая, что при ; и при :
(v4) .

Заменим обозначения переменных , и переменной интегрирования . Подставим в (v4):
(v5) .
Это уравнение, в неявном виде, дает закон изменения скорости от времени t . Вычислив интеграл, и выполнив преобразование, мы можем выразить через t : .

Далее, по формуле (t12) ⇑ определяем закон движения материальной точки:
(t12) .

Решение уравнения, определяя v_x(x)

Выпишем уравнение (v2) еще раз.
(v2) .
Для применения этого метода, в качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . То есть считаем, что скорость является функцией от координаты: .

Выразим через переменные x и вторую производную координаты по времени:
.
Подставим в (v2) и разделяем переменные:
;
.
В левой части в явном виде запишем как функцию от x , и интегрируем по x от положения A до B:
;
.
В интеграле слева переходим от переменной x к :
(v6) .

Переобозначим переменные:
(v7) .
Это уравнение дает в неявном виде зависимость скорости от координаты:
.
Подставив сюда , получим для x дифференциальное уравнение первого порядка. Решаем его методом разделения переменных:
;
.
Интегрируем от положения A до B:
;
.
Заменим переменные:
(v8) .

Уравнение (v8) дает в неявном виде закон движения материальной точки .

Интегрирование уравнения движения с силой, зависящей от перемещения

Наконец рассмотрим случай прямолинейного движения материальной точки, когда действующая сила зависит от перемещения x . Такие задачи встречаются при движении в потенциальных полях – в гравитационных или электрических. Сюда также относится движение груза, прикрепленного к упругой пружине.

Выписываем уравнение движения для этого случая:
(x1) .
Это дифференциальное уравнение второго порядка. Оно не содержит независимую переменную t в явном виде. Также как и в предыдущем случае, применяем метод решения дифференциального уравнения, не содержащего независимую переменную в явном виде.

Перейдем к новым переменным. В качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . Считаем, что скорость является функцией от координаты: .

Выразим вторую производную координаты по времени через переменные x и :
;
Подставим в (x1) и разделяем переменные:
(x2) ;
.
Интегрируем по x от A до B:
(x3) .
Вычисляем интеграл, используя таблицу неопределенных интегралов:
;
.
Подставляем в (x3):
(x4) . Нетрудно видеть, что слева стоит изменение кинетической энергии материальной точки. Справа – работа, которую совершает сила при перемещении материальной точки из A в B. Само уравнение (x4) представляет собой теорему об изменении кинетической энергии точки для прямолинейного движения.

Вернемся снова к уравнению (x2).
(x2) .
Его можно проинтегрировать и другим способом.

Для этого представим правую часть в виде производной по координате:
,
где – координата произвольной заранее выбранной точки C .
Левую часть также представим в виде производной по координате:
.
Тогда (x2) можно записать в виде:
.

Поскольку производная по x от выражения в скобках равна нулю, то само выражение является постоянной, не зависящей от x величиной:
.
Такая форма записи, когда некоторая функция от переменных приравнивается постоянной, называется интегралом дифференциального уравнения. Перепишем его в следующем виде:
(x5) .
Здесь – кинетическая энергия точки; – потенциальная энергия, отсчитываемая от, произвольным образом выбранной, точки C ; E – постоянная интегрирования, которая в данном случае имеет определенный физический смысл – это полная механическая энергия материальной точки. Поэтому мы ее обозначили привычной для этого случая буквой E . Само уравнение (x5) представляет собой закон сохранения механической энергии. С математической точки зрения, энергия E является интегралом дифференциального уравнения, или, как говорят в механике, интегралом движения точки. То есть величиной, сохраняющей при движении постоянное значение.

Выше мы пришли к выводу, что постоянная интегрирования E не зависит от координаты x , но ничего не сказали о ее зависимости от времени. Однако, для одномерного движения, со временем может изменяться только одна координата x . Поскольку постоянная E от нее не зависит, то она не зависит также и от времени t . Поэтому полная механическая энергия сохраняет постоянное значение и в различные моменты времени.

Нетрудно видеть, что формулировки (x4) ⇑ и (x5) ⇑ эквивалентны. Для доказательства, приравняем механическую энергию точки для двух положений A и B:
;

.
Здесь мы разбили интеграл от до на два интеграла – от до ; и от до . Интегралы от до сократились.

Найдем зависимость скорости точки от координаты. При этом мы считаем, что скорость точки в положении A нам известна. Рассмотрим два положения: A и B. Из (x4) ⇑ имеем:
,
где – работа, которая производит сила при перемещении точки из A в B. Наконец, заменим на x , и на . В результате получим искомую зависимость:
(x6) ,
где – работа, которая производит сила при перемещении материальной точки из A в точку с координатой x . Скорость определена с точностью до знака (плюс или минус). Знак нужно выбирать из начальных условий и исследования движения. Если в точке , то при достаточно малых значениях . Далее точка может остановиться и начать движение в обратную сторону. Тогда нужно выбрать знак минус, чтобы скорость стала отрицательной.

Теперь, зная зависимость , находим закон движения материальной точки. Для этого интегрируем уравнение:
;
;
;
.
Это уравнение дает в неявном виде зависимость координаты x от времени t .

Приложение к движению в пространстве

Приведенные выше результаты могут быть применимы и для некоторых случаев движения материальной точки в двухмерном или трехмерном пространстве.

Пусть нам известно, что в момент времени , материальная точка находилась в точке A, и имела скорость . Выберем трехмерную систему координат Oxyz , и распишем эти начальные условия по компонентам:
При ;
При ;
При .

Сила в пространстве, зависящая от времени

Пусть на материальную точку действует сила, зависящая от времени: . Составим уравнения ее движения:
.

Выпишем уравнение для координаты x с начальными условиями:
; при .
Здесь все необходимые величины известны, и они не зависят от значений других координат. Мы можем найти закон изменения координаты x со временем, применяя интегрирование уравнения движения с силой, зависящей от времени ⇑ для прямолинейного движения.

Выпишем уравнение для координаты y с начальными условиями:
; при .
Здесь также известны все необходимые величины, и они не зависят от значений других координат. Мы также можем найти закон изменения координаты y со временем, применяя интегрирование, как для прямолинейного движения.

Точно также мы можем найти закон изменения координаты z со временем. В этом случае говорят, что переменные разделились. Уравнения движения, составленные для каждой из координат, вместе с начальными условиями, не зависят от значений других координат. Поэтому каждое такое уравнение можно проинтегрировать отдельно. В результате мы получим закон движения материальной точки в трехмерном случае: .

Силы, приводящие к разделению переменных

Пусть теперь на точку действуют три взаимно перпендикулярные силы. И пусть одна из них зависит только от времени; вторая – от проекции скорости на направление силы; третья – от проекции радиус-вектора на направление силы.

Выберем систему координат Oxyz , оси которой направим вдоль направлений действующих сил. Тогда в этой системе координат отличными от нуля будут только три проекции сил: . Составляем уравнения движения:
;
;
.
Мы видим, что и в этом случае переменные разделились. Каждое из этих уравнений зависит только от одной переменной. И мы можем решить его, применяя изложенные выше методы. Все это применимо и к случаю, когда любая из этих сил является постоянной.

И, разумеется, тут могут быть различные вариации, приводящие к разделению переменных. Например, если зависящая от времени сила лежит в плоскости xy , а перпендикулярная ей сила зависит только от координаты z . В этом случае переменные также разделяются.

Автор: Олег Одинцов . Опубликовано: 12-10-2020

Дифференциальные уравнения, общие понятия

Дифференциальные уравнения — это отдельный вид функциональных уравнений. А значит для дифференциальных уравнений такие понятия, как функция, аргумент функции, область определения функции и т.п., также являются актуальными.

Главное отличие дифференциальных уравнений от фунцкциональных в том, что одна из переменных (как правило искомая неизвестная величина) является производной или дифференциалом функции, аргументом которой является вторая переменная, впрочем аргументов у функции может быть несколько.

В общем случае определение дифференциального уравнения может выглядеть так:

Дифференциальным уравнением называется равенство между функцией и ее производной или дифференциалом.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного аргумента. Например:

у’ = f(x) (539.1)

Напомню, функциональное уравнение может иметь следующий вид:

у = f(x) (538.1)

Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких аргументов. Например:

у’ = f(x₁,x₂) или у’ = f(x,u) (539.2)

где х₁, х₂ или х, u — возможные обозначения для различных аргументов функции.

Порядком дифференциального уравнения считается порядок наивысшей производной, входящей в уравнение. Например уравнение (539.1) является уравнением первого порядка. Уравнение второго порядка может иметь вид:

y» = f(x) (539.3)

Решением дифференциального уравнения является функция, подставление которой вместо неизвестной функции обращает уравнение в тождество. Другими словами уравнение становится равенством.

А теперь эти общие математические понятия (кстати тут приведены далеко не все основные понятия) попробуем описать простым человеческим языком, но начать придется издалека.

Производная функции

Мы живем в несовершенном, постоянно изменяющемся мире. Все течет, все изменяется, как подметил еще Гераклит. Однако в древности были и другие мыслители, которые в отличие от Гераклита пытались этот мир как-то понять и оценить. Так далеко в историю мы заглядывать не будем, хотя предпосылки к дифференциальному исчислению следует искать именно там, а ограничимся простыми и наглядными примерами:

Пример 1

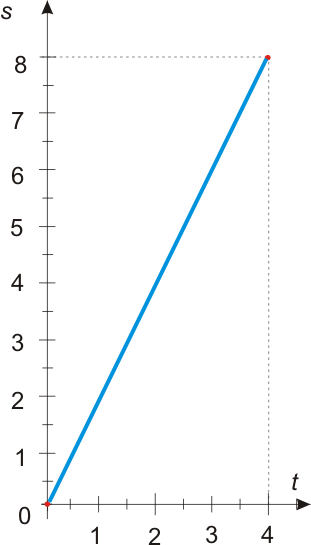
Мы вышли из пункта А в пункт Б и находились в пути 4 часа, каждый час мы проходили по 2 километра. Вопрос: какое расстояние между пунктами А и Б?

Вообще это задачка для 3-4 класса начальной школы и решить ее вроде бы не сложно (потому я ее и выбрал): достаточно сложить все расстояния, пройденные за каждый час, а так как эти расстояния одинаковые, то можно еще больше упростить задачу, умножив на 4 расстояние, пройденное за один промежуток времени. Таким образом расстояние между пунктами А и Б составляет:

2 км · 4 = 8 км (539.4)

А между тем условия задачи можно рассматривать и по другому, т.е. как зависимость пройденного расстояния от времени. В этом случае у нас время -независимая переменная t или аргумент функции, а пройденное расстояние — значение функции в тот или иной момент времени или переменная s. Тогда условия задачи соответствуют следующему функциональному уравнению:

s = f(t) = 2t (539.5)

а также графику этой функции:

Рисунок 539.1. График функции f(t) = 2t.

Так если по оси t откладывать промежутки времени Δt (ч), которое мы были в пути, а по оси s — преодоленное за эти промежутки времени расстояние Δs (км), то график указанной функции будет иметь такой вид, как показано на рисунке 539.1. В общем случае используются более привычные оси х и у, соответственно рассматриваются функции вида y = f(x), но сути дела это никак не меняет.

Решая уравнение (539.5) мы можем определить не только общее расстояние, преодоленное за 4 часа пути, но и в любой интересующий нас момент времени. Например, нас интересует, какое расстояние мы прошли за 1.5 часа. Согласно уравнению (539.5) это расстояние составит 2·1.5 = 3 километра.

А если нас интересует не расстояние, преодоленное к тому или иному моменту времени, а скорость движения? Можем ли мы определить эту скорость на основе имеющихся данных?

Оказывается можем, потому что скорость — это тоже функция, которая в свою очередь также зависит от времени.

Так как каждый час мы преодолевали по 2 км, то отсюда можно сделать вывод, что скорость нашего движения была постоянной, тогда по давно известному нам уравнению, описывающему движение с постоянной скоростью:

v = s/t = 8/4 = 2 км/ч (539.6)

В данном случае, так как скорость постоянная, не имеет значения, на каком временном промежутке мы эту скорость определяем. Тем не менее рассмотрим данную ситуацию с точки зрения математики.

Временные промежутки, когда засекалось пройденное расстояние, мы обозначим как Δt = 1, соответственно t = ΣΔt = 1 + 1 + 1 + 1 = 4. Расстояния, пройденные за эти промежутки времени обозначим как Δs = 2. На графике функции это будет выглядеть так:

Рисунок 539.2

С точки зрения математики временные промежутки Δt — это приращение аргумента функции:

Δt = t — t₀ (539.7)

Соответственно расстояния, пройденные за рассматриваемый промежуток времени — это приращение функции:

Δs = Δf(t) = f(t) — f(t₀) (539.8)

А так как использовать греческую литеру Δ не всегда удобно (в частности мне для этого приходится заходить в отдельный редактор текста, а наборщикам в типографиях вставить эту литеру было еще сложнее), то часто приращение значения искомой функции и приращение аргумента функции обозначают как ds и dt.

Тогда формулу определения скорости можно записать так:

v = ds/dt (539.9)

Таким образом мы с одной стороны вроде бы просто разделили расстояние на время — задача для 3-4 класса, а с другой стороны мы определили производную функции s = f(t), соответствующим образом ее продифференцировав, а это уже задача курса алгебры, а то и высшей математики.

Возможно и не стоило это так подробно расписывать, но на мой взгляд это очень важно, чтобы показать, что в дифференциальном исчислении нет ничего трудного, если рассматривать его на соответствующих примерах.

Итак скорость v является производной функции s = f(t) = 2t. Дифференциальное уравнение в этом случае будет выглядеть так:

v = s’ = f'(t) (539.10.1)

v = (2t)’ = 2 (539.10.2)

Но и это еще не все, на основании имеющихся данных: времени в пути и расстояний, преодоленных за 1 час, мы можем определить ускорение нашего движения.

Так как скорость нашего движения оставалась постоянной, соответственно dv = 0, то само собой и ускорения никакого не было, ни положительного ни отрицательного. Другими словами ускорение нашего движения составляло а = 0 км/ч 2 .

На языке математики это будет выглядеть так:

а = v’ = dv/dt = s» = d 2 s/dt 2 (539.11.1)

a = 0/1 = (2t)» = (2)’ = 0 (539.11.2)

Т.е. в данном случае для определения ускорения нужно определить первую производную функции скорости (уравнения, выражающего зависимость скорости от времени) или вторую производную функции расстояния (уравнения, выражающего зависимость пройденного расстояния от времени).

На основании вышеизложенного мы можем дать следующее предварительное определение производной:

Производная — это скорость изменения функции

В рассмотренном выше примере скорость движения — это скорость изменения функции расстояния, а ускорение — это скорость изменения функции скорости. Если бы мы все 4 часа сидели на месте, то и расстояние, пройденное нами, было бы равно нулю, и скорость и ускорение, но даже для такого случая можно записать соответствующие дифференциальные уравнения:

Однако в жизни гораздо чаще встречаются функции, даже третьи производные которых не равны нулю.

Рассмотрим другой пример все с тем же движением, на этот раз чуть более сложный.

Пример 2

По ровной наклонной поверхности скатывается шар. Начальная скорость движения равна v_o = 0. Определить пройденное шаром за 4 секунды расстояние, скорость после 1, 2, 3 и 4 секунд движения и постоянное ускорение движения, если за первую секунду шар преодолел расстояние 3 м, за вторую — 9 м, за третью — 15 м, за четвертую — 21 м.

С определением пройденного расстояния по прежнему проблем нет: достаточно сложить расстояния, которые преодолел шар за каждую секунду s = ΣΔs = 3 + 9 + 15 + 21 = 48 метров. А вот скорость и ускорение в данном случае определить не так просто. Тем не менее попробуем.

Если воспользоваться полученными раннее знаниями, то вроде бы в первый промежуток времени скорость должна быть равна:

Вот только в данном случае у нас скорость — изменяющаяся величина, зависящая от времени, поэтому результат полученный при решении уравнения (539.12) можно рассматривать лишь как среднюю скорость движения на первом участке. Тогда более правильно уравнение скорости на первом участке записать так:

v_1ср = ds₁/dt₁ = 3/1 = 3 м/с (539.12.2)

Подобным образом мы достаточно легко можем определить среднюю скорость на всех участках пути, и она составит v_2ср = 9 м/с, v_3ср = 15 м/с, v_4ср = 21 м/с, но в данном случае нас интересует не среднее значение функции скорости на рассматриваемом участке, а значение функции скорости во вполне определенной точке, т.е. после 1, 2, 3 и 4 секунд движения. Как это сделать?

По условиям задачи ускорение — производная от скорости — является постоянной величиной, т.е. скорость изменения скорости будет постоянной. В этом случае значение средней скорости является средним арифметическим от начальной и конечной скорости на рассматриваемом участке:

тогда при v_o = 0

v₁ = 3·2 = 6 м/с (539.13.2)

Соответствующим образом мы можем определить значения скорости и в остальных точках, например (6 + v₂)/2 = 9, v₂ = 9·2 — 6 = 12 м/с; (12 + v₃)/2 = 15, v₃ = 15·2 — 12 = 18 и так далее, а теперь переведем полученные данные на язык высшей математики. Мы видим, что v₁ = 6·1, v₂ = 6·2 = 12, v₃ = 6·3 = 18, т.е. значение скорости явно зависит от времени, соответственно уравнение скорости мы можем записать следующим образом:

v = s’ = 6t (539.14)

Соответственно ускорение движения шара составит:

a = v’ = (6t)’ = 6 м/с 2 (539.15)

Между тем, если бы нам были заданы меньшие значения временных промежутков и соответственно меньшие значения пройденных расстояний за эти промежутки времени, например при dt₁ = 1 секунда, ds₁ = 3 м, dt₂ = 0.1 секунды и ds₂ = 0.63 м, то средняя скорость на рассматриваемом втором участке составила бы v_2ср = ds/dt = 0.63/0.1 = 6.3 м/с, а скорость в в точке t₂: v_2сp = (6 + v₂)/2 = 6.3, v₂ = 12.6 — 6 = 6.6 м/с. Т.е. закономерность изменения значения скорости никуда не девается, тем не менее, чем меньше рассматриваемый временной промежуток dt, тем меньше разница между значением средней скорости изменения функции и скоростью изменения функции в рассматриваемой точке. Из этого можно сделать еще один очень важный вывод:

Скорость изменения функции может быть разная. Чем меньше приращение аргумента функции dt, тем ближе значение среднего изменения скорости к изменению скорости функции в рассматриваемой точке.

На основании этого можно сформулировать более полное определение производной функции:

Производная функции в точке — это скорость изменения функции в рассматриваемой точке при стремлении приращения аргумента функции к нулю (Δt → 0)

Поэтому иногда производную называют мгновенной скоростью изменения функции. В нашем случае уравнение производной будет выглядеть так:

(539.16)

На данном этапе вид формулы (539.16) нас уже не пугает (во всяком случае мне так кажется). Совсем другое дело, когда подобная формула приводится в начале темы, посвященной рассмотрению производных функции.

Дифференциал (первообразная) функции

С задачей определения скорости и ускорения в примере 2 мы вроде бы справились и даже составили соответствующие уравнения (539.14) и (539.15). Но иногда требуется решить и обратную задачу — например определить исходное уравнение, описывающее зависимость перемещения от времени.

Если скорость является производной функции расстояния v = s’, то расстояние при этом является первообразной (дифференциалом) функции скорости s = ∫v. Процесс нахождения первообразной функции называется интегрированием. Так, чтобы получить уравнение зависимости пройденного расстояния от времени, нам нужно проинтегрировать уравнение скорости. При этом уравнение расстояния более правильно записывать так

s = ∫vdt (539.17)

В общем случае интегрирование может быть более сложной задачей, чем дифференцирование, потому что функции бывают не только степенными, как в данном примере, но и тригонометрическими, обратными тригонометрическими и т.п., но пока нас интересует, как проинтегрировать простую степенную функцию вида f(t) = 6t.

Вообще-то мы могли сразу построить график, отражающий зависимость пройденного расстояния от времени по данным примера 2, тем не менее сделаем это сейчас, а заодно построим график для уравнений скорости и ускорения и расположим их в такой последовательности:

Рисунок 539.3. Графики степенных функции а) а= 6, б) v = at, в) s = at 2 /2.

Как видим, график, отражающий зависимость ускорения от времени, у нас самый простой. Ускорение постоянное, а = 6 м/с 2 и от времени никак не зависит. Тем не менее, зная ускорение, мы можем определить скорость движения в любой точке времени. Так из уравнений (539.14) и (539.15) следует, что:

v = 6t = at (539.14.2)

Соответственно решая это уравнение, мы можем определить скорость в любой момент времени.

Но если рассматривать это действие с точки зрения геометрии, то мы, умножая ускорение на время, определяем площадь прямоугольника со сторонами а = 6 и t. При t = 4 площадь прямоугольника составит 6·4 = 24, точнее 24 м/с так как мы все-таки определяем скорость.

Если мы построим график, отражающий зависимость изменения скорости от времени, то увидим, что на этом графике значения скорости в той или иной момент времени соответствуют площадям прямоугольника со сторонами а = 6 и t.

Получается, что если определить площадь треугольника со сторонами v и t, то это и будет расстояние, преодоленное к тому или иному промежутку времени:

s = vt/2 = at 2 /2 = 6t 2 /2 = 3t 2 (539.18)

Уравнение (539.18) можно записать как дифференциальное:

s = ∫6tdt = 3t 2 (539.18.2)

Если график, показанный на рисунке 539.3.в) также является графиком для производной некоторой функции, то для определения первообразной этой функции нам также следовало бы найти площадь фигуры, ограниченной квадратной параболой.

Сделать это в принципе не сложно, так как площадь фигуры, очерченной квадратной параболой таким образом, как показано на рисунке 539.3.в) в 3 раза меньше площади прямоугольника со сторонами s и t, соответственно S = st/3 = 3t 2 t/3 = t 3 и эту процедуру можно повторять до бесконечности.

Почему площадь фигуры, ограниченной квадратной параболой именно в 3 раза меньше, чем площадь прямоугольника, а площадь фигуры ограниченной кубической параболой в 4 раза меньше площади прямоугольника, я здесь объяснять не буду, тем не менее такая закономерность существует и в математическом выражении выглядит так:

∫aх n dx = ax n+1 /n + C (539.19)

В данном случае С — это некоторая постоянная величина. Как мы выяснили, при дифференцировании постоянные величины обращаются в нуль, как пример — уравнение (539.11.2), соответственно решая обратную задачу, т.е. интегрируя функцию, мы допускаем, что некая постоянная величина в первообразной функции была.

Например в общем случае уравнение скорости (539.14.2) должно выглядеть так:

v = v_o + at (539.14.3)

где v_o — это и есть некая постоянная величина. В нашем случае по условиям задачи v_o = 0, поэтому мы использовали сокращенную форму записи.

Определенный интеграл

В общем случае график функции может выглядеть как угодно, например так:

Рисунок 539.4

В этом случае сразу определить площадь фигуры, ограниченной графиком функции, не получится. Но мы можем разбить эту фигуру на участки шириной Δх и определить среднее значение у для каждого участка. Теперь определить площади трех прямоугольников большого труда не составит, вот только суммарная площадь прямоугольников не будет равна площади фигуры, ограниченной графиком функции:

S ≈ ∑y_iΔx (539.20)

Но чем больше будет у нас прямоугольников с шириной Δх, т.е, чем меньше будет значение Δх, тем точнее будет значение у, а значит и суммарная площадь прямоугольников будет ближе к площади фигуры, ограниченной графиком функции.

При интегрировании, как и при дифференцировании для получения более точного результата приращение аргумента функции должно стремиться к нулю (maxΔx → 0) .

Из этого можно сделать следующий вывод:

Если существует предел суммы, определяемой по формуле (539.20) вне зависимости от количества прямоугольников и при стремлении ширины прямоугольников к нулю, то такой предел называется определенным интегралом, а суммы, определяемые по формуле (539.20) — интегральными суммами.

Так как на рисунке 539.4 показан график непрерывной функции, то такая функция является интегрируемой и для определения дифференциала функции используется определенный интеграл. При этом 0 и 3 — это пределы интегрирования.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Уравнения, основные понятия

Оценка пользователей:10.0 (голосов: 1)Переходов на сайт:1701Комментарии:

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Техническая механика

Динамика

Принцип независимости действия сил

Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности .

Пусть к материальной точке А приложены силы F₁ и F₂ равнодействующая которых равна F на основании аксиомы параллелограмма запишем:

Разделив обе части равенства на массу точки m , получим:

Применяя последовательно аксиому параллелограмма, можно показать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила F = ΣF_i .

Пользуясь изложенным выше принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.

Дифференциальные уравнения движения материальной точки

Пусть материальная точка А массой m движется в плоскости чертежа под действием равнодействующей силы F = ΣF_i с ускорением а , тогда:

Спроецируем это векторной равенство на две взаимно-перпендикулярные оси координат x и y (оси и вектор силы F лежат в одной плоскости) и получим уравнение плоского движения материальной точки в координатной форме:

Применяя теорему о проекции ускорения на координатную ось, эти уравнения можно записать в виде дифференциальных уравнений плоского движения точки:

ΣX = m(d 2 x/dt 2 ) ; ΣY = m(d 2 y/dt 2 ) ,

где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.

С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики :

• по заданному движению точки определяют действующие на нее силы;
• зная действующие на точку силы, определяют ее движение.

В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнении движения наравне с действующими на точку активными силами.

Пример решения первой задачи динамики

Задача: движение тела массой m = 0,5 кг выражается уравнениями:

x = 2t ; y = 3 + t – 5t 2 ,

где x и y (в сантиметрах) – координаты точки в момент времени t (в секундах) .

Определить силу, действующую на тело.

Решение.
Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси x и y :

a_x = d 2 x/dt 2 = 0 ; a_y = d 2 y/dt 2 = — 10 см/с 2 = — 0,1 м/с 2 .

Подставив эти значения в уравнение движения материальной точки, получим:

X = ma_x = 0,5×0 = 0 Н ; Y = ma_y = 0,5×(- 0,1) = — 0,05 Н .

По полученным значениям проекций силы на координатные оси можно сделать вывод, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна:

F = √(X 2 + Y 2 ) = |Y| = 0,05 Н.

Пример решения второй задачи динамики

Задача: на материальную точку массой m = 4 кг , лежащую на гладкой горизонтальной плоскости, действует горизонтальная сила F = 12 Н .
С какой скоростью будет двигаться материальная точка через время t = 10 с , если до приложения силы точка находилась в состоянии покоя?

Решение.
Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F) , запишем уравнение ее движения:

Спроецировав на ось x действующие на точку силы, и подставив в это уравнение значение массы m , определим ускорение точки:

a = ΣX/m = F/m = 12/4 = 3 м/с 2 .

Применим формулу скорости равноускоренного движения и подставим в нее значения, получим:

v = v₀ + at = at = 3×10 = 30 м/с.