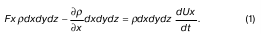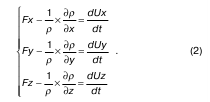Дифференциальные уравнения движения невязкой уравнения эйлера

Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера)

Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера)

Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера). Рассмотрим движущуюся невязкую жидкость плотностью p. выделим основной параллелепипед с ребрами xx, yy и yg, параллельными осям (рис. 4.1). на массу жидкости в объеме параллелепипеда, равную rihuiig, воздействует массовая сила, пропорциональная массе, а на поверхностное давление окружающей жидкости, пропорциональное площади соответствующей поверхности, вдоль внутренних нормалей грани, распределенной вдоль грани parallelepiped.

Если дифференциальная форма уравнений не может быть использована во всем пространстве, заполненном жидкой средой, то используется ее интегральная форма. Людмила Фирмаль

• Построить уравнение движения-рис. 1 Из массы назначенной на проект Разрез по координатным осям. Произведение массы жидкости в параллелепипеде на проекцию ускорения движения центра массы (полюса) в направлении OX равно、 п-ых гг гг йих! У1.、 Здесь они представляют собой скорость центра тяжести в направлении X. Проекция направления OX массовой силы, действующей на массу выделяемой жидкости, равна、 Резус Роге Ю. Г.、 Где Px-проекция плотности распределения массовых сил на ось OX.

Для записи проекции давления на ось OX, в непрерывной жидкой среде, напомним, что давление представляет собой непрерывную функцию P = p (x, y, r, I) с координатами точки жидкости. p обозначает давление любой точки с координатами x, y, r левой вертикальной плоскости. Непрерывность жидкости и непрерывность функции давления делают p = Hx> V> r> 0 справа от точки с координатами (x + yx, y, d) давление равно P+, точность D°dev Конечно, это небольшая второстепенная. Врач. Разница давлений-m-xx одинакова в обоих случаях Бой из 1 набора точек, выбранных в плоскости с одинаковыми координатами y и R.

С другой стороны, проекция результирующего давления на ось OX dh. Да. Я написал уравнение движения для направления OX, поэтому оно выглядит так: Резус Роге Ю. Г. ых Ю. Г.-Ю. Г. Ю. Г. Ю. Роге ЦТ（ Или после деления на массу Рог ый г. ПХ1 др. Р ДХ(11 Аналогично можно получить уравнение движения для проекции направления оси OA и 02. г 1 д-р Йи、 И Г, -=Р ДГ г.（ Диапазон Людмила Фирмаль

• Для жидкостей, которые являются стационарными, их= uy = u2-0 уравнение(4.1) совпадает с дифференциальным уравнением равновесия жидкости (2.4). Уравнение движения невязкой жидкости вдоль обтекаемой поверхности、 п! _ 3& -=, (4.3） 1 п Д1 2> 0 и плотность p (x: y, r, () являются 5 неизвестными функциями. Для определения неизвестных переменных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений, к системе Эйлера добавляются уравнение неразрывности и уравнение состояния среды.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальные уравнения движения невязкой уравнения эйлера

22. Дифференциальные уравнения движения невязкой жидкости

Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.

Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит исходным пунктом для выхода на другие выражения.

Попробуем вывести это уравнение. Пусть имеем бесконечно малый параллелепипед с гранями dxdydz в невязкой жидкости с плотностью ρ. Он заполнен жидкостью и движется как составная часть потока. Какие силы действуют на выделенный объект? Это силы массы и силы поверхностных давлений, которые действуют на dV = dxdydz со стороны жидкости, в которонаходится выделенный dV. Как силы массы пропорциональны массе, так и поверхностные силы пропорциональны площадям, на которые оказывается давление. Эти силы направлены к граням вовнутрь по нормали. Определим математическое выражение этих сил.

Назовем, как и при получении уравнения неразрывности, грани параллелепипеда:

1, 2 – перпендикулярные к оси О_Х и параллельные оси О_Y;

3, 4 – перпендикулярные к оси O_Y и параллельные оси О_Х;

5, 6 – перпендикулярные к оси O_Z и параллельные оси О_Х.

Теперь нужно определить, какая сила приложена к центру масс параллелепипеда.

Сила, приложенная к центру массы параллелепипеда, которая и заставляет эту жидкость совершать движение, есть сумма найденных сил, то есть

Получили уравнение движения параллелепипеда с dV₁ по направлению оси Х.

Делим (1) на массу ρdxdydz:

Полученная система уравнений (2) есть искомое уравнение движения невязкой жидкости – уравнение Эйлера.

К трем уравнениям (2) добавляются еще два уравнения, поскольку неизвестных пять, и решается система из пяти уравнений с пятью неизвестными: одним из двух дополнительных уравнений является уравнение неразрывности. Еще одним уравнением является уравнение состояния. Например, для несжимаемой жидкости уравнением состояния может быть условие ρ = const.

Уравнение состояния должно быть выбрано таким образом, чтобы оно содержало хотя бы одно из пяти неизвестных.

23. Уравнение Эйлера для разных состояний

Уравнение Эйлера для разных состояний имеет разные формы записи. Поскольку само уравнение получено для общего случая, то рассмотрим несколько случаев:

1) движение неустановившееся.

2) жидкость в покое. Следовательно, Ux = Uy = Uz = 0.

В таком случае уравнение Эйлера превращается в уравнение равномерной жидкости. Это уравнение также дифференциальное и является системой из трех уравнений;

3) жидкость невязкая. Для такой жидкости уравнение движения имеет вид

где Fl – проекция плотности распределения сил массы на направление, по которому направлена касательная к линии тока;

dU/dt – ускорение частицы

Подставив U = dl/dt в (2) и учтя, что (∂U/∂l)U = 1/2(∂U 2 /∂l), получим уравнение.

Мы привели три формы уравнения Эйлера для трех частных случаев. Но это не предел. Главное – правильно определить уравнение состояния, которое содержало хотя бы один неизвестный параметр.

Уравнение Эйлера в сочетании с уравнением неразрывности может быть применено для любого случая.

Уравнение состояния в общем виде:

Таким образом, для решения многих гидродинамических задач оказывается достаточно уравнения Эйлера, уравнения неразрывности и уравнения состояния.

С помощью пяти уравнений легко находятся пять неизвестных: p, Ux, Uy, Uz, ρ.

Невязкую жидкость можно описать и другим уравнением

24. Форма Громеки уравнения движения невязкой жидкости

Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.

Например, для координаты x

Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого движения.

Преобразовав точно так же y-вую и z-вую компоненту, окончательно приходим к форме Громеко уравнения Эйлера

Уравнение Эйлера было получено российским ученым Л. Эйлером в 1755 г., и преобразовано в вид (2) опять же российским ученым И. С. Громекой в 1881 г

Уравнение Громеко (под воздействием массовых сил на жидкость):

– dП = Fxdx + Fydy + Fzdz, (4)

то для компонентов Fy, Fz можно вывести те же выражения, что и для Fx, и, подставив это в (2), прийти к (3).

25. Уравнение Бернулли

Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ωx, ωy,ωz угловой скорости w.

Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:

Если теперь сложить

Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:

dx = Uxdt; dy = Uy dt; dz = Uzdt. (3)

Теперь помножим каждое уравнение (3) соответственно на dx, dy, dz, и сложим их:

Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:

Нами получено уравнение Бернулли

26. Анализ уравнения Бернулли

это уравнение есть не что иное, как уравнение линии тока при установившемся движении.

Отсюда следуют выводы:

1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.

2) пропорциональны строки 1 и 2, т. е.

Уравнение (2) является уравнением вихревой линии. Выводы из (2) аналогичны выводам из (1), только линии тока заменяют вихревые линии. Одним словом, в этом случае условие (2) выполняется для вихревых линий;

3) пропорциональны соответствующие члены строк 2 и 3, т. е.

где а – некоторая постоянная величина; если подставить (3) в (2), то получим уравнение линий тока (1), поскольку из (3) следует:

Здесь следует интересный вывод о том, что векторы линейной скорости и угловой скорости сонаправлены, то есть параллельны.

В более широком понимании надо представить себе следующее: так как рассматриваемое движение установившееся, то получается, что частицы жидкости движутся по спирали и их траектории по спирали образуют линии тока. Следовательно, линии тока и траектории частиц – одно и то же. Движение такого рода называют винтовым.

4) вторая строка определителя (точнее, члены второй строки) равна нулю, т. е.

Но отсутствие угловой скорости равносильно отсутствию вихревости движения.

5) пусть строка 3 равна нулю, т. е.

Но это, как нам уже известно, условие равновесия жидкости.

Анализ уравнения Бернулли завершен.

27. Примеры прикладного применения уравнения Бернулли

Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые силы действуют на рассматриваемую жидкость. Поэтому рассмотрим две ситуации.

Одна массовая сила

В этом случае подразумевается сила тяжести, которая выступает в качестве единственной массовой силы. Очевидно, что в этом случае ось Z и плотность распределения Fz силы Ппротивонаправлены, следовательно,

Fx = Fy = 0; Fz = —g.

Поскольку – dП = Fxdx + Fydy + Fzdz, то – dП = Fzdz,окончательно dП = —gdz.

Интегрируем полученное выражение:

где С – некоторая постоянная.

Подставив (1) в уравнение Бернулли, имеем выражение для случая воздействия на жидкость только одной массовой силы:

Если разделить уравнение (2) на g (поскольку оно постоянное), то

Мы получили одну из самых часто применяемых в решении гидравлических задач формул, поэтому следует ее запомнить особенно хорошо.

Если требуется определить расположение частицы в двух разных положениях, то выполняется соотношение для координат Z₁ и Z₂, характеризующие эти положения

Можно переписать (4) в другой форме

28. Случаи, когда массовых сил несколько

В этом случае усложним задачу. Пусть на частицы жидкости действуют следующие силы: сила тяжести; центробежная сила инерции (переносит движение от центра); кориолисовая сила инерции, которая заставляет частицы вращаться вокруг оси Z с одновременным поступательным движением.

В этом случае мы получили возможность представить себе винтовое движение. Вращение происходит с угловой скоростью w. Нужно представить себе криволинейный участок некоторого потока жидкости, на этом участке поток как бы вращается вокруг некоторой оси с угловой скоростью.

Частным случаем такого потока можно считать гидравлическую струю. Вот и рассмотрим элементарную струйку жидкости и применим в отношении к ней уравнение Бернулли. Для этого поместим элементарную гидравлическую струю в координатную систему XYZ таким образом, чтобы плоскость YOX вращалась вокруг оси O_Z.

Будем считать, что U – местная скорость жидкости во вращающейся плоскости YOX. Пусть

составляющие силы тяжести (то есть ее проекции на оси координат), отнесенные к единичной массе жидкости. К этой же массе приложена вторая сила – сила инерции ω 2 r, где r – расстояние от частицы до оси вращения ее компоненты.

из-за того, что ось OZ «не вращается».

Окончательно уравнение Бернулли. Для рассматриваемого случая:

Или, что одно и то же, после деления на g

Если рассмотреть два сечения элементарной струйки, то, применив вышеуказанный механизм, легко убедиться, что

Дифференциальные уравнения движения невязкой уравнения эйлера

22. Дифференциальные уравнения движения невязкой жидкости

Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.

Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит исходным пунктом для выхода на другие выражения.

Попробуем вывести это уравнение. Пусть имеем бесконечно малый параллелепипед с гранями dxdydz в невязкой жидкости с плотностью ?. Он заполнен жидкостью и движется как составная часть потока. Какие силы действуют на выделенный объект? Это силы массы и силы поверхностных давлений, которые действуют на dV = dxdydz со стороны жидкости, в которонаходится выделенный dV. Как силы массы пропорциональны массе, так и поверхностные силы пропорциональны площадям, на которые оказывается давление. Эти силы направлены к граням вовнутрь по нормали. Определим математическое выражение этих сил.

Назовем, как и при получении уравнения неразрывности, грани параллелепипеда:

1, 2 – перпендикулярные к оси О_Х и параллельные оси О_Y;

3, 4 – перпендикулярные к оси O_Y и параллельные оси О_Х;

5, 6 – перпендикулярные к оси O_Z и параллельные оси О_Х.

Теперь нужно определить, какая сила приложена к центру масс параллелепипеда.

Сила, приложенная к центру массы параллелепипеда, которая и заставляет эту жидкость совершать движение, есть сумма найденных сил, то есть

Получили уравнение движения параллелепипеда с dV₁ по направлению оси Х.

Делим (1) на массу ?dxdydz:

Полученная система уравнений (2) есть искомое уравнение движения невязкой жидкости – уравнение Эйлера.

К трем уравнениям (2) добавляются еще два уравнения, поскольку неизвестных пять, и решается система из пяти уравнений с пятью неизвестными: одним из двух дополнительных уравнений является уравнение неразрывности. Еще одним уравнением является уравнение состояния. Например, для несжимаемой жидкости уравнением состояния может быть условие ? = const.

Уравнение состояния должно быть выбрано таким образом, чтобы оно содержало хотя бы одно из пяти неизвестных.