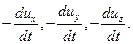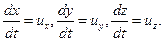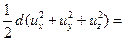Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера)



Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера)
Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера). Рассмотрим движущуюся невязкую жидкость плотностью p. выделим основной параллелепипед с ребрами xx, yy и yg, параллельными осям (рис. 4.1). на массу жидкости в объеме параллелепипеда, равную rihuiig, воздействует массовая сила, пропорциональная массе, а на поверхностное давление окружающей жидкости, пропорциональное площади соответствующей поверхности, вдоль внутренних нормалей грани, распределенной вдоль грани parallelepiped.
Если дифференциальная форма уравнений не может быть использована во всем пространстве, заполненном жидкой средой, то используется ее интегральная форма. Людмила Фирмаль
- Построить уравнение движения-рис. 1 Из массы назначенной на проект Разрез по координатным осям. Произведение массы жидкости в параллелепипеде на проекцию ускорения движения центра массы (полюса) в направлении OX равно、 п-ых гг гг йих! У1.、 Здесь они представляют собой скорость центра тяжести в направлении X. Проекция направления OX массовой силы, действующей на массу выделяемой жидкости, равна、 Резус Роге Ю. Г.、 Где Px-проекция плотности распределения массовых сил на ось OX.
Для записи проекции давления на ось OX, в непрерывной жидкой среде, напомним, что давление представляет собой непрерывную функцию P = p (x, y, r, I) с координатами точки жидкости. p обозначает давление любой точки с координатами x, y, r левой вертикальной плоскости. Непрерывность жидкости и непрерывность функции давления делают p = Hx> V> r> 0 справа от точки с координатами (x + yx, y, d) давление равно P+, точность D°dev Конечно, это небольшая второстепенная. Врач. Разница давлений-m-xx одинакова в обоих случаях Бой из 1 набора точек, выбранных в плоскости с одинаковыми координатами y и R.
- С другой стороны, проекция результирующего давления на ось OX dh. Да. Я написал уравнение движения для направления OX, поэтому оно выглядит так: Резус Роге Ю. Г. ых Ю. Г.-Ю. Г. Ю. Г. Ю. Роге ЦТ( Или после деления на массу Рог ый г. ПХ1 др. Р ДХ(11 Аналогично можно получить уравнение движения для проекции направления оси OA и 02. г 1 д-р Йи、 И Г, -=Р ДГ г.( Диапазон Людмила Фирмаль
- Для жидкостей, которые являются стационарными, их= uy = u2-0 уравнение(4.1) совпадает с дифференциальным уравнением равновесия жидкости (2.4). Уравнение движения невязкой жидкости вдоль обтекаемой поверхности、 п! _ 3& -=, (4.3) 1 п Д1 2> 0 и плотность p (x: y, r, () являются 5 неизвестными функциями. Для определения неизвестных переменных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений, к системе Эйлера добавляются уравнение неразрывности и уравнение состояния среды.
Смотрите также:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Основные дифференциальные уравнения движения невязкой жидкости
Страницы работы
Содержание работы

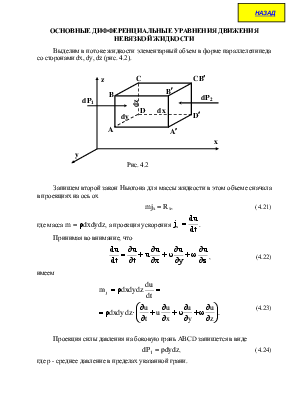
Выделим в потоке жидкости элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (рис. 4.2).
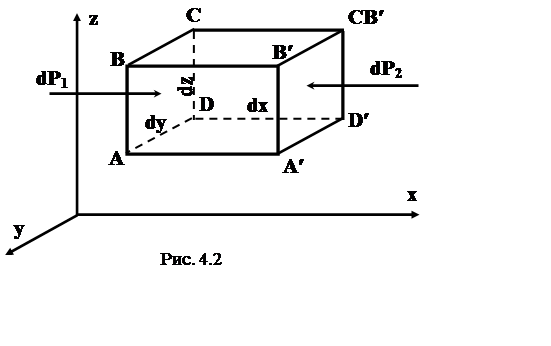 |
Запишем второй закон Ньютона для массы жидкости в этом объеме сначала в проекциях на ось ох
где масса m = rdxdydz, а проекция ускорения 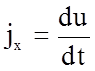
Принимая во внимание, что
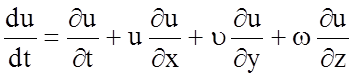
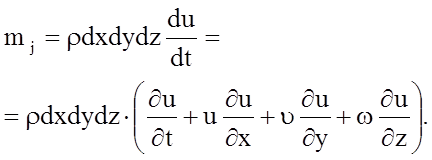
Проекция силы давления на боковую грань АВСD запишется в виде
где p — среднее давление в пределах указанной грани.

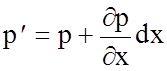
и, следовательно, сила давления на эту грань
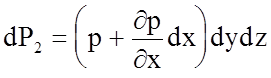
Сумма проекций поверхностных сил на боковые грани
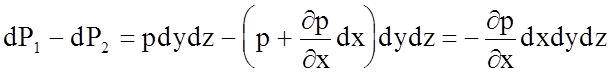
Проекцию объемных сил Fx на ось ох можно записать в виде
Тогда, с учетом вышеизложенного, имеем:
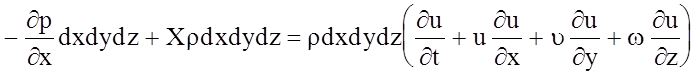
Относя к единице массы (сокращая на r×dxdydz) получим:
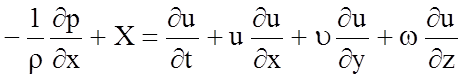
Аналогичные результаты получаются и для других осей.
В результате получаем следующую систему уравнений.
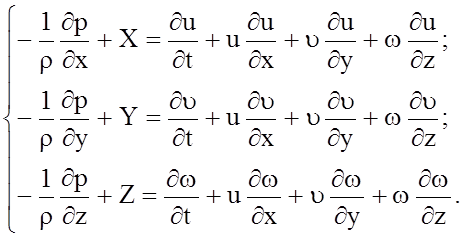

В систему из 3-х уравнений входят пять неизвестных функций:
Вследствие этого, для возможности решения системы, ее необходимо дополнить еще двумя уравнениями: сплошности и состояния.
Дифференциальное уравнение движения невязкой жидкости (уравнение Эйлера)
Предположим, что в жидкости движется элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (см. рис. 2.38). На параллелепипед действуют поверхностные силы давления и массовые силы с проекциями X, Y, Z, отнесенными к единице массы. При движении объема возникают силы инерции. Проекции этих сил на оси координат, отнесенные к единице массы, равны соответственно:
Рис. 2.38. Схема равномерного движения объема жидкости
Рассмотрим условие равновесия сил, в проекции на ось х. Сила давления на левую грань – pdydz, на правую грань
–(p + 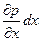
где 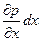
Массовая сила равна Xρdxdydz. Уравнение равновесия запишется в виде
pdydz – (p + 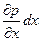
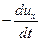
– 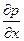
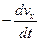
Разделив каждый член уравнения на ρdxdydz, получим
X – 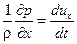
Соответственно для осей и уравнение равновесия будет выглядеть следующим образом
Y – 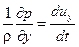
Z – 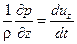
Объединив полученные уравнения, получим систему уравнений Эйлера:
X – 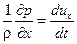
Y – 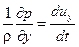 , , | (2.42) |
Z – 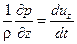
Можно получить полный дифференциал уравнений Эйлера для установившегося движения, если рассматривать перемещение частиц жидкости вдоль линии тока. Для этого надо умножить каждое из уравнений системы на соответствующую проекцию элементарного перемещения частиц dx, dy, dz, и сложить их:
(Xdx + Ydy + Zdz) – 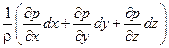
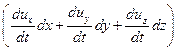
Т.к. для установившегося течения линии тока совпадают с траекториями движения частиц, то
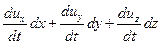
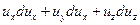
Для установившегося движения давление зависит только от координат, поэтому второй член уравнения есть полный дифференциал давления dp. Получим
(Xdx + Ydy + Zdz) – 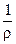 dp – dp – 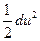 = 0 = 0 | (2.43) |
Мы получили дифференциальное уравнение движения невязкой жидкости.
В поле силы тяжести
тогда уравнение запишется в следующем виде
– gdz – 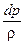
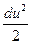
После интегрирования этого уравнения получаем (при ρ = const) уравнение
gz + 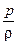 + + 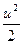 = const, = const, | (2.44) |
которое называется уравнением Бернулли для струйки невязкой жидкости.
2.2.6. Общее уравнение энергии в интегральной форме
(Уравнение Бернулли для потока реальной жидкости)
Для двух сечений струйки невязкой жидкости это уравнение будет выглядеть следующим образом
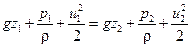 . . | (2.45) |
Сумма слева представляет полную удельную энергию струйки в сечении 1-1, сумма справа – полную удельную энергию струйки в сечении 2-2. Можно записать, что
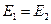
На практике энергия струйки в начале больше энергии струйки в конце, т.к. часть энергии теряется на преодолении сил вязкости. В процессе движения вязкой жидкости запас ее механической энергии уменьшается, и на самом деле
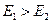
Обозначим энергию, затрачиваемую на преодоление сил сопротивления Eпот. Eпот – это та часть механической энергии, которая, вследствие вязкости, переходит в тепловую энергию. Другими словами можно сказать, что Eпот – это часть энергии, которая израсходована на преодоление гидравлических сопротивлений.
| Е1 = Е2 + Eпот. | (2.46) |
При выводе уравнения Бернулли для элементарной струйки можно было пренебречь изменением скорости и давления в пределах нормальных сечений благодаря их малым величинам. В потоке жидкости скорости и давления в пределах живых сечений различны, и это необходимо учитывать. Согласно гипотезе Ньютона, жидкость как бы прилипает к стенкам канала, по которому она течет и ее скорость равна нулю. Но с увеличением расстояния от стенки, скорость струек увеличивается. Так называемая мощность потока складывается из энергии отдельных струек
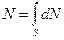
где N – мощность потока; dN – мощность струйки; S – площадь живого сечения потока.
Для мощности струйки можно записать:
dN = Ed 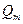
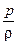
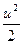
где ds – площадь живого сечения струйки.
Величина удельной энергии потока равна частному от деления мощности потока на массовый расход
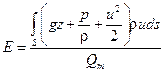
Это уравнение можно разбить на два интеграла
E = 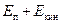


где 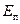
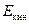
Для вычисления 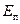
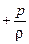
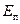 = = 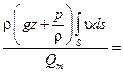 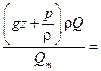 gz gz 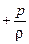 . . | (2.47) |
Для вычисления интеграла 


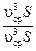
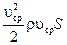
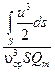
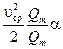
где α – коэффициент, который учитывает неравномерность распределения скоростей в сечении, называется коэффициент Кориолиса. Получаем выражение для удельной кинетической энергии потока:
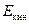 = = 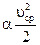 . . | (2.48) |
Запишем уравнение Бернулли для двух сечений потока реальной жидкости
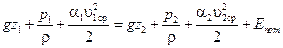 . . | (2.49) |
Полученное уравнение позволяет сделать следующие выводы:
1. При увеличении кинетической энергии потока от одного сечения к другому потенциальная энергия уменьшается, и, наоборот, с увеличением потенциальной энергии, кинетическая уменьшается.
2. Коэффициент α тем больше, чем больше скорости отдельных струек отличаются от величины средней скорости. Если скорости всех элементарных струек будут равны средней скорости, то α = 1.
http://vunivere.ru/work49566
http://helpiks.org/4-108757.html