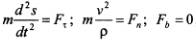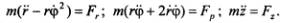Дифференциальные уравнения движения точки две задачи динамики точки

Две основные задачи динамики точки. Интегралы дифференциальных уравнений движения.

Две основные задачи динамики точки:

1. Первая задача состоит в том, чтобы по заданному закону движения точки массой m определить силу, под действием которой происходит это движение. Часто первую задачу рассматривают как задачу управления движением, в рамках которой требуется установить характеристики воздействия, обеспечивающие заданный закон движения материальной точки. В зависимости от способа задания движения при решении этой задачи используют соответствующие скалярные уравнения.

(13.3)

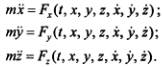
2. Вторая задача состоит в определении движения точки по заданным силам и начальным условиям движения, при этом силы должны быть выражены как функции переменных, используемых для задания движения. Решение этой задачи сводится к интегрированию дифференциальных уравнений второго порядка, в процессе которого в решениях появляются произвольные постоянные, подлежащие определению. 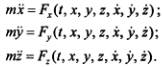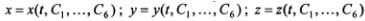Так, в задаче о движении точки в трехмерном пространстве, решаемой на основе дифференциальных уравнений , общие решения будут содержать шесть произвольных постоянных:

для определения которых потребуется постановка дополнительных условий. Из математики известно, что если эти условия поставлены для начальных (при t = 0) значений функций и их первых производных, т. е. в виде x(0)=х₀, y(0)=у₀, z(0)=z₀, 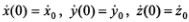,то задача (задача Коши) при некоторых ограничениях, налагаемых на правые части дифференциальных уравнений, имеет решение и причем единственное. Таким образом, приложенные к точке силы определяют только ее ускорение, движение же точки помимо сил зависит от начальных условий — положения точки в рассматриваемой инерциальной системе отсчета и ее скорости.

Две основные задачи динамики точки (из лекций):

1. Прямая: Зная m и действующую силу, определим движение материальной точки.

2. Обратная: Зная m материальной точки и ее уравнение движения, можно найти действующую на точку силу.

Интегралы дифференциальных уравнений движения.

Техническая механика

Динамика

Принцип независимости действия сил

Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности .

Пусть к материальной точке А приложены силы F₁ и F₂ равнодействующая которых равна F на основании аксиомы параллелограмма запишем:

Разделив обе части равенства на массу точки m , получим:

Применяя последовательно аксиому параллелограмма, можно показать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила F = ΣF_i .

Пользуясь изложенным выше принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.

Дифференциальные уравнения движения материальной точки

Пусть материальная точка А массой m движется в плоскости чертежа под действием равнодействующей силы F = ΣF_i с ускорением а , тогда:

Спроецируем это векторной равенство на две взаимно-перпендикулярные оси координат x и y (оси и вектор силы F лежат в одной плоскости) и получим уравнение плоского движения материальной точки в координатной форме:

Применяя теорему о проекции ускорения на координатную ось, эти уравнения можно записать в виде дифференциальных уравнений плоского движения точки:

ΣX = m(d 2 x/dt 2 ) ; ΣY = m(d 2 y/dt 2 ) ,

где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.

С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики :

по заданному движению точки определяют действующие на нее силы;
зная действующие на точку силы, определяют ее движение.

В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнении движения наравне с действующими на точку активными силами.

Пример решения первой задачи динамики

Задача: движение тела массой m = 0,5 кг выражается уравнениями:

x = 2t ; y = 3 + t – 5t 2 ,

где x и y (в сантиметрах) – координаты точки в момент времени t (в секундах) .

Определить силу, действующую на тело.

Решение.
Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси x и y :

a_x = d 2 x/dt 2 = 0 ; a_y = d 2 y/dt 2 = — 10 см/с 2 = — 0,1 м/с 2 .

Подставив эти значения в уравнение движения материальной точки, получим:

X = ma_x = 0,5×0 = 0 Н ; Y = ma_y = 0,5×(- 0,1) = — 0,05 Н .

По полученным значениям проекций силы на координатные оси можно сделать вывод, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна:

F = √(X 2 + Y 2 ) = |Y| = 0,05 Н.

Пример решения второй задачи динамики

Задача: на материальную точку массой m = 4 кг , лежащую на гладкой горизонтальной плоскости, действует горизонтальная сила F = 12 Н .
С какой скоростью будет двигаться материальная точка через время t = 10 с , если до приложения силы точка находилась в состоянии покоя?

Решение.
Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F) , запишем уравнение ее движения:

Спроецировав на ось x действующие на точку силы, и подставив в это уравнение значение массы m , определим ускорение точки:

a = ΣX/m = F/m = 12/4 = 3 м/с 2 .

Применим формулу скорости равноускоренного движения и подставим в нее значения, получим:

v = v₀ + at = at = 3×10 = 30 м/с.

Две основные задачи динамики точки

Используя дифференциальное уравнение движения массы в конкретной системе координат, вы можете решить две основные задачи с точечной динамикой. Первое задание Зная массу точки и законы ее движения, вы сможете найти силу, действующую на точку. Фактически, например, дано уравнение движения декартовой координатной точки Далее проекция силы на оси координат определяется из дифференциального уравнения движения точки (9). Е

сли вам известна проекция силы на координатную ось, вы можете легко определить модуль упругости силы, угол силы и косинус координатной оси. Пример I. Точка М. Их Ohu — это уравнение Где a, b, k — постоянные положительные ве- Точка определяет силу, чтобы сделать это движение. Решения. Найти точечное уравнение траектории в координатной форме, исключив время из уравнения движения. самолет Рисунок 5 i + 3’2 / fr2 = cos2fct + sin2fcr = l. Полуэллипс Пример 2. Точка / / с массой m (рис. 6) движется из стационарного состояния по окружности радиуса с с постоянным тангенциальным ускорением a.

Когда все силы инерции точек системы исчезают по принципу возможного смещения статики, только в случае равновесия системы, до сих пор нет проблем с устойчивостью системы. Людмила Фирмаль

Определить силу, действующую на точку в момент, соответствующий орбитальному расстоянию s = Ry / l. Дифференциальное уравнение движения точки на профессиональной естественной оси. У нас есть: ускорение Идти вниз Kings s = Ry / 2 = att2l2, a, t2IR = 2y / 2, так что? / 4 / Я2 = 8 моментов Касательная угла a между радиусом окружности и силой I Рассматривая первую проблему точечной динамики, мы видим, что сила полностью определяется как по величине, так и по направлению в соответствии с заданной массой точки и ее уравнением движения.

Второе задание Учитывая массу и силу, действующую на точку, нам нужно определить движение этой точки. Рассмотрим решение этой проблемы в декартовой декартовой системе координат. В общем случае сила F и, следовательно, проекция на оси могут зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. Д. Для простоты мы ограничимся зависимостью силы и ее оси. Проекция на координатные оси времени, координат и скорости. Форма дифференциального уравнения для движения точки (9) имеет вид ”* ■ r- * ■> ‘■ * • Y— • * •>’ • d); (9 ‘) Чтобы найти уравнение движения точки в декартовых координатах, нам нужно интегрировать систему из трех обыкновенных дифференциальных уравнений второго порядка.

Теория обыкновенных дифференциальных уравнений показывает, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для системы из трех обыкновенных дифференциальных уравнений второго порядка существует шесть произвольных постоянных: постоянная C C2, C3, C4, C5, C6. Координаты x, y, z движущейся точки после интегрирования уравнений уравнения (9) зависят от времени t и всех шести произвольных постоянных. x = f1 (t; Cl, C2, C3, C4, Cs, C6 \ -y y = fz (t, C3, C2, C3, C4, C5, C6);> (13) 2 = / s (/; c2, c2, c3, sl, c5, c6) .

Дифференцирующее уравнение (13) по времени определяет проекцию скорости точек на оси. vx = x = f’t (f, Ct, C2, C3, C4, C5, C6);) ^ = j = / ‘2 (CG, C2, C3, C4, C5, C6); (14) yy = y = D (f; C „Cr, C3, C4, C5, C6). J Таким образом, силовое задание не определяет специфическое движение массы, но выделяет весь класс движения, характеризуемый шестью произвольными константами. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории зависят от скорости, передаваемой в точку в начальный момент, и начальной позиции точки.

Так, например, когда сопротивление воздуха не учитывается, точка вещества, которая движется вблизи поверхности земли под действием силы тяжести, имеет ускорение g. Тем не менее, точки имеют разные скорости и положения в пространстве в один и тот же момент, в зависимости от точки в пространстве, где началось движение, величины и направления начальной скорости, а также формы траектории. Чтобы подчеркнуть определенный тип движения массы, вам нужно установить дополнительные условия, которые могут определить любую константу.

Это вообще 6. Такие условия обычно задаются как Вызывается начальные условия, то есть определенный момент времени, например I = 0 (рис. 7), координаты движущейся точки x0, y0, z0 и ее скорости vOx, проекция, t> Z * 7) (| 5) * = «О; у =» 0). ; Z = воз-J Рисунок 7 Использование этих начальных условий Используйте уравнения и (13) и (14), чтобы получить следующие шесть уравнений, чтобы определить шесть произвольных постоянных. * o = / 1 (0; c15 C2, C3, C4, Cs, C6); Y0 = / 2 (0; C1, C2, C3, Cl, C5, C6); zo = / 3 <0; G, C2 , C3, C4, C5, C6) vOx ^ f’i (0; citc2, …, wYy = A (0; C „C2, …. C6); »O, — / s (0; c„ c2, …, c6). (16).

Поэтому система отсчета, в которой материальная точка покоится, должна иметь соответствующую систему отсчета для материальной точки, поскольку относительная скорость и ускорение равны нулю. Людмила Фирмаль

Если система уравнений (16) удовлетворяет условию разрешимости, из него можно определить все шесть произвольных постоянных. Начальное условие вида (15) определяет единственное решение системы дифференциальных уравнений (9) при условии соответствующего условия дифференциального уравнения. Другие формы условий, такие как указание двух точек, через которые должна проходить траектория движущейся точки, могут предоставить несколько решений, которые удовлетворяют этим условиям, или не могут найти единого решения.

Когда точка движется в плоскости Оху, существуют два дифференциальных уравнения движения. Решение этих уравнений включает в себя четыре произвольные постоянные. Константа определяется из начальных условий r равно 0. x = x0; y = y0; x = Vox; j> = »или Для линейного движения точки существует только одно дифференциальное уравнение, и решение содержит две произвольные постоянные. Чтобы определить их, необходимо установить начальные условия. r равно 0. x = x0; x = vOx. Задача интегрирования системы дифференциальных уравнений (9 ‘) при заданных начальных условиях в общем случае достаточно сложна.

Даже в простейшем случае Если существует только одно линейное движение или дифференциальное уравнение, решение может быть точно выражено квадратурой только в том случае, если сила имеет конкретную зависимость от времени r, координаты x и скорости v. Поэтому важно определить такое соотношение из системы уравнений (9 ‘), которая является результатом этой системы и содержит производную от координат точки первого порядка. Такое отношение, например, в виде / p; x, y, z; x, y, z).

C называется первым интегралом системы дифференциальных уравнений (9 ‘) -системой (9’) Задача интегрирования упрощается, если можно найти три независимых первых интеграла. Три дифференциальных уравнения первого порядка, представленные этими первыми интегралами. Далее из так называемой общей теоремы динамики в некоторых частных случаях движения точки мы рассмотрим, как получить первый интеграл дифференциального уравнения движения точки. Чтобы уточнить характеристики решения, которое применяет значение, второй основной проблемы динамики, мы рассмотрим решения для линейных и изогнутых движений массы.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://k-a-t.ru/tex_mex/22-dinamika_2/index.shtml

http://lfirmal.com/dve-osnovnye-zadachi-dinamiki-tochki/