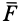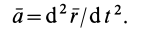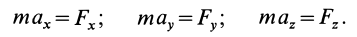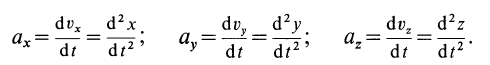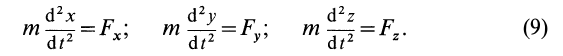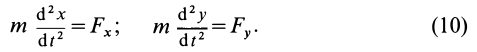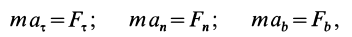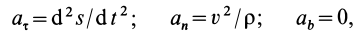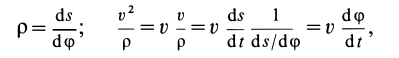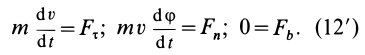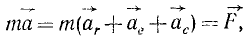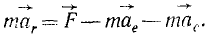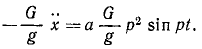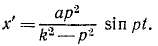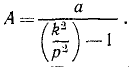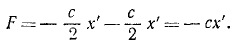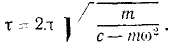Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
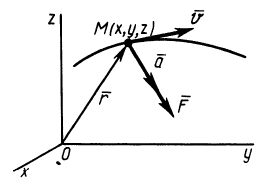
Из кинематики точки известно, что ускорение 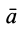
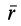
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 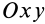
Так как 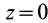
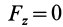
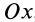
Так как при движении 
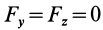
где 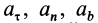
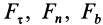
где 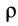
Второе уравнение из (12) можно преобразовать:
где 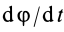
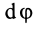
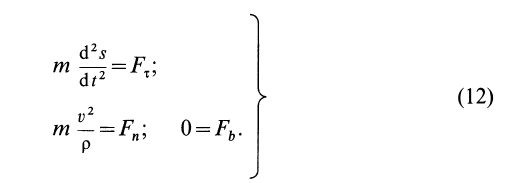
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 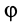
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
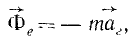
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
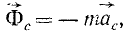
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
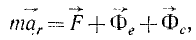
или в проекциях на оси координат:
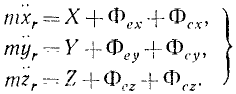
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
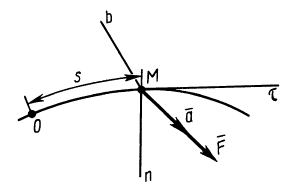
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
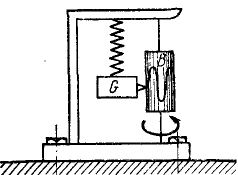
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 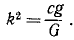
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 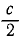
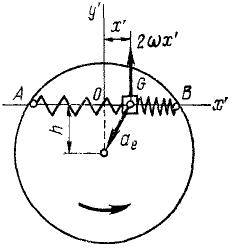
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 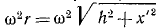
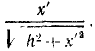
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 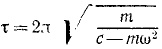
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Техническая механика
Динамика
Принцип независимости действия сил
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности .
Пусть к материальной точке А приложены силы F1 и F2 равнодействующая которых равна F на основании аксиомы параллелограмма запишем:
Разделив обе части равенства на массу точки m , получим:
Применяя последовательно аксиому параллелограмма, можно показать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила F = ΣFi .
Пользуясь изложенным выше принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.
Дифференциальные уравнения движения материальной точки
Пусть материальная точка А массой m движется в плоскости чертежа под действием равнодействующей силы F = ΣFi с ускорением а , тогда:
Спроецируем это векторной равенство на две взаимно-перпендикулярные оси координат x и y (оси и вектор силы F лежат в одной плоскости) и получим уравнение плоского движения материальной точки в координатной форме:
Применяя теорему о проекции ускорения на координатную ось, эти уравнения можно записать в виде дифференциальных уравнений плоского движения точки:
ΣX = m(d 2 x/dt 2 ) ; ΣY = m(d 2 y/dt 2 ) ,
где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.
С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики :
- по заданному движению точки определяют действующие на нее силы;
- зная действующие на точку силы, определяют ее движение.
В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнении движения наравне с действующими на точку активными силами.
Пример решения первой задачи динамики
Задача: движение тела массой m = 0,5 кг выражается уравнениями:
x = 2t ; y = 3 + t – 5t 2 ,
где x и y (в сантиметрах) – координаты точки в момент времени t (в секундах) .
Определить силу, действующую на тело.
Решение.
Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси x и y :
ax = d 2 x/dt 2 = 0 ; ay = d 2 y/dt 2 = — 10 см/с 2 = — 0,1 м/с 2 .
Подставив эти значения в уравнение движения материальной точки, получим:
X = max = 0,5×0 = 0 Н ; Y = may = 0,5×(- 0,1) = — 0,05 Н .
По полученным значениям проекций силы на координатные оси можно сделать вывод, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна:
F = √(X 2 + Y 2 ) = |Y| = 0,05 Н.
Пример решения второй задачи динамики
Задача: на материальную точку массой m = 4 кг , лежащую на гладкой горизонтальной плоскости, действует горизонтальная сила F = 12 Н .
С какой скоростью будет двигаться материальная точка через время t = 10 с , если до приложения силы точка находилась в состоянии покоя?
Решение.
Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F) , запишем уравнение ее движения:
Спроецировав на ось x действующие на точку силы, и подставив в это уравнение значение массы m , определим ускорение точки:
a = ΣX/m = F/m = 12/4 = 3 м/с 2 .
Применим формулу скорости равноускоренного движения и подставим в нее значения, получим:
v = v0 + at = at = 3×10 = 30 м/с.
Дифференциальные уравнения движения материальной точки



Дифференциальные уравнения движения материальной точки
- Используя фундаментальные законы динамики, вы можете вывести дифференциальные уравнения для движения точек массы в различных системах координат. Используя аксиомы ограничений и силу связанных реакций, вы можете получить дифференциальные уравнения движения и несвободные точки так же, как свободные уравнения. Только сила объединенной реакции должна быть добавлена к каждой силе, приложенной к точке.
Сила реакции связи во время движения точки — это не только тип связи, приложенной к точке и приложенной к ней силы, но также характер движения, например, перемещение в воздухе или другой резистивной среде. Это также зависит от скорости, когда вы делаете. В будущем мы не будем различать свободные и несвободные материальные точки. Приведены результаты всех приведенных сил и объединенной силы реакции F, а также массы точки m, ма ^ F. (7) Из кинематики точек видно, что ускорение a выражается радиус-вектором g (рис. 3). a = d2r / dt2.
Регулятор представляет собой устройство, предназначенное для приведения изменений средней скорости машины, вызванных изменением движущей силы или силы сопротивления, как можно ближе друг к другу. Людмила Фирмаль
Форма дифференциального уравнения движения точки массы в векторной форме имеет вид Спроецируйте обе части уравнения (7) или (8) на оси координат, чтобы получить производную Уравнение движения точек в проекциях на эти оси. Декартова система координат для общего случая max-Fx; ma, -Fy; maz-fx. Проекция ускорения на оси координат может быть выражена как вторая производная по времени от координат движущейся точки. Рисунок 3 _d »r_d2T. _dt>. _d2z y df d / 2 ′ 1 dt d / 2 ‘ Дифференциальное уравнение движения массы в декартовой декартовой системе координат имеет вид улица Особый случай. Если вы знаете, что точка массы движется в одной плоскости, возьмите ее в координатную плоскость Оху, (U) Поскольку z = 0, значит, Fz = 0.
- Если точка движется по прямой и ориентирует оси Ox вдоль нее, вы получите одно дифференциальное уравнение для линейного движения точки. (А) Поскольку движение y = z = 0, то Fy = Fz = 0. Для естественной движущейся координатной оси (рисунок 4), которая проецирует обе части (7) на эти оси, вы получаете: maz = Ft; ma „= F„; mab = Fb, Где a, a „, ab и Fz, F„, Fb — это проекции ускорения и результирующей силы на касательную, основную нормаль и субнормаль траектории в рассматриваемом положении точки движения, соответственно.
Учитывая, что az = d2s / dt2; a „= v2 / p; ab = 0, Где p — радиус кривизны траектории, а дифференциальное уравнение для движения спроецированной точки по естественной оси m- = F „; 0 = Fb. р Второе уравнение из (12) можно преобразовать. дс в2 в дс я дтп p = -: — = v-— v ——-— v
, дтп п р дтдс / дтп дт Где d
В свою очередь колебательное движение механической системы в целом имеет колебательный характер, то есть не все обобщенные координаты или некоторые из них изменяются монотонно. Людмила Фирмаль
Эта форма дифференциального уравнения движения точки полезна Некоторые тематические исследования — рисунок 4 В частности, снаряд и ракета летят по плоской орбите. Затем
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://k-a-t.ru/tex_mex/22-dinamika_2/index.shtml
http://lfirmal.com/differencialnye-uravneniya-dvizheniya-materialnoj-tochki/