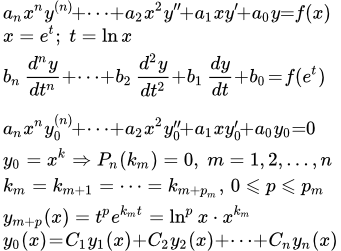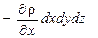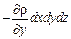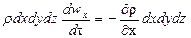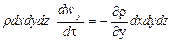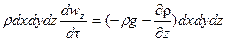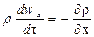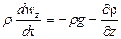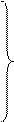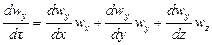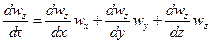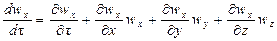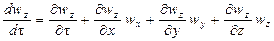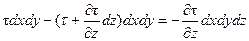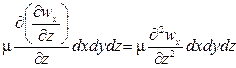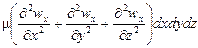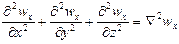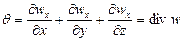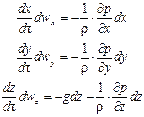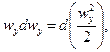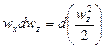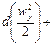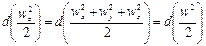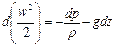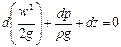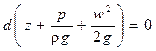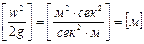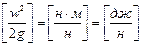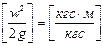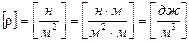Дифференциальное уравнение Эйлера и методы его решения
Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Дифференциальные уравнения движения Эйлера
Рассмотрим установившийся поток идеальной жидкости. Как уже говорилось, она не обладает вязкостью, т.е. движется без трения.
Как и при выводе дифференциальных уравнений равновесия Эйлера, выделим в потоке элементарный параллелепипед объемом dV = dxdydz, ориентированный относительно осей координат (см. рис. II-2).
Проекции на оси координат сил тяжести и давления, действующих на параллелепипед, составляют;
для оси х:
для оси у:
для оси z: 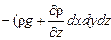
Согласно основному принципу динамики, сумма проекций сил, дейcтвующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.
Масса жидкости в объеме параллелепипеда
Если жидкость движется со скоростью ли, то ее ускорение равно w, то проекции ускорения на оси координат: 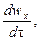
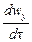
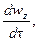
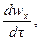
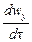
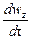
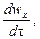
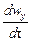
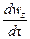
В соответствии с основным принципом динамики
или после сокращения
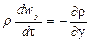
где, согласно уравнению (II,28а), субстанциональные производные соответствующих составляющих скорости равны
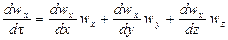
Система уравнений (II,46) с учетом выражений (II,47) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлерадля установившегося потока.
При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке. Поэтому, в соответствии с уравнением (II,28), составляющие ускорения в уравнении (II,46), выражаемые субстанциональными производными для неустановившихся условий, имеют вид:
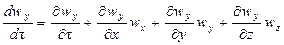
Система уравнений (II,46) с учетом выражений (II,47а) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.
Интегралом уравнений движения Эйлера для установившегося потока является уравнение Бернулли, широко используемое для решения многих технических задач.
4. Дифференциальные уравнения движения Навье-Стокса
При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.
Действие сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед (рис. II-14) проявляется в возникновении на его поверхности касательных напряжений t.
Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости wx зависит только от расстояния r до горизонтальной плоскости отсчета.
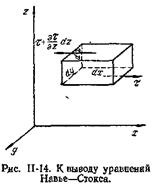

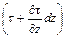
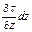
Указанные на рис. II-14 стрелками направления сил трения, приложенных к параллелепипеду на его нижней и верхней гранях, обусловлены, например, тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его.
Тогда проекция равнодействующей сил трения на ось х
Подставив в это выражение значение касательного напряжения t по уравнению (II,12а) [t = 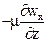
В более общем случае трехмерного потока составляющая скорости wx будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось x примет вид
Сумму вторых производных по осям координат называют оператором Лапласа:
Следовательно, проекция равнодействующей сил трения на ось х может быть представлена как m 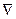
Соответственно проекции равнодействующей сил трения:
на ось у: m 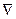
на ось z: m 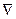
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:
на ось х: ( 
на ось у: ( 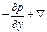
на ось z: ( 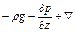
Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости rdxdydz (r — плотность жидкости), заключенной в элементарном объеме, на проекции ускорения на оси координат. Поэтому, приравнивая проекции равнодействующей произведениям массы на проекции ускорения, после сокращения на dxdydz, получим
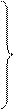
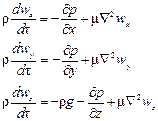
где соответствующие субстанциональные производные выражены для установившегося и неустановившегося потоков уравнениями (II,47) или (II,47а).
Уравнения (II,48) представляют собой уравнения Навье-Cтокса, описывающие движение вязкой капельной жидкости.
При движении сжимаемой жидкости (газа) в ней дополнительно возникают вызванные трением силы сжатия и растяжения, поэтому уравнения Навье-Стокса принимают вид:
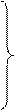
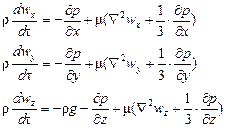
где частные производные 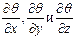
Левые части уравнений (II,48) выражают произведение массы единицы объема r на проекцию ее ускорения, т.е. представляют собой проекции равнодействующей сил инерции, возникающих в движущейся жидкости.
В правых частях тех же уравнений произведение pg отражает влияние сил тяжести, частные производные 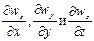
Каждый член уравнений (II,48) имеет размерность соответствующей силы (тяжести, давления, трения или инерции), отнесенной к единице объема жидкости.
При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке m = 0 в уравнения (II,48) последние совпадают с уравнениями (II,46), т.е. уравнения движения Эйлера можно получить как частный случай уравнений Навье-Стокса.
Полное описание движения вязкой жидкости в его наиболее общей форме возможно путем решения уравнений Навье-Стокса совместно с уравнением неразрывности потока. Однако уравнения Навье-Стокса не могут быть решены в общем виде. Получены решения этой сложной системы уравнений только для некоторых частных случаев. Так, для установившегося ламинарного движения жидкости решение уравнений Навье-Cтокса позволяет вывести уравнение Пуазейля, полученное выше другим способом.
В большинстве же наиболее важных для промышленной практики случаев применение уравнений Навье-Стокса становится возможным либо при ряде упрощающих допущений, либо при преобразовании этих сравнений методами теории подобия.
5. Уравнение Бернулли
Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики — уравнению Бернулли.
Умножив левые и правые части каждого из уравнений (II,46) соответственно на dx, dy и dz и разделив на плотность р жидкости, получим
Сложим эти уравнения, учитывая, что производные 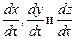
Слагаемые левой части этого уравнения могут быть представлены как
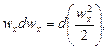
следовательно, их сумма
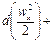
где w = 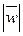
В то же время сумма членов, стоящих в скобках в правой части записанного уравнения, представляет собой полный дифференциал давления dp (при установившихся условиях давление зависит лишь от положения точки в пространстве, но в каждой данной точке не меняется со временем). Значит
Разделив обе части этого уравнения на ускорение свободного падения g и перенеся все его члены в левую часть, находим
причем для несжимаемой однородной жидкости r = const.
Сумма дифференциалов может быть заменена дифференциалом суммы, следовательно
Уравнение (II,49) для любых двух поперечных сечений 1 и 2 потока (трубопровода) можно представить в виде
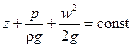
Уравнение (II,49) является уравнением Бернулли для идеальной жидкости.
Величину 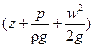
Следовательно, согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости гидродинамический напор остается неизменным.
Гидродинамический напор включает три слагаемых, из которых первые два слагаемых, z и 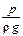
z — нивелирная высота, называемая также геометрическим, или высотным, напором (hг), представляет собой удельную потенциальную энергию положения в данной точке (данном сечении);
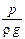
Сумма z+ 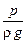
Величины z и 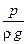
Третья составляющая, 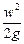
или после умножения и деления на единицу веса (н — в СИ или кгс – в системе МКГСС)
Величину называют скоростным, или динамическим напором и обозначают через hck. Скоростной напор характеризует удельную кинетическую энергию в данной точке (данном сечении).
Таким образом, согласно уравнению Бернулли, при установившемся движении идеальной жидкости сумма скоростного и статического напоров, равная гидродинамическому напору, не меняется при переходе от одного поперечного сечения потока к другому.
Вместе с тем из уравнения Бернулли в соответствии с энергетическим смыслом его членов следует, что при установившемся движении идеальной жидкости сумма потенциальной (z + 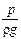
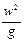
При изменении поперечного сечения трубопровода и соответственно скорости движения жидкости происходит превращение энергии: при сужении трубопровода часть потенциальной энергии давления переходит в кинетическую и, наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, но общее количество энергии остается постоянным. Отсюда следует, что для идеальной жидкости количество энергии, поступающей с потоком через начальное сечение трубопровода, равно количеству энергии, удаляющейся с потоком через конечное сечение трубопровода.
Таким образом, уравнение Бернулли является частым случаем закона сохранения энергии и выражает энергетический баланс потока.
Если умножить левую и правую части уравнения (II,50) на удельный вес жидкости g = rg, то уравнение Бернулли для идеальной жидкости может быть представлено в виде
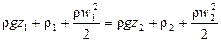
В уравнении (II,50а) каждый член выражает удельную энергию в данной точке, отнесенную не к единице веса, а к единице объема жидкости (1 м 3 ). Например
В случае горизонтально расположенного трубопровода z1 = z2 и уравнение Бернулли для идеальной жидкости упрощается:
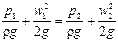

Пусть для точек, лежащих на оси трубопровода в поперечных сечениях 1—1 и 2—2, нивелирные высоты равны z1 и z2 соответственно. Установим в каждой из этих точек две вертикальные открытые так называемые пьезометрические трубки, у одной из которых нижний конец загнут навстречу потоку жидкости в трубопроводе.
В прямых вертикальных трубках (с незагнутыми нижними концами) жидкость поднимается на высоту, отвечающую гидростатическому давлению в точках их погружения, т.е. эти трубки будут измерять пьезометрические напоры в соответствующих точках.
В трубках с нижними концами, направленными навстречу потоку, уровень жидкости будет выше, чем в соседних вертикальных трубках, так как трубки с загнутыми концами будут показывать сумму пьезометрического и динамического (скоростного) напоров. Однако, согласно уравнению (II,49), во всех трубках с загнутыми нижними концами жидкость поднимается на одну и ту же высоту относительно произвольной горизонтальной плоскости сравнения, равную гидродинамическому напору Н (рис. II-15).
Площадь поперечного сечения 2—2 трубопровода меньше сечения 1—1. Поэтому скорость жидкости w2 при данном ее расходе, согласно уравнению неразрывности потока, будет больше w1. Соответственно 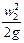
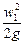
В любом поперечном сечении трубопровода скоростной напор можно измерить по разности показаний установленных здесь трубок (с загнутым и прямым нижними концами). Следовательно, эта разность должна быть больше для сечения 2—2, чем для сечения 1—1. Вместе с тем из уравнения Бернулли следует, что высота уровня жидкости в прямой трубке в сечении 2—2 должна быть меньше соответствующей высоты в прямой трубке сечения 1—1 настолько же, насколько скоростной напор в сечении 2 – 2 больше, чем в сечении 1—1.
Приведенный пример демонстрирует взаимный переход потенциальной энергии в кинетическую и, наоборот, при изменении площади сечения трубопровода, а также постоянство суммы этих энергий в любом поперечном сечении трубопровода.
При движении реальных жидкостей начинают действовать силы внутреннего трения, обусловленные вязкостью жидкости и режимом ее движения, а также силы трения о стенки трубы. Эти силы оказывают сопротивление движению жидкости. На преодоление возникающего гидравлического сопротивления должна расходоваться некоторая часть энергии потока. Поэтому общее количество энергии потока по длине трубопровода будет непрерывно уменьшаться вследствие перехода потенциальной энергии в потерянную энергию — затрачиваемую на трение и безвозвратно теряемую при рассеивании тепла в окружающую среду.
При этом для двух любых сечений 1—1 и 2—2 трубопровода, расположенных по ходу движения реальной жидкости (рис. II-15)
При движении реальной жидкости высоты ее подъема (относительно плоскости сравнения) в трубках с концами, обращенными навстречу потоку, уже не будут равны в сечениях 1—1 и 2—2, как было показано на рис. II-15 применительно к движению идеальной жидкости. Разность высот в этих трубках, обусловленная потерями энергии на пути жидкости от сечения 1—1 до сечения 2—2, характеризует потерянный напор hп.
Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения (II,50) должен быть введен член, выражающий потерянный напор. Тогда получим уравнение Бернулли для реальных жидкостей:
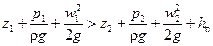
Потерянный напор hп характеризует удельную (т.е. отнесенную к единице веса жидкости) энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.
Уравнение (II,52) может быть представлено в несколько ином виде, если умножить обе его части на pg:
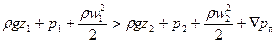
В уравнении (II,52а) величина Ñрп — потерянное давление, равное
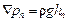
Определение потерь напора или давления является практически важной задачей, связанной с расчетом энергии, которая необходима для перемещения реальных жидкостей при помощи насосов, компрессоров и т.д. Трудность решения этой задачи обусловлена тем, что решение системы дифференциальных уравнений, описывающих движение реальной жидкости, в большинстве случаев оказывается невозможным.
Дата добавления: 2016-02-16 ; просмотров: 2749 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Дифференциальное уравнение Эйлера
Напомним, что необходимым условием существования у дифференцируемой функции экстремума в некоторой точке является равенство нулю производной в этой точке: , или, что то же самое, равенство нулю дифференциала функции .
Нашей ближайшей целью будет найти аналог этого условия в вариационном исчислении и выяснить, какому необходимому требованию должна удовлетворять функция, дающая экстремум функционалу.
Мы покажем, что такая функция должна удовлетворять некоторому дифференциальному уравнению. Форма уравнения будет зависеть от вида рассматриваемого функционала. Изложение мы начнем с так называемого простейшего интеграла вариационного исчисления, под которым подразумевают функционал, имеющий следующее интегральное представление:
Функция , стоящая под знаком интеграла, зависит от трех аргументов . Будем считать ее определенной и дважды непрерывно дифференцируемой по аргументу для всех значений, по аргументам же и — в некоторой области плоскости . Ниже предполагается, что мы всегда будем находиться внутри этой области.
Под понимается некоторая функция от
непрерывно дифференцируемая на отрезке , и есть производная от нее.
Геометрически функцию можно изобразить в плоскости некоторой линией , лежащей над отрезком (рис. 3).
Интеграл (9) является обобщением интегралов (3) и (6), с которыми мы встретились в задачах о линии наискорейшего ската и поверхности вращения наименьшей площади. Значение его зависит от выбора функции или от линии , и задача о его минимуме имеет следующий смысл.
Дано некоторое множество функций (10) (линий ). Среди них нужно найти ту функцию (линию ), для которой интеграл имеет наименьшее значение.
Мы должны прежде всего точно определить множество функций, для которых мы будем рассматривать значение интеграла (9). Функции этого множества в вариационном исчислении обычно называют допустимыми к сравнению. Рассмотрим задачу с закрепленными граничными значениями. Множество допустимых функций определяется здесь двумя следующими требованиями:
1) функция непрерывно дифференцируема на отрезке ;
2) на концах отрезка функция принимает заданные наперед значения
В остальном функция может быть совершенно произвольной. Если говорить языком геометрии, мы рассматриваем всевозможные гладкие линии, лежащие над промежутком , которые проходят через две точки и и могут быть заданы уравнением (10). Функцию, доставляющую минимум интегралу, будем считать существующей и назовем ее .
Следующие простые и остроумные соображения, часто применяемые в вариационном исчислении, дают возможность весьма просто выяснить необходимое условие, которому должна удовлетворять . По сути дела они позволяют задачу о минимуме интеграла (9) привести к задаче о минимуме функции.
Рассмотрим семейство функций, зависящее от численного параметра
Чтобы функция при любом была допустимой функцией, мы должны считать непрерывно дифференцируемой и обращающейся в нуль на концах отрезка
Интеграл (9), вычисленный для , будет некоторой функцией параметра
Разность называют вариацией (изменением) функции и обозначают , а разность — полной вариацией интеграла (9). Отсюда и произошло название вариационного исчисления.
Так как функция дает минимальное значение интегралу, то функция должна иметь минимум при , и производная от нее в этой точке обязана обращаться в нуль
Последнее равенство должно выполняться при всякой непрерывно дифференцируемой функции , обращающейся в нуль на концах отрезка . Для получения вытекающего отсюда следствия удобнее второй член в условии (14) преобразовать интегрированием по частям
и придать условию (14) другую форму
Может быть доказана следующая простая лемма.
Пусть выполняются условия:
1) функция непрерывна на отрезке ;
2) функция непрерывно дифференцируема на отрезке и на концах отрезка обращается в нуль.
Если при любой такой функции интеграл равен нулю, то отсюда следует, что .
Действительно, допустим, что в некоторой точке с функция отлична от нуля, и покажем, что тогда заведомо существует такая функция , для которой , вопреки условию леммы.
Так как и непрерывна, наверное существует около точки такой промежуток , в котором будет всюду отличной от нуля и, стало быть, сохранять знак.
Всегда можно построить функцию , непрерывно дифференцируемую на , положительную на и равную нулю всюду вне (рис. 4).
Такой будет, например, , определенная равенствами
Но для такой функции
Последний же интеграл не может быть равен нулю, так как произведение внутри промежутка интегрирования отлично от нуля и сохраняет знак.
Ввиду того, что равенство (15) должно выполняться для всякой , непрерывно дифференцируемой и обращающейся в нуль на концах отрезка , мы можем, согласно лемме, утверждать, что это может быть только в том случае, когда
или после вычисления производной по переменной
Равенство это является дифференциальным уравнением 2-го порядка относительно функции . Оно называется уравнением Эйлера .
Мы можем сделать следующее заключение.
Если функция доставляет интегралу минимум, то она должна удовлетворять дифференциальному уравнению Эйлера (17). Последнее в вариационном исчислении имеет значение, вполне сходное со значением необходимого условия в теории экстремумов функций. Оно позволяет сразу отбросить все допустимые функции, которые этому условию не удовлетворяют, так как на них интеграл заведомо не может достигать минимума. Этим очень сильно сужается круг допустимых функций, подлежащих изучению. Свое внимание мы можем сосредоточить только на решениях уравнения (17).
Сами решения уравнения (17) обладают тем свойством, что производная
для них обращается в нуль при любых , и они аналогичны по своему значению стационарным точкам функции. Поэтому часто говорят, что на решениях (17) интеграл имеет стационарное значение.
В нашей задаче с закрепленными граничными значениями нужно найти далеко не все решения эйлерова уравнения, а только те из них, которые принимают предписанные значения в точках .
Обратим внимание на то, что уравнение Эйлера (17) имеет 2-й порядок. Общее его решение будет содержать две произвольные постоянные
Их нужно определить так, чтобы интегральная кривая проходила через точки и , что доставляет два уравнения для нахождения постоянных и
Во многих случаях эта система имеет только одно решение, и тогда будет существовать только одна интегральная линия, проходящая через точки и .
Разыскание функций, подозрительных на минимум интеграла, мы привели к решению следующей граничной задачи дифференциальных уравнений: на отрезке нужно найти те решения уравнения (17), которые на концах этого отрезка принимают заданные значения .
Часто эту последнюю задачу удается решить при помощи методов, известных в теории дифференциальных уравнений.
Еще раз указываем на то, что каждое решение такой граничной задачи может только подозреваться на минимум и в дальнейшем еще надлежит проверить, будет ли оно или не будет доставлять минимальное значение интегралу. Но в частных случаях, особенно часто встречающихся в приложениях, уравнение Эйлера вполне решает задачу о нахождении минимума интеграла. Пусть нам заранее будет известно, что функция, доставляющая минимум интегралу, существует, и мы допустим, кроме того, что уравнение Эйлера (17) имеет только одно решение, удовлетворяющее граничным условиям (11), и, стало быть, только одна допустимая линия может быть заподозрена на минимум. При этих условиях можно быть уверенным в том, что найденное решение уравнения (17) действительно дает минимум интегралу.
Пример . Ранее было установлено, что [url]задача о линии наискорейшего ската[/url] может быть приведена к нахождению минимума интеграла
на множестве функций, удовлетворяющих граничным условиям .
http://helpiks.org/7-10101.html
http://mathhelpplanet.com/static.php?p=differentsialnoe-uravnenie-eilera