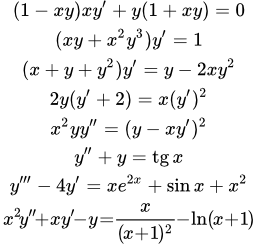Дифференциальные уравнения и ряды примеры

Примеры дифференциальных уравнений с решениями

Попробуйте решить приведенные ниже дифференциальные уравнения.
Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0\]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Дифференциальные уравнения, ряды, теория вероятности

Контрольная работа № 5 «Числовые и функциональные ряды»

В задачах 501-510 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.

506.

Применяем признак Даламбера:

Таким образом, так как , то данный ряд сходится по признаку Даламбера.

В задачах 521-540 дан степенной ряд

Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения а, b и k даны.

527.

Имеем степенной ряд .

Первые четыре члена ряда:

Применяем признак Даламбера:

Как видно, ряд будет сходиться для тех значений х, для которых

Выясним вопрос о сходимости ряда на концах интервала.

При ряд примет вид — знакочередующийся; его общий член по абсолютному значению стремиться к нулю при n®¥. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд сходится. Следовательно, значение принадлежит области сходимости данного ряда.

Подставив в , получим — расходится (для этого достаточно сравнить его с гармоническим рядом). Следовательно, значение не принадлежит области сходимости данного ряда. Таким образом, — область сходимости исследуемого ряда.

В задачах 541-560 требуется вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

558.

Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции cos(x), будем иметь

Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде третий член по абсолютному значению меньше 0,001, то ограничиваемся только первыми двумя членами. Итак,

В задачах 561-572 разложить в ряд Фурье периодическую функцию f(x), заданную на интервале-периоде

571.

Заданная функция f(x) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство

Где an и bn определяются по формулам

Коэффициент а0:

Определим коэффициенты аn:

Интегрируя по частям, получаем

Определим коэффициенты bn:

Интегрируя по частям, получаем

Подставляя найденные значения коэффициентов Фурье в формулу , получаем

Контрольная работа № 6 «Дифференциальные уравнения»

В задачах 581-590 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.

590.

Данное уравнение является однородным, так как коэффициенты при dx и dy суть однородные функции одного и того же измерения (второго) относительно переменных х и у. Применяем подстановку у=хt, где t – некоторая функция аргумента х.

Если у=хt, то дифференциал dy=d(xt)=tdx+xdt, и данное уравнение примет вид

Мы получили уравнение с разделенными переменными относительно х и t. Интегрируя, находим общее решение этого уравнения:

Из введенной подстановки следует, что у=хt. Следовательно, или — общее решение данного уравнения.

В задачах 601-620 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.

611.

Данное уравнение второго порядка не содержит явно аргумента х. Положим у’=р, где р – некоторая функция переменной у. Если у’=р, то . Тогда данное уравнение примет вид

Тогда при — решение данного уравнения.

При — уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

Обратная подстановка у’=р. Тогда

Используя начальные условия , находим С1:

Далее решаем уравнение :

Теперь определим значение С2:

Тогда — искомое частное решение, удовлетворяющее указанным начальным условиям.

В задачах 621-640 даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.

622.

Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.

Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 4r = 0

Корни характеристического уравнения: r1 = 0, r2 = -4.

Следовательно, фундаментальную систему решений составляют функции: y1 = e-4x, y2 = e0x

Общее решение однородного уравнения имеет вид:

Правая часть F(x) =

Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы

Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))

Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).

Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.

Следовательно, число α+βi=0+1i не является корнем характеристического уравнения.

Уравнение имеет частное решение вида:

Вычисляем производные: ,

Которые подставляем в исходное дифференциальное уравнение:

Приравнивая коэффициенты при одинаковых функциях, получаем систему уравнений:

Частное решение имеет вид:

Тогда общее решение данного уравнения

Используем начальные условия

. Тогда

Окончательно,

Ответ:

В задачах 661-680 при указанных начальных условиях найти три первых, отличных от нуля члена разложения в степенной ряд функции y=f(x), являющейся решением заданного дифференциального уравнения.

662.

Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если у(х) допускает разложение в ряд Маклорена, то имеем

(1)

Свободный член разложения (1), т. е. у(0), дан по условию. Чтобы найти значения y'(0), y’’(0), y’’’(0),…, можно данное уравнение последовательно дифференцировать по переменной х и затем вычислить значения производных при х=0.

Значение у’(0) получаем, подставив начальные условия в данное уравнение:

Подставив найденные значения производных при х=0 в (1), получим разложение искомого частного решения заданного уравнения:

или

Контрольная работа № 7 «Вероятность и законы распределения»

691. На химзаводе расположены 5 складов с продукцией. Вероятность возникновения пожара в каждом из них в течение года равна 0,03. Построить график функции распределения для складов, на которых ежегодно бывают пожары.

Используем формулу Бернулли

Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события равна q=1-p, то вероятность Рп(т) того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле

где есть число сочетаний из п элементов по т.

По условию задачи возникновения пожара в каждом из складов в течение года равна р=0,03; тогда q=0,97; в данном случае п=5 и. Подставляя эти данные в формулу Бернулли (1), получим

При m=0

При m=1

При m=2

При m=3

При m=4

При m=5

В задачах 711-720 дано, что на заводе рабочий за смену изготовляет n деталей. Вероятность того, что деталь окажется первого сорта равна р. Какова вероятность, что деталей первого сорта будет m штук.

716.

Применим локальную теорему Муавра-Лапласа, согласно которой искомая вероятность вычисляется приближенно по формуле где

Так как функция j(х) четная, то j(-х)=j(х).

Подставим сюда числовые значения: n=192, p=0,75, m=150.

Определяем значение х при этих данных:

По таблице находим, что j(1)=0,2420. Подставив это значение в получим

Ответ:

В задачах 731-740 дано, что детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали (математическое ожидание) равна а мм, среднее квадратическое отклонение — s мм. Найти: 1) вероятность того, что диаметр наудачу взятой детали будет больше a мм и меньше b мм; 2) вероятность того, что диаметр детали отклонится от стандартной длины не более чем на d мм. Значения а, s, a, b, d даны.

Если величина Х распределена по нормальному закону, то

Где а=М(Х) и . По условию s=4, a=30 и b=40. Подставив эти данные, получим

Если Х – длина диаметра детали, то по условию задачи эта величина должна быть в интервале (а-d, а+d), где а=36 и d=2. Подставив в формулу A=а-d и b=а+d, получим

Таким образом,

Подставляя имеющиеся данные, получим

Итак, вероятность того, что изготовление детали по длине будут в пределах от 34 до 38 см, составляет 0,383

В задачах 741-760 задан закон распределения случайной величины Х (в первой строке таблицы даны возможные значения величины Х, а во второй строке указаны вероятности р этих возможных значений).

Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X); 3) среднее квадратическое отклонение s.

Математическое ожидание М(Х) вычисляется по формуле

Тогда М(Х) = 18·0,2+22·0,3+23·0,4+26·0,1=3,6+6,6+9,2+2,6=22

Дисперсию D(X) найдём по формуле

Для вычисления составим следующий закон распределения величины :

Тогда и

Среднее квадратическое отклонение найдём по формуле

Из этой формулы имеем:

Контрольная работа № 5 «Числовые и функциональные ряды»

В задачах 501-510 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.

507.

Применяем признак Даламбера:

Таким образом, так как , то данный ряд сходится по признаку Даламбера.

В задачах 521-540 дан степенной ряд

528.

Имеем степенной ряд .

Первые четыре члена ряда:

Применяем признак Даламбера:

Как видно, ряд будет сходиться для тех значений х, для которых

Выясним вопрос о сходимости ряда на концах интервала.

При ряд Примет вид — знакочередующийся; его общий член по абсолютному значению стремиться к нулю при n®¥. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд сходится. Следовательно, значение принадлежит области сходимости данного ряда.

559.

Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции , будем иметь

В задачах 561-572 разложить в ряд Фурье периодическую функцию f(x), заданную на интервале-периоде

572.

Заданная функция f(x) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство

Где an и bn определяются по формулам

Определим коэффициенты аn:

Определим коэффициенты bn:

Подставляя найденные значения коэффициентов Фурье в формулу , получаем

Контрольная работа № 6 «Дифференциальные уравнения»

В задачах 581-590 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.

581.

Данное уравнение является однородным, так как коэффициенты при dx и dy суть однородные функции одного и того же измерения (первого) относительно переменных х и у. Применяем подстановку у=хt, где t – некоторая функция аргумента х.

Если у=хt, то дифференциал dy=d(xt)=tdx+xdt, и данное уравнение примет вид

Тогда

Из введенной подстановки следует, что у=хt. Следовательно, или — общее решение данного уравнения.

612.

Данное уравнение второго порядка не содержит явно аргумента х. Положим у’=р, где р – некоторая функция переменной у. Если у’=р, то . Тогда данное уравнение примет вид — уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

Обратная подстановка у’=р. Тогда

Используя начальные условия , находим С1:

Далее решаем уравнение :

Теперь определим значение С2:

Тогда — искомое частное решение, удовлетворяющее указанным начальным условиям.

623.

Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 –r-2 = 0

Корни характеристического уравнения: r1 = -1, r2 = 2.

Следовательно, фундаментальную систему решений составляют функции: y1 = e-1x, y2 = e2x

Общее решение однородного уравнения имеет вид:

Правая часть F(x) =

Поиск частного решения.

Уравнение имеет частное решение вида:

Вычисляем производные: ,

Которые подставляем в исходное дифференциальное уравнение:

Приравнивая коэффициенты при одинаковых функциях, получаем систему уравнений:

Частное решение имеет вид:

Тогда общее решение данного уравнения

Используем начальные условия

Тогда решим систему:

Окончательно,

Ответ:

663.

(1)

Значение у’(0) получаем, подставив начальные условия в данное уравнение:

или

Контрольная работа № 7 «Вероятность и законы распределения»

692. Автоматическая пожарная сигнализация установлена в помещениях. Вероятность возникновения пожара в каждом из помещений в течение года равна РП=0,5. Сигнализация обнаруживает загорание с вероятностью РС=0,06. Вероятность срабатывания без пожара равна РОШ=0,07. Найти вероятность наличия загорания при условии, что сигнализация сработала.

В соответствии с Формулами Байеса, вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на условную вероятность события по этой гипотезе, деленному на полную вероятность события:

В нашей задаче событие А – сигнализация сработала; гипотезы Н1 – возник пожар; Н2 – пожара не было.

Априорные (доопытные) вероятности гипотез нам известны: Р(Н1)=0,5; Р(Н2)=0,5. Условные вероятности срабатывания сигнализации при этом даны: Р(А/Н1)=0,06; Р(А/Н2)=0,07. Полная вероятность попадания в цель Р(А)= 0,5*0,06+0,5*0,07=0,065

Тогда апостериорная (послеопытная) вероятность гипотезы Н1 – возник пожар будет равна

;

Ответ:

717.

Применим локальную теорему Муавра-Лапласа, согласно которой искомая вероятность вычисляется приближенно по формуле

где

Так как функция j(х) четная, то j(-х)=j(х).

Подставим сюда числовые значения: n=225, p=0.8, m=165.

Определяем значение х при этих данных:

По таблице находим, что j(2,5)=0,0175. Подставив это значение в получим

Ответ:

Если величина Х распределена по нормальному закону, то

Где а=М(Х) и . По условию s=5, a=54 и b=70. Подставив эти данные, получим

Если Х – длина диаметра детали, то по условию задачи эта величина должна быть в интервале (а-d, а+d), где а=60 и d=8. Подставив в формулу A=а-d и b=а+d, получим

Таким образом,

Подставляя имеющиеся данные, получим

Итак, вероятность того, что изготовление детали по длине будут в пределах от 52 до 68 см, составляет

Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X); 3) среднее квадратическое отклонение s.

Математическое ожидание М(Х) вычисляется по формуле

Тогда М(Х) = 78·0,2+80·0,3+84·0,1+85·0,4=15,6+24+8,4+34=82.

Дисперсию D(X) найдём по формуле

Для вычисления составим следующий закон распределения величины :

Тогда и

Среднее квадратическое отклонение найдём по формуле

Из этой формулы имеем:

Контрольная работа № 5 «Числовые и функциональные ряды»

В задачах 511-520 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.

516.

Применяем интегральный признак Коши, для этого посчитаем соответствующий несобственный интеграл:

Следовательно, исходный ряд сходится по интегральному признаку Коши.

В задачах 521-540 дан степенной ряд

537.

Имеем степенной ряд .

Первые четыре члена ряда:

Применяем признак Даламбера:

Как видно, ряд будет сходиться для тех значений х, для которых

Выясним вопрос о сходимости ряда на концах интервала.

548.

Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции cos(x), будем иметь , тогда ,

В задачах 561-572 разложить в ряд Фурье периодическую функцию f(x), заданную на интервале-периоде

561.

Заданная функция f(x) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство

Где an и bn определяются по формулам

Определим коэффициенты аn:

Определим коэффициенты bn:

Подставляя найденные значения коэффициентов Фурье в формулу , получаем

Контрольная работа № 6 «Дифференциальные уравнения»

В задачах 591-600 Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.

600.

Данное уравнение является линейным, так как оно содержит искомую функцию У и ее производную У’ в первой степени и не содержит их произведений.

Применяем подстановку У=Uv, где U и V – некоторые неизвестные функции аргумента Х. Если У=Uv, то Y’=(Uv)’=U’V+Uv’ и данное уравнение примет вид Или (1)

Так как искомая функция У представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию U так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т. е. выберем функцию U так, чтобы имело место равенство (2)

При таком выборе функции U уравнение (1) примет вид (3)

Уравнение (2) есть уравнение с разделяющимися переменными относительно U и Х. Решим это уравнение:

(Чтобы равенство(2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0). Подставив в (3) найденное выражение для U, получим:. Тогда — общее решение данного уравнения.

Используем условие

Окончательно

601.

Данное дифференциальное уравнение второго порядка не содержит явно функцию У. Положим У’=Р, где Р – некоторая функция аргумента Х. Если У’=Р, то и данное уравнение примет вид . Мы получили уравнение первого порядка относительно переменных Р и Х. Решим это уравнение.

Применяем подстановку Р=Uv, где U и V – некоторые неизвестные функции аргумента Х. Р’=(Uv)’=U’V+Uv’ и данное уравнение примет вид

Подставив в уравнение получим

Тогда . Обратная подстановка

Определим численное значение С При указанных начальных условиях. Имеем . Теперь решаем уравнение первого порядка :

Определим численное значение С2 при указанных начальных условиях. Имеем .

Таким образом, есть частное решение, удовлетворяющее указанным начальным условиям.

639.

Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 6r +9= 0

Корни характеристического уравнения: r1 = -3, r2 = -3.

Общее решение однородного уравнения имеет вид:

Правая часть F(x) =

Уравнение имеет частное решение вида:

Которые подставляем в исходное дифференциальное уравнение:

Частное решение имеет вид:

Тогда общее решение данного уравнения

Используем начальные условия

Окончательно,

Ответ:

672.

(1)

Значение у’(0) получаем, подставив начальные условия в данное уравнение:

или

Контрольная работа № 7 «Вероятность и законы распределения»

681. Автоматическая пожарная сигнализация установлена в помещениях. Вероятность возникновения пожара в каждом из помещений в течение года равна РП=0,05. Сигнализация обнаруживает загорание с вероятностью РС=0,85. Вероятность срабатывания без пожара равна РОШ=0,012. Найти вероятность наличия загорания при условии, что сигнализация сработала.

В соответствии с формулой Байеса, вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на условную вероятность события по этой гипотезе, деленному на полную вероятность события:

В нашей задаче событие А – сигнализация сработала; гипотезы Н1 – возник пожар; Н2 – пожара не было.

Априорные (доопытные) вероятности гипотез нам известны: Р(Н1)=0,05; Р(Н2)=1-Р(Н1)=1-0,05=0,95. Условные вероятности срабатывания сигнализации при этом даны: Р(А/Н1)=0,85; Р(А/Н2)=0,012. Полная вероятность попадания в цель

Тогда апостериорная (послеопытная) вероятность гипотезы Н1 – возник пожар будет равна

;

Ответ:

705. Принимая вероятности рождения мальчика и девочки одинаковыми, найти вероятность того, что среди 6 новорожденных: а) 4 мальчика; б) не более двух девочек.

Используем формулу Бернулли

Если производится n независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события равна q=1-p, то вероятность того, что при этом событие осуществляется ровно m раз, вычисляется по формуле где есть число сочетаний из n элементов по m.

По условию задачи вероятности рождения мальчика и девочки одинаковы, тогда р=0,5; тогда q=0,5;Подставляя эти данные в формулу Бернулли, получим

Б) не более двух девочек.

Ответ: а) 4 мальчика б) не более двух девочек

В задачах 721-730 дана вероятность Р появления события А в каждом из П независимых испытаний. Пользуясь интегральной теоремой Лапласа, найти вероятность того, что в этих испытаниях событие А появится не менее M1 раз и не более M2 раза.

724.

Так как вероятность наступления события А в каждом из П независимых испытаний постоянна и равна р=0,4, а число n=600 достаточно велико, то вероятность того, что событие А в таких испытаниях наступит не менее Т1 раз и не более Т2 раз, вычисляется приближенно по формуле

, где

Эта функция является нечетной, т. е. Ф(-х)=-Ф(х). Если воспользоваться готовыми значениями функции Лапласа, то формулу можно записать так:

По таблице находим Ф(1)=0,3413; Ф(-2,5)=-Ф(2,5)=-0,4938. Подставив эти значения, получим искомую вероятность:

Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X); 3) среднее квадратическое отклонение s.

Математическое ожидание М(Х) вычисляется по формуле

Тогда М(Х) = 24·0,2+26·0,2+28·0,5+30·0,1=4,8+5,2+14+3=27

Дисперсию D(X) найдём по формуле

Для вычисления составим следующий закон распределения величины :

Тогда и

Среднее квадратическое отклонение найдём по формуле

Из этой формулы имеем:

Контрольная работа № 5 «Числовые и функциональные ряды»

В задачах 501-510 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.

510.

Применяем признак Даламбера:

Таким образом, так как , то данный ряд расходится по признаку Даламбера.

В задачах 521-540 дан степенной ряд

521.

Имеем степенной ряд .

Первые четыре члена ряда:

Применяем признак Даламбера:

Как видно, ряд будет сходиться для тех значений х, для которых

Выясним вопрос о сходимости ряда на концах интервала.

552.

Тогда ,

575. Функцию в интервале (0, 1) разложить в ряд синусов.

Так как по условию ряд заданной функции должен содержать только синусы кратных дуг, то продолжим функцию в интервале (-1;0) нечетным образом. В результате будет получена нечетная функция, которая совпадает с заданной на интервале (0;1). Известно, что ряд Фурье для нечетной функции имеет вид где bn определяется по формуле

Определим коэффициенты bn:

Подставляя найденное значение коэффициентов Фурье в формулу , получаем

Контрольная работа № 6 «Дифференциальные уравнения»

В задачах 581-590 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.

584.

Если у=хt, то дифференциал dy=d(xt)=tdx+xdt, и данное уравнение примет вид

Из введенной подстановки следует, что у=хt. Следовательно, или — общее решение данного уравнения.

615.

Обратная подстановка у’=р. Тогда

Используя начальные условия , находим С1:

Далее решаем уравнение :

Теперь определим значение С2:

Тогда — искомое частное решение, удовлетворяющее указанным начальным условиям.

626.

Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2–4=0

Корни характеристического уравнения: r1 = 2, r2 = -2.

Общее решение однородного уравнения имеет вид:

Уравнение имеет частное решение вида:

Вычисляем производные: ,

Которые подставляем в исходное дифференциальное уравнение:

Приравнивая коэффициенты при одинаковых функциях, получаем систему уравнений:

Частное решение имеет вид:

Тогда общее решение данного уравнения

Используем начальные условия

Тогда решим систему:

Окончательно,

Ответ:

666.

(1)

Значение у’(0) получаем, подставив начальные условия в данное уравнение:

или

Контрольная работа № 7 «Вероятность и законы распределения»

695. На территории региона работают 4 атомных станции. Расчетная вероятность возникновения в течение года инцидентов, связанных с пожарами, составляет 0,03; с выходом из строя электрооборудования – 0,05; прорывом трубопроводов – 0,08. Найти вероятность того, что в течение года не будет инцидентов по этим причинам.

Вероятность того, что в течение года не будет инцидентов, связанных с пожарами , с выходом из строя электрооборудования ; прорывом трубопроводов .

По теореме умножения вероятностей независимых событий вероятность того, что в течение года не будет инцидентов по этим причинам:

Ответ:

720.

где

Так как функция j(х) четная, то j(-х)=j(х).

Подставим сюда числовые значения: .

Определяем значение х при этих данных:

По таблице находим, что j(1)=0,2420. Подставив это значение в получим

Ответ:

Если величина Х распределена по нормальному закону, то

Где а=М(Х) и . По условию s=4, a=27 и b=37. Подставив эти данные, получим

Если Х – длина диаметра детали, то по условию задачи эта величина должна быть в интервале (а-d, а+d), где а=35 и d=2. Подставив в формулу A=а-d и b=а+d, получим

Таким образом,

Подставляя имеющиеся данные, получим

Итак, вероятность того, что изготовление детали по длине будут в пределах от 33 до 37 см, составляет

Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X); 3) среднее квадратическое отклонение s.

источники:

http://nauchniestati.ru/spravka/primery-resheniya-differenczialnyh-uravnenij-s-otvetami/

http://matica.org.ua/primery/primery/differentcialnye-uravneniia-riady-teoriia-veroiatnosti