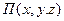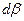Дифференциальные уравнения идеальной жидкости это уравнения

Уравнение Бернулли. Дифференциальные уравнения движения идеальной жидкости

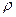
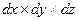
В движущейся идеальной жидкости, плотность которой , выделим элементарный параллелепипед размерами и запишем дифференциальные уравнения движения этого объема жидкости в координатной форме, рассматривая его как материальную точку.

На элемент действуют составляющие сил давления и массовых сил, интенсивность которых на единицу массы по направлению осей равна 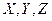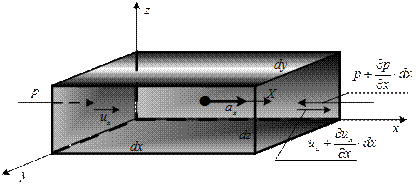(рис. 6.1).

Рис. 6.1

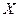
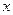
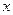
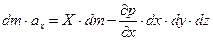На рисунке показаны только составляющая массовых сил по оси , давление на гранях перпендикулярных оси и составляющая ускорения по оси , что позволяет записать уравнение движения выделенного объема в направлении оси

.

(6.1)

Так как масса элементарного объема легко определяется через массовую плотность

,

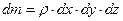(6.2)

то после деления обеих частей уравнения (6.1) на (6.2), получаем

.

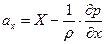(6.3)

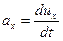
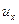
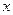
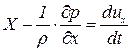С учетом того, что , где – проекция скорости элементарного объема на ось , уравнение (6.3) принимает вид

.

(6.4)

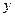
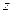
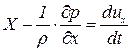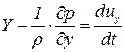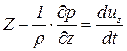Действуя аналогично можно получить уравнения движения выделенного элемента в направлении осей и . Таким образом система дифференциальных уравнений движения идеальной жидкости в декартовой прямоугольной системе координат имеет вид

, ,

(6.5)

Уравнение Бернулли для установившегося движения при действии

Последовательно умножим уравнения (6.5) на и сложим полученные результаты

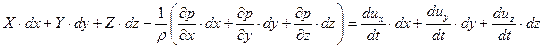(6.6)

При установившемся движении

,

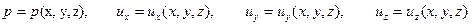(6.7)

тогда в рассматриваемый момент времени

.

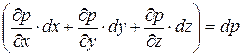(6.8)

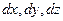
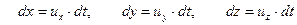В движущейся жидкости размеры элементарного параллелепипеда можно определить через составляющие скорости частицы

.

(6.9)

С учетом (6.9) правая часть уравнения (6.6) приводится к виду

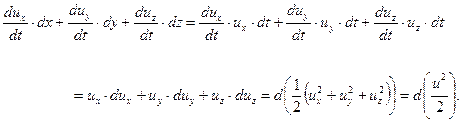(6.10)

Если движение жидкости происходит в потенциальном силовом поле, то составляющие интенсивности массовых сил определяются через потенциальную энергию этого поля, приведенную к единице массы

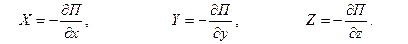(6.11)

Принимая во внимание (6.11), первое слагаемое в левой части уравнения (6.6) можно записать так

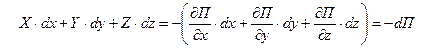(6.12)

С учетом (6.8), (6.10), (6.12) уравнение (6.6) принимает следующий вид

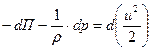(6.13)

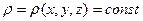
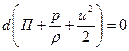Так как идеальная жидкость – это несжимаемая жидкость, и (6.13) можно записать в виде

,

(6.14)

.

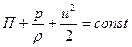(6.15)

Уравнение (6.15) и является уравнением Бернулли для элементарной струйки идеальной жидкости при установившемся движении, когда элементарную струйку можно отождествлять с линией тока. Для различных линий тока значения константы в уравнении (6.15) будут разными.

Замечание. Более детальное изучение движения частицы жидкости позволяет установить, что при изменении положения в пространстве происходит изменение ее формы и объема. Движение можно представить как сумму трех движений: поступательного (вместе с полюсом), деформационного (за счет изменения размеров) и вращательного (вокруг мгновенной оси, проходящей через полюс).

По характеру движения частиц различаютвихревое и потенциальное движения.

Вихревым движением называют такое движение, при котором движущиеся частицы жидкости вращаются вокруг осей, проходящих через их полюсы. Вихревое движение характеризуется вихревыми линиями – линиями, в каждой точке которых касательная совпадает с вектором угловой скорости .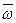

Движение, при котором такое вращение отсутствует, называется безвихревым или потенциальным движением.

Уравнение Бернулли справедливо:

· вдоль линии тока;

· на вихревых линиях;

· при винтовом движении, когда векторы линейной и угловой скоростей параллельны (линия тока совпадает с вихревой линией);

· при потенциальном движении;

· при статическом равновесии жидкости.

Проведем детальное рассмотрение параметров, характеризующих движение жидкой частицы, но ограничимся только движением в плоскости xy (рис. 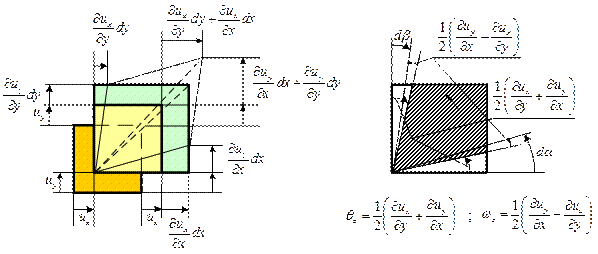6.2).

Рис. 6.2

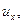
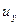
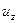
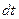
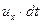
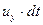
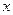
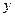
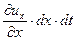Частица жидкости в форме прямоугольного параллелепипеда (рис. 6.1) имеет в точке О локальную скорость, составляющие которой равны , . Если О полюс, движущейся частицы, за время сместится на расстояние в направлении оси x и на расстояние в направлении оси y, то за счет приращения скорости в направлении осей и ребра частицы получат абсолютные удлинения: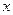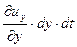

— по оси ; — по оси .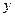

(6.16)

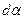
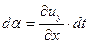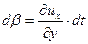Кроме деформаций удлинения частица в окрестности точки О претерпевает деформации сдвига, характеризуемые углами и

; .

(6.17)

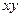
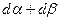
Суммарную деформацию сдвига в плоскости равную можно разложить на две составляющие:

деформацию сдвига, характеризуемую углами

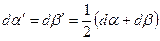(6.18)

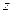
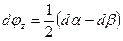и поворот частицы относительно оси , проходящей через полюс О, на угол

(6.19)

Следовательно, изменение положения и формы частицы в плоскости 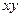характеризуется:

скоростями линейных относительных деформаций

,

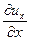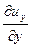(6.20)

скоростью деформации сдвига

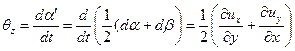(6.21)

угловой скоростью вращения частицы относительно оси

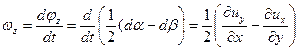(6.22)

В общем случае деформационное движение частицы характеризуется:

скоростями линейных деформаций

, , ;

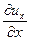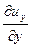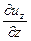(6.23)

скоростями угловых деформаций

;

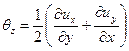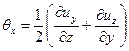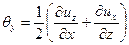(6.24)

составляющими мгновенных угловых скоростей

;

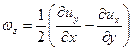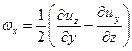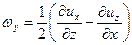(6.25)

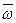
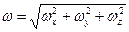Вектор мгновенной угловой скорости направлен по нормали к плоскости в которой происходит вращение, а его модуль легко определяется по составляющим

.

(6.26)

С направлением вектора 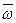связано определение вихревой линии – линии, в каждой точке которой вектор угловой скорости совпадает с направлением касательной к этой линии (рис.6.3).

Рис. 6.3

Дифференциальное уравнение вихревой линии имеет вид

,

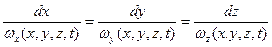(6.27)

где 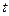рассматривается как параметр.

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера)

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера)

Дифференциальные уравнения движения идеальной жидкости (уравнения Л. Эйлера). Идеально подходит при выводе дифференциальных уравнений движения Жидкость проигнорирована frictional force. As в результате этого Главным свойством гидростатического давления является независимость От направления можно расширить до гидро Динамическое давление, т. е. Может принимать:px = pv = pv * Во-первых, абсолютное движение, то есть Связь с Землей и движение самой земли Пожалуйста, подумайте. Выберите прямоугольную частицу в потоке жидкости 5d параллелепипед с ребрами длины xx (рис. 8-4).

В рассматриваемом случае, масса Сила тяжести только-еще 80 Поверхностная сила-давление 8Р. Грани. Рассматриваемая частица перемещается в общий случай 4и ИИ. Ускорение a =здесь является производной вектора С ростом-центр частицы во времени. По законам движения Центр инерции Сила должна быть равна произведению массы bm частицы. Йи А = ускорение его центра. 2. Для стабильного движения ТХ + ды (Пу, г) +§к (пт *) =°- (8-22 Дифференциальное уравнение движения для идеальных жидкостей[> 7 Таким образом, уравнение движения является Илиде.

До сих пор неизвестно, существует ли гладкое решение уравнения Эйлера в трёхмерном случае, начиная с заданного момента времени. Людмила Фирмаль

• Чтобы получить уравнение Эйлера, преобразуйте уравнение (8-23). Для этого необходимо сначала спроектировать его на любой оси и Например, по оси x. Что купить： 80 ^ +ЗР, = Прогнозирование оставшихся войск давление на оси x равно нулю. Потому что сила перпендикулярна На оси проекции. Проекция силы тяжести на ось x ЮУ. .Где X-проекция на ось X Только гравитация рения^ .Усилие 8P, гидравлическое для определения разности 6L2 через r динамическое давление центра параллелепипеда .Потому что сила трения равна нулю Р = РХ = Ру = Р * ’ В общем случае гидродинамическое давление Р Функция координат и времени, т . е . п = п (* .г, р, *) .

В этой форме уравнение часто используется для решения различных прикладных задач гидродинамики и газодинамики. Людмила Фирмаль

• Полученные 3 уравнения являются производными Уравнения движения для идеальных жидкостей-уравнения Эйлер .Эти уравнения были получены им в 1755 году .Они правы .Привод как капельницы и газа .Над разницей Социальное уравнение движения неадекватно Количество Больше, чем число известных (p, p7, yi и yi) уравнений .Уравнение второго уравнения закрыть Настой < ?= sopz1), уравнение является непрерывным СТИ (8-21) .Для изучения движения газового потока (п ф сопз ! Необходимо пополнить систему 5-й формулой .Клапейрон-выведено уравнение состояния Менделеева.

Возьмем непрерывное уравнение в виде (8-20) .1 см .сноски на стр . 33 .L .уравнения Эйлера в натуральном виде 19 Уравнение Эйлера абсолютного движения, полученное выше Ния могут быть представлены в векторном виде .(П) =^, (8-26 Где$ вектор ускорения силы тяжести .§Gas1 (p) гидродинамический градиент давления (см .сноску Страница 38) .Правильность этой формы уравнений легко проверить Спроектируйте его по координатным осям и получите уравнение в качестве его заднего Эйлера в координатной форме .Уравнения Эйлера также могут быть использованы для следующих целей.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Идеальная жидкость и уравнения, описывающие ее движение

Раздел физики, который изучает особенности движение жидких сред, называется гидродинамикой. Одним из главных математических выражений гидродинамики является уравнение Бернулли для идеальной жидкости. Именно этой теме посвящена статья.

Что такое идеальная жидкость?

Многие знают, что жидкая субстанция представляет собой такое агрегатное состояние материи, которое сохраняет при постоянных внешних условиях объем, но изменяет свою форму при малейшем воздействии на нее. Под идеальной жидкостью понимают такую текучую субстанцию, которая не имеет вязкости и является несжимаемой. Это два главных свойства, которые отличают ее от реальных текучих сред.

Вам будет интересно: Как разобрать предложение по составу? Русский язык

Отметим, что практически все реальные жидкости можно считать несжимаемыми, поскольку для небольшого изменения их объема необходимо огромное внешнее давление. Например, если создать давление в 5 атмосфер (500 кПа), то вода увеличит свою плотность всего на 0,024 %. Что касается вопроса вязкости, то для ряда практических задач, когда в качестве рабочей жидкости рассматривается вода, ею можно пренебречь. Для полноты информации отметим, что динамическая вязкость воды при 20 oC составляет 0,001 Па*с2, что в сравнении с этой величиной для меда (>2000), является мизерным значением.

Важно не путать понятия идеальной жидкости и идеального газа, поскольку последний является легко сжимаемым.

Уравнение непрерывности

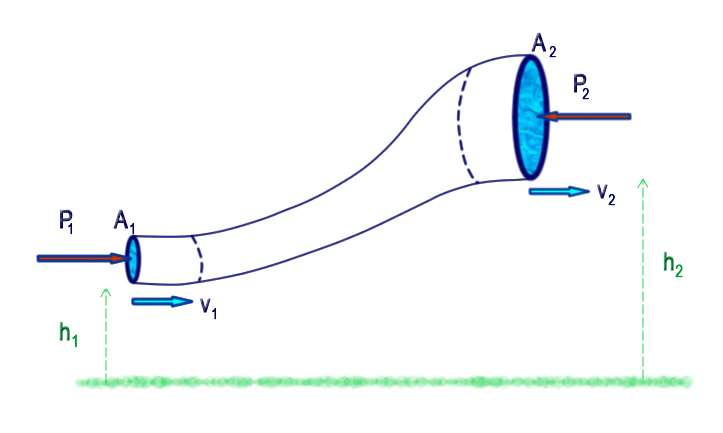
В гидродинамике движение идеальной жидкости начинают рассматривать с изучения уравнения непрерывности ее потока. Чтобы понять суть вопроса, необходимо рассмотреть движение жидкости по трубе. Представим, что на входе труба имеет площадь сечения A1, а на выходе A2.

Теперь предположим, что жидкость течет в начале трубы со скоростью v1, это означает, что за время t через сечение A1 пройдет поток объемом V1 = A1*v1*t. Поскольку жидкость является идеальной, то есть несжимаемой, то точно такой же объем воды должен выйти из конца трубы за время t, получаем: V2 = A2*v2*t. Из равенства объемов V1 и V2 следует уравнение непрерывности потока идеальной жидкости:

Из полученного уравнения следует, что если A1>A2, то v1 должно быть меньше, чем v2. Другими словами, уменьшая сечение трубы, мы тем самым увеличиваем скорость выходящего из нее потока жидкости. Очевидно, что этот эффект наблюдал каждый человек в жизни, кто хотя бы раз поливал из шланга клумбы с цветами или огород, так, прикрывая пальцем отверстие шланга, можно наблюдать, как струя бьющей из него воды становится сильнее.

Уравнение непрерывности для разветвленной трубы

Интересно рассмотреть случай движения идеальной жидкости по трубе, которая имеет не один, а два и более выхода, то есть является разветвленной. Например, площадь сечения трубы на входе равна A1, а к выходу она разветвляется на две трубы с сечениями A2 и A3. Определим скорости потоков v2 и v3, если известно, что на вход вода поступает со скоростью v1.

Используя уравнение непрерывности, получаем выражение: A1*v1 = A2*v2 + A3*v3. Чтобы решить это уравнения относительно неизвестных скоростей, нужно понимать, что на выходе, в какой бы трубе не находился поток, он движется с одинаковой скоростью, то есть v2=v3. Этот факт можно понять интуитивно. Если разделить некоторой перегородкой выходную трубу на две части, скорость потока при этом не изменится. Учитывая этот факт, получаем решение: v2 = v3 = A1*v1/(A2 + A3).

Уравнение Бернулли для идеальной жидкости

Швейцарский физик и математик голландского происхождения Даниил Бернулли в своей работе «Гидродинамика» (1734 год) представил уравнение идеальной жидкости, описывающее ее движение. Оно записывается в следующей форме:

P+ ρ*v2/2 + ρ*g*h = const.

Это выражение отражает закон сохранения энергии в случае течения жидкости. Так, первое слагаемое (P) — давление, направленное вдоль вектора перемещения жидкости, которое описывает работу потока, второе слагаемое (ρ*v2/2) — это кинетическая энергия текучей субстанции, и третье слагаемое (ρ*g*h) — это ее потенциальная энергия.

Напомним, что это уравнение справедливо для идеальной жидкости. В действительности же всегда существует трение текучей субстанции о стенки трубы и внутри ее объема, поэтому в приведенное уравнение Бернулли вводят дополнительный член, описывающий эти энергетические потери.

Использование уравнения Бернулли

Интересно привести некоторые изобретения, в которых используются выводы из уравнения Бернулли:

• Дымоход и вытяжки. Из уравнения следует, что чем больше скорость движения текучей субстанции, тем меньше ее давление. Скорость движения воздуха наверху дымохода больше, чем в его основании, поэтому поток дыма из-за разницы давлений всегда стремится вверх.
• Водопроводные трубы. Уравнение помогает понять, как изменится давление воды в трубе, если изменить диаметр последней.
• Самолеты и «Формула-1». Угол расположения крыльев самолета и антикрыла «Формулы-1» обеспечивает разность давления воздуха над и под крылом, что создает поднимающую и прижимающую силу соответственно.

Режимы течения жидкости

Уравнение Бернулли не учитывает режим движения жидкости, который может быть двух типов: ламинарный и турбулентный. Ламинарный поток характеризуется спокойным течением, при котором слои жидкости движутся по относительно плавным траекториям и не смешиваются между собой. Турбулентный режим движения жидкости характеризуется хаотичным перемещением каждой молекулы, составляющей поток. Особенностью турбулентного режима является наличие завихрений.

Каким способом будет течь жидкость, зависит от ряда факторов (особенности системы, например, наличия или отсутствия шероховатостей на внутренней поверхности трубы, вязкости субстанции и скорости ее перемещения). Переход между рассматриваемыми режимами движения описывается числами Рейнольдса.

Ярким примером ламинарного течения является медленное движение крови по гладким кровеносным сосудам. Пример турбулентного течения — сильный напор воды из крана.