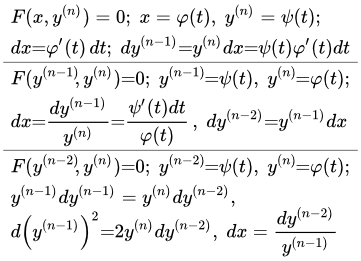Дифференциальные уравнения интегрируемые в квадратурах

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Здесь рассмотрены методы решения дифференциальных уравнений высших порядков, решаемые в квадратурах, то есть решения которых можно выразить через конечное число интегралов. К таким уравнениям относятся следующие типы:
⇓
⇓
⇓
Также приводятся подробно разобранные примеры решений ⇓ таких уравнений.

F(x, y (n) ) = 0: Дифференциальные уравнения, содержащее только независимую переменную и производную n-го порядка

Рассмотрим дифференциальное уравнение высшего порядка, содержащее только независимую переменную x и производную n-го порядка :
(1) .

y (n) = f(x) Разрешенные относительно старшей производной

Если уравнение (1) удастся разрешить относительно производной, то есть представить в виде
(1.1) ,
то оно решается непосредственным интегрированием.

x = f(y (n) ) Разрешенные относительно независимой переменной

Рассмотрим случай, когда уравнение (1) можно разрешить относительно переменной x . В этом случае, независимая переменная является функцией от старшей производной:
(1.2.1) .
Это уравнение можно решить в квадратурах в параметрическом виде, последовательно понижая порядок.

Вводим параметр t :
(1.2.2) .
Тогда из (1.2.1) получаем:
(1.2.3) .
При переходе к параметрическому виду (1.2.2) – (1.2.3), независимой переменной становится параметр t , а переменные и x – зависимыми от параметра t .

Возьмем дифференциал от (1.2.3):
;
(1.2.4) .
Выразим производную n-го порядка через производную порядка n–1 , воспользовавшись уравнением:
.
Учитывая (1.2.2), и подставляя (1.2.4), находим выражение дифференциала производной n–1 — го порядка через параметр t :
.

Интегрируя, получаем выражение производной n-1 — го порядка через параметр t :
(1.2.5) .
Это уравнение, вместе с (1.2.3), дает выражение производной меньшего порядка в параметрическом виде:

Далее выражаем дифференциал производной порядка n – 2 :
.
Подставляя (1.2.4) и (1.2.5), получаем дифференциал, выраженный через параметр t . После чего интегрируем по t , и, вместе с уравнением , получаем выражение производной в параметрическом виде. И так далее, пока получим зависимость функции y от параметра t .

F(x, y (n) ) = 0 Общий случай

Теперь рассмотрим дифференциальное уравнение высшего порядка, содержащее только старшую производную и независимую переменную в общем случае:
(1.3.1) .
Это уравнение можно разрешить в квадратурах, если удастся представить уравнение (1.3.1) в параметрическом виде. То есть если удастся подобрать такие функции , для которых
(1.3.2) ,
и при этом уравнение (1.3.1) окажется эквивалентным уравнениям
(1.3.3) .

Тогда уравнение можно решить в квадратурах. Для этого сначала выразим дифференциал независимой переменной x через параметр t , используя первое уравнение (1.3.3):
.
После этого выражаем через параметр t дифференциал производной n-1-го порядка:
.
Интегрируя это уравнение по переменной t , получаем выражение для производной n-1-го порядка в параметрическом виде:
.
Где .

Далее выражаем через t дифференциал производной n-2-го порядка:
.
Интегрируя, получим параметрическое представление производной n-2-го порядка. И так далее, пока получим параметрическое представление функции y .

F(y (n-1) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-1

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
(2.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(2.1.2) .
Тогда если положить
(2.1.3) ,
то уравнение (2.1.1) будет выполняться автоматически. При этом должно соблюдаться еще одно условие – чтобы представления (2.1.1) и (2.1.3) были эквивалентными. То есть, чтобы при переходе от одного представления к другому, не появились новые и не терялись существующие решения.

Если найдено такое параметрическое представление уравнения (2.1.1), то его можно решить в квадратурах. Для этого, как и в предыдущем случае, сначала выразим дифференциал независимой переменной x через параметр t . Преобразуем первое уравнение (2.1.3):
.
Отсюда
;
(2.1.4) .
Интегрируя, получаем выражение независимой переменной x через параметр t :
(2.1.5) .

Тем же способом, что и в предыдущем случае, выражаем производные и меньших порядков через t :
.
Интегрируем:
.
Продолжая процесс, получаем выражения остальных производных и самой функции y через параметр t . Вместе с уравнением (2.1.5), это дает решение исходного уравнения в параметрическом виде.

y (n-1) = f(y (n) ) Разрешенные относительно младшей производной

Рассмотрим частный случай уравнения (2.1.1), в котором производная меньшего порядка выражена через старшую производную:
.

Это уравнение интегрируется в квадратурах, введением параметра
.
Тогда
.
Из этих уравнений
;
;
;
.

Тем же способом находим выражение через t производных и переменной y .

y (n) = f(y (n-1) ) Разрешенные относительно старшей производной

Рассмотрим второй частный случай, когда старшая производная выражена через производную меньшего порядка:
(2.3.1) .

Если уравнение (2.3.3) удастся разрешить относительно t , то получим зависимость вида . Учитывая (2.3.2), получаем уравнение, в котором производная n–1-го порядка является функцией от независимой переменной:
.
Интегрируя это уравнение n–1 раз, получим зависимость y от x . См. Дифференциальное уравнение y (n) = f(x)

Но в любом случае можно получить решение в параметрическом виде.
;
.

Тем же способом находим выражение через t производных и переменной y .

F(y (n-2) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-2

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
(3.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(3.1.2) .
Положим
(3.1.3) .
Тогда уравнение (3.1.1) выполняется автоматически. Считаем также, что представления (3.1.1) и (3.1.3) эквивалентны.

Для решения уравнения запишем дифференциалы производных порядков n-1 и n-2 :
.
Исключаем dx . Из второго уравнения
(3.1.4) .
Подставим в первое и преобразуем:
;
;
.
Подставляя (3.1.3) и интегрируя, получим выражение производной через параметр t :
;
;
;
.
Знак плюс или минус выбирается из начальных условий, как и постоянная интегрирования .

Из (3.1.4) находим выражение x через t :
(3.1.5) ;
(3.1.6) .

Далее, как и в предыдущих случаях находим выражения производных и зависимой переменной y через t . Например,
;
;
и так далее.

Примечание. В литературе иногда не ставят знак плюс-минус. При этом подразумевают, что корень является многозначной функцией и автоматически может быть как положительным, так и отрицательным.

y (n) = f(y (n-2) ) Разрешенные относительно старшей производной

Сведем к квадратурам уравнение, разрешенное относительно старшей производной:
(3.2.1) .

Для упрощения выкладок введем новую переменную:
(3.2.2) .
Тогда исходное уравнение (3.2.1) станет уравнением второго порядка:
(3.2.3) .
Умножим его на и выделим полную производную:
;
.
Отсюда получаем первый интеграл:
.

Находим выражение для дифференциала . Для этого извлекаем квадратный корень:
.
Отсюда
(3.2.4) .
Знак плюс или минус выбирается из начальных условий. В общем решении допустим любой знак.

Интегрируя, получаем зависимость u от x в неявном виде:
(3.2.5) .
Если после интегрирования удастся разрешить u относительно x , то, поскольку , мы получим уравнение вида (1.1), которое решается последовательным интегрированием.

Если уравнение (3.2.5) разрешить относительно u не удастся, то решаем в параметрическом виде, как это описывалось ранее. То есть вводим параметр . Тогда (3.2.5) и (3.2.4) дают выражения переменной x и ее дифференциала через t :
(3.2.6) .
(3.2.7) .
Далее, уравнение

вместе с (3.2.7) дают параметрическое представление зависимости производной порядка n — 2 от переменной x .

Используя (3.2.6), можно найти параметрическое представление остальных производных и самой функции y от переменной x . Например,
;
.
И так далее.

Примеры решений задач

Все примеры Далее рассматриваются примеры с подробными решениями следующих дифференциальных уравнений.
⇓
⇓
⇓
⇓
⇓

Пример 1

Найти общее решение дифференциального уравнения третьего порядка, содержащего только старшую производную и независимую переменную.
(П1.1) .

По всей видимости, в уравнении (П1.1) выразить через x в элементарных функциях или не возможно, или довольно сложно. Мы не будем пытаться это делать, поскольку здесь независимая переменная x выражена через производную . Поэтому решаем задачу в параметрическом виде.

Вводим параметр t . Получаем параметрические уравнения, эквивалентные (П1.1):
(П1.2) .

Выразим дифференциал переменной x через параметр t :
;
(П1.3) .

Используя (П1.2) и (П1.3), выражаем дифференциал производной второго порядка через параметр t :
.
Интегрируем.
;
(П1.4) .

Используя (П1.3) и (П1.4), аналогично предыдущему имеем:

;

.

Пример 2

Найти частное решение дифференциального уравнения второго порядка, содержащее только вторую производную и независимую переменную:
(П2.1) ;
(П2.2) .

Это уравнение является кубическим по отношению ко второй производной , и уравнением седьмой степени (если умножить его на x ) по отношению к независимой переменной x . Можно попытаться разрешить его относительно или x , но здесь есть более простой способ.

Заметим, что уравнение (П2.1) выполняется, если выразить зависимость от x , определяемую уравнением (П2.1) в параметрическом виде:
(П2.3) .
Действительно, подставляя (П2.3) в (П2.1) получаем:
;
;
.
То есть если взять параметрическое представление (П2.3), то уравнение (П2.1) выполняется.

Однако это не означает, что представление (П2.3) автоматически эквивалентно уравнению (П2.1). Поскольку кубическое уравнение может иметь три действительных корня, то, возможно, уравнение (П2.3) можно представить в параметрическом виде тремя неэквивалентными способами. Также возможен случай, когда условия теоремы существования и единственности решения дифференциального уравнения не выполняются, и заданным начальным условиям будут удовлетворять несколько решений. Все это нужно иметь в виду при решении подобных уравнений. Но нам нужно найти любое решение, удовлетворяющее заданным начальным условиям. Поэтому попробуем применить для этой цели представление (П2.3).

Выразим дифференциал независимой переменной x через дифференциал параметра t , используя (П2.3):
.
Выразим дифференциал производной через параметр t и его дифференциал:
.
Интегрируем:
. Найдем значение постоянной , используя первое начальное условие (П2.2). Из (П2.3) находим: . При . При . Отсюда .

Итак, мы нашли параметрическое представление для производной:
.
Аналогично предыдущему, выражаем y через параметр t :
;

.
Находим значение постоянной , используя второе начальное условие (П2.2). При . При . Отсюда .

Тем самым мы нашли частное решение в параметрическом виде:
.
Выразим t через x .
;
.

Пример 3

Решить дифференциальное уравнение, содержащее только производные первого и второго порядков:
(П3.1) .

Нетрудно видеть, что если положить
(П3.2) ,
то уравнение (П3.1) выполняется автоматически. Поэтому решаем это уравнение в параметрическом виде.

Выразим дифференциал независимой переменной x через параметр t .
;
;
(П3.3) .

Интегрируя (П3.3), получаем выражение независимой переменной x через параметр t :
;
(П3.4) .

Используя формулу , и применяя выражение через t (см. (П3.2)), выразим дифференциал dy через t :
.

Интегрируя, находим выражение зависимой переменной через параметр t :
.

Итак, мы нашли зависимость в параметрической форме:
.
Отсюда можно получить зависимость y от x в явном виде. Из второго уравнения, . Подставляем в первое:
.

Пример 4

Решить дифференциальное уравнение, содержащее только производные второго и третьего порядков:
(П4.1) .

Это дифференциальное уравнение содержит только производные второго и третьего порядков. При этом оно разрешено относительно высшей производной. Решаем параметрическим методом. За параметр t возьмем производную второго порядка:
(П4.2) .

Выразим дифференциал независимой переменной x через параметр t . Из (П4.1) имеем:
;
;
(П4.3) .

Выразим независимую переменную x через параметр t . Для этого интегрируем (П4.3):
;
(П4.4) .
См. Обратные гиперболические функции, их графики и формулы

Выразим дифференциал через параметр t и, интегрируя, выразим производную через t :
;
;
(П4.5) .

Выразим дифференциал зависимой переменной y через параметр t . После чего интегрируя, выразим y через t :
;
;
(П4.6) .

Исключим параметр t из уравнений (П4.4) т (П4.6).
;
.

Примечание.
Эту задачу можно решить проще, если с самого начала выбрать следующее параметрическое представление для производных:
.

Пример 5

Решить дифференциальное уравнение с заданными начальными условиями:
(П5.1) ;
(П5.2) .

Уравнение имеет вид (3.2.3). В нем вторая производная выражена через функцию (зависимую переменную y ). Решаем изложенным выше методом ⇑.

Умножим исходное уравнение (П5.1) на и выделяем полный дифференциал.
;
;
;
.
Извлекаем квадратный корень:
(П5.3) .

Найдем значение постоянной и знак корня из начальных условий (П5.2). Для этого подставляем в (П5.3) :
.
Отсюда видно, что нужно взять знак плюс и . Тогда
.

Разделяем переменные и интегрируем.
;
;
;
(П5.4) .

Определяем значение постоянной . Для этого подставляем значения начальных условий (П5.2): :
.
Отсюда . Подставляем в (П5.4):
.

Возводим в квадрат и выполняем преобразования:
;
.
Извлекаем квадратный корень:
.
Выбираем знак плюс или минус из начальных условий (П5.2). Подставляем :
.
Этому уравнению удовлетворяет знак плюс. Тогда
.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 11-05-2021

Некоторые виды уравнений, интегрируемых в квадратурах

По этой ссылке вы найдёте полный курс лекций по математике:

общем случае, даже зная, что решение уравнения существует, отыскать его довольно трудно. Однако существуют некоторые виды дифференциальных уравнений, методы получения решений которых особенно просты (при помощи интегралов от элементарных функций). Рассмотрим некоторые из них. 5.1. Уравнения с разделяющимися переменными Уравнение вида называется дифференциальным уравнением с разделенными переменными. Здесь f\(y), /2 (я) — известные непрерывные функции своих аргументов.

Покажем, как найти решение этого уравнения. Пусть F\(y) и F2(x) — первообразные функции f\(y) и /2(2) соответственно. Равенство (1) равносильно тому, что дифференциалы этих функций должны совпадать Отсюда следует, что где С — произвольная постоянная. Разрешая последнее уравнение (2) относительно у, получим функцию (может быть, и не одну) которая обращает уравнение (1) в тождество и значит, является его решением Например, — уравнение с разделенными переменными.

Записав его в виде и интегрируя обе части, найдем общий интеграл данного уравнения: Уравнение вида в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от х и только от уу называется дифференциальным уравнением с разделяющимися переменными, так как путем деления на 4>\(y)fi(x) £ 0 оно приводится к уравнению с разделенными переменными Пример 1.

Проинтегрировать уравнение Некоторые виды уравнений, интегрируемых в квадратурах Уравнения с разделяющимися переменными Уравнения, однородные относительно х и у Линейные дифференциальные уравнения Уравнение Бернулли Уравнения в полных дифференциалах Деля обе части уравнения на , приведем его к виду Интегрируя обе части полученного равенства, найдем откуда Заметим, что деление на может привести к потере решений, обращающих в нуль произведение .

Например, разделяя переменные в уравнении получаем а после интегрирования — откуда (здесь С может принимать как положительные, так и отрицательные значения, но С Ф 0). При делении на у потеряно решение которое может быть включено в общее решение у = Сх, если постоянной С разрешить принимать значение С = 0. Если считать переменные х и у равноправными, то уравнение теряющее смысл при х = 0, надо дополнить уравнением которое имеет очевидное решение х = 0. где /j (ж, у) = у^у, используя уравнение (4′) там, где уравнение (4) не имеет смысла, а уравнение (4′) имеет смысл.

Некоторые дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. Например, уравнение вида где f(z) — непрерывная функция своего аргумента, а, Ь, с — постоянные числа, подстановкой z = ах + by + с преобразуется в дифференциальное уравнение с разделяющимися переменными: откуда После интегрирования получаем Заменяя в последнем соотношении найдем общий интеграл уравнения (5). Пример 2.

Проинтегрировать уравнение В общем случае наряду с дифференциальным уравнением следует рассматривать уравнение 4 Положим z = x + y, тогда откуда Интегрируя, находим или Подставляя вместо z величину х + у, получаем общее решение данного уравнения Пример 3. Известно, что скорость радиоактивного распада пропорциональна количеству х еще не распавшегося вещества. Найти зависимость х от времени t, если в начальный момент t = to имелось х = х0 вещества.

Дифференциальное уравнение процесса dx Здесь к > 0 — постоянная распада — предполагается известной, знак указывает на уменьшение х при возрастании t. Разделяя переменные в уравнении и интегрируя, получаем откуда х = Се

и. Учитывая начальное условие = xq, находим, что С — х0ек1с, поэтому Любой процесс (не только радиоактивный распад), при котором скорость распада пропорциональна количеству еще не прореагировавшего вещества, описывается уравнением (*).

Уравнение отличающееся лишь знаком правой части от уравнения (*), описывает лавинообразный процесс размножения, например «размножение» нейтронов в цепных ядерных реакциях или размножение бактерий в предположении, что скорость их размножения пропорциональна наличному числу бактерий. Решение уравнения , удовлетворяющее условию имеет вид и в отличие от решения уравнения ) возрастает с возрастанием t.

Уравнения можно объединить в одно которое дает простейшую математическую модель динамики популяций (совокупности особей того или иного вида растительных или животных Организмов). Пусть y(t) — число членов популяции в момент времени t. Если предположить, что скорость изменения популяции пропорциональна величине популяции, то мы приходим к уравнению . Положим к —т — я, где m — коэффициент относительной скорости рождаемости, an — коэффициент относительной скорости умирания.

Тогда к > 0 при п и к при тп. Если в момент t = О величина популяции равна уо, то уравнение приводит к экспоненциальному закону изменения популяции Предположение, что величины шип являются постоянными, не выполняется для больших популяций. Действительно, большое число членов популяции приводит к уменьшению соответствующих ресурсов, что снижает скорость рождаемости и увеличивает скорость умирания. Это можно задать простейшими законами положительные постоянные.

Возможно вам будут полезны данные страницы:

Тогда Уравнение динамики популяции в этой модели имеет вид Это так называемое логистическое уравнение — фундаментальное уравнение в демографии и в математической теории экологии. Оно применяется в математической теории распространения слухов, болезней и других проблемах физиологии и социологии. Разделяя переменные в последнем уравнении, получаем откуда и далее .

Потенцируя Некоторые виды уравнений, интегрируемых в квадратурах Уравнения с разделяющимися переменными Уравнения, однородные относительно х и у Линейные дифференциальные уравнения Уравнение Бернулли Уравнения в полных дифференциалах и выражая у через t, окончательно получаем Считая, , найдем уравнение логистической кривой При получаем, что Логистическая кривая содержит два параметра Л и а. Для их определения надо иметь два дополнительных значения y(t) при каких-то 5.2.

Уравнения, однородные относительно х и у Функция f(x, у) называется однородной функцией п-го измерения относительно переменных х иу, если при любом допустимом t справедливо тождество .

Например, для функции так что однородная функция относительно переменных х и у второго измерения. Для функции имеем есть однородная функция нулевого измерения. Дифференциальное уравнение первого порядка называется однородным относительно х и у, если функция f(x, у) есть однородная функция нулевого измерения относительно переменных х и у.

Пусть имеем дифференциальное уравнение однородное относительно переменных хну. Положив t = ^ в тождестве получим т. е. однородная функция нулевого измерения зависит только от отношения аргументов. Обозначая / (I, |) через (*), видим, что однородное относительно переменных ж и у дифференциальное уравнение всегда можно представить в виде При произвольной непрерывной функции переменные не разделяются. Введем новую искомую функцию u(z) формулой и = J, откуда у = хи.

Подставляя выражение ^ = и 4- в уравнение (6), получаем Деля обе части последнего равенства на и интегрируя, находим Заменяя здесь и на его значение \, получаем общий интеграл уравнения (6). Пример 4. Проинтегрировать уравнение Положим уравнение преобразуется к виду Интегрируя, найдем или Пример 5. Найти форму зеркала, собирающего пучок параллельно падающих на него лучей в одну точку.

Прежде всего, зеркало должно иметь форму поверхности вращения, так как только для поверхности вращения все нормали к поверхности проходят через ось вращения. Выберем прямоугольную декартову систему координат так, чтобы лучи были параллельны оси Ох и чтобы точкой, в которой собирались бы отраженные лучи, явилось бы начало координат. Найдем форму сечения зеркала плоскостью хОу. Пусть уравнение сечения есть ) (рис.6).

В точке Af(x,y) падения луча L на зеркало проведем касательную BN к сечению и обозначим ее угол с осью Ох через а. Пусть N — точка пересечения этой касательной с осью Ох. По закону отражения углы NMO и BML равны. Нетрудно видеть, что угол МОР равен 2а. Так как tga = у , tg2a = J то во всякой точке кривой у — ip(x) выполняется соотношение — дифференциальное уравнение, определяющее требуемый ход луча. Разрешая это уравнение относительно производной, получаем два однородных уравнения:

Первое из них путем замены | = и преобразуется к виду — произвольная постоянная. Решение неоднородного уравнения (10) ищем в виде — новая неизвестная функция. Вычисляя производную и подставляя значения и у в исходное уравнение (10), получаем dx откуда — новая произвольная постоянная интегрирования. Следовательно, Это есть общее решение линейного неоднородного дифференциального уравнения (10).

В формуле (14) общего решения неопределенные интегралы можно заменить определенными интегралами с переменным верхним пределом: Здесь С = у(жо) = уо, поэтому общее решение уравнения (10) можно записать в виде (15) где роль произвольной постоянной играет начальное значение уо искомой функции у (ж). Формула (15) является общим решением уравнения (10) в форме Коши.

Отсюда следует, что если р(х) и q(x) определены и непрерывны в интервале то и решение у(х) уравнения (10) с любыми начальными данными у(ж0) = уо будет непрерывным и даже непрерывно дифференцируемым при всех конечных значениях ж, так что интегральная кривая, проходящая через любую точку (жо, уо), будет гладкой кривой в интервале Поэтому сначала интегрируем соответствующее однородное уравнение общее решение которого имеет вид Пример б.

Проинтегрировать уравнение Ч Однородное уравнение соответствующее данному, проинтегрируем, разделяя переменные: Решение исходного уравнения будем искать в виде где С(х) — неизвестная функция. Находя ^ и подставляя , последовательно получаем: где С — постоянная интегрирования. Из формулы находим общее решение уравнения Частное решение неоднородного уравнения легко усматривается. Вообще, если удается «угадать» частное решение линейного неоднородного уравнения, то разыскание его общего решения значительно упрощается. Пример 7.

Рассмотрим дифференциальное уравнение, описывающее изменение силы тока при замыкании цепи постоянного электрического тока. 4 Если R — сопротивление цепи, Е — внешняя ЭДС, то сила тока / = /(f) постепенно возрастает от значения, равного нулю, до конечного стационарного значения ^. Пусть L — коэффициент самоиндукции цепи, роль которой такова, что при всяком изменении си- лы тока в цепи появляется электродвижущая сила, равная L-^ и направленная противоположно внешней ЭДС.

На основании закона Ома, по которому в каждый момент t произведение силы тока на сопротивление равно фактически действующей ЭДС, получаем ) Уравнение (*) есть линейное неоднородное уравнение относительно I(t). Нетрудно видеть, что его частным решением является функция Общее решение соответствующего однородного уравнения откуда общее решение неоднородного уравнения («):

При t = 0 имеем , поэтому так что окончательно Отсюда видно, что сила тока при включении асимптотически приближается при к своему стационарному значению ожет быть проинтефировано также следующим приемом. Будем искать решение у(х) уравнения (10) в виде Линейное неоднородное дифференциальное уравнение где и<х) и v(x) — неизвестные функции, одна из которых, например v(x), может быть выбрана произвольно.

(10), после элементарных преобразований получим Выберем в качестве v(ar) любое частное решение v(«) ^ 0 уравнения Тогда в силу (17) для и(ж) получим уравнение которое без труда интегрируется в квадратурах. Зная v(x) и и(х), найдем решение у(х) уравнения (10). Пример. Найти общее решение уравнения Будем искать решение у(х) данного линейного неоднородного уравнения в виде Подставляя исходное уравнение, получим.

Определим функцию v(x) как решение уравнения Разделяя переменные, найдем Выберем любое частое решение, например, отвечающее ) получим Для общего решения исходного уравнения получаем выражение Преимущество метода вариации постоянной заключается в том, что он переносится на линейные неоднородные дифференциальные уравнения высшего порядка. Уравнение Бернулли Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным.

К числу таких уравнений относится уравнение Бернуми Уравнение это предложено Я. Бернулли в 1695 г., метод решения опубликовал И. Бернулли в 1697 г. При а = 1 получаем однородное линейное уравнение При а = 0 — неоднородное линейное уравнение Поэтому будем предполагать, что (для а нецелого считаем, что у > 0). Подстановкой z = y_a+1 уравнение Бернулли приводится к линейному уравнению относительно функции z(x). Однако уравнение Бернулли можно проинтегрировать сразу методом вариации постоянной.

Это делается так. Сначала интегрируем уравнение Его общее решение Решение уравнения Бернулли будем искать в виде где С(х) — новая неизвестная функция. Подставляя это выражение для у(х) в уравнение Бернулли, получаем — уравнение с разделяющимися переменными относительно С(х). Интегрируя это уравнение, находим где С — постоянная интегрирования. Тогда из формулы получаем обший интеграл уравнения Бернулли Замечание.

При а > 0 уравнение Бернулли имеет очевидное решение у = 0. Для интегрирования уравнения Бернулли можно также воспользоваться подстановкой Некоторые виды уравнений, интегрируемых в квадратурах Уравнения с разделяющимися переменными Уравнения, однородные относительно х и у Линейные дифференциальные уравнения Уравнение Бернулли Уравнения в полных дифференциалах где в качестве берется любое нетривиальное решение уравнения а функция и(ж) определяется как решение уравнения Пример.

Найти решение уравнения Бернулли Ищем решение у(х) уравнения в виде Подставляя исходное уравнение, получим . Выберем в качестве v(x) какое-нибудь ненулевое решение уравнения и проинтегрируем его, Поскольку нас интересует какое угодно частное решение, положим . возьмем v = Тогда для и(х) получим уравнение интегрируя которое, найдем Общее решение у(х) исходного уравнения определится формулой 5.5.

Уравнения в полных дифференциалах Уравнение называется уравнением в полных дифференциалах, если левая часть уравнения представляет собой полный дифференциал некоторой функции гх(ж, у) двух независимых переменных ж и у, т. е. В этом случае «(ж, у) — С будет общим интегралом дифференциального уравнения (18). Будем предполагать, что функции М(ж, у) и N(x, у) имеют непрерывные частные производные соответственно по у и по ж в некоторой односвязной области D на плоскости хОу. Теорема 4.

Для того чтобы левая часть М(ж, у) dx + N(xt у) dy уравнения (18) была полным дифференциалом некоторой функции и(х, у) двух независимых переменных х и у, необходимо и достаточно, чтобы выполнялось тождество 4 Необходимость. Предположим, что левая часть уравнения (18) есть полный дифференциал некоторой функции Дифференцируем первое соотношение по у, а второе по х: ду вудх дх дхду Отсюда, в силу равенства смешанных производных, вытекает тождество Необходимость (19) доказана.

Достаточность. Покажем, что условие (19) является и достаточным, а именно, предполагая его выполненным, найдем функцию tx(x, у) такую, что или, что то же, Найдем сначала функцию и(ху у), удовлетворяющую первому условию (20). Интегрируя это равенство по х (считаем у постоянной), получаем где произвольная функция от у. Подберем так, чтобы частная производная по у от функции и, определяемой формулой (21), была равна N(x> у). Такой выбор функции (р(у) при условии (19) всегда возможен.

В самом деле, из (21) имеем Приравняв правую часть полученного равенства к N(x, у), найдем Левая часть последнего равенства не зависит от х. Убедимся в том, что при условии (20) в его правую часть также не входит х. Для этого покажем, что частная производная по х от правой части (22) тождественно равна нулю. Имеем Теперь, интегрируя равенство (22) по у, получим, что где С — постоянная интегрирования.

Подставляя найденное значение для в формулу (21), получим искомую функцию полный дифференциал которой, как нетрудно проверить, равен Приведенный прием построения функции м(х, у) составляет метод интегрирования уравнения (18), левая часть которого есть полный дифференциал. Пример 8. Проверить, что уравнение является уравнением в полных дифференциалах, и проинтегрировать его. А В данном случае откуда Следовательно, уравнение есть уравнение в полных дифференциалах.

Теперь находим и или Находя от функции и из и приравнивая ^ функции , получаем следовательно, Подставив найденное выражение для , найдем Таким образом, — общий интеграл исходного уравнения. Иногда можно найти такую функцию , что будет полным дифференциалом, хотя М dx + N dy может им и не быть. Такую функцию у) называют интегрирующим множителем.

Можно показать, что для уравнения первого порядка при определенных условиях на функции М(х, у) и N(x, у) интегрирующий множитель всегда существует, но отыскание его из условия в общем случае сводится к интегрированию уравнения в частных производных, что составляет, как правило, задачу еще более трудную. Задача. Найти интегрирующий множитель для линейного дифференциального уравнения dy Указание. Искать множитель в виде ц = ц(х).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y ‘(x), y »(x), … , y ( n ) (x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y ( n ) = f(x, y, y ‘, y », … , y ( n − 1) ).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀, y ‘(x₀) = y₁, y »(x₀) = y₂, … , y (n − 1) (x₀) = y_{n − 1}.

Общим решением дифференциального уравнения F(x, y(x), y ‘(x), y »(x), … , y ( n ) (x)) = 0 называется функция y = Ф(x, С₁, С₂, … , С_n), содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁, С₂, . С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y ( n ) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида Заменой z(x) = y (k) (x) такое уравнение сводится к уравнению (n−k)–го порядка: Если z = z(x,C₁. C_n-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле

Простейшее уравнение, допускающее понижение порядка — уравнение вида y (n) = f (x), его общее решение имеет вид

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной — уравнения вида F( y , y‘, . y (n) ) = 0. Порядок уравнения можно понизить заменив y ‘ = p ( y ). После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p ( y ) будет на единицу меньше, чем порядок старшей производной от y ( x ) в исходном уравнении.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции — уравнения вида F( x , y‘, . y (n) ) = 0. Порядок уравнения можно понизить заменив y ‘ = p ( x ). После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение: F( x , p , p ‘, . p (n — 1) ) = 0. Если правая часть уравнения F(x, y, y ‘. y ( n ) ) = 0, удовлетворяет условию однородностиF(x, ty, ty ‘. ty ( n ) ) = t k F(x, y, y ‘. y ( n ) ) то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y ( n ) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой Выражение для первой производной от y(x) не содержит производной от z(x): . Поэтому, заменив в исходном уравнении y, y ‘. y ( n ) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл.

Совокупность соотношений вида:

Где y₁, y₂, …, y_n искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка.

Будем предполагать функции F₂, F₂, …, F_n такими, что система разрешима относительно производных от искомых функций:

Такие системы называются нормальными системами дифференциальных уравнений.

Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Семейство решений системы (2), зависящее от n произвольных постоянных C₁, C₂, …, C_n

называют обычно общим решением этой системы.

Дадим определение общего решения системы (2) в области Dизменения переменных x, y₁, y₂, …, y_n.

В качестве области D будем рассматривать область в пространстве (x, y₁, y₂, …, y_n), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2).

Совокупность n функций (6), определённых в некоторой области изменения переменных x, C₁, C₂, …, C_n, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C₁, C₂, …, C_n в области D, так что при любых значениях x, y₁, y₂, …, y_n, принадлежащих области D, системой (6) определяются значения C₁, C₂, …, C_n:

и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C₁, C₂, …, C_n, доставляемых формулами (7), когда точка (x, y₁, y₂, …, y_n) пробегает область D.

Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C₁, C₂, …, C_n,, включая бесконечности, будет частным решением.

Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение.

1-ое определение интеграла системы. Функция φ(x, y₁, y₂, …, y_n), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y₁, …, y_n любым частным решением этой системы она обращается в постоянную.

2-ое определение интеграла системы. Функция φ(x, y₁, y₂, …, y_n), имеющая непрерывные частные производные по x, y₂, …, y_n, и такая, что в рассматриваемой области не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:

.

Равенство , где – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).

Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y₁, y₂, …, y_n, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.019 сек.)