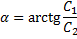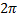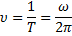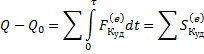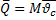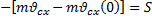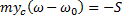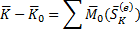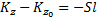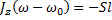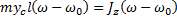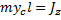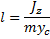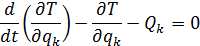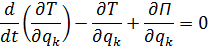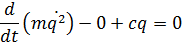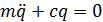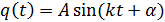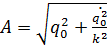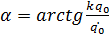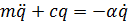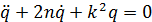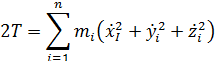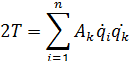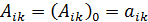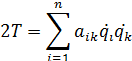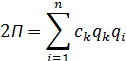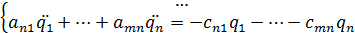Дифференциальные уравнения колебаний с одной степенью свободы

Дифференциальные уравнения колебаний с одной степенью свободы

1) Свободные колебания системы с одной степенью свободы. Интегрирование дифференциального уравнения движения системы.

Колебательное движение механической системы — такое движени, при котором все ее обобщенные координаты или хотя бы одна из них изменяется с неоднократным возрастанием и убыванием.

Свободные колебания системы с одной степенью свободы.

Свободные колебания (собственные колебания) — колебания в любой колебательной системе, происходящие в отсутствие внешнего воздействия.

Дифференциальное уравнение свободных колебаний системы с одной степенью свободы:

, где a>0; b0; c>0.

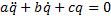
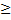
а — обобщенный коэффициент инерции; b — обобщенный коэффициент сопротивления; с — обобщенный коэффициент жесткости.

В случае если система консервативная, т.е. b=0, дифференциальное уравнение движения принимает форму:

, где — круговая или циклическая частота.

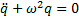
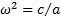
Запишем дифференциальное уравнение в виде:

.

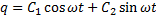
C₁ и C₂ — произвольные постоянные, которые мы определим из начальных условий: при t=0 q=q₀, .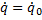

Отсюда C₁=q₀; .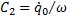

Введем новые произвольные постоянные:

;

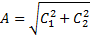
и представим решение дифференциального уравнения в амплитудной форме:

.

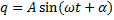
Амплитуда (А) — наибольшее отклонение какой либо точки тела, совершающего колебания, от положения равновесия.

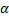
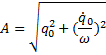
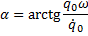
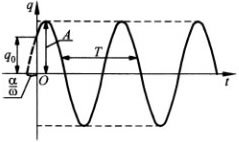
Произвольные постоянные А и выражаются через начальные условия следующим образом:

; .

Зависимость q(t) представлена на рисунке.

Гармонические колебания — колебания, при которых обобщенная координата изменяется во времени по закону синуса или косинуса.

Свободные колебания с одной степенью свободы являются гармоническими.

Характеристики гармонических колебаний:

— круговая, или циклическая частота, измеряемая в секундах в минус первой степени;

— фаза колебаний;

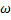
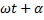
Фаза колебаний — физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени, или проще: аргумент синуса.

— начальная фаза колебаний;

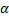
А — амплитуда колебаний;

Т — период колебаний — время в секундах. за которое фаза колебаний изменится на

.

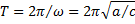
В инженерной практике используют величину, обратную периоду колебаний, называемую частотой колебаний

и измеряемую в герцах (Гц).

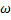
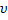
Круговая частота , период колебаний Т и частота не зависят от начальных условий, поэтому их называют собственными характеристиками колебательной системы.

Свойство независимости частоты и периода колебаний от начальных условий — свойство изохронности колебаний — связано с линейностью дифференциального уравнения и, следовательно, с допущением о малости колебаний.

2) Центр удара. Условие отсутствия ударных реакций в опорах вращающегося тела.

Удар — механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

Центр удара — точка, в которой приложен импульс 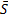при отстутствии ударных реакций подшипников.

Импульс силы (количество движения) — векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.

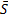
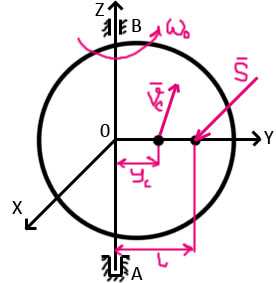
Для того, чтобы ударные реакции в опорах отсутствовали необходимо, чтобы импульс был перпендикулярен оси вращения тела Oz.

Рассмотрим тело вращающееся вокруг оси z.

Воспользуемся теоремой об изменении количества движения:

В проекции на ось Х:

Воспользуемся теоремой об изменение кинетического момента:

Если центр масс тела находится на оси вращения, то центр удара отсутсвует.

Итак, чтобы при приложении к телу, вращающемуся вокруг неподвижной оси, ударного импулься не возникали ударные реакции в опорах, т.е. чтобы существовал центр удара, необходимо и достаточно выполнить следующие условия:

1) ударный импульс должен быть перпендикулярен плоскости, проходящей через ось вращения тела и его центр масс;

2) точка пересечения линии действия ударного импульса с плоскостью, проходящей через ось вращения тела и его центр масс, должна лежать в этой плоскости по одну сторону от оси вращения вместе с центром масс;

3) ударный импульс, произвольной по величине, должен лежать в плоскости, перпендикулярной оси вращения и проходящей через точку О, для которой ось вращения является главной осью инерции тела.

Колебания системы с одной степенью свободы

Колебания системы с одной степенью свободы

• Механическая система с одной степенью свободы имеет одну обобщенную координату q, и ее движение описывается одним уравнением Лагранжа ди дк дк (1). Обобщенная сила Q может рассматриваться как состоящая из трех частей: Q = Qn + Q ‘+ QB, где Qn — обобщенная сила потенциальных сил. Потенциальная энергия в общем случае зависит от координат точки системы, поэтому она зависит от обобщенной координаты q и обобщается по формуле Qn = —dP / dq Оно не зависит от скорости q.

В случае нестационарного силового поля и нестационарного силового поля потенциальная энергия явно зависит от времени. 0F включает в себя обобщенную часть силы, которая является результатом действия сопротивления. Сила сопротивления зависит как от числового значения, так и от направления скорости системной точки. Далее рассматривается случай линейного сопротивления, когда сопротивление системных точек пропорционально скорости этих точек и направлено в противоположном направлении. Часть обобщенной силы QB является производной от так называемых вынужденных или возмущающих сил, которые в основном зависят от времени.

Поступательная часть перемещения тела зависит от выбора точки, вместе с которой перемещается тело, а вращательная часть перемещения вокруг оси или вокруг точки не зависит от выбора точки. Людмила Фирмаль

Далее рассмотрим случай гармонических возмущений, где Q изменяется во времени в соответствии с законом синуса. В общем случае зависимость QB от времени может быть расширена с помощью ряда Фурье для учета дифференциальных уравнений движения для каждого синусоидального члена. Естественная линейная вибрация системы Под действием нескольких потенциальных сил, то есть b = -dlJ / dq, рассмотрим небольшую вибрацию системы с одной степенью свободы. Сопротивление и возмущение Там нет власти. Такая вибрация называется внутренней или свободной.

Когда система движется, обобщенные координаты, скорость и ускорение достаточно малы, чтобы игнорировать все члены q, q и q, которые являются квадратичными или более высокими в терминах уравнения Лагранжа (1), то есть, члены, которые включают эти квадраты Если система имеет малую вибрацию, то для обобщенной координаты q получается линейное дифференциальное уравнение. Колебания, в которых дифференциальное уравнение является линейным, называются линейными. Небольшие колебания линейны. Однако линейность не обязательно является небольшой вибрацией.

В общем, ограничения, которые должны быть наложены на величину, характеризующую движение, чтобы вибрация была уменьшена, могут быть установлены только после того, как проблема будет полностью решена в предположении, что вибрация мала. Далее рассматриваются только небольшие колебания или, если не маленькие, линейные колебания. Дифференциальное уравнение для естественной линейной вибрации системы. Чтобы вывести линейное уравнение малых собственных колебаний из уравнения Лагранжа (1), кинетическая и потенциальная энергии должны быть последовательно растянуты вблизи положения равновесия системы с q = 0.

Рассмотрим систему, в которой голономная, идеальная, неосвобожденная и фиксированная связь состоит из N точек и движется около положения равновесия. Ее кинетическая энергия При сделанных предположениях о совместной стационарности радиус-вектор r * каждой точки в системе зависит от времени только через обобщенную координату q. Следовательно, rk = — ^ q. Подстановка этого gk в уравнение кинетической энергии дает r = 72l ^ 2. Как и в случае с gk, величина A может зависеть только от q, а не от q. Когда A (q) расширяется вблизи q = 0 степенного ряда, Далее индекс 0 означает, что соответствующее значение вычисляется с q = 0.

Чтобы получить кинетическую энергию в терминах квадратичного и более низкого членов для q и q, достаточно получить только постоянное значение Ao из разложения A (. Где q0 и q0 — начальные значения обобщенных координат и обобщенной скорости. Используйте выражения q и q с r = 0, чтобы получить Ci = Людмила Фирмаль

Обратите внимание на основные характеристики естественной линейной вибрации. Рисунок 111 Амплитуда этих собственных линейных колебаний системы является гармонической величиной постоянной вибрации И определяется начальными условиями. Период колебаний также является постоянным значением и не зависит от амплитуды и, следовательно, начальных условий. Величина периода является характеристикой системы вибрации, т.е. Он определяется только коэффициентом инерции а и жесткостью с. Независимость периода вибрации от амплитуды называется виброизохронизмом. Уникальная линейная вибрация.

При отсутствии возмущающих сил они могут возникать только при начальных условиях, которые не равны нулю. То есть в первый момент система имеет ненулевую начальную обобщенную координату q0 или начальную обобщенную скорость q0. Гармоническое колебание точки при наличии линейной восстанавливающей силы вызвано начальным отклонением точки x0, начальной скоростью a0 или обоими. Гармоническая вибрация имеет характеристику, заключающуюся в том, что, как только она возникает в определенной точке, она продолжается до тех пор, пока не произойдет изменение параметров вибрации, если не будет другого влияния.

Однако обычно вибрация всегда сопровождает сопротивление, и природа естественной вибрации меняется. В дополнение к графику колебаний его колебательное движение может быть представлено на фазовой плоскости — плоскости переменных q и q, называемых фазовыми переменными. Для точечных колебаний фазовыми переменными являются x и v = x. Давайте создадим фазовый портрет гармонической вибрации точки. У нас есть x — грех (£ f + a); v = x = Akcos (kt + v). Рисунок 112 Удалите время t из этих уравнений, чтобы получить эллиптическое семейство в фазовой плоскости (x, p). Эти кривые (рис. 112), в зависимости от параметра A, называются фазовыми траекториями.

Семейство фазовых траекторий зависит от следующих амплитуд: Вариация определяется начальными условиями. Каждая фазовая траектория соответствует паре начальных значений x0 и v0. Точка равновесия на фазовой плоскости соответствует началу координат x = 0, a = 0. Когда точка массы гармонично колеблется, ее координата x и скорость v изменяются со временем. В результате каждый момент на фазовой плоскости соответствует определенной позиции точки изображения с координатами x и V. В течение одного полного гармонического колебания (периода) точка изображения представляет эллипс на фазовой плоскости. Отметим, что замкнутые фазовые траектории соответствуют периодическим колебаниям на фазовой плоскости и наоборот.

Тип фазовой траектории характеризует устойчивость или неустойчивость положения равновесия и малость вибрации. Консервативные системные фазовые траектории могут быть построены с использованием интеграции энергии. Каждая фазовая траектория соответствует определенному значению полной механической энергии. Если дифференциальное уравнение для колебательного движения является нелинейным, изучение движения с использованием фазовых траекторий является одним из наиболее часто используемых методов. mx = —cx \ x + fc2x = 0; k = ^ / s! т. Если вы не выберете место статического равновесия в контрольной точке, уравнение будет иметь постоянную правую часть. Другими словами, это становится неравномерным.

Решение дифференциального уравнения может быть выражено в следующем виде: x = C1cos * / + C2sin * (; ”= x = −C, * -sinfc (+ C2 * cosb. Константы C и C2 определяются начальными условиями. Время 1 = 0, начальная скорость x = b0 = 10 см / с; х = х0 = х0-х „= 8-5 = 3 см; k = y / eim = y / glkcl = y / 99OI5 = 14 с «’ Константа С ‘! И с2. Если выражение для x и x равно 1 = 0, значение равно C | = xo = 3cm. C2 = »o / * = 0,71 см Уравнение движения груза принимает вид x = 3cos 141 + 0,71 sin 141 см Используйте формат амплитуды. амплитудное 4 = х / с? + C? =, / 9 + 0,50 х 3,08 см.

Начальная фаза а. sin a = C, l = 0,97> 0; cos a = C2 / A = 0,71 / A> 0. Следовательно, угол a находится в первой четверти и, в зависимости от значения (например, sina), a = 1,34 = 0,43 л. Уравнение движения для нагрузки в амплитудной форме имеет вид ,

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение Лагранжа. Свободные колебания системы с одной степенью свободы (начальные условия, уравнения, определения). Свободные колебания системы при сопротивлении

Для исследования колебательных систем с конечным числом степеней свободы используются уравнения Лагранжа в обобщенных координатах, составленные в предположении о том, что связи, наложенные на систему, идеальны; уравнения не содержат реакций связей; входящие в уравнения величины, определяющие движения системы, непосредственно связаны обобщенными силами.

Для консервативных систем уравнение Лагранжа записывается через потенциальную энергию:

В этом случае энергия характеризует полную механическую энергию системы.

Колебания системы с одной степенью свободы.

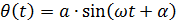
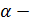
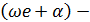
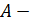
Система с одной СС – система, положение которой в пространстве однозначно определяется заданием одной обобщенной координаты. Например математический маятник движется по закону , где начальная фаза, фаза колебаний, амплитуда.

Уравнения малых свободных колебаний системы с одной СС.

Колебания называются свободными, если скорость изменения состояния системы определяется только состоянием самой системы. Такая система – линейный осциллятор.

Система консервативна, уравнение Лагранжа:

Сопротивление среды равно нулю, поэтому

Потенциальная энергия оценивается через жесткость системы: /

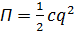
Общее решение: .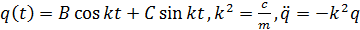

Подстановка для решения: , ,

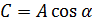
Начальные условия для решения: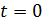

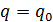
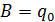
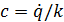
Свободные колебания при наличии сопротивления.

В этом случае на систему действует сила :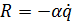

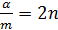
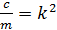
Введем отношение , тогда

Колебания системы с конечным числом степеней свободы, приведенная система. Кинетическая и потенциальная энергия малых свободных колебаний. Уравнение малых колебаний системы около положения устойчивого равновесия.

Детали или механизмы системы на практике являются сложной упругой системой с бесконечным числом степеней свободы. Для определения положения точек при колебаниях в любой момент времени необходимо найти функцию времени и координат точек. При расчетах упругая система заменяется более простой системой с конечным числом степеней свободы – приведенная система.

Кинематическая энергия системы с 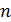степеней свободы:

Если выполняется переход к обобщенным координатам:

инерционные коэффициенты.

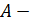
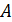
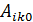
Для колебаний возле положения устойчивого равновесия разложение коэффициентов в ряд по степеням ограничивается рассмотрением постоянного коэффициента , остальные же не рассматриваются ввиду их малости.

Потенциальная энергия системы может быть выражена через упругие коэффициенты:

Уравнения малых колебаний системы около положения устойчивого равновесия.

Подставляя в уравнение Лагранжа выражения для кинетической и потенциальной энергий b принимая, что: 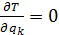, можно получить систему дифференциальных уравнений, описывающих колебания системы:

Общее решение данной системы уравнений определяет колебания механической системы.