Дифференциальные уравнения математические модели физических процессов

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ

ВВЕДЕНИЕ

Исследование поведения различных систем (сопротивления материалов, динамики, биологии, химии и других отраслей научных знаний) часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. Дифференциальные уравнения являются фундаментом для построения научных трудов и функционально используется в производстве, что не маловажно для современной экономики и других отраслей производства.

Теория дифференциальных уравнений (ДУ) является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.

Первая особенность – это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие – либо физические явления, исследователь прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.

Второй особенностью теории дифференциальных уравнений является ее связь с другими разделами математики, такими, как функциональный анализ, алгебра и теория вероятностей. Теория дифференциальных уравнений и особенно теория уравнений с частными производными широко используют основные понятия, идеи и методы этих областей математики и, более того, влияют на их проблематику и характер исследований. Некоторые большие и важные разделы математики были вызваны к жизни задачами теории дифференциальных уравнений.

Таким образом, теория дифференциальных уравнений в настоящее время представляет собой исключительно богатый содержанием, быстро развивающийся раздел математики, тесно связанный с другими областями математики и с ее приложениями. Исходя из этого, цель курсовой работы состоит в изучении практических приложений дифференциальных уравнений к решению задач математической модели.

Поставленная цель достигается путем решения следующих задач:

1. Изучение ДУ первого порядка, теоретические основы дифференциальных уравнений, ДУ с разделяющимися переменными;

2. Изучение линейных ДУ второго порядка с постоянными коэффициентами.

3. Решение задач математического моделирования, химии, динамики, сопротивления материалов, радиотехники и биологии.

Объект исследования – основные понятия теории дифференциального уравнения I и II порядка.

Предмет исследования – способы реализации решения задач с помощью математического моделирования на основе дифференциальных уравнений.

1.Анализ учебной и научной литературы; 2.Изучение способов и методов реализации математических моделей; 3.Обобщение результатов.

В соответствии с целью, задачами и логикой исследования работа состоит из введения, двух глав, заключения, списка использованной литературы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА

Дифференциальные уравнения первого порядка

Общие понятия и определения

Обыкновенным дифференциальным уравнением называется соотношение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы).

Порядком дифференциального уравнения называется наивысший порядок входящей в него производной (или дифференциала).

Дифференциальным уравнением первого порядка называется соотношение вида

где x – независимая переменная; y = y ( x ) – искомая функция; y ´( x ) = – её производная.

Если уравнение (1.1) можно записать в виде

то говорят, что оно разрешимо относительно производной.

Часто встречается дифференциальная форма записи уравнения первого порядка

которая удобна тем, что в качестве искомой функции может быть как x = x ( y ) , так и y = y ( x ).

Решением ( интегралом ) дифференциального уравнения первого порядка называется любая функция y = y ( x ), превращающая это уравнение в тождество.

График функции y = y ( x ) называется интегральной кривой.

Процесс решения дифференциального уравнения называется его интегрированием.

На самом деле в процессе интегрирования определится целый класс решений:

где C – произвольная постоянная.

Класс (1.3) называется общим решением дифференциального уравнения;

В некоторых случаях общее решение дифференциального уравнения определяется в неявном виде: Ф ( x, y, C ) = 0.

Геометрически общее решение представляет собой семейство интегральных кривых на плоскости xOy .

При каждом конкретном значении С = получают частное решение

Задача о нахождении решения дифференциального уравнения (1.2), удовлетворяющего начальному условию y () = , называется задачей Коши.

Геометрически, такая задача предполагает поиск интегральной кривой, которая проходит через заданную точку с координатами ( , ).

Решение дифференциального уравнения, которое не может быть получено из общего решения ни при одном частном значении произвольной постоянной (включая «предельные» случаи C = ±∞), называется его особым решением .

При интегрировании дифференциального уравнения надо стремиться к тому, чтобы наряду с общим решением были найдены также и особые решения.

Среди всех дифференциальных уравнений особый интерес представляют некоторые классы уравнений, для которых существуют стандартные способы аналитического решения.

1.1.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение вида:

называется уравнением с разделяющимися переменными.

Разделим переменные, учитывая, что y ´( x ) = .

При этом уравнение (1.4) преобразуется к виду = f ( x ) dx .

Интегрируя, получим общее решение: ʃ

1. Характерный признак дифференциальных уравнений с разделяющимися переменными – это наличие произведений (или частных) «блоков», зависящих только от « х » или только от « у ».

2. Если обе части уравнения делим на переменную величину, то необходимо отдельно рассмотреть также случай, когда она обращается в ноль. Так, постоянные у = , для которых g() = 0 , являются, очевидно, решениями уравнения (1.4).

3. Произвольная постоянная, возникающая при интегрировании, может быть записана в виде kC или klnC , где k – любой постоянный (ненулевой) множитель. В некоторых случаях такая запись удобна для упрощения ответа.

1.1.3. Линейные уравнения первого порядка. Уравнение Бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение вида

где p ( x ), q ( x ) – непрерывные (на данном интервале) функции.

Характерный признак таких уравнений – функция y и её производная содержатся в уравнении в первой степени.

Уравнение Бернулли имеет вид

Существует несколько методов решения уравнений данных видов: метод вариации произвольных постоянных, метод интегрирующего множителя, метод Бернулли.

Рассмотрим метод Бернулли . При этом решение каждого из уравнений (1.5), (1.6) будем искать в виде

По правилу дифференцирования произведения получим = v + u

(аргумент « x » в дальнейшем опускаем).

В этом случае линейное уравнение (1.6), например, записывается следующим образом

Множитель v = v ( x ) можно выбрать как некоторое решение уравнения + pv = 0 .

Тогда исходное уравнение оказывается эквивалентным уравнению с разделяющимися переменными v = q , общее решение которого есть некоторая u = u ( x , C ).

Окончательно общий интеграл линейного дифференциального уравнения примет вид

Таким образом, в процессе решения приходится дважды решать уравнения с разделяющимися переменными.

По той же схеме решается и уравнение Бернулли.

1.2. Линейные дифференциальные уравнения второго порядка

1.2.1. Основные понятия, структура общего решения

Линейным дифференциальным уравнением ( ЛДУ) второго порядка называется уравнение вида

где функции p ( x ), q ( x ), f ( x ) непрерывны на некотором интервале ( a ; b ).

Если f ( x ) ≡ 0, то уравнение (2.1) называется линейным однородным дифференциальным уравнением ( ЛОДУ ):

а в противном случае – линейным неоднородным (ЛНДУ).

Общее решение линейного однородного дифференциального уравнения имеет вид

где ( x ), ( x ) – линейно независимые решения этого уравнения (фундаментальная система решений), , – произвольные постоянные.

При этом функции ( x ) и ( x ) называются линейно независимыми в промежутке ( a ; b ), если их отношение (в этом промежутке) не является постоянной величиной. В противном случае функции называются линейно зависимыми.

Для того, чтобы частные решения уравнения (2.2) ( x ) и ( x ) были линейно независимы в промежутке ( a ; b ), необходимо и достаточно, чтобы их определитель Вронского

был отличен от нуля хотя бы в одной точке ( a ; b ).

Общее решение н y линейного неоднородного дифференциального уравнения представляет собой сумму

где – общее решение соответствующего однородного уравнения (2.2);

– некоторое частное решение неоднородного уравнения (2.1).

Остановимся подробнее на линейных уравнениях с постоянными коэффициентами, для которых существуют стандартные алгоритмы решения.

1.2.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Если в уравнении (2.2) все коэффициенты постоянны, то оно называется линейным однородным уравнением с постоянными коэффициентами

где p , q – действительные числа.

Решение этого уравнения будем искать в виде y = . Значения параметра λ определяются как решения квадратного уравнения

которое называется характеристическим уравнением.

Чтобы получить общее решение уравнения (2.5), следует воспользоваться следующим алгоритмом :

– найти корни соответствующего характеристического уравнения

– записать фундаментальную систему решений (ФСР);

– использовать формулу (2.3) для записи .

При нахождении корней характеристического уравнения (2.6) и построении ФСР возникают следующие случаи, приведённые в табл.1.

Таким образом, решение линейного однородного дифференциального уравнения с постоянными коэффициентами сводится к вышеуказанной простой последовательности действий.

Таблица. 1. – нахождении корней характеристического уравнения

1.2.3. Системы дифференциальных уравнений

В нашей курсовой работе ограничимся рассмотрением систем двух дифференциальных уравнений. С подобными системами приходится встречаться часто в теоретической механике, сопротивлении материалов и в других приложениях математики.

Система дифференциальных уравнений первого порядка вида

где t – независимая переменная; x ( t ), y ( t ) – неизвестные функции, называется нормальной .

Пара функций x = x ( t ), y = y ( t ) является решением системы (2.7), если каждое из уравнений системы они обращают в тождество.

Класс функций вида

называется общим решением системы (2.7), если при всех значениях произвольных постоянных , , соответствующая пара функций < x , y > является решением системы.

Для системы дифференциальных уравнений (2.7) можно сформулировать задачу Коши : найти решение

удовлетворяющее начальным условиям

С точки зрения механики, решить систему – значит восстановить закон движения точки по известному вектору скорости

Иногда нормальную систему дифференциальных уравнений удаётся свести к одному уравнению второго порядка, содержащему одну неизвестную функцию. Это может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одной ( метод исключения ).

Если правые части уравнений системы (2.7) являются линейными функциями, то система называется линейной.

Ограничимся рассмотрением линейной однородной системы с постоянными коэффициентами

где a , b , p , q – некоторые числа.

Тогда система (2.13) примет вид

Пусть для определённости p ≠ 0 .

Выразим х из второго уравнения системы (2.14):

Дифференцируем второе уравнение системы (2.14) по переменной t :

Затем подставляем в него из первого уравнения системы:

В полученное равенство вместо x подставим выражение ( 2.10 ):

Соотношение (2.16) – это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, его характеристическое уравнение можно записать с помощью определителя

В соответствии с корнями , найдём фундаментальную систему решений и , а затем и общее решение уравнения (2.11):

Затем из равенства (2.15) находим функцию x ( t , , ). В результате будет получено общее решение системы (2.14).

2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ.

В различных областях человеческой деятельности возникает большое число задач, которые сводятся к решению дифференциальных уравнений. Характер этих задач и методику их решения можно схематически описать примерно так. Происходит некоторый процесс, например физический, химический, биологический. Нас интересует определенная функциональная характеристика этого процесса, например закон изменения со временем температуры или давления, массы, положения в пространстве.

Если имеется достаточно полная информация о течении этого процесса, то можно попытаться построить его математическую модель. Во многих случаях такой моделью служит дифференциальное уравнение, одним из решений которого является искомая функциональная характеристика процесса.

Дифференциальное уравнение моделирует процесс в том смысле, что оно описывает эволюцию процесса, характер происходящих с материальной системой изменений, возможные варианты этих изменений в зависимости от первоначального состояния системы.

2.1. Математическое моделирование некоторых задач химии.

Задача 1. В результате химической реакции между веществами А и B образуется вещество C . Установить зависимость количества вещества C от времени, если в момент вступления в реакцию количества веществ A и B были равны соответственно a и b . Скорость реакции пропорциональна произведению реагирующих масс.

Решение. Пусть x = x ( t ) – количество вещества C через время t после начала реакции;

– скорость образования вещества (скорость реакции). По условию

= k ( a – x ) ( b – x ), где k > 0 – коэффициент пропорциональности. Разделяем переменные и решаем уравнение:

Из начального условия x (0) = 0 находим , тогда

Выразим из этого равенства x , получим:

Если количества веществ A и B равны, т.е. a = b , то уравнение реакции примет вид:

С учётом начального условия процесс реакции описывается зависимостью x ( t ) =

2.2. Математическое моделирование некоторых задач сопротивления материалов

Задача 2. В сопротивлении материалов доказывается, что дифференциальное уравнение изогнутой оси простой балки постоянного сечения, несущей сплошную равномерно распределённую нагрузку интенсивностью q , имеет вид

где ω – прогиб балки в сечении с абсциссой x ; EI – постоянная величина, так называемая «жёсткость на изгиб сечения балки»; l – длина балки.

Найти решение этого уравнения, удовлетворяющее краевым (граничным) условиям ω(0) = 0, ω( l ) = 0, т.е. в том случае, когда на концах балки прогиб равен нулю.

Решение. Уравнение (3.7) – это уравнение второго порядка, которое допускает понижение порядка. Решим его, последовательно (дважды) интегрируя:

Первое краевое условие даёт значение = 0 , второе – значение

Искомое решение краевой задачи есть

2.3. Математическое моделирование некоторых задач динамики

Задача 3. В последовательном контуре наблюдаются свободные колебания, если отсутствует внешний источник, и конденсатор был заряжен к моменту замыкания ключа S .

После замыкания ключа S в момент времени t = 0 конденсатор разряжается через цепь с коэффициентом самоиндукции L и сопротивлением R (рис. 1). Определить напряжение на обкладках конденсатора, если в начальный момент времени

Решение. На основании законов Кирхгофа имеем:

Таким образом, получаем дифференциальное уравнение, описывающее процессы в цепи:

где α = – коэффициент затухания; – частота собственных колебаний.

Уравнение (3.2) – это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Поскольку в задании даны ещё начальные условия, то мы имеем задачу Коши.

Характеристическое уравнение, соответствующее (3.2):

Рассмотрим три случая для корней характеристического уравнения:

С учётом начальных условий решение задачи

Коши в этом случае будет иметь вид:

Если > 0 , то напряжение стремится к нулю. В контуре наблюдаются периодические, с периодом , затухающие по экспоненциальному закону колебания. Если R = 0 (т.е. отсутствует активная составляющая цепи), то напряжение на обкладках конденсатора изменяется периодически по гармоническому закону с периодом :

(гармонический колебательный процесс).

б) D = 4Решение задачи Коши в данном случае имеет

Напряжение ( t ) стремится к нулю при t → +∞ и изменяется без колебаний (затухающий апериодический процесс).

Напряжение ( t ) стремится к нулю при t → +∞ , колебаний нет, и конденсатор апериодически разряжается.

2.4. Математическое моделирование некоторых задач радиотехники

Задача 4. Найти решение системы дифференциальных уравнений

удовлетворяющее начальным условиям x (0) = y (0) = 0 , x ´(0) = μ , y ´(0) = ƞ (здесь k и g – постоянные величины).

Решение. Предложенная система описывает движение снаряда с учётом сопротивления среды. Каждое уравнение системы содержит только одну неизвестную функцию. Из первого уравнения системы имеем

Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Его общее решение есть x ( t ) = + .

Для вычисления констант , используем начальные условия, в результате чего получим:

Итак, частное решение первого уравнения системы принимает вид:

Второе уравнение системы – это линейное неоднородное уравнение второго порядка с правой частью специального вида:

Общее решение второго уравнения системы:

Используя начальные условия, найдём значения , :

Тогда решение второго уравнения системы:

Окончательно получим параметрические уравнения траектории снаряда:

Если исключить параметр t из этих уравнений, то окажется, что:

Отсюда при y = 0 можно найти горизонтальную дальность стрельбы:

2.5. Математическое моделирование некоторых задач биологии

Живой организм представляет собой слишком сложную систему, чтобы его можно было рассматривать сразу во всех подробностях; поэтому исследователь всегда выбирает упрощённую точку зрения, подходящую для решения конкретно поставленной задачи. Это сознательное упрощение реальных биосистем и лежит в основе метода моделирования.

Обычно, модели, используемые в биологии, делят на три категории:

1.Биологические предметные модели, на которых изучаются общие закономерности, патологические процессы, действие различных препаратов и т. д. К этому классу моделей относят, например, лабораторных животных, изолированные органы. Культуры клеток, суспензии органелл и пр.

2.Физические ( аналоговые ) модели, т. е. физические модели, обладающие аналогичным с моделируемым объектом поведением. Например, деформации, возникающие в кости при различных нагрузках, могут быть изучены на специально подготовленном макете кости. Движение крови по крупным сосудам моделируется цепочкой резисторов, конденсаторов и индуктивных катушек.

3.Математические модели представляют собой системы математических выражений – формул, функций, уравнений и т. д., описывающих те или иные свойства изучаемого объекта, явления, процесса. При создании математической модели используют физические закономерности, выявленные при экспериментальном изучении объекта моделирования. Так, например, математическая модель кровообращения основано на законах гидродинамики.

Математическое моделирование, как метод исследования обладает рядом несомненных достоинств.

Во – первых, сам метод изложения количественных закономерностей математическим языком точен и экономичен.

Во–вторых, проверка гипотез, сформулированных на основе опытных данных, может быть осуществлена путём испытания математической модели, созданной на основе этой гипотезы. Наконец, математическая модель позволяет судить о поведении таких систем и в таких условиях, которые трудно создать в эксперименте или в клинике, изучать работу исследуемой системы целиком или работу её любой отдельной части.

Задача 5. Определить во сколько раз увеличится количество бактерий за 9 часов, если в течение 3 часов их количество изменилось от 100 да 200.

Решение. Опытным путём установлено, что скорость размножения бактерий, если для них имеется достаточный запас пищи и созданы другие необходимые внешние условия (например, отсутствие подавления бактерий другими видами), пропорциональна их количеству.

Пусть х – количество бактерий, имеющееся в данный момент, тогда скорость изменения их количества:

Так как скорость размножения бактерий пропорциональна их количеству, то существует такая k, что:

Разделяем в дифференциальном уравнении переменные:

что после потенцирования даёт:

Для нахождения С используем начальное условие: при t = 0 х = 100 . Имеем: Се˚ = 100, С = 100, и, значит , х = 100 е kt .

Коэффициент е k находим из условия: при t = 3 х = 200. Имеем:

Ответ: Количество бактерий за 9 часов увеличится в 8 раз.

Заметим, что закон, при котором скорость увеличения вещества пропорциональна наличному количеству вещества это, так называемый, закон «естественного роста».

Эта математическая модель процесса изменения количества микроорганизмов в колонии в зависимости от времени получена при очень больших предположениях (при неограниченных ресурсах питания и пространства для обитания и отсутствии межвидовой борьбы). В природе же, ни в одной из реально существующих колоний такой рост наблюдаться не может.

Ответ на вопрос, насколько закон «естественного роста» отвечает реальному процессу, даёт опытная проверка. Очевидно, что на каком-то подмножестве данные будут хорошо согласованы с моделью, а саму модель можно использовать для прогноза.

В 1845 году Ферхюлст – Перл получил уравнение, учитывающее внутривидовую борьбу микроорганизмов. В результате конкурентной борьбы внутри вида за пищу и место распространения, а так же за счёт болезней скорость роста снижается. В общем виде уменьшение прироста является некоторой новой функцией от х и Δх, которую обозначим через b ( х, Δх ) . Уменьшение количества особей в результате конкуренции тем больше, чем больше число встреч между особями, т. е. пропорционально произведению х-х т. е. х 2 . Таким образом,

Здесь ε – специфическая (врождённая) скорость размножения популяции, δ – коэффициент внутривидовой конкуренции. Разделим обе части последнего уравнения на Δt и переходя к пределу, получим

Это и есть уравнение Ферхюлста – Перла. Решением этого уравнения после математических преобразований и обозначения ε/ δ = h при t ₀ = 0 и х(0) = х ₀ является:

ЗАКЛЮЧЕНИЕ

Изучение большого круга задач сопротивления материалов, динамики, биологии и других отраслей научных знаний показывает, что решение многих из них сводится к математическому моделированию процессов в виде формулы, т.е. в виде функциональной зависимости.

Так, например, некоторые процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью уравнений, в которых кроме независимых переменных и неизвестных функций этих переменных, содержатся производные неизвестных функций (или их дифференциалы).

Такие уравнения называются дифференциальными.

Вот почему возможности применения дифференциальных уравнений для решения задач по дисциплинам естественно – научного цикла довольно широки.

В представленной работе:

– описаны теоретические основы дифференциальных уравнений;

– рассмотрены некоторые приёмы решения задач с помощью дифференциальных уравнений по химии, радиотехники, биологии, сопротивления материалов и динамики.

В ходе работы, возникла необходимость более полного, чем предполагалось, изучения основ моделирования реальных объектов.

Практическая ценность метода математического моделирования заключается в следующем:

– правильно составленная и всесторонне использованная математическая модель позволяет оптимизировать изучение реальной системы по времени;

– математическая модель позволяет облегчить прогнозирование хода и результатов экспериментов, проводимых в реальных системах.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Агафонов, С.А. Дифференциальные уравнения / С.А. Агафонов, А.Д. Герман, Т.В. Муратова. – МГТУ им. Н.Э. Баумана, 2004. (Сер. Математика в техническом университете; Вып. VII).

2. Берман, Г.Н. Сборник задач по курсу математического анализа: учебное пособие / Г.Н. Берман. – 22-е изд., перераб. – Спб. : Профессия, 2005.

3. Данко, П.Е. Высшая математика в упражнениях и задачах : учебное пособие для вузов. В 2 ч. Ч. 2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»; ООО Издательство «Мир и образование», 2006.

4. Каплан, И.А. Практикум по высшей математике : учебное пособие. В 2 т. Т. 2 / И.А. Каплан, В.И. Пустынников ; под общей ред. проф. В.И. Пустынникова. – 6-е изд., испр. и доп. – М. : Эксмо, 2008. (Образовательный стандарт XXI).

5. Мышкис, А.Д. Прикладная математика для инженеров. Специальные курсы / А.Д. Мышкис. – 3-е изд., доп. – М. : ФИЗМАТЛИТ, 2007.

6. Нахман, А.Д. Сборник задач по дифференциальным уравнениям и их приложениям : учебное пособие / А.Д. Нахман, С.В. Плотникова. – Тамбов : Издательство Тамб. гос. техн. ун-та, 2005.

7. Нахман, А.Д. Дифференциальные уравнения : методическое пособие / А.Д. Нахман. – Тамбов : ТОИПКРО, 2007.

8. Сборник задач по высшей математике. 2 курс / К.Н. Лунгу и др.; под ред. С.Н. Федина. – 5-е изд. – М. : Айрис-пресс, 2007.

9. Самойленко, А.М. Дифференциальные уравнения: примеры и задачи : учебное пособие / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. – 2-е изд., перераб. – М. : Высшая школа, 1989.

Дифференциальные уравнения и математическое моделирование

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

научный руководитель канд. физ.-мат. наук, проф.

Лесосибирский педагогический институт – филиал ФГАОУ «Сибирский федеральный университет»

Для изучения объектов или процессов, протекающих в окружающем нас мире, широко используются методы математического моделирования. Математические модели являются мощным средством познания окружающего мира. При этом следует заметить, что построенная математическая модель не может отразить все многообразные и сложные черты изучаемого явления. При моделировании что-то является главным, а что-то – второстепенным, чем можно пренебречь.

Изучение большого круга задач естествознания, техники и механики, биологии, медицины и других отраслей научных знаний показывает, что решение многих из них сводится к математическому моделированию процессов в виде формулы, т. е. в виде функциональной зависимости.

Так, например, некоторые процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью уравнений, в которых кроме независимых переменных и неизвестных функций этих переменных, содержатся производные неизвестных функций (или их дифференциалы). Такие уравнения называются дифференциальными.

Вот почему возможности применения дифференциальных уравнений для решения задач по дисциплинам естественно – научного цикла довольно широки. Обыкновенные дифференциальные уравнения моделируют явления и процессы, которые описываются одной функцией или вектор-функцией одного переменного.

В математическое исследование любой задачи реального мира можно выделить три основных этапа:

1. построение математической модели явления;

2. изучение этой математической модели и получение решения соответствующей математической задачи;

3. приложение полученных результатов к практическому вопросу, из разрешения которого возникла данная математическая модель, и отыскание других вопросов, к которым она применима.

В таблице представлены основные области наук, в которых какое-либо явление или процесс можно записать в виде дифференциального уравнения.

Характеристика составления математической модели

Пример математической модели

1. Установить величины, изменяющиеся в данном явлении, и выявить физические законы, связывающие их.

2. Выбрать независимую переменную и функцию этой искомой переменной.

3. Исходя из условий задачи, определить начальные или краевые условия.

4. Выразить все фигурирующие в условии задачи величины через независимую переменную, искомую функцию и производные этой функции.

5. Исходя из условий задачи и физического закона, которому подчиняется данное явление, составить дифференциальное уравнение.

6. Найти общее решение или общий интеграл дифференциального уравнения.

7. По начальным или краевым условиям найти частное решение.

8. Исследовать полученное решение.

А) Первый закон Ньютона:

Б) Уравнение показательного роста и показательного убывания:

где – некоторая константа.

В) Уравнение гармонического колебания:

где – положительная постоянная.

где – радиус Земли, – расстояние между центрами метеороида и Земли, – ускорение свободного падения.

1. Сделать чертёж и ввести обозначения;

2. Отделить условия. Имеющие место в произвольной точке искомой линии, от условий, выполняющихся лишь в отдельных точках;

3. Выразить все упомянутые в задаче величины через координаты произвольной точки и через значение производной в этой точке, учитывая геометрический смысл производной;

4. По условию задачи составить дифференциальное уравнение;

5. Найти общее решение этого уравнения и получить из него с помощью начальных условий уравнение искомой линии.

Формула зеркала, собирающего все параллельные лучи в одну точку:

При создании математической модели используют физические закономерности, выявленные при экспериментальном изучении объекта моделирования. Так, например, математическая модель кровообращения основано на законах гидродинамики.

Модель хищник – жертва:

где – положительные константы, – число хищников, – число жертв.

Сущность химических реакций сводится к разрыву связей в исходных веществах и возникновению новых связей в продуктах реакции. При этом общее число атомов каждого элемента до и после реакции остаётся постоянным.

Закон действующих масс:

где – концентрации веществ

– коэффициент пропорциональности.

Базовая математическая модель в области финансов формулируется в терминах стохастических процессов, приводящих, таким образом, к стохастическим дифференциальным уравнениям. Время и недостоверность являются главными элементами моделирования финансового поведения экономических агентов.

Модель фондового (биржевого) ценообразования:

где и – постоянные коэффициенты, связанные с характеристиками модели.

Компартментальное моделирование распространено в медицине и биологии. Согласно определению американского фармаколога и биохимика Шеппарда компартмент — это некоторое количество вещества, выделяемое в биологической системе и обладающее свойством единства, поэтому в процессах транспорта и химических преобразований его можно рассматривать как целое. Например, в качестве особых компартментов рассматривают весь кислород в легких, всю углекислоту в венозной крови, количество введенного препарата в межклеточной жидкости, запас гликогена в печени и т. п. Модели, в которых исследуемая система представляется в виде совокупности компартментов, потоков вещества между ними, а также источников и стоков всех веществ, называются компартментальными.

Модель роста опухоли:

где – концентрация опухолевых клеток, – внеклеточная матрица (например, IV тип коллагена).

В заключение отметим, что математическая модель является основой математически оформленной теории того или иного явления, а аппарат дифференциальных уравнений нашел большое применение в математическом моделировании.
Результативность математического моделирования подтверждена всей человеческой практикой, это сильное средство научного исследования, которое используют в каждой конкретной области науки.

Классическая механика: о диффурах «на пальцах»

Введение

В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…

Физический смысл

В своей статье про Фильтр Калмана я описал что такое уравнения вида «вход-выход», передаточная функция и операторная форма записи дифференциальных уравнений (см. раздел «Основные понятия» в [2]). Примером части математической модели динамического объекта в операторной форме записи может служить следующее уравнение:
(1)
Это распространенная упрощенная модель динамических систем. Опережая напишу, что модель тела в движке «Farseer» использует урезанный аналог представленной выше модели (динамического звена второго порядка). Ниже представлено описание принятых в ней обозначений.

• а0, а1, а2 — коэффициенты инерции, демпфирования и жесткости, соответственно.
• b0, b1 — коэффициенты входного воздействия.
• s — оператор Лапласса (d/dt).
• α(s), β(s) — выходная и входная переменные, как функции оператора Лапласса.

Представленное уравнение описывает динамическую систему типа «один вход — один выход» (SISO). Ее можно использовать для описания динамики объекта по одной из его степеней свободы. Как Вам, возможно, известно, у свободного тела есть шесть степеней свободы — три поступательные (линейное движение вдоль трех осей системы координат (СК) ) и три вращательные (повороты вокруг осей СК). Таким образом, полная модель физического тела будет описываться шестью такими уравнениями (или четырьмя для 2D случая). Вы сразу можете сказать, что уже это свидетельствует о слишком высокой сложности такого подхода. Но на самом деле в Farseer, к примеру, класс тела (Body) содержит и линейные координаты тела (по сути это пара α(s) по OX и OY), и линейные скорости (пара s*α(s) по OX и OY) и параметры ориентации и угловой скорости. Эти параметры обсчитываются раздельно для каждой из осей, т.е. количество уравнений такое же — два уравнения по оси OX (линейное и угловое движение) и два для оси OY. Разница лишь в форме уравнений.
Алгоритм в движке Farseer — приближенный и упрощенный, но позволяет работать с варьируемыми квантами времени. В функцию обсчета параметров движения (Island.Solve(ref TimeStep step, ref Vector2 gravity)) передается время, прошедшее после последнего обсчета параметров. Это позволяет при недостаточной производительности компьютера держать скорость течения игрового времени примерно постоянным в ущерб плавности и реалистичности движения игровых объектов.
При построении дискретной модели на основе диференциальных уравнений мы четко завязываемся на фиксированный квант времени. Уравнения интегрируются для изначально заданной частоты дискретезации, и если с момента последнего обсчета по какой-то причине прошло времени больше, чем заданный квант (в англоязычной литературе его называют «time sample»), то мы либо должны произвести обсчет несколько раз, либо получим замедление движения объекта. Последнее я как раз и наблюдал в игре «Command Cortex» на слабой машине. Движения акторов были плавными но медленными (акторы, управляемые человеком, получают преимущество). Таким образом, нельзя говорить об исключительном преимуществе одного из этих подходов.
Теперь о том, за что отвечают коэффициенты представленного выше уравнения. Это уравнение описывает движение физического тела относительно положения равновесия при α(s) = 0. Это еще одна из причин кажущегося неудобства применения такой модели в игровой механике. При отсутствии приложенных внешних сил данная модель рано или поздно возвратит (при условии устойчивости модели) тело в положение равновесия. Представьте игровой мир, наполненный шариками, которые все время стремятся в начало координат (например, в левый верхний угол экрана). К такому поведению приводит наличие коэффициента жесткости (см. а2 выше). Представьте, что тело соединено с началом координат пружиной. Пока на тело действуют силы, пружина растянута, но стоит убрать внешнее воздействие и тело устремится к нулю. Тела в движке Farseer таким поведением не обладают. Если мы зададим коэффициент a2 равным нулю, то и в данном случае тела не будут стремиться к началу координат (см. выше я писал, что модели в Farseer по сути урезанные варианты этой модели). Ну и зачем этот коэффициент тогда нужен, спросите Вы. Если раскрыть скобки в левой части уравнения (1) и вместо слагаемого
a2*α(s)
напишем
a2*(α(s) — α0)
то через α0 мы получим возможность задать положение, к которому игровой объект будет стремиться. Величина коэффициента а2 отвечает за то, насколько быстро тело переместится в заданное положение равновесия (чем больше значение, тем выше жесткость пружины). Как такое реализовывается в Farseer я пока не выяснил, но думаю придется создать дополнительный источник воздействия.
Теперь коэффициент a1. Это коэффициент демпфирования. Чем больше значение этого коэффициента, тем быстрее гасится скорость (линейная или угловая). Аналогия из жизни — вязкие жидкости, такие как масло, мед, эпоксидная смола. Эти жидкости очень вязкие (имеют большое значение коэффициента демпфирования). Чем выше скорость движения тела в них, тем выше сопротивление этому движения. Если медленно двигать в них ложку, например, то преодолеть сопротивление большого труда не составит, а вот если ударить с размаху, то удар будет жестким.
Величина коэффициента а0 характеризует инерцию объекта. При описании линейного движения в качестве коэффициента а0 используется масса. Чем выше его значение, тем медленнее тело набирает скорость при приложении к нему внешних сил.
Теперь о коэффициентах в правой части уравнения (1). Тут нужно заметить, что данная модель расширенная на случай, когда входное воздействие определяется не только самим значением внешней силы, но и ее изменением. Для описания динамики игровых объектов это, возможно, будет излишним. Однако в промышленных системах управление встречаются и такие модели. Каков же их физический смысл? Коэффициент b1 это по сути коэффициент передачи внешней силы вовнутрь объекта. Обычно он равен еденице, т.е. сила передается как есть.
Коэффициент b0 интересен. Он играет роль форсирующего коэффициента. Представьте очень инерционный объект, к которому прикладывают силу, плавно нарастающую со временем. Если скорость нарастания и конечная величина силы будут малы, то объект очень медленно набирать скорость. Но если силу сделать большой, то после достижения внешней силой заданного значения объект не остановится в каком-то положении, а будет колебаться под действием инерции. Форсирование — это воздействие, пропорциональное скорости нарастания внешней силы. Если мы выберем его большим, то даже при малой скорости нарастания внешней силы наш объект будет достаточно быстро набирать скорость, а когда внешняя сила достигнет заданного значения, форсирование отключится. Вот такой вот хитрый этот «b0».

Динамика в картинках

Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])

Transfer function «w» from input «u1» to output…

y1: (s + 1)/(s^2 + s + 1)

Continuous-time model.
=========================================


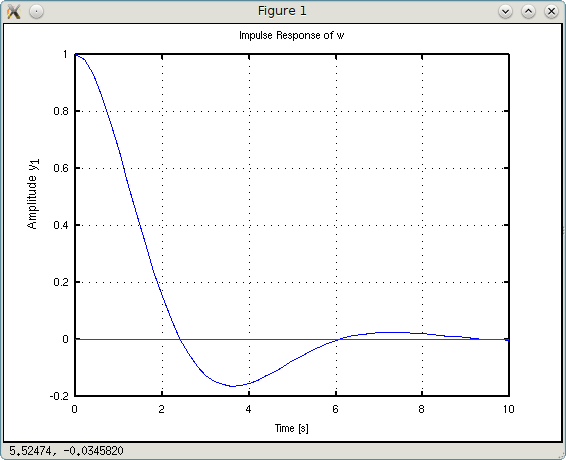
Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).

Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)

>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице.


Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.

Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)

>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1)


Сразу вывод: больше вязкость — быстрее затухают колебания.

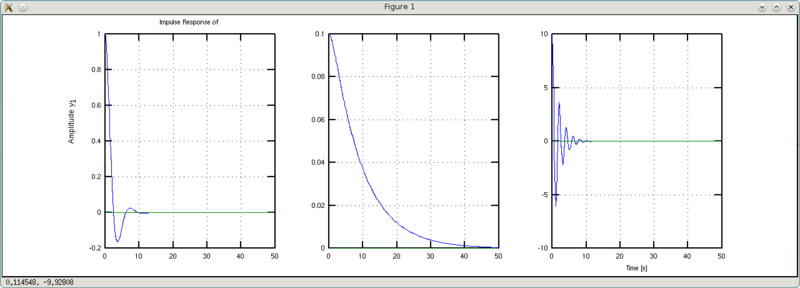
Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)

>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1)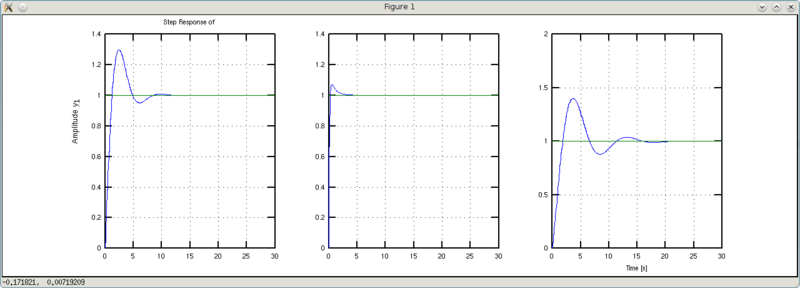


Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.

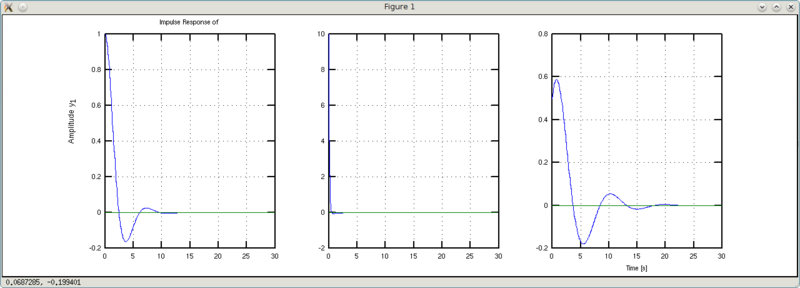
Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)

>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1)


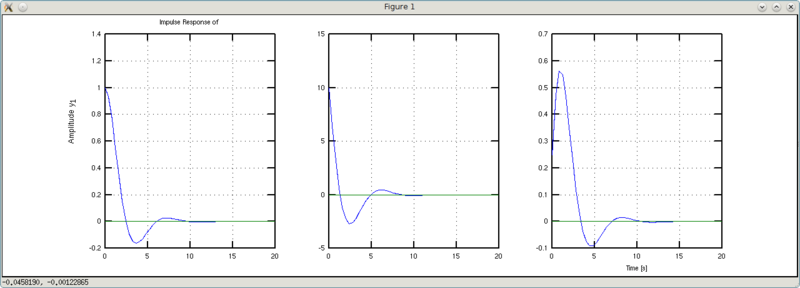
Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).

И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)

>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1)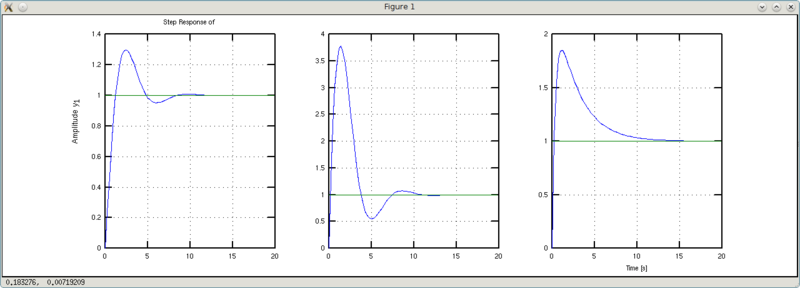


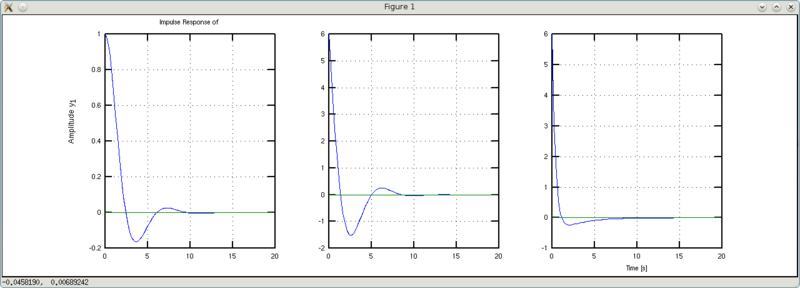
Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.

На правах PS

В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.