методами Эйлера и Рунге-Кутта в системе MathCAD
Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка


Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
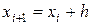
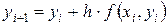
Рассмотрим реализацию метода в MathCADна примере уравнения:
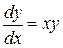
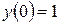
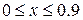
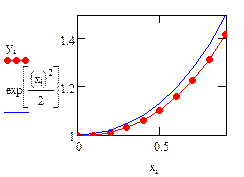
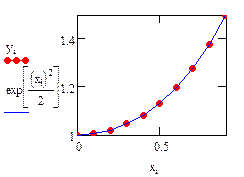
Аналитическое решение известно и имеет вид:

Краткие сведения о составлении программ в MathCAD
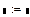
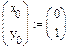
Графиквставляется командой Insert→ Graph→ X-YPlotили клавишей «@».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка 
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
Программа для простого метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
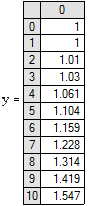
| Результаты решения: |
 |
 |
 |
 |
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
| Итерационные уравнения |
 |
| Результаты решения: |
 |
 |
 |
 |
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя: |
 |
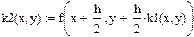 |
 |
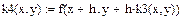 |
 |
| Усредненная функция |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
 |
 |
Решение дифференциальных уравнений 2-го порядкаметодом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции 


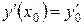
Преобразуем задачу к системе из двух уравнений:


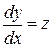

Тогда получим следующее обобщение итерационной схемы:



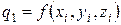
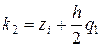




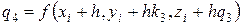
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:

где t– время, и искомой является зависимость 
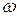
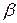
Если 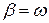

где Aи 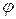
Когда 

В этом случае колебательный процесс слагается из собственных колебаний с частотой 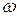
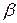
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:

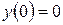


Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
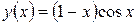
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
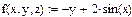 |
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z) |
| Задание коэффициентов как функций пользователя: |
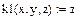 |
 |
 |
 |
 |
 |
 |
 |
| Усредненные функции: |
 |
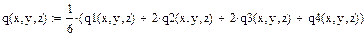 |
 |
| Задание цикла |
 |
| Задание начальных условий |
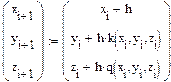 |
| Итерационные уравнения |
 |
| Результаты решения: |
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:

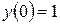
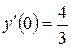
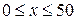
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
Дифференциальные уравнения в MathCad
Дифференциальные уравнения достаточно часто используются для того, чтобы описать значение часто меняющихся процессов. Сначала обратим внимание на самое стандартное уравнение данного типа.
Решение данного уравнения будет представлено следующим образом.
И это решение отличается максимально точным. Кроме того, оно отличается отменной результативностью. Жаль, что многие дифференциальные уравнения нереально решить при помощи аналитики. Мы часто вынуждены прибегать к численным методикам.
Метод Эйлера
Этот метод отличается максимальным удобством и простотой для решения уравнений дифференциального типа. Его достаточно легко понять и реализовать в сфере программирования.
Постепенно проследим изменения
Сравниваем результативность и правильный ответ
Необходимо учитывать, что методика Эйлера в некоторой степени отличается от точного решения задачи. И чем выше аргумент, тем внушительнее оказывается полученная разница. Чтобы свести к минимуму ошибку, нужно увеличить количество шагов.
Блок решения ОДУ
Mathcad вмещает в себя все самые важные опции для решения уравнения дифференциального типа. В данном уроке мы обратим внимание на самую важную функцию такого типа. Она характеризуется максимальной точностью и простотой использования. Методика сочетает пользование блоком решения и опцией odesolve(). Перед решением устанавливаем такие параметры:
Каждое вхождение переменной с в блок решения представляется как функция независимой переменной.
Данный метод во многом похож на принципы аналитического решения. Точно такой же результат удается получить после записи производной через штрих (Ctrl+’)
Сердце и артерии
Функционирование сердца и артерий во многом похожи на работу насоса. Они оба могут расшириться и сжаться, а клапаны перегоняют жидкость исключительно в одном направлении.
Пульсирование потока можно снизить, расширяя и сжимая стенки артерии.
Перепады давления возле легких достаточно низкие. Давайте установим, что повышенное давлении в точках А и В равняется нулю. Центральный элемент – это артерия, которая может изменяться в объемах.
Допустим, что объемы сердца могут изменяться в соответствии с особенностями синусоидального закона. Однако впырск крови происходит исключительно во время положительных полуволн.
График для восьми ударов:
Средний поток представляет собой интеграл объема, который задействован при одном ударе и поделен на его продолжительность.
Расширение артерий прямо зависит от общей эластичности стенок и особенностей их строений. Однако мы в математических целях предположим, будто объем прямо зависит от превышения давления.
Чем выше эластичность стенки, тем больше оказывается значение k. Установим ему три значения.
Баланс объемов артерий:
Вышеуказанная формула приводит к таковым результатам:
Данную функцию можно решить примерно так же, как и предыдущую. Единственное различие состоит в том, что k будет перенесено в блок решения уже в качестве параметра.
Теперь конвертируем решения.
Максимальные показания давления прямо зависят от уровня эластичности давления. Чем она выше, тем ниже оказывается само давление.
Так, вышеуказанный пример потребовал использование всего одного уравнения первого порядкового уровня. Однако программа Маткад не ограничивается данным функционалом.
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
Дифференциальные уравнения методом эйлера маткад
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
 |  |
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
 |
 |
 |




































