Energy
education
сайт для тех, кто хочет изучать энергетику
Метрология и автоматизация
Система управления
Система управления — строго определённый набор средств сбора сведений о подконтрольном объекте и средств воздействия на его поведение, предназначенный для достижения определённых целей. Объектом системы управления могут быть как технические объекты, так и люди.
3. Модели линейных объектов
Дифференциальные уравнения
Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка.
Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта – напряжение якоря $u(t)$ (в вольтах), выход – угол поворота вала $θ(t)$ (в радианах).
Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения $ω(t)$ (в радианах в секунду) остается постоянной, при этом угол $θ(t)$ равномерно увеличивается.
Чем больше напряжение, тем быстрее вращается вал. Если подключить нагрузку, например, заставить двигатель вращать турбину, скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.
Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения $ω(t)$ вычисляется как производная от угла поворота вала $θ(t)$, то есть
Соответственно, угол $θ(t)$ – это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде
где $M(t)$ – вращающий момент (измеряется в H·м), $M_н (t)$ – момент нагрузки (возмущение, также в H·м). Буквой $J$ обозначен суммарный момент инерции якоря и нагрузки (в кг·м 2 ). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).
Перейдем к электротехнике. В нашем случае момент $M(t)$ – это электромагнитный момент двигателя, который вычисляется по формуле
где $C_м$ – коэффициент, $Ф$ – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); $i(t)$ – ток якоря (в амперах), который может быть найден из уравнения
где $e(t)$ – электродвижущая сила (ЭДС) якоря (в вольтах) и $R$ – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения:
где $C_ω$ – коэффициент. Вводя новые постоянные $k_1=C_м·Ф$ и $k_2=C_ω·Ф$, можно записать модель двигателя в виде системы уравнений
Модель описывает связи реальных сигналов в системе, ее внутреннее устройство.
Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Переходя к переменной $θ(t)$, получаем:
или, перенося все члены, зависящие от $θ(t)$, в левую часть равенства
Это дифференциальное уравнение второго порядка, связывающее вход $u(t)$ и нагрузку $M_н (t)$ с выходом $θ(t)$. В сравнении с системой, все внутренние сигналы исходной модели $e(t)$ и $i(t)$ были исключены из уравнений. Поэтому последнее уравнение называется уравнением «вход-выход».
Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.
В этом разделе на простом примере рассмотрено, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения.
Модели в пространстве состояний
Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.
Рассмотрим снова модель электродвигателя, считая, что $M_н (t)=0$ (нагрузки нет). Вспомнив, что $ω(t)=\frac<\mathrm
Эта система дифференциальных уравнений первого порядка быть записана в матричной форме:
Значения $θ(t)$ и $ω(t)$ определяют состояние двигателя в момент времени $t$. Это значит, что зная их значения в некоторый момент времени $t_0$ и входной сигнал $u(t)$ при всех $t≥t_0$ можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения $θ(t)$, $ω(t)$ и $u(t)$ (при $t 0$ дает возможность однозначно определить дальнейшее поведение этого объекта.
Первое уравнение в системе позволяет найти производную, то есть, скорость изменения вектора состояния $x(t)$ в любой момент времени. Будем считать, что при $0≤t≤∆t$, где $∆t$ – малый интервал времени, эта производная не меняется. Тогда значение вектора состояния при $t=∆t$ приближенно определяется формулой
то есть, его можно легко вычислить. Зная $x(∆t)$ и сигнал управления $u(∆t)$, находим выход системы в тот же момент
Эту методику можно применять и дальше, в конце второго интервала получаем
Таким образом, можно (приближенно) рассчитать выход системы при всех $t>0$. Конечно, точность будет тем выше, чем меньше $∆t$, однако объем вычислений при этом также увеличится.
Этот метод приближенного решения дифференциальных уравнения называется методом Эйлера.
Передаточная функция
Выходной сигнал системы можно представить как результат действия некоторого оператора на ее вход. Для линейных моделей такой оператор можно записать следующим образом.
Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход $x(t)$ и выход $y(t)$:
где $a_i (i=0,1)$ и $b_i (i=0,1,2)$ – постоянные. Введем оператор дифференцирования $p=\frac<\mathrm
Теперь запишем производные сигналов $x(t)$ и $y(t)$ по времени в операторной форме
Подставляя эти выражения, получим
$$b_2 p^2\ y(t)+b_1 p\ y(t)+b_0 y(t)=a_1 p\ x(t)+a_0 x(t).$$
Можно формально вынести за скобки $y(t)$ в левой части равенства и $x(t)$ в правой части:
$$(b_2 p^2+b_1 p+b_0 )y(t)=(a_1 p+a_0 )x(t).$$
Левая часть означает, что оператор $b_2 p^2+b_1 p+b_0$ действует на сигнал $y(t)$, а в правой части оператор $a_1 p+a_0$ действует на сигнал $x(t)$. «Разделив» (условно, конечно) обе части на оператор $b_2 p^2+b_1 p+b_0$, связь выхода и входа можно записать в виде
где запись $W(p)·x(t)$ означает не умножение, а действие сложного оператора
на сигнал $x(t)$. Иначе говоря, формула $y(t)=W(p)·x(t)$ – это не что иное, как символическая запись, которую удобно использовать.
Функция $W(p)$ называется передаточной функцией объекта. Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
Часто передаточной функцией называют функцию $W(λ)$, которая получается в результате замены оператора $p$ на некоторую независимую переменную $λ$. Эта фукнция представляет собой отношение двух полиномов (многочленов) от $λ$.
Передаточная функция $W(λ)$ называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Например, функция $\frac<1><λ+1>$ – строго правильная и одновременно правильная; $\frac<λ><λ+1>$ – правильная, но не строго правильная (иногда такие функции называют биправильными), а $\frac<λ^2+λ+1><λ+1>$ – неправильная.
Нулями передаточной функции называются корни ее числителя, а полюсами – корни знаменателя. Например, функция
имеет нуль в точке $λ=1$ и два полюса в точках $λ=-1$ и $λ=-2$.
Преобразование Лапласа
Одна из первых задач, которые были поставлены в теории управления – вычисление выхода системы при известном входе. Мы видели, что для ее решения нужно решать дифференциальные уравнения. Чтобы упростить процедуру, математики придумали преобразование, которое позволило заменить решение дифференциальных уравнений алгебраическими вычислениями, то есть, операциями с полиномами (многочленами) и рациональными функциями.
Для функции $f(t)$ вводится преобразование Лапласа, которое обозначается как $\mathscr
Функция $F(s)$ называется изображением для функции $f(t)$ (оригинала). Здесь $s$ – это комплексная переменная, которая выбирается так, чтобы интеграл сходился.
Обратное преобразование Лапласа $\mathscr
где $j=\sqrt<-1>$, а постоянная σ выбирается так, чтобы интеграл сходился.
На практике вместо интеграла чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот. Например, изображения по Лапласу для дельта-функции, единичного скачка и функции $e^<-a·t>$ равны, соответственно
Преобразование Лапласа имеет несколько замечательных свойств. Во-первых, легко доказать, что принцип суперпозиции выполняется как для прямого, так и для обратного преобразования Лапласа:
Во-вторых, изображение для производной функции $f(t)$ равно
где $F(s)$ – изображение функции $f(t)$, и $f(0)$ – ее значение при $t=0$. Поэтому при нулевых начальных условиях изображение производной равно изображению самой функции, умноженному на $s$. Аналогично для построения изображения i-ой производной нужно умножить изображение функции на $s^i$ (это также справедливо только при нулевых начальных условиях).
Кроме того, с помощью преобразование Лапласа можно сразу найти начальное и конечное значения функции-оригинала (при $t=0$ и $t→∞$), не вычисляя самого оригинала:
Рассмотрим снова уравнение
Применим к левой и правой частям преобразование Лапласа, считая, что все начальные условия нулевые. Получается уравнение в изображениях, связывающее преобразования Лапласа входа $X(s)$ и выхода $Y(s)$:
$$b_2 s^2 Y(s)+b_1 sY(s)+b_0 Y(s)=a_1 sX(s)+a_0 X(s).$$
Можно вынести за скобки $Y(s)$ в левой части и $X(s)$ в правой части:
$$(b_2 s^2+b_1 s+b_0 )Y(s)=(a_1 s+a_0 )X(s).$$
Разделив обе части этого равенства на $b_2 s^2+b_1 s+b_0$, получаем
$$Y(s)=(a_1 s+a_0)/(b_2 s^2+b_1 s+b_0 ) X(s)=W(s)·X(s).$$
$W(s)$ – это передаточная функция объекта, записанная в виде функции от комплексной переменной $s$, а не от оператора дифференцирования $p$.
Таким образом, при нулевых начальных условиях изображение выхода линейного объекта вычисляется как произведение его передаточной функции на изображение входного сигнала.
Из этого следует и другой важный вывод: передаточная функция равна отношению изображений по Лапласу выхода и входа при нулевых начальных условиях.
Рассмотрим пример использования преобразования Лапласа для вычисления выхода системы при известном входном сигнале. Пусть объект управления описывается уравнением первого порядка:
и на его вход поступает единичный ступенчатый сигнал $x(t)=1(t)$. Требуется найти сигнал выхода $y(t)$, который в данном случае представляет собой переходную характеристику.
Решим эту задачу с помощью передаточных функций и изображений сигналов по Лапласу. Чтобы найти изображение выхода, нужно знать изображение входного сигнала $X(s)$ и передаточную функцию звена $W(s)$. Изображения находим по табличным данным, повторяя приведенные выше рассуждения:
Теперь находим изображение выхода
Вычисляем оригинал – сигнал выхода:
Обратное преобразования Лапласа:
$$y(t)=-k·\left (exp\left (\frac<-t>
Таким способом можно вычислять реакцию системы на известный входной сигнал без прямого решения дифференциального уравнения.
Вычислим начальное и конечное значение сигнала выхода $y(t)$:
Значение $W(0)$ называют статическим коэффициентом усиления звена, поскольку он показывает, во сколько раз усиливается постоянный сигнал.
Переходная функция
Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент $t=0$. Формально этот сигнал определяется так:
$$1(t)=\begin 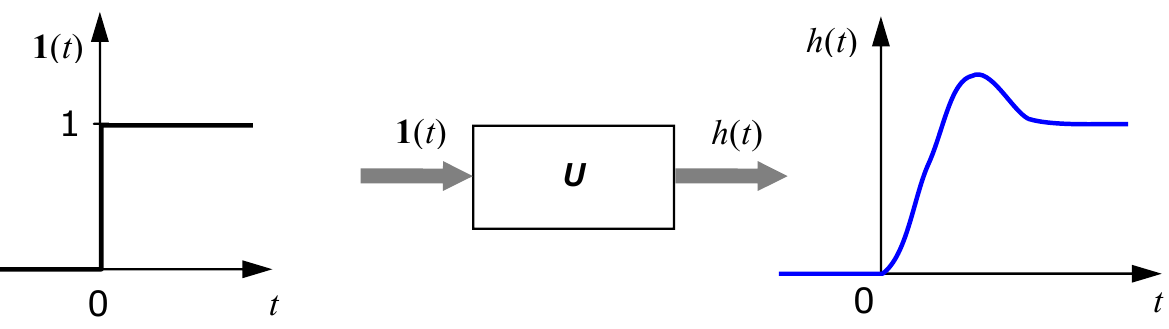
При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.
Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.
Пусть модель объекта задана дифференциальным уравнением первого порядка
где $k$ – безразмерный коэффициент, а $T$ – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение при $x(t)=1(t)$, получаем
где постоянная $C_1$ должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть $y(0)=0$, что дает $C_1=-k$ и поэтому
На рисунке показаны переходные характеристики модели при различных значениях параметра $T$, который называется постоянной времени звена.
Видно, что при увеличении $T$ выход $y(t)$ медленнее достигает установившегося значения, равного $k$, то есть постоянная времени характеризует инерционность звена. Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.
Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.
Импульсная характеристика (весовая функция)
В качестве тестового сигнала можно, в принципе, использовать любой сигнал. Например, можно изучать реакцию системы на прямоугольный импульс. Вопрос в том, чтобы определить некоторый стандартный вид этого импульса. На рисунке показаны три импульса, имеющих одинаковые площади. Для простоты будем считать, что эта площадь равна единице.
Что будет, если мы будем уменьшать ширину импульса, сохраняя его площадь? Очевидно, что высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Таким образом, мы получили еще один классический тестовый сигнал – единичный импульс или дельта-функцию Дирака $δ(t)$. Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме $t=0$, где он уходит к бесконечность, причем его площадь (интеграл по всей оси времени) равен единице:
Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице.
Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала $1(t)$. Действительно, эта производная равна нулю при всех значениях $t$, кроме нуля, где она обращается в бесконечность.
Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикой и обозначается $w(t)$:
Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.
Рассматривая дельта-функцию как предельный случай прямоугольного сигнала единичной площади, можно найти связь между переходной функцией и импульсной характеристикой.
Пусть ширина прямоугольного импульса равна $ε$, а высота – $\frac<1><ε>$ . Такой импульс можно представить в виде разности двух ступенчатых сигналов
где $1(t-ε)$ – это единичный ступенчатый сигнал, который приходит в момент $t=ε$, то есть, смещен по времени на $ε$.
Так как для линейных систем справедлив принцип суперпозиции, сигнал на выходе будет равен разности реакций системы на входы $1(t)$ и $1(t–ε)$, умноженной на коэффициент $\frac<1><ε>$. Учитывая, что реакция на сигнал $1(t)$ – это переходная функция $h(t)$, получаем
Переходя к пределу при $ε→0$, находим, что импульсная характеристика
как оказывается, равна производной от переходной функции. Наоборот, переходная функция – это интеграл от импульсной характеристики на интервале от 0 до $t$:
Дифференцируя переходную характеристику звена первого порядка, получаем соответствующую импульсную характеристику:
Другое название импульсной характеристики – весовая функция. Это название связано с тем, что для произвольного входного сигнала $x(t)$ выход системы $y(t)$ при нулевых начальных условиях вычисляется как интеграл
Здесь функция $w(t)$ как бы «взвешивает» входной сигнал $x(t)$ в подынтегральном выражении.
Заметим, что импульсная характеристика дает неполную информацию об объекте, поскольку не учитывает ненулевые начальные условия.
В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы, строго говоря, экспериментально не удается.
Частотные характеристики
Еще один популярный эталонный сигнал – гармонический (синус, косинус), например:
где $ω$ – угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших $t$) будет синус той же частоты, но с другой амплитудой $A$ и сдвигом фазы $φ$:
Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг $φ$, нужно найти расстояние $∆t$ по оси времени между соответствующими точками синусоид (например, точками пересечения с осью $t$ или вершинами). Если $∆t$ умножить на частоту $ω$, получаем сдвиг фазы $φ$ (в радианах).
На рисунке показан случай $φ>0$ (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного.
Зная передаточную функцию системы $W(s)$, можно вычислить амплитуду и сдвиг фазы по формулам
Запись $W(jω)$ означает, что в передаточную функцию $W(s)$ подставляется чисто мнимое число $s=jω$, где $j=\sqrt<-1>$. Для каждой частоты ω значение $W(jω)=P+jQ$ – это некоторое комплексное число, имеющее амплитуду
Функция $W(jω)$ называется частотной характеристикой звена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости $P(ω)$ и $Q(ω)$ – это вещественная и мнимая частотные характеристики.
Функции $A(ω)$ и $φ(ω)$ называются соответственно амплитудной и фазовой частотными характеристиками (АЧХ и ФЧХ). Амплитудная частотная характеристика – это коэффициент усиления гармонического сигнала. Если на какой-то частоте ω значение $A(ω)>1$, входной сигнал усиливается, если $A(ω) 
В радиотехнике используется понятие полосы пропускания – это ширина полосы частот, в которой значение АЧХ больше, чем $\frac<1><\sqrt<2>>$ от ее максимального значения.
Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал и записывается сигнал $y(t)$ на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики.
Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2022. All rights reserved.
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
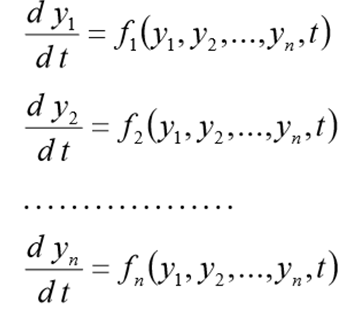
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши


по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 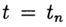

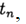


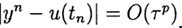


При 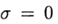
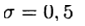
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
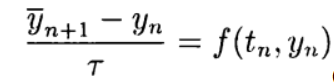
а на этапе корректора (уточнения) — схема
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
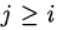

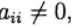
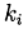
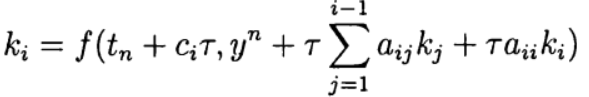
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 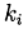
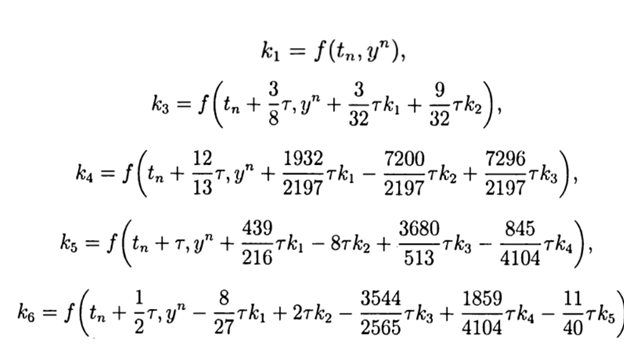
С учётом(9) общее решение имеет вид:
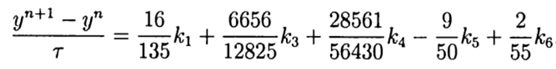
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
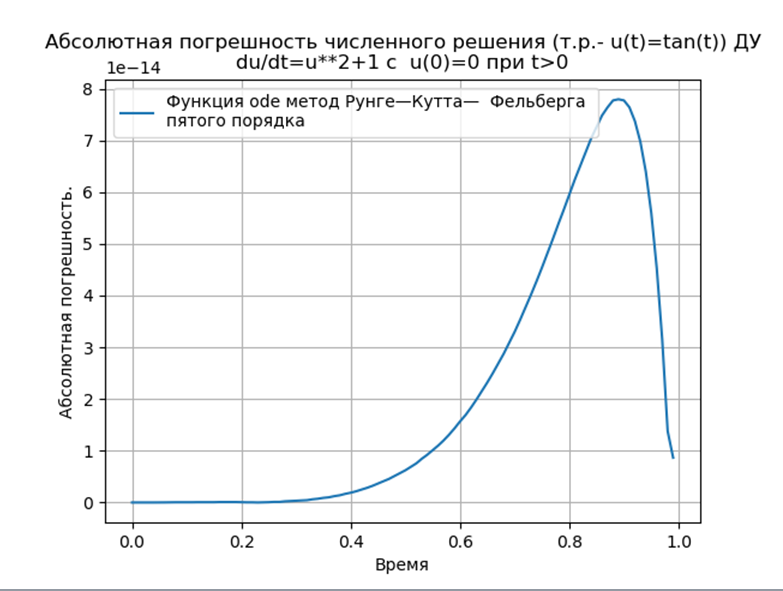
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
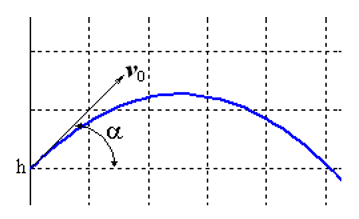
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 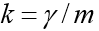
К системе следует добавить начальные условия: 

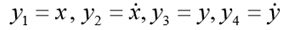
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
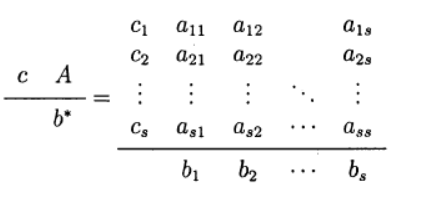
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
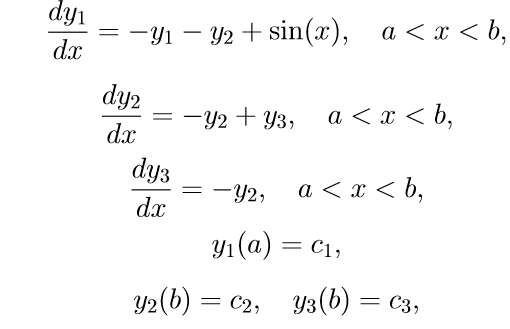
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 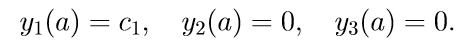
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 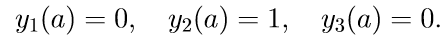
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 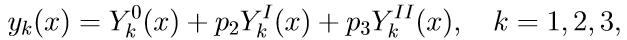
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Составление математической модели
ВВЕДЕНИЕ
Основные понятия и определения
Объект управления – техническое устройство или процесс, поведение которого необходимо изменить.
Управление — процесс воздействия на объект управления с целью изменения его поведения.
Регулирование — частный случай управления, целью которого является приведение состояния объекта к заданному.
Автоматический процесс — процесс, который совершается без участия человека.
Управляющее устройство (регулятор) — устройство, предназначенное для реализации процесса управления (регулирования).
Система — совокупность элементов, объединенных общим режимом функционирования.
Динамическая система – это система, в которой процессы изменяются во времени.
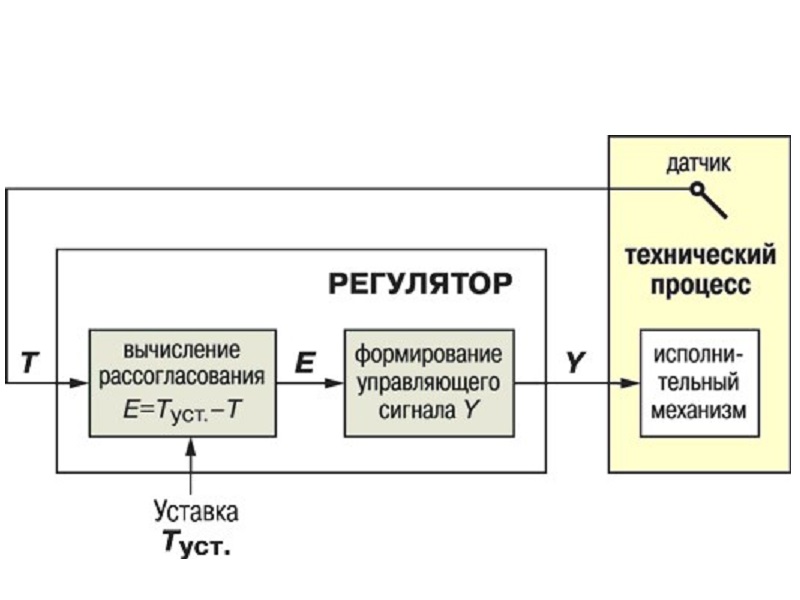
Совокупность объекта управления и управляющего устройства (регулятора) называется системой автоматического управления (регулирования).
Теория автоматического управления (ТАУ) — научно-техническая дисциплина, в рамках которой изучаются свойства систем автоматического управления и разрабатываются принципы их построения и расчета.
Основными элементами САУ являются:
— объект управления (ОУ);
— управляющее устройство или регулятор (Р), который сравнивает выход управляемого объекта с желаемым и в зависимости от этого вырабатывает управляющий сигнал на объект.
Рис.1.1. Функциональная схема замкнутой системы
Рассмотрим подробнее объект управления и выделим переменные, которые его характеризуют.
 Рис.1.2. Функциональная схема объекта управления Рис.1.2. Функциональная схема объекта управления | — Управляющие воздействияu1, . , um — это входные сигналы объекта управления, с помощью которых можно влиять на режим работы объекта. — Входными (задающими) принято называть воздейсвия (сигналы), поступающие на вход системы и определяющие требуемые законы изменения выходных переменных (сигналов) |
— Выходные переменные y1, . , ym — это измеряемые выходные сигналы динамической системы.
— Переменные состояния x1, . , xn — это внутренние, как правило, недоступные измерению переменные, которые определяют состояние объекта в каждый момент времени; причем 
— Возмущающие воздействия M1, . Ml — отражают случайные воздействия окружающей среды на объект управления и обычно недоступны измерению. Требование парирования их влияния и приводит к необходимости создания систем автоматического управления.
Все переменные, которые характеризуют объект, удобно представить в векторной форме:
Входные воздействия на систему (или задание на регулятор) принято обозначать буквой v. Их число обычно совпадает с числом выходных переменных и изображается следующим вектором:
В зависимости от числа входных и выходных переменных выделяют:
— одноканальные объекты (или системы) — объекты, в которых есть только одна выходная переменная (m=1);
— многоканальные (многосвязные, многомерные, взаимосвязные) объекты (или системы) — объекты, в которых число выходных переменных больше единицы (m>1).
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ЛИНЕЙНЫХ СИСТЕМ
Под динамической характеристикой (математической моделью) системы понимают любое соотношение, заданное аналитически, графически или в виде таблицы, которое позволяет рассчитать поведение системы во времени.
2.1. Дифференциальные уравнения
2.2. Составление математической модели
2.3. Структурные схемы
2.4. Переходная функция (переходная характеристика)
2.5.Импульсная функция (импульсная характеристика)
2.6. Переходная матрица
2.7. Передаточная функция
2.8. Модальные характеристики
2.9. Частотные характеристики
Дифференциальные уравнения
Наиболее часто в качестве математической модели объекта управления используются обыкновенные дифференциальные уравнения, которые могут быть записаны в различной форме.
Линейные многоканальные объекты обычно описывают системой дифференциальных уравнений первого порядка, представленной в векторно-матричном виде:
 . . | (2.1) |
Здесь 


Выходные переменные объекта изменяются в соответствии с уравнением выхода
| y = Cx | (2.2) |
где 
Уравнения (2.1) и (2.2) описывают линейный стационарный объект. Если его параметры меняются с течением времени, то такой объект называется нестационарным, а математическая модель имеет вид (2.1)-(2.2), где элементы матриц являются функциями времени: A=A(t); B=B(t); C=C(t).
Для описания одноканального объекта обычно используется скалярное дифференциальное уравнение:
 , , | (2.3) |
которое также может быть приведено к описанию типа (2.1) и (2.2) после соответствующего выбора линейно-независимых переменных состояния. Их число всегда равно порядку объекта (n), а 

Наиболее простое (каноническое) описание получается в случае, когда в качестве переменных состояния выбирается выходная переменная y и ее производные до (n-1) включительно
При этом вместо (2.3) имеем систему уравнений в виде нормальной формы Коши,
 | (2.4) |
которая соответствует векторно-матричным уравнениям (2.1) и (2.2). Здесь матрицы A, B и C имеют вид:
причем
Переход к описанию (2.1) — (2.2) не является однозначным: для одного объекта можно выбрать множество переменных состояния; важно, чтобы они были линейно — независимыми. При этом будут получаться различные матрицы объекта A, B и C.
Записать уравнения состояния одноканального объекта, модель которого имеет вид
1) Если в качестве переменных состояния выбрать выходную величину и ее производную, 
2) Выбирая переменные состояния следующим образом: 
В общем случае одноканальный объект может описываться дифференциальным уравнением вида:
 | (2.5) |
от которого также можно перейти к векторно-матричным уравнениям типа (2.1) — (2.2). Рассмотрим этот переход на примере.
Записать уравнения состояния объекта с математической моделью вида
Выбираем переменные состояния 
Таким образом, в качестве динамической характеристики линейных объектов управления используются дифференциальные уравнения, которые могут быть представлены в форме (2.1) — (2.2), (2.3), (2.4) или (2.5).
Структурные схемы
Структурной схемой называется графическая модель системы, в которой каждому элементу ставится в соответствие его динамическая характеристика.
Рассмотрим, как получить структурную схему, соответствующую векторно-матричному описанию объекта типа:
 | (2.6) |
Проинтегрируем уравнение состояния и определим x(t)
 | (2.7) |
По выражению (2.7) изобразим структурную схему, придерживаясь следующего правила: входные и выходные переменные объекта необходимо располагать на одной горизонтальной прямой.
Рис.2.2. Структурная схема, соответствующая уравнениям состояния объекта
Для одноканального объекта структурную схему можно составить по уравнению (2.3), разрешив его относительно старшей производной
и далее n-раз интегрируя. В результате получим
Рис.2.3. Структурная схема, соответствующая скалярному
дифференциальному уравнению.
Переходная матрица
Эта характеристика применяется для описания многоканальных систем вида (2.1) — (2.2) при нулевых входных воздействиях, то есть для автономных систем типа:
   . . | (2.12) |
Переходная матрица — это решение матричного дифференциального уравнения
 | (2.13) |
при нулевых входных воздействиях и единичных начальных условиях

Она обладает следующими свойствами:
 для любого для любого   | (2.14) |
Зная переходную матрицу, можно определить реакцию системы
на произвольное входное воздействие при любых начальных условиях x(0) по выражению
 . . | (2.15) |
Здесь первое слагаемое — свободная составляющая движения, второе — вынужденная. Для выходных переменных имеем
 | (2.16) |
Если система имеет нулевые начальные условия x(0)=0, то
 , , | (2.17) |
 . . | (2.18) |
Матрица 

Для многоканальных систем может быть определена также матричная переходная характеристика в виде
 | (2.19) |
Для линейных систем с постоянными параметрами переходная матрица Ф(t) представляет собой матричную экспоненту
 | (2.20) |
где
С учетом (2.20) выражения (2.15) и (2.16) принимают вид
 | (2.21) |
 | (2.22) |
Матричная импульсная функция линейной системы с постоянными коэффициентами следующая:
 | (2.23) |
При небольших размерах или простой структуре матрицы A выражение (2.20) может быть использовано для точного представления переходной матрицы с помощью элементарных функций. В случае большой размерности матрицы A следует использовать существующие программы для вычисления матричного экспоненциала.
Передаточная функция
Наряду с обыкновенными дифференциальными уравнениями в теории автоматического управления используются различные их преобразования. Для линейных систем эти уравнения удобнее записывать в символической форме с использованием так называемого оператора дифференцирования

что позволяет преобразовывать дифференциальные уравнения как алгебраические и ввести новую динамическую характеристику — передаточную функцию.
Рассмотрим этот переход для многоканальных систем вида (2.6)

Запишем уравнение состояния в символической форме:
что позволяет определить вектор состояния
 | (2.24) |
и выходные переменные системы
 | (2.25) |
Матрица взаимосвязи между выходными переменными и управляющими воздействиями в выражении (2.25) при нулевых начальных условиях называется матричной передаточной функцией и обозначается
 | (2.26) |
Она представляет собой матрицу со следующими компонентами:
 | (2.27) |
где 
Собственными передаточными функциями i-го канала называются компоненты передаточной матрицы 
Обратная матрица 
 | (2.28) |
где 
Если теперь характеристический полином приравнять нулю, то получим характеристическое уравнение системы,
| A(p) = det(pI-A) = 0. | (2.29) |
Определить передаточную матрицу для объекта
где
Воспользуемся выражением для передаточной матрицы (2.27) и найдем предварительно обратную матрицу (2.29). Здесь
Транспонированная матрица имеет вид

где 
и передаточную матрицу объекта
Чаще всего передаточные функции применяются для описания одноканальных систем вида
 | (2.30) |
Используя оператор дифференцирования, запишем уравнение (2.30) в символической форме и найдем передаточную функцию как отношение выходной величины к входной:
 , , | (2.31) |
где 
Передаточные функции принято записывать в стандартной форме:
 , , | (2.32) |
где 
Передаточную матрицу (передаточную функцию) можно также определить с помощью изображений Лапласа или Карсона-Хевисайда. Если подвергнуть одному из этих преобразований обе части дифференциального уравнения и найти соотношения между входными и выходными величинами при нулевых начальных условиях, то получим ту же самую передаточную матрицу (2.26) или функцию (2.31).
Для того, чтобы в дальнейшем различать преобразования дифференциальных уравнений, будем использовать следующие обозначения:


Получив одну из динамических характеристик объекта, можно определить все остальные. Переход от дифференциальных уравнений к передаточным функциям и обратно осуществляется с помощью оператора дифференцирования p.
Рассмотрим взаимосвязь между переходными характеристиками и передаточной функцией. Выходная переменная находится через импульсную функцию в соответствии с выражением (2.10),
Подвергнем его преобразованию Лапласа,

и получим y(s) = g(s)u(s). Отсюда определим импульсную функцию:
 | (2.33) |
Таким образом, передаточная функция — есть преобразование по Лапласу от импульсной функции.
Определить передаточную функцию объекта, дифференциальное уравнение которого имеет вид
Используя оператор дифференцирования d/dt = p, запишем уравнение объекта в символической форме
на основании которого определим искомую передаточную функцию объекта
Модальные характеристики
Модальные характеристики соответствуют свободной составляющей движения системы (2.6) или, другими словами, отражают свойства автономной системы типа (2.12)
 | (2.34) |
Будем искать ее решение в виде экспоненты
 | (2.35) |
где 

Подставляя решение (2.35) в исходное уравнение (2.34), после преобразований получим
 . . | (2.36) |
Система уравнений (2.36) будет иметь ненулевое решение относительно 
 . . | (2.37) |
Уравнение (2.37) называется характеристическим и имеет n-корней 

где 
Совокупность собственных значений и собственных векторов представляет собой модальные характеристики системы.
Для (2.34) могут существовать лишь следующие экспоненциальные решения
 | (2.38) |
которые называют модами. В случае, когда собственные значения вещественные и различные по значениям, полное решение системы (2.34) представляет собой линейную комбинацию мод:
 . . | (2.39) |
Для получения характеристического уравнения системы достаточно общий знаменатель передаточной матрицы (передаточной функции) приравнять нулю (2.29).
Частотные характеристики
Если на вход объекта подавать периодический сигнал заданной амплитуды и частоты, то на выходе будет также периодический сигнал той же частоты, но в общем случае другой амплитуды со сдвигом по фазе. Взаимосвязь между параметрами периодических сигналов на входе и выходе объекта определяют частотные характеристики. Чаще всего их используют для описания одноканальных систем:
 , n >= m. , n >= m. | (2.40) |
Формально обобщенная частотная характеристика 
 | (2.41) |
и представлена в виде
   . . | (2.42) |
Составляющие обобщенной частотной характеристики 
вещественная частотная характеристика (ВЧХ),
мнимая частотная характеристика (МЧХ),
амплитудная частотная характеристика (АЧХ),
фазовая частотная характеристика (ФЧХ).
Частотная характеристика 



Рис.2.6. Пример амплитудно-фазовой характеристики системы
Фазо-частотная характеристика (ФЧХ) — графическое отображение зависимости сдвига по фазе между входным и выходным сигналами в зависимости от частоты,
Для определения 


тогда 
Каждое из слагаемых 
где 
Наряду с АФХ отдельно строят и все остальные частотные характеристики. Так АЧХ показывает, как пропускает звено сигнал различной частоты; причем оценкой пропускания является отношение амплитуд выходного и входного сигнала. ФЧХ показывает фазовые сдвиги, вносимые системой на различных частотах.
Помимо рассмотренных частотных характеристик в теории автоматического управления используются логарифмические частотные характеристики. Удобство работы с ними объясняется тем, что операции умножения и деления заменяются на операции сложения и вычитания. Построенная в логарифмическом масштабе АЧХ, называется логарифмической амплитудной частотной характеристикой (ЛАЧХ)
 , , | (2.43) |
Эта величина выражается в децибелах (дб). При изображении ЛАЧХ удобнее по оси абсцисс откладывать частоту в логарифмическом масштабе, то есть 
Рис.2.7. Пример логарифмической амплитудной частотной характеристики
В логарифмическом масштабе может быть изображена также и ФЧХ:
Рис.2.8. Пример логарифмической фазовой частотной характеристики
ЛФХ, реальная и асимптотическая ЛАЧХ системы, передаточная функция которой имеет вид:
 . . | (2.44) |

Рис. 2.9. Реальная и асимптотическая ЛАЧХ системы

Рис. 2.10. ЛФХ системы
СТРУКТУРНЫЙ МЕТОД
3.2. Пропорциональное звено (усилительное, безынерционное)
3.3. Дифференцирующее звено
3.4. Интегрирующее звено
3.5. Апериодическое звено
3.6. Форсирующее звено (пропорционально — дифференцирующее)
3.7. Звено 2-го порядка
3.8. Структурные преобразования
3.8.1. Последовательное соединение звеньев
3.8.2. Параллельное соединение звеньев
3.8.3. Обратная связь
3.8.4. Правило переноса
3.9. Переход от передаточных функций к уравнениям состояния с пользованием структурных схем
3.10. Область применимости структурного метода
Введение
Для расчета различных систем автоматического управления их обычно разбивают на отдельные элементы, динамическими характеристиками которых являются дифференциальные уравнения не выше второго порядка. Причем различные по своей физической природе элементы могут описываться одинаковыми дифференциальными уравнениями, поэтому их относят к определенным классам, называемым типовыми звеньями.
Изображение системы в виде совокупности типовых звеньев с указанием связей между ними называется структурной схемой. Она может быть получена как на основе дифференциальных уравнений (раздел 2), так и передаточных функций. Данный способ и составляет суть структурного метода.
Предварительно рассмотрим подробнее типовые звенья, из которых состоят системы автоматического управления.
Пропорциональное звено
(усилительное, безынерционное)
Пропорциональным называется звено, которое описывается уравнением
| y = k u. | (3.1) |
Передаточная функция звена следующая:
 , , | (3.2) |
а соответствующая ей структурная схема приведена на рис. 3.1.
 Рис.3.1. Структурная схема пропорционального звена Рис.3.1. Структурная схема пропорционального звена | Переходная характеристика (реакция звена на скачкообразное входное воздействие) имеет вид: h(t) = k  1(t) . 1(t) . |
Импульсная функция имеет вид:
g(t) = k 
Модальные характеристики (собственные значения и собственные векторы) для пропорционального звена отсутствуют.
Заменив в передаточной функции p на j 
 Рис.3.2 ВЧХ пропорционального звена Рис.3.2 ВЧХ пропорционального звена | — амплитудно-фазовую: W (j  ) k , — вещественную частотную характеристику: R( ) k , — вещественную частотную характеристику: R(  )=k , — мнимую частотную характеристику, I( )=k , — мнимую частотную характеристику, I(  )=0 . )=0 . |
Амплитудная частотная характеристика (АЧХ) определяется соотношением:
 | (3.3) |
и имеет тот же вид, что и ВЧХ. Выражение для ФЧХ:
 . . | (3.4) |
Это означает, что амплитуда периодического входного сигнала усиливается в k — раз, а фазовый сдвиг отсутствует.
 Рис.3.3 АФХ пропорционального звена Рис.3.3 АФХ пропорционального звена | АФХ звена имеет вид точки на комплексной плоскости (рис. 3.3). ЛАЧХ звена представляет собой прямую, параллельную оси абсцисс: |
L(  )=20lg[A( )=20lg[A(  )]=20lg(k) )]=20lg(k) | (3.5) |
 Рис.3.4 ЛАЧХ пропорционального звена Рис.3.4 ЛАЧХ пропорционального звена | Как видим (3.3.), (3.4.), пропорциональное звено пропускает входные сигналы без искажений. |
Дифференцирующее звено
Дифференцирующим называется звено, которое описывается дифференциальным уравнением:
y = k  . . | (3.6) |
Его передаточная функция имеет вид:
| W(p) = y(p)/u(p) = kp. | (3.7) |
 Рис.3.5. Переходная характеристика звена Рис.3.5. Переходная характеристика звена | Переходная характеристика дифференцирующего звена: h(t) = k  (t- (t-  ). ). |
 Рис.3.6. Импульсная характеристика Рис.3.6. Импульсная характеристика | Импульсная функция имеет вид
Получим теперь частотные характеристики звена. АФХ : W(j ВЧХ : R( МЧХ : I( АЧХ : ФЧХ :
|
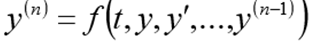
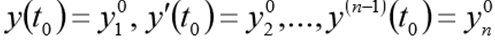


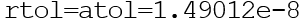
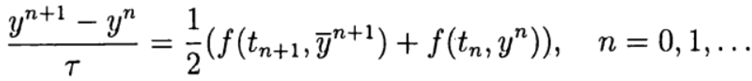
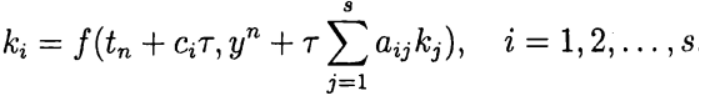
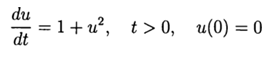 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга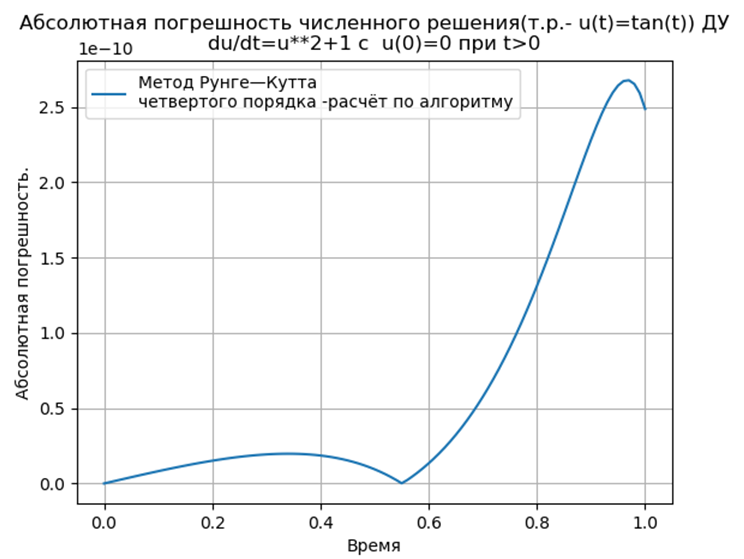



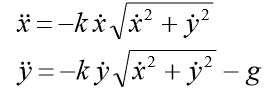




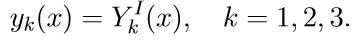
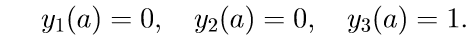
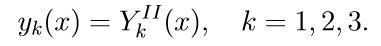





































 вещественная частотная характеристика (ВЧХ),
вещественная частотная характеристика (ВЧХ), мнимая частотная характеристика (МЧХ),
мнимая частотная характеристика (МЧХ), амплитудная частотная характеристика (АЧХ),
амплитудная частотная характеристика (АЧХ), фазовая частотная характеристика (ФЧХ).
фазовая частотная характеристика (ФЧХ).




 (t-
(t-  ) = j k
) = j k  ,
, ,то есть для всех частот звено вносит постоянный фазовый сдвиг;
,то есть для всех частот звено вносит постоянный фазовый сдвиг; Рис.3.7. ЛАЧХ дифференцирующего звена
Рис.3.7. ЛАЧХ дифференцирующего звена )=20lg(k
)=20lg(k  .
. ,
, .
. ,
, .
.
 ; ВЧХ:
; ВЧХ:  ; МЧХ:
; МЧХ:  ;
; ;
; .
. Рис.3.9. ЛАЧХ интегрирующего звена
Рис.3.9. ЛАЧХ интегрирующего звена
 , который представляет собой модальную характеристику интегрирующего звена.
, который представляет собой модальную характеристику интегрирующего звена. .
. ,
, ,
,  — коэффициент передачи звена.
— коэффициент передачи звена. .
. Рис.3.10. Переходная характеристика
Рис.3.10. Переходная характеристика )·1(t).
)·1(t). Рис.3.11. Импульсная функция
Рис.3.11. Импульсная функция (t)=
(t)=  ·1(t).
·1(t).