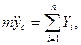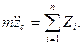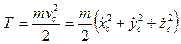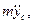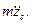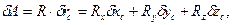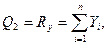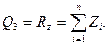Дифференциальные уравнения поступательного движения
Основные задачи динамики твердого тела
В статике были рассмотрены условия равновесия системы сил, приложенных к абсолютно твердому телу и условия, при которых твердое тело находится в покое. Задание уравнений движения твердого тела и определение скоростей и ускорений точек твердого тела было рассмотрено в кинематике. При решении задач динамики твердого тела встают более сложные задачи, которые делятся на две основные группы. К первой группе относятся задачи, в которых по заданным уравнениям движения твердого тела требуется определить систему сил, под действием которых происходит это движение. Ко второй относятся задачи, в которых по заданным силам, действующим на тело, требуется при определенных начальных условиях найти уравнения движения тела, а для несвободного тела найти также реакции связей.
Рассмотрим движение твердого тела в плоскости. Для определения его положения требуется задать три независимых между собой параметра. Обычно это координаты центра масс 






Движение тела в плоскости обычно раскладывают на простейшие: поступательное движение тела, задаваемое уравнениями движения центра масс 

Для получения законов движения воспользуемся теоремой о движении центра масс и теоремой об изменении кинетического момента.
Согласно теореме о движении центра масс (3.6), имеем


Здесь m – масса тела, 
Используя теорему об изменении кинетического момента относительно оси О z, перпендикулярной плоскости вращения Оху (3.18, а), имеем
Здесь 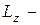

Итак, законы движения тела в плоскости имеют вид


Дифференциальные уравнения поступательного движения
твердого тела
Для того, чтобы твердое тело двигалось поступательно, линия действия главного вектора внешних сил должна проходить через центр масс тела. Тогда угловая скорость и, соответственно, кинетический момент тела равны нулю.
Пусть тело движется поступательно, уравнения движения имеют вид: 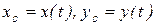


Дифференциальный закон (4.2) имеет форму закона движения материальной точки в плоскости и в общем случае позволяет решить две основные задачи динамики:
· первая задача: по заданным уравнениям движения центра масс 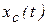



· вторая задача: по заданным 





Дифференциальные уравнения поступательного движения твердого тела

Дифференциальные уравнения поступательного движения твердого тела
- Из теоремы о движении центра тяжести системы получаем дифференциальное уравнение для поступательного движения твердого тела. У нас есть L / ac = EAe). Однако при перемещении твердого тела ускорение во всех точках тела одинаково по модулю и направлению, то есть ac — a.
Некоторые представления о напряженном состоянии системы в заданном направлении можно вывести из силы смещения, которую можно назвать коэффициентом жесткости в заданном положении. Людмила Фирмаль
Где a — ускорение в любой точке тела. Учитывая это, из теоремы о движении центра тяжести получено следующее дифференциальное уравнение для поступательного движения тела в векторной форме: AW-Å † Когда проецируется на оси, это выглядит так: Mx = EFL; My = bFly, Mz = ZFL.
- Это дифференциальные уравнения для поступательного движения твердого тела в проекции на декартовы оси. В этих уравнениях x, y и z являются координатами любой точки на теле, в частности, они являются координатами их центроидов. Поскольку поступательный объект имеет три степени свободы, он может составлять три дифференциальных уравнения движения.
Полное решение этой системы обыкновенных неоднородных линейных дифференциальных уравнений с постоянным коэффициентом состоит из общего решения однородных систем, полученного в задаче 18. Людмила Фирмаль
Дифференциальное уравнение для поступательного движения твердого тела аналогично дифференциальному уравнению для движения одной материальной точки. Эти уравнения могут быть использованы для решения той же проблемы, что и одна точка.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Дифференциальные уравнения поступательного движения твердого тела
Пусть тело под действием приложенных к нему сил движется поступательно. Применяя теорему о движении центра масс (центра инерции), можно получить дифференциальные уравнения поступательного движения тела. Действительно, по (111.65),
где m — масса тела;ωc= rc— ускорение его центра инерции, R — главный вектор внешних сил, приложенных к телу.
В проекциях на оси координат получим
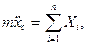
Интегрируя эти уравнения, можно определить координаты центра инерции тела как функции времени. Постоянные интегрирования определяются из начальных условий движения (при t=t0:

Указанные уравнения можно также получить исходя из уравнений Лагранжа второго рода.
Обозначим координаты центра инерции твердого тела через хc, уc, zc и примем их за обобщенные координаты:
Поступательное движение тела полностью определяется движением его центра инерции, а поэтому число степеней свободы тела равно трем (k =3) и уравнения Лагранжа второго рода в этом случае будут иметь вид
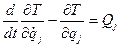
Кинетическая энергия тела равна
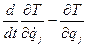
соответственно равны 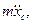
найдем обобщенные силы Qj (j=1, 2, 3):
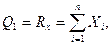
Составляя уравнения Лагранжа, получим уравнения (111.217).
http://lfirmal.com/differencialnye-uravneniya-postupatelnogo-dvizheniya-tverdogo-tela/
http://helpiks.org/4-64514.html