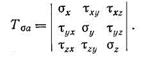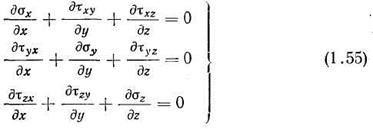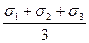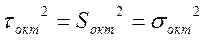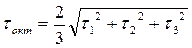Дифференциальные уравнения равновесия для осесимметричного напряженного состояния
Решение дифференциальных уравнений равновесия совместно с условием пластичности
Этот метод заключается в совместном решении системы из дифференциальных уравнений равновесия и уравнения, выражающего условие пластичности. Уравнения пишут в форме (для объемного, осесимметричного, плоского напряженного состояний, плоского деформированного состояния) и в координатах (прямоугольных, цилиндрических, полярных, сферических), отвечающих условиям рассматриваемой конкретной задачи.
Произвольные постоянные определяют из граничных условий. При наличии трения необходимо задать условия трения, определяющие касательные напряжения на поверхностях контакта. Условия трения принимают практически только в двух формах: либо контактные касательные напряжения считают независимыми от координаты, по которой они направлены, т. е. постоянными [см. выражение (5.46)], либо их считают пропорциональными нормальным напряжениям на поверхности контакта. Если задача представляется статически неопределимой, то дополнительно используют уравнения-связи между напряжениями и деформациями и уравнения неразрывности деформаций.
Решение в принципе должно дать величину и распределение напряжений по всему объему тела, т. е. значения напряжений как функции координат точек тела, в том. числе и. лежащих на поверхности, непосредственно воспринимающей, активное усилие. К сожалению, такое решение возможно лишь в отдельных частных случаях и то при отсутствии (или в предположении отсутствия) сил трения на контактных поверхностях.
Разберем теперь возможности решения дифференциальных уравнений равновесия для ^различных видов пластически напряженного состояния.
При объемном напряженном состоянии мы располагаем тремя уравнениями равновесия (3.38), в которые входят шесть неизвестных (три нормальных и три касательных напряжения) и условие пластичности (5.5), заключающее те же неизвестные. В этом случае в четырех уравнениях шесть неизвестных, и задача дважды статически неопределима. Дополнительно можно использовать уравнения связи между напряжениями и деформациями и уравнения неразрывности деформаций, которые внесут, однако, новые неизвестные (шесть деформаций и модуль пластичности). В результате можно получить 13 уравнений с 13 неизвестными [3]. Однако, несмотря на то, что количество неизвестных будет соответствовать числу уравнений, практически решение этой системы невозможно. Таким образом, объемная задача в общем виде (шесть напряжений, каждое из которых есть функция трех координат) является пока неразрешимой. Для осесимметричного напряженного состояния есть два уравнения равновесия (3.39), содержащие четыре неизвестных, и условие пластичности (5.14), в которое входят те же неизвестные. Таким образом, осесимметричная задача так же, как и объемная, статически неопределима, и для решения ее требуется привлечение уравнений связи между напряжениями и деформациями (четыре уравнения, которые внесут четыре новых неизвестных) и уравнение совместимости деформаций. Всего получим восемь уравнений с восемью неизвестными. Отсюда следует, что осесимметричная задача значительно проще объемной. Однако точные замкнутые решения этой задачи существуют только для отдельных частных случаев, когда касательное напряжение на контактной поверхности или отсутствует, или зависит только от одной из двух координат, входящих в условия равновесия.
Для плоского напряженного и плоского деформированного состояний располагаем двумя уравнениями равновесия (3.50) в декартовых координатах или (3.51) в полярных координатах и условием пластичности (5.10) или (5.12). В этих трех уравнениях содержится три неизвестных. Таким образом, число уравнений соответствует числу неизвестных. Тем не менее для системы уравнений этой задачи существуют точные замкнутые решения тоже лишь для частных случаев при касательных напряжениях на контактной поверхности, равных нулю или не зависящих от одной из двух координат, входящих в уравнения равновесия.
К числу осесимметричных и плоских задач, для которых метод интегрирования дифференциальных уравнений равновесия совместно с условием пластичности дает при вышеуказанных предпосылках точные замкнутые решения, например, относятся: пластическое равновесие толстостенной трубы под действием внутреннего и внешнего давлений (А. Надаи), сжатие бесконечной полосы между шероховатыми плитами при тк = const (Л. Прандтль [103]), сжатие клина, равновесие пластической массы, заполняющей форму конуса (В. В. Соколовский [911), осадка без трения толстостенной трубы, замкнутой в матрицу, и др.
УСЛОВИЯ РАВНОВЕСИЯ ДЛЯ ОБЪЕМНОГО
НАПРЯЖЕННОГО СОСТОЯНИЯ
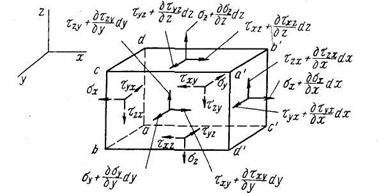
Величина напряжений в теле, нагруженном силами и находящемся в равновесии, в общем случае непрерывно изменяется от точки к точке, т. е. напряжения являются непрерывными функциями координат. Выделим в напряженном теле элементарный параллелепипед (рис. 3.10) с гранями, параллельными координатным плоскостям, и выясним, какие существуют условия, обеспечивающие его равновесие.
Пусть одна из напряженных точек а с координатами х, у, z отображается гранями параллелепипеда abcd, adb’c’ и ac’d’b. Вторая точка 


Рис.3.10. Напряжения на гранях элементарного параллелепипеда
Пусть напряженное состояние точки 
Напряжения в точке 


Усилия, действующие по граням параллелепипеда, равны напряжениям, умноженным на площади соответствующих граней, указываемых индексами адреса напряжения.
Составляем условия равновесия, взяв суммы проекций всех сил на оси координат и приравнивая эти суммы нулю.
Раскрывая скобки и сокращая на dxdydz, получим
Суммы проекций на оси 

В результате получим


Таким образом, мы получили условия равновесия для объемного напряженного состояния в виде дифференциальных уравнений в частных производных.
Эти условия обязательны для всех точек деформируемого тела.
Напряжения меняются по объему тела, и в элементах, выходящих на поверхность, их величина должна быть такой, чтобы уравновешивать внешнюю нагрузку, действующую на поверхностную грань [5], т.е. удовлетворять поверхностным условиям или условиям на контуре.
Связать напряжение в бесконечно малом элементе тела, выходящем на его поверхность, с внешней нагрузкой можно, используя уравнения (3.3). Действительно, в общем случае элементарный участок поверхности тела можно рассматривать как наклонную грань элементарного тетраэдра.
Три дифференциальных уравнения равновесия (3.38) содержат шесть неизвестных (учитывая, что касательные напряжения попарно равны между собой), и, следовательно, для их решения требуются дополнительные уравнения. Таким образом, объемная задача в общем случае является статически неопределимой.
3.11. ОСЕСИММЕТРИЧНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Одним из частных случаев объемного напряженного состояния, весьма часто встречающимся при обработке металлов давлением, является осесимметричное напряженное состояние.
Под этим видом напряженного состояния подразумевается напряженное состояние тела вращения, к поверхности или части поверхности которого приложены распределенные нагрузки, расположенные симметрично относительно его оси и одинаковые во всех меридиональных сечениях (рис. 3.11а). Примерами могут служить осадка цилиндрической заготовки, ее прошивка, выдавливание (прессование), волочение и др.
При рассмотрении осесимметричного напряженного состояния весьма удобно пользоваться взамен декартовых цилиндрическими координатами, в которых положение любой точки А определяется радиусом-вектором 




Тензор напряжений в цилиндрических координатах запишется так:
Рис.3.11. Осесимметричное напряженное состояние
Напряжение 


При осесимметричном напряженном состоянии компоненты напряжений не зависят от координаты 


Рис. 3.12. Форма элемента и напряжения в цилиндрической
Системе координат
Поэтому с учетом закона парности касательных напряжений






Таким образом, компоненты напряжений при осесимметричном напряженном состоянии можно записать так:
Рис. 3.13. Напряжения, действующие на элемент при осесимметричном
Напряженном состоянии
Всего будет три нормальных и два равных между собой касательных напряжения.
Применяя тот же метод, который был использован при рассмотрении объемного напряженного состояния в декартовых координатах (стр. 100), выведем дифференциальные уравнения равновесия в цилиндрических координатах для осесимметричного напряженного состояния.
Действующие напряжения показаны на рис. 3.14. Ось 

Площади элементарных площадок












Запишем условия равновесия, проецируя все действующие на элемент силы на оси



Рис.3.14. Сферическая система координат

После алгебраических преобразований и сокращений, пренебрегая бесконечно малыми высших порядков, получим

При решении некоторых осесимметричных задач в дальнейшем придется встретиться кроме цилиндрических координат со сферическими. В этой системе (рис. 3.15) положение точки определяется радиус-вектором 








При осесимметричном напряженном состоянии напряжения не зависят от координаты 


Дифференциальные уравнения равновесия для осесимметричного напряженного состояния в сферических координатах приведем без вывода:

Дифференциальное уравнение равновесия.
В теле, находящемся в напряженном состоянии, величина напряжений изменяется от точки к точке и является непрерывной функцией координат. Определим условия равновесия бесконечно малого параллелепипеда с ребрами dx, dy и dz, параллельными осям координат х, у, z (рис. 10), не являющимся главными. Напряженное состояние точки а с координатами х, у, z определяется напряжениями, действующими на гранях abcd, adb’c’ и abd’c’, и соответствующим им тензором напряжений:
Напряженное состояние в точке а’ определяется напряжениями, действующими на площадках 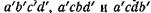
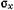
Рис. 11. Напряжения на гранях бесконечно малого параллелепипеда
После раскрытия скобок и сокращения на dxdydz получаем одно из уравнений равновесия. Проектируя силы на оси х, у и z, получаем дифференциальные уравнения равновесия, которые содержат 9 неизвестных функций.
Благодаря свойству взаимности касательных напряжений, число неизвестных функций сокращается до 6 и все же задача определения напряжений является статически неопределимой. Для решения задачи вводят дополнительные уравнения, которые получают из рассмотрения физических свойств деформируемых материалов, в которых установлены зависимости между напряжениями и деформациями.
Дифференциальные уравнения равновесия являются основой при определении компонентов тензора напряжений в рассматриваемой точке пластически деформируемого тела.
ТОМД. Практические занятия по теме «Теория напряжений»
Некоторые понятия и формулы по теме «напряжения»
1) Октаэдрические напряжения .
Наряду с площадями, по которым действует σ и τ в теории ОМД рассматриваются площадки, равнонаклонённые к главным осям и следовательно отсекающие на них отрезки одинаковой длины. Эти площадки называются октаэдрическими. Всего таких площадок 8 , и вместе они образуют октаэдр. Эти площадки попарно взаимно параллельны , поэтому независимых площадок только 4. Напряжения действующие на октаэдрические площадки называют октаэдрическими: полное октаэдрическое напряжение Sокт;нормальное октаэдрическое: σокти касательное октаэдрическоенапряжение τокт.
Sокт= 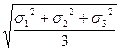
Нормальное октаэдрическое напряжение: σокт = σср =
Октаэдрическое касательное напряжение τокт.
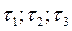
http://zdamsam.ru/a69320.html
http://helpiks.org/3-84927.html