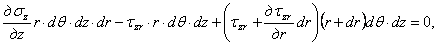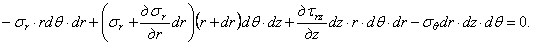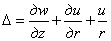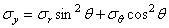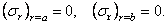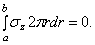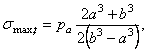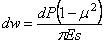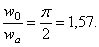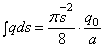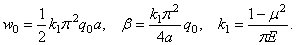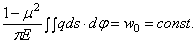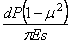Дифференциальные уравнения равновесия в цилиндрической системе координат

Лекция 2. Простейшие осесимметричные задачи

2.1 Уравнения в цилиндрических координатах

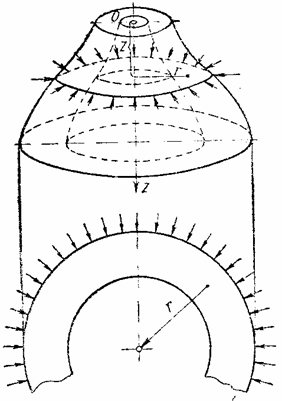
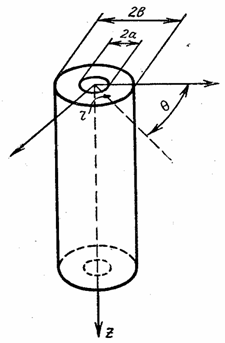
Представим тело вращения, к которому приложены силы, расположенные симметрично относительно оси этого тела (рис.18). Примерами могут быть круглый цилиндр, усеченный конус, деформирующийся под действием равномерного вну­треннего или наружного давления или сил, равномерно приложенных по торцевым сечениям.

За ось вращения примем ось z , ось же перпендикулярную к ней, обозначим через r . Двух координат z и r вполне достаточно, так как все точки с одинаковыми такими коор­динатами находятся в одинаковых условиях.

Так как каждая меридиональная плоскость z 0 r представляет плос­кость симметрии как в отношении формы, так и в отношении нагрузки тела, то в меридиональных плоско­стях касательных напряжений быть не может. Поэтому для каждой точ­ки тела, расположенной на меридиональной плоскости, площадка, содержащая эту точку, является главной площадкой рассматриваемого напряженного состояния. Глав­ное напряжение, действующее по этой площадке, обозначим через .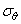

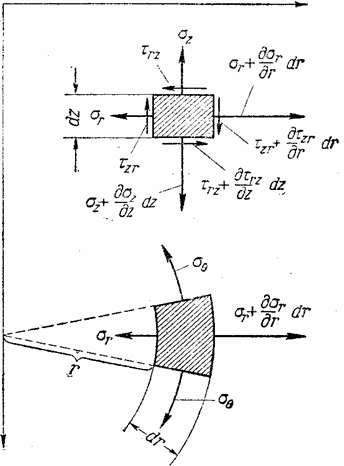
Кроме меридионального сечения через точку с коорди­натами z , r проведем еще второе сечение, перпендикулярное к оси z , и третье сечение, перпендикулярное к двум первым. Следы этих двух секущих плоскостей на меридиональ­ной плоскости будут параллельны соответственно осям r и z .

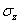
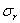
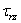
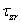
Вследствие симметрии в обеих секущих плоскостях, в точке z , r могут действо­вать лишь такие касательные напряжения, которые парал­лельны меридиональной плос­кости (рис. 19). Нормаль­ные напряжения, действующие в секущих плоскостях, обоз­начим через и , касатель­ные — через и . Эти на­пряжения надо считать функциями от z и r .

Указанные выше условия задачи характеризуют случай, когда основные уравнения упругого равновесия можно представить в такой же про­стой форме, как и в случае плоской задачи, и потому мо­жем ограничиться рассмотре­нием соотношений, имеющих место для точек одной и той же плоскости.

z

Проектируя все усилия, принадлежащие элементарному объему на оси z и r , имеем уравнения равновесия в виде:

После сокращения на общий множитель 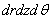статические уравнения запишутся:

(2.1)

Обозначая упругие перемещения точки в направлении оси z через w , в направлении радиуса через и ( в тангенциальном направлении перемещение отсутствует), геометрические уравнения для данного случая можем представить в виде

. (2.2)

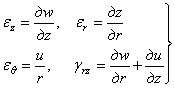
Наконец, физические уравнения, согласно (1.24)

. (2.3)

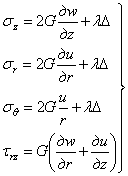
При решении задачи в перемещениях объемное расширение

может быть переписано в виде

, (2.4)

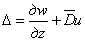
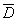
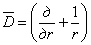
где под надо понимать обозначение следующей операции:

.

Подставляя (2.4) в физические уравнения (2.3), и, далее, в уравнения равновесия (2.1), придаем последним вид

(2.5)

. (2.6)

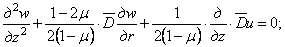
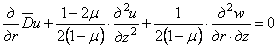
Таким образом, задача определения напряжений в теле вращения, загруженном симметрично относительно оси, сво­дится к нахождению двух функций w и и , которые должны удовлетворять в каждой точке уравнениям (2.5) и (2.6) и одновременно граничным условиям на поверхности тела.

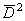
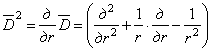
Если, кроме того, ввести оператор , положив

,

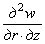
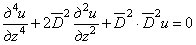
то из уравнений (2.5) и (2.6), исключая из них w , диф­ференцируя (2.5) по z и r и подставляя из (2.6), по­лучим:

. (2.7)

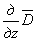
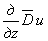
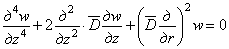
Аналогично можно составить дифференциальное уравнение, которому должно удовлетворять пере­мещение w , если к уравнению (2.6) сначала применить операцию , а затем вставить из уравнения (2.5):

. (2.8)

Установленные уравнения теории упругости в напряжениях (уравнения неразрыв­ности деформаций, выраженные через напряжения), написан­ные в декартовых координатах, можно преобразовать к ци­линдрическим координатам,

Для этой цели надлежит выразить напряжения и через и по известным формулам перехода

;

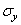
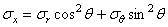
заменив запись суммы другой:

,

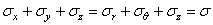
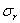
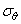
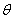
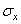
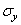
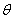
но учесть, что и не зависят от угла , тогда как и являются функциями .

Запишем окончательные резуль­таты для уравнений совместности, которых ввиду осесимметричного характера деформаций останется четыре:

, (2.9)

где введен символ

. (2.10)

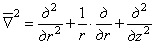
Заметим, что одновременно с уравнениями неразрывности должны быть удовлетворены уравнения равновесия (2.1) и условия на контуре.

Подобно тому, как в плоской задаче теории упругости удалось все компоненты напряжений выразить через одну функцию напряжений, так и в разбираемом осесимметричном пространственном случае имеется такая же возможность.

В самом деле, если задаться

, (2.11)

где — произвольная функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно обратится в тождество. Второе уравнение равновесия и все уравнения неразрывности будут удовлетворены, если принять согласно уравнению

. (2.12)

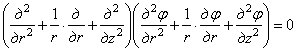
Можно подобрать много решений уравнения (2.12). Вот некоторые из них:

(2.13)

. (2.14)

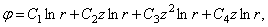
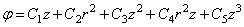
Так как эти выражения удовлетворяют уравнению (2.12) при любых значениях коэффициентов С , следовательно, любой член их также удовлетворяет уравнению (2.12). Например, может быть

. (2.15)

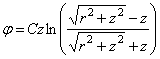
Если в числе прочих причиной, вызывающих напряженное и дефор­мированное состояния тела, является возникновение темпера­турного поля, в общем случае неравномерного вдоль коор­динаты z и вдоль радиуса r , т. е.

то надлежит внести дополнения в физи­ческие уравнения (2.3), а именно, они должны быть запи­саны [(по аналогии с (1.47), но в цилиндрических координа­тах] следующим образом:

(2.16)

(2.17)

(2.18)

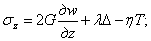
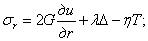
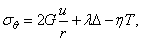
где, введе­но обозначение:

.

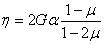
В качестве примера рассмотрим длинную толстостенную трубу (рис. 20) с радиальным перепадом температур, т. е. считается заданным закон Т = Т ( r ).

Пренебрегая влиянием торцов, можно считать, что все сечения трубы, перпендикулярные к ее оси, остаются плоскими и все работают в одинаковых условиях. Таким образом, радиальное перемещение u зависит только от r , перемещение v в направлении отсутствует, относительное удлинение по направлению оси z следует считать постоянным, т. е.

(2.19)

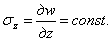
Для относительных удлинений в радиальном и тангенциальном направлениях возможно использовать соотношения (1.35,а), (1.35,б) т. е.

. (2.20)

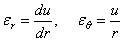
Очевидно в рассматриваемой задаче сохраняется уравнение равновесия из (1.32,б) т.е.

. (2.21)

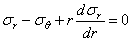
Использование (2.19) (2.20) в (2.16) и (2.18) с последующей подстановкой в (2.21) приводит к разрешающему уравнению следующего вида:

. (2.22)

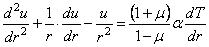
Решением (2.22) является выражение

. (2.23)

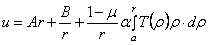
где 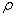— переменная интегрирования.

Далее, очевидно, подлежит подставить (2.23) в (2.17), (2.18), а для определения постоянных А , В и 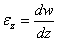использовать граничные уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то, следовательно:

Если труба не имеет осевой нагрузки, то

Приведем окончательные выражения для напряжений на внутренней и наружной поверх­ности трубы для случая, когда на этих поверхностях поддер­живаются постоянные температуры Т _а и Т _b и, следовательно, для такого установившегося потока распределение температур по толщине стенки выражается формулой:

. (2.24)

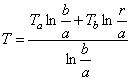
Тогда на внутренней и наружной поверхностях:

(2.25)

. (2.26)

2.2 Деформация толстостенного сферического сосуда

При решении некоторых задач, когда многие компоненты напряжений и деформаций отсутствуют, можно не прибегать к общим уравнениям теории упругости (в пе­ремещениях или в напряжениях), которые должны значительно упроститься, а все три необходимые стороны исследования (геометрическую, физическую и статическую) выполнить непосредственно применительно к рассматривае­мому частному случаю.

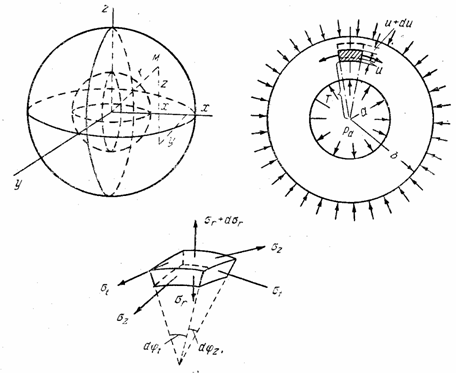
Представим себе шаровой сосуд, подвергающийся дей­ствию внутреннего и внешнего равномерных давлений. Пусть а и b обозначают соответственно внутренний и наружный радиусы шара (рис. 21), а р _a и р _b — внутреннее и наруж­ное давления газов.

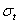
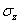
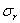
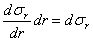
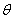
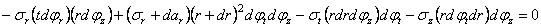
Начнем со статического обследования. Выре­жем для исследования бесконечно малый элемент двумя па­рами взаимно перпендикулярных меридиональных сечений и двумя концентрическими сферическими поверхностями. Дей­ствие отброшенных частей сосуда заменим тангенциальными ( , ) и радиальными ( ) напряжениями. Так как в рассма­триваемом случае напряжения зависят только от радиуса r , то напряжения по двум бесконечно близким друг к другу концентрическим поверхностям будут отличаться на величину и не будут зависеть от угла — другого параметра, определяющего местоположение рассматриваемого элемента. Проектируя все силы на нор­маль к элементу, имеем уравнение равновесия в виде:

.

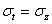
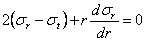
Имея в виду равенство и производя сокращения, получаем уравнение равновесия:

. (2.27)

Переходим к геометрическому обследованию. Из рассмотрения перемещений и формоизменения элемента заключаем, что относительное тангенциальное удлинение:

, (2.28)

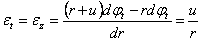
а относительное радиальное удлинение:

. (2.29)

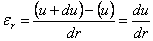
Выполним физическое обследование. Зави­симость напряжений от деформаций в данном случае имеет вид:

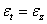
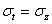
Напряжения через деформации выражаются (принимая во внимание равенство и ) так:

. (2.30)

Данные геометрического обследования используем для преобразования полученных физических зависимостей, т. е. подставляем (2.28) и (2.29) в (2.30). Имеем выражения для напряжений:

(2.31)

(2.32)

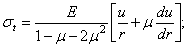
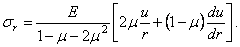
Выражения (2.31) и (3.32) подставляем в уравнение статики (12.27). Тогда после сокращений получаем выражение

, (2.33)

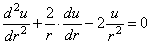
которое представляет собой уравнение, объединяющее в себе все три стороны исследования (геометрическую, физиче­скую и статическую).

Общий интеграл дифференциального уравнения (2.33) имеет вид

. (2.34)

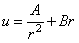
Дифференцируя (2.34), находим

. (2.35)

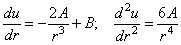
Подставляя (2.34) и (2.35) в (2.31) и (2.32), получаем вместо диф­ференциальной формы выражения для напряжений в алгебраи­ческой форме:

(2.36)

. (2.37)

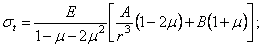
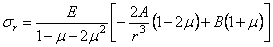
Постоянные интегрирования А и В определим из поверх­ностных условий:

.

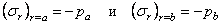
Тогда, в силу (2.37), имеем:

(2.38)

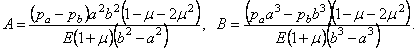
Подставляя (2.38) в (2.36) и (2.37), окончательно получим:

Для случая одного внутреннего давления р _a наибольшее растягивающее тангенциальное напряжение будет на внут­ренней поверхности сосуда (при r = a ):

а минимальное на наружной поверхности (при r = b ):

.

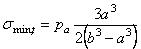
Приведенное здесь решение задачи теории упругости получено применением метода переме­щений.

2.3. Сосредоточенная сила, действующая на плоскость

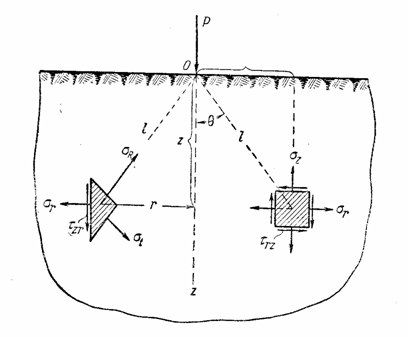
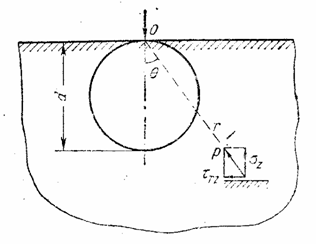
Пусть плоскость z = 0 является гранью полубесконечного сплошного тела пусть на эту плоскость действует сосредоточенная сила Р по оси z (рис. 22). В литературе эта задача име­нуется задачей Буссинеска .

Для радиального напряжения можно принять в качестве первой попытки

.

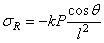
Переходя к цилиндрическим координатам, по формулам перехода должны получить

.

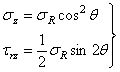
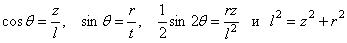
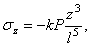
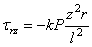
Заменяя , имеем:

(2.39)

. (2.40)

Для определения коэф­фициента k составим уравнение равновесия по какому-либо горизонтальному сечению z = a . Для элементарной площадки в виде бесконечно тонкого кольца шириной dr и радиуса r имеем элементарную внут­реннюю силу

.

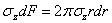
Со всех таких элементарных площадок, т. е. со всего сечения z = a , имеем сумму внутренних усилий

. (2.41)

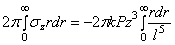
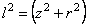
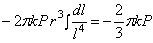
Так как , то, дифференцируя, имеем 2 ldl = 2 rdr . Таким образом, (2.41) перепишется:

.

Уравнение равновесия по сечению z = а (сумма проекций на ось z ) приводит к выражению

,

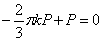
откуда .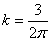

То, что выражения (2.39) и (2.40) дают точное решение задачи, можно доказать путем использования функции на­пряжений. Выполнение этой операции позволит определить нам также и другие компоненты напряжений ( , ).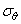

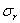
На основании (2.13, 2.14, 2.15)

.

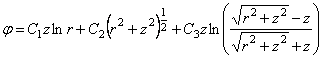
Окончательно формулы для напряжений примут вид:

. (2.42)

Для определения перемещений используем уравнения (2.2). Компо­нента смещения вдоль радиуса r

. (2.43)

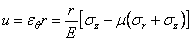
После подстановки в (2.43) выражений (2.42) и преобразо­ваний получаем

.

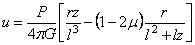
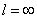
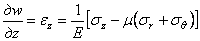
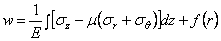
При , как и следует ожидать, и == 0. На основании этого

,

. (2.44)

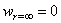
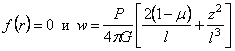
После подстановки в (2.44) выражений (2.42) и интегриро­вания, принимая также, что , получаем:

.

Для вертикальных перемещений точек на граничной плоскости z = 0 для так называемой “дневной поверхности” получим выражение:

. (2.45)

У начала координат, как это было и в плоской задаче, перемещения и напряжения становятся бесконечно боль­шими, и потому, необхо­димо представить, что у начала координат в области пла­стических деформаций материал вырезан полусферической поверхностью малого радиуса, а сосредоточенная сила Р заменена статически эквивалентными усилиями, распределен­ными по этой поверхности.

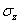
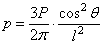
Полное напряжение в любой точке горизонтальной площадки (т.е. равнодействующая напряжений и на рис. 23)

.

Если, далее, очертить произволь­ным диаметром d сферу, касающуюся граничной плоскости в той же точ­ке O, то по всем горизонтальным площадкам, размещенным на поверх­ности этой сферы, полные напря­жения

.

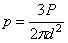
2.4 Частные случаи загрузки упругого полупространства

а) Равномерная загрузка по площади круга. Имея реше­ние для сосредоточенной силы, действующей на плоскую грань упругого полупростран­ства, найдем перемещения и напряжения, возникающие под действием распределенной нагрузки, если применим прин­цип сложения действия сил. Пусть нагрузка общим ве­сом Р равномерно распреде­лена на «дневной» поверхности полубесконечного тела по площади круга радиуса а . Ин­тенсивность нагрузки

.

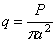
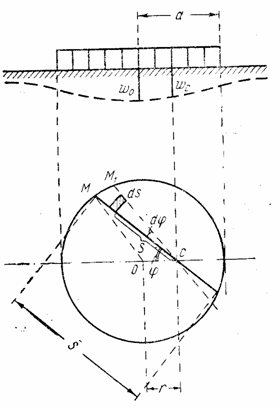
Составим выражения для перемещения точки С , нахо­дящейся на «дневной» поверх­ности, но в пределах загру­женного круга (рис. 24).

Проведем через точку С секущую МС, а в бесконечной близости другую – М₁С и рассмотрим влияние на «прогиб» точки С нагрузки, расположенной на элементарной площадке, заштрихованной на рис. 24. Эта площадка равна dF = sd 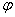ds , а нагрузка, на нее приходящаяся,

dP = qdF = qsd 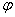ds . (2.46)

От такой нагрузки точка С должна опуститься согласно (2.45) на

и тогда получим

.

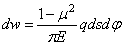
Полное перемещение точки С от всей нагрузки

.

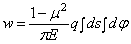
Из рис . 24 ясно, что взятый по всей длине секущей интеграл

. (2.47)

.

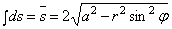
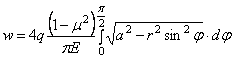
Для “прогиба” в центре круга, т. е. при r = 0, имеем:

.

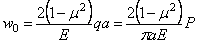
Таким образом, зная а , избавимся от бесконечности, полу­чаемой по формуле (2.45).

Для “прогиба” точек, лежащих на контуре загруженного круга, т. е. при r = а, получим:

.

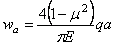
Отношение перемещений двух характерных точек

Перемещение точек, лежащих внутри загруженного круга, но не в центре его, могут быть вычислены на основании (2.48) с помощью таблиц аллиптических интегралов.

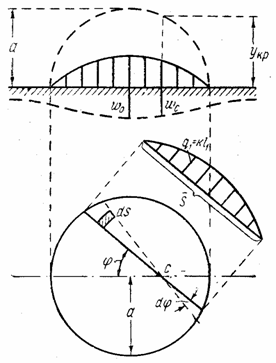
б) Загрузка на площади круга по “ полушару ”. Рас­смотрим случай, когда на площади круга радиуса а расположена нагрузка в ви­де шапки (рис. 25) таким образом, что в любой точ­ке загруженной территории интенсивность нагрузки

пропорциональна ординате полусферы, имеющей ра­диус а и основанием кото­рой служит упомянутая площадь круга. Иначе говоря, интенсив­ность нагрузки в любой точке согласно обозначе­ниям рис. 24 записывает­ся так:

;

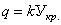
здесь У_{кр .} — ордината круга, имеющего радиус a , k — коэффициент нагрузки, т. е.

,

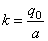
a q ₀ — наибольшая интенсивность нагрузки (т. е. в центре загруженной территории), причем q₀ может быть выражена через об­щий вес:

.

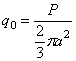
Для вычисления перемещения точки С , поступая анало­гично предыдущему примеру, имеем:

.

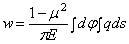
Выясним геометрический смысл последнего интеграла. Из рассмотрения рис. 25 следует, что

,

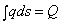
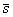
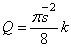
где Q — площадь эпюры нагрузки на длине . Но так как, рассекая сферу любой плоскостью, мы всегда в разрезе бу­дем получать круг, то и в данном случае, рассекая нагрузку, в общем изображаемую “ полушаром ”, мы всегда в разрезе должны получить “полукруг” (этой фи­гурой в разрезе будет полуэллипс ). Таким образом, можем записать

,

где k — коэффициент, позволяющий перейти от геометриче­ского полукруга к “полукругу” в кавычках. Итак,

или, на основании (2.47),

.

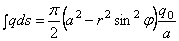
Теперь для полного перемещения точки С имеем:

.

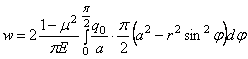
После интегрирования получаем:

, (2.49)

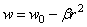
Если радиус изогнутой поверхности граничной плоскости будет велик по сравнению с радиусом загруженного круга, то выражение (2.49) можно практически считать уравнением некоторой сферической по­верхности.

в) Обратная задача. Очевидно, можно решать и обратные задачи, когда задано уравнение изогнутой «дневной» поверх­ности и требуется найти уравнение нагрузки, вызвавшей такую деформацию.

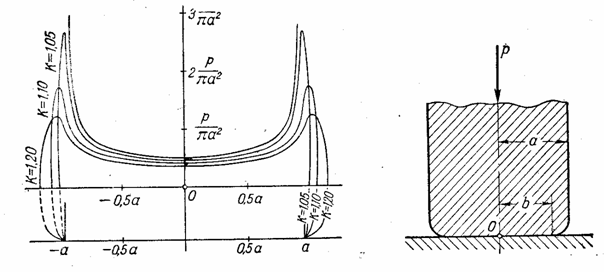
Возьмем, например, абсолютно жесткий штамп в виде круглого цилиндра, вдавливаемого в плоскую грань упругого полупространства. В этом случае перемещение w для всех точек будет по­стоянным по круглой подошве штампа; распределение дав­лений не будет постоянным и должно определяться в ре­зультате решения интегрального уравнения

Решение такого уравнения приводит к результату:

,

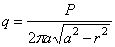
где Р — полная нагрузка на штамп, а — радиус штампа и r — радиус круга, на который действует давление q . Это рас­пределение неравномерно и наименьшее его значение в центре ( r = 0), где

,

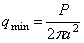
т.е. наименьшее давление равно половине среднего давле­ния по круговой площади подошвы штампа. На контуре этой площади ( r = a ) давление становится бесконечно большим.

Перемещение штампа выразится формулой

.

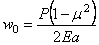
Если предположить, что края штам­па имеют некоторое закругление, как это показано на рис.26, то распределение напряжений у краев штампов может существенно измениться. Такая сложная контактная задача была поставлена И. Я. Штаерманом и при­вела к ответу, представленному графиком на рис. 26.

В частности, это решение свободно от бесконечно больших напряжений, не имеющих реального значения. На указанном графике .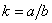

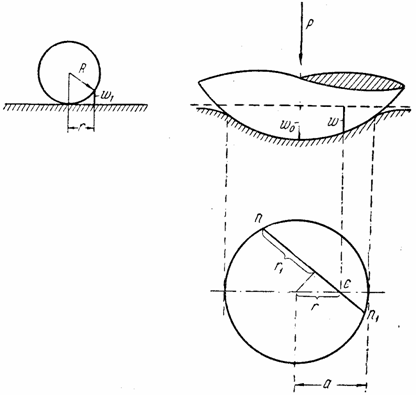
2.5 Вдавливание абсолютно жесткого шара в упругое полупространство

Представим, что на упругом полуространстве по­коится жесткий шар радиуса R (рис. 27). Если нет давле­ния на этот шар и исключить влияние собственного веса, то касание шара с граничной плоскостью полупространства бу­дет в точке. На расстоянии от точки касания, малом по сравнению с R , зазор между шаром и граничной плоскостью может быть, как известно, с достаточным приближением определен формулой:

.

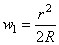
Если к шару будет приложена нагрузка, нормальная к первоначальной граничной плоскости и проходящая через дентр шара, то вследствие упругости полупространства гра­ничная плоскость изогнется и шар опустится, как это пока­зано на рис. 26 (справа).

Ввиду симметрии деформации относительно оси, совпа­дающей с направлением силы, площадка контакта шара с де­формированной граничной поверхностью упругого полупро­странства будет представлять в плане круг неко­торого радиуса а; закон распределения давления под шаром не известен, (подлежит определению). Очевидно, эпюра этого давления должна представлять фигуру, симметричную относительно оси, совпадающей с силой.

Проведя через точку С в плане бесконечно близкие секущие, вычислим нагрузку, приходящуюся на бес­конечно малую площадку dp , отстоящую на расстоянии s от точки С. Если напряжение смятия у этой площадки обозна­чим через q , то элементарная сила на площадке dF соответствует (2.45). Влияние этой силы на опускание точки Е определится, согласно (2.45), таким образом:

или, после подстановки (2.46),

.

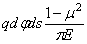
Влияние на прогиб рассматриваемой точки С всех элемен­тарных давлений со всей площади контакта шара и упругого полупространства оценится интегралом:

, (2.50)

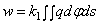
В выражении (2.50) неизвестными являются w и функция рас­пределения давления q . С другой стороны, из чисто геоме­трических соображений, поскольку шар не деформируется, следует (рис. 27) что

, (2.51)

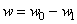
где w ₀ — опускание шара (и одновременно “прогиб” полу­пространства) в центре касания, a w ₁ — первоначальный зазор между шаром и граничной плоскостью. Тогда исследуемый прогиб

, (2.52)

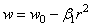
где введено обозначение:

.

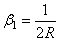
Уравнение (2.51) выражает условие, что «упругая» поверх­ность полупространства представляет под шаром часть по­верхности этого шара. Объединяя (2.50) и (2.52), имеем:

. (2.53)

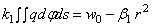
В выражении (2.53) неизвестная функция q входит под знак интеграла и, следовательно, (2.53) является интеграль­ным уравнением. Но именно такое же уравнение имелось и выше, где, наоборот, была известна нагруз­ка (он а была задана по “ полушару ”), а определялся характер изгиба граничной плоскости.

На основании сходства правых частей (2.53) и (2.49) заключаем, что эпюра распределения давления по площади контакта представляет “ полушар ”. Таким образом, если дав­ление в центре контакта обозначим через q ₀, то на расстоя­нии r от этого центра давление

,

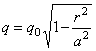
а при r = а (на контуре круга касания) обращается в нуль.

Все выражения предыдущего раздела целиком относятся и к данной задаче, т. е.

(2.54)

. (2.55)

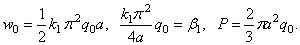
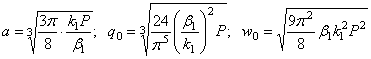
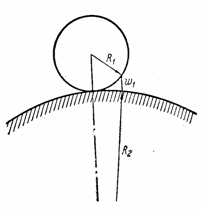
2.6. Задача об упругом смятии шаров

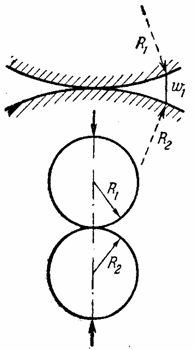
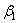
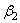
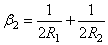
Представим, что абсолютно жесткий шар радиуса R ₁ по­коится на упругом теле сферической формы, имеющей очень большой радиус R ₂, и в дальнейшем подвергается действию силы Р (рис. 28). При вычислении глубины вдавливания радиуса площадки контакта и наибольшего напряжения смя­тия под указанным шаром мож­но использовать формулы (2.55), введя вместо прежнего новое значение , определяемое выражением:

.

Последнее выте­кает из зависимости, состав­ляемой для выбираемого перво­начального зазора w ₁ в случае касания двух сферических тел (рис. 28), и в данном случае имеем:

.

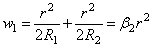
Таким образом, при вдавливании жесткого шара в “почти бесконечную” сферу, получаем

; (2.56)

; (2.57)

. (2.58)

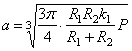
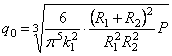
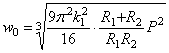
Полученные формулы могут употребляться лишь в случае, если радиус площадки смя­тия а будет весьма малым по сравнению с радиусом сферы R ₂, вследствие чего последнюю можно при небольших раз­мерах вдавливаемого шара считать “ полубесконечным ” те­лом, закон деформации которого был положен в основание вывода формул (2.55).

Если теперь представить случай двух упругих “почти бес­конечных” сфер, взаимно вдавливаемых силами Р (рис. 29), т. е. верхнюю сферу считать не абсолютно жесткой, а спо­собной деформироваться, то в этом случае можно

восполь­зоваться выводами предыдущей задачи, если ввести изменение в коэффициент, завися­щий от упругих свойств материалов, т. е. вместо k ₁ подставить

,

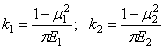
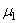
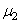
Е ₁ и — упругие характеристики матери­ала верхней сферы; E ₂ и то же для ниж­ней сферы.

Возможность такого простого перехо­да от формул (2.56), (2.57), (2.58) вытекает из тех соображений, что в данной задаче ввиду деформаций обеих сфер исходное уравнение деформации (2.53) должно быть записано в виде:

.

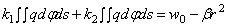
Последнее после введения обозначения (2.59), приводится к виду (2.53) с заменой k ₁ и k ₂.

Так как при сжатии упругих шаров радиус площадки смя­тия оказывается очень малым по сравнению с радиусами са­мих шаров, то рассмотренная сейчас задача о сжатии двух “почти бесконечных” сфер может быть практически исполь­зована и в задаче об упругом сжатии шаров (задача Герца). Итак, при сжатии шаров имеем:

; (2.60)

; (2.61)

. (2.62)

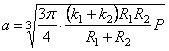
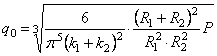
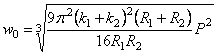
Зная закон распределения давления по поверхности контак­та, можно перейти к вычислению напряжений внутри шаров, используя для этой цели (2.42) и применяя принцип наложения.

Большой практический интерес представляет нахождение внутри сжимаемых шаров точек, имеющих большие касатель­ные напряжения. Исследование этого вопроса приводит к выводу, что точка, где касательное напряжение является наибольшим, лежит на оси z на глубине, равной примерно половине ра­диуса поверхности касания. Такую точку и следует рассматривать как самую опасную (в свете третьей теории прочности) для таких пластичных материалов, как сталь. Наибольшее касательное напряжение в этой точке (при = 0,3) составляет примерно 0,31 q ₀.

Из (2.60), (2.61), (2.62) следует, что радиус площадки смятия, взаимное вдавливание и напряжения смятия не находятся в линейной зависимости от силы Р. При увеличении силы Р напряжения и деформации шаров возрастают медленнее, чем возрастает сила.

Таким образом, в контактной задаче принятие в основу исследования линейной связи между компонентами напряже­ний и компонентами деформации в каждой точке упругого тела (обобщенный закон Гука) повлекло за собой нели­нейную зависимость между силой и перемещениями.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ ДЛЯ ПЛОСКОЙ ДЕФОРМАЦИИ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ ПРИ БИЛИНЕЙНОЙ АППРОКСИМАЦИИ ЗАМЫКАЮЩИХ УРАВНЕНИЙ Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Бакушев Сергей Васильевич

Рассматривается построение дифференциальных уравнений равновесия в перемещениях для плоского деформирования сплошных сред при билинейной аппроксимации замыкающих уравнений без учёта геометрической нелинейности в цилиндрической системе координат. Построение билинейных физических зависимостей основано на вычислении секущих модулей объёмного и сдвигового деформирования. При этом на первом участке диаграмм секущий модуль и объёмного и сдвигового деформирования постоянен, в то время как на втором участке диаграмм секущий модуль объёмного деформирования является функцией объёмной деформации, а секущий модуль сдвига является функцией интенсивности деформаций сдвига.

Похожие темы научных работ по физике , автор научной работы — Бакушев Сергей Васильевич

DIFFERENTIAL EQUATIONSOF BALANSED CONTINUUM FOR PLANAR DEFORMATION IN CYLINDRICAL COORDINATES AT BILINEAR APPROXIMATION OF CLOSSING EQUATIONS

Problems of the formulation of differential equations of equilibrium in terms of displacements for a plane strain of continuous media at bilinear approximation of closing equations are considered leaving out of account geometric nonlinearity in the cylindrical coordinate system. Based on the assumption that the curves of volumetric and shear strain are independent from each other, six main cases of physical dependencies are considered, which are the functions of the relative position of break points on the bilinear curves of the volumetric and shear strain. Obtaining of bilinear physical dependencies is based on the calculation of secant moduli of the volumetric and shear strain. On the first line of the curves, secant moduli are constant for both volumetric and shear strain, while on the second line, the secant modulus of the volumetric strain is a function of the volumetric strain, and the secant modulus of the shear strain is a function of the shear strain intensity. Putting the corresponding bilinear physical equations into differential equations of continuum equilibrium, which disregard geometrical nonlinearity, the resulting differential equations of equilibrium are obtained in terms of displacements for a one-dimensional plane strain of continuum in the cylindrical coordinate system. These equations can be used when determining stress-strain state of continuous media under one-dimensional plane strains with no regard for geometrical nonlinearity, and whose physical relations are approximated by bilinear functions.

Текст научной работы на тему «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ ДЛЯ ПЛОСКОЙ ДЕФОРМАЦИИ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ ПРИ БИЛИНЕЙНОЙ АППРОКСИМАЦИИ ЗАМЫКАЮЩИХ УРАВНЕНИЙ»

2021 Математика и механика № 69

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ ДЛЯ ПЛОСКОЙ ДЕФОРМАЦИИ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ ПРИ БИЛИНЕЙНОЙ АППРОКСИМАЦИИ ЗАМЫКАЮЩИХ УРАВНЕНИЙ

Рассматривается построение дифференциальных уравнений равновесия в перемещениях для плоского деформирования сплошных сред при билинейной аппроксимации замыкающих уравнений без учёта геометрической нелинейности в цилиндрической системе координат. Построение билинейных физических зависимостей основано на вычислении секущих модулей объёмного и сдвигового деформирования. При этом на первом участке диаграмм секущий модуль и объёмного и сдвигового деформирования постоянен, в то время как на втором участке диаграмм секущий модуль объёмного деформирования является функцией объёмной деформации, а секущий модуль сдвига является функцией интенсивности деформаций сдвига.

Ключевые слова: сплошная среда, плоская деформация, цилиндрические координаты, дифференциальные уравнения равновесия, билинейные замыкающие уравнения, геометрически линейная модель.

Вопросы построения замыкающих уравнений для сплошных нелинейно упругих сред, находящихся в условиях сложного напряжённого и деформированного состояния, позволяющие адекватно описать эволюцию их напряжённо-деформированного состояния, являются ключевыми [1, 2]. Фактические зависимости между объёмными деформациями и объёмным напряжениями, а также между сдвиговыми деформациями и сдвиговыми напряжениями являются, как правило, нелинейными и трудно поддающимися аналитическому описанию. Вместе с тем, даже в случае нелинейного аналитического описания замыкающих уравнений, решение конкретных задач методами теории упругости является чрезвычайно сложным процессом, обусловленным физической нелинейностью.

Для исключения эффектов физической нелинейности предлагается диаграммы объёмного ст = ст(е) и сдвигового T = T(Г) деформирования при сложном напряжённо-деформированном состоянии аппроксимировать билинейными функциями. При этом и на первом и на втором участках билинейных диаграмм объёмного и сдвигового деформирования можно будет использовать уравнения линейной (или геометрически нелинейной) теории упругости. Это с одной стороны. А с другой — разрешающие дифференциальные уравнения и системы дифференциальных уравнений, в силу линейных зависимостей между напряжениями и деформациями, будут иметь относительно простой вид.

Вопросам аппроксимации диаграмм работы материалов уделяется пристальное внимание. Так, в работе [3] рассмотрены практические вопросы аппроксимации опытных диаграмм работы неупругих материалов степенными и дробно-линейными функциями. Дана методика определения геометрического и физического смысла эмпирических коэффициентов, входящих в аппроксимирующие

формулы. В статье [4] показано, что результаты расчётов цилиндрической оболочки с сыпучим заполнителем при поперечном изгибе в геометрически и физически нелинейной постановке существенно отличаются от экспериментальных данных, если применяется билинейная аппроксимация диаграммы деформирования без учёта критических значений напряжений и деформаций. Отмечено, что точность решения во многом определяется величиной касательного модуля упрочнения материала. В работе [5], на основе положения о кинематической и статической определимости, описана методика определения диаграмм нелинейного деформирования разносопротивляющихся материалов при неоднородном напряжённо-деформированном состоянии, а также иллюстрируются основные приёмы (сплайн-аппроксимации) для достижения приемлемой точности результирующих функций. В работе [6] рассматриваются и анализируются физические законы связи напряжений и деформаций современной теории упругопластического деформирования, а также постулаты макроскопической определённости и изотропии начально-изотропных сплошных сред. Обсуждается вопрос о возможности применения постулата изотропии к оценке влияния параметров вида напряжённо-деформированного состояния, возникающего из-за деформационной анизотропии при изменении внутренней структуры материалов. Также обсуждается вопрос о правомерности представления симметричных тензоров второго ранга напряжений и деформаций в виде векторов координатного линейного евклидова шестимерного пространства. Предложен соответствующий принцип тождественности тензоров и векторов. В статье [7] для случая одноосного деформирования реологически сложных сред с учётом разносопротивляемости деформациям растяжения и сжатия приводится общая схема построения математических моделей, на базе которых строятся модели для пространственного напряжённо-деформированного состояния и обсуждаются вопросы идентификации входящих в них механических постоянных.

В настоящее время в связи с усложнением форм строительных конструкций, развитием авиастроения, кораблестроения, ракетостроения и так далее роль теории упругости как в линейной, так и в нелинейной постановке, резко изменилась. Теперь она составляет основу для построения практических методов расчёта деформируемых тел и систем тел разнообразной формы. При этом в современных прочностных и деформационных расчётах учитываются не только сложность формы тела и разнообразие воздействий (силовое, температурное и т.п.), но и специфика физических свойств материалов, из которых изготовлены тела.

Значительное внимание уделяется расчёту деформируемых тел с учётом геометрической и физической нелинейности. Так, в работе [8] на основе соотношений нелинейной теории упругости, в предположении простого активного нагру-жения, получено решение физически и геометрически нелинейной задачи о больших деформациях полой сферы, выполненной из несжимаемого материала. Полученные результаты свидетельствуют о существенном влиянии физической нелинейности материала сферы на функциональную зависимость перемещение — давление. Автором [9] разработана теория расчёта стержневых конструкций с учётом всех видов нелинейности. Изогнутая ось стержня аппроксимируется пространственной кривой. Получены системы разрешающих дифференциальных уравнений. В статье [10] приведен динамический критерий потери устойчивости прямоугольных в плане сферических оболочек при действии переменной во времени поперечной нагрузки с учётом двух типов нелинейности — геометрической и физической. Геометрическая нелинейность учитывается на основе соотношений

Т. Кармана. Физическая нелинейность описывается деформационной теорией пластичности А. А. Ильюшина. В статье [11] представлен вычислительный алгоритм, одновременно учитывающий физическую и геометрическую нелинейность деформирующейся среды, предназначенный для изучения статического упруго-пластического состояния вблизи транспортных подземных выработок произвольной формы. В основу алгоритма положена вариационная формулировка нелинейного конечно-элементного анализа. В работе [12] на основе гипотезы Эйлера -Бернулли построена теория нелинейной динамики неоднородной однослойной балки с учётом физической геометрической (в смысле Т. фон Кармана) нелинейности. Балка находится под действием знакопеременной нагрузки, распределённой равномерно по всей её поверхности. В статье [13] рассматриваются пологие оболочки на прямоугольном плане с учётом геометрической и физической нелинейности, а также неоднородности свойств материала по толщине оболочки. Авторами [14] рассмотрены процессы деформирования шарнирно закреплённых по торцам прямолинейных идеального и неидеального (неоднородного) стержней с параметром гибкости X = 867 при действии осевой сжимающей силы. В расчётной модели учтена геометрическая и физическая нелинейность, пластичность, изотропность, реальная диаграмма деформирования материала. Показано, что в идеальном стержне деформации обусловлены эффектом Пуассона, изгибных деформаций нет. Установлено, что для неидеального стержня существует критическая сила, при которой происходит потеря устойчивости стержня, связанная со значительными поперечными перемещениями (прогибами). Величина полученной критической силы согласуется с известным решением Эйлера.

Уравнения механики деформируемого твёрдого тела записываются, как правило, в соответствующей системе отсчёта — соответствующей системе координат. В зависимости от формы тела используются декартовы, полярные, цилиндрические, сферические 15 и другие координаты, например криволинейные подвижные лагранжевы [18], биполярные координаты [19]. Общие уравнения механики можно записать также и для общего случая произвольных криволинейных координат [1]. В данной работе используется наиболее часто применяемая в задачах, после декартовой, цилиндрическая система координат.

Цилиндрическая система координат используется при решении многих задач как линейной, так и нелинейной теории упругости. Так, в работе [20] выполнено исследование напряжённо-деформированного состояния пороупругого цилиндрического тела при радиальном равномерном сжатии, в результате чего построена математическая модель, описывающая неоднородное напряжённо-деформированное состояние цилиндрического тела для материалов с пористой структурой при упругой работе полностью сжатой матрицы. В [21] в цилиндрической системе координат рассматривается задача устойчивости кольцевых пластин с криволинейными структурами армирования в условиях плоского напряжённого состояния. Получен общий вид форм потери устойчивости, что позволило свести двумерную задачу к одномерной. Определены критические нагрузки для законов армирования по спирали Архимеда и логарифмической спирали. На основе метода малого параметра [22] построено аналитическое решение стохастической нелинейной краевой задачи установившейся ползучести для толстостенной трубы, находящейся под действием внутреннего давления в цилиндрических координатах. Приведено обобщение задачи расчёта толстостенной трубы, свойства материала которой описываются случайной функцией двух аргументов. В работе [23] в ци-

линдрической системе координат рассмотрено напряжённое состояние пространства, заполненного сыпучим материалом. Микроструктура сыпучего материала обусловливает возможность объёмной пластической деформации за счёт деформации сдвига. Это подтверждается ассоциированным законом течения к условию пластичности, предполагающего зависимость предельного касательного напряжённого состояния от давления, что, в свою очередь, допускает возможность замкнутого вида условия пластичности в пространстве главных напряжений. В той же системе координат методом конечных элементов рассматриваются состояния толстостенного цилиндра при двух видах нагружения в неоднородном температурном поле [24]. При этом исследуется влияние учёта связанности численного определения напряжённо-деформированного состояния и температурного поля на решение задачи нелинейной термоупругости. Статья [25] посвящена уп-ругопластическому кручению двухслойного слабоанизотропного стержня некругового поперечного сечения, представляющего собой двухсвязную область. Решение строится в предположении, что пластическая область целиком охватывает внешний контур поперечного сечения и существует упругопластическая граница, которая расположена между внутренним контуром и границей раздела слоёв. Задача решается в цилиндрической системе координат. В работе [26] так же в цилиндрической системе координат исследуется распространение нестационарных осесимметричных поверхностных возмущений в полупространстве, заполненном упругой однородной изотропной средой Коссера. Замкнутая система уравнений включает в себя уравнения относительно нетривиальных компонент потенциалов перемещения и угла поворота, а также соотношения, связывающие перемещения с потенциалами, и компонент тензоров напряжений и моментных напряжений с перемещениями и углом поворота. На граничной плоскости заданы нормальные перемещения. Показано, что учёт моментных напряжений приводит к качественным изменениям, а именно, наблюдается дополнительный волновой фронт. В статье [27] анализируются две анизотропные упругие модели, описывающие механическое поведение древесины: линейная ортотропная модель и цилиндрически ортотропная модель. Показано, что вторая модель является более сложной, но зато более адекватно описывает механические свойства древесины.

В статье [28] представлена разработка математической модели для описания механических свойств однослойных углеродных нанотрубок (ОСНТ). Связи углерод — углерод (С-С) между двумя соседними атомами смоделированы как балки Эйлера. Материальные константы балочного элемента — модуль Юнга и коэффициент Пуассона — определяются на атомном уровне. Расчёт выполнен в цилиндрических координатах. В данной работе строятся дифференциальные уравнения равновесия в перемещениях для случая плоского деформирования сплошной среды в цилиндрических координатах и = и (г, ф), V = V (г, ф), V = 0 при аппроксимации замыкающих уравнений произвольной формы билинейными функциями без учёта геометрической нелинейности. Дифференциальные уравнения равновесия в перемещениях для случая плоского деформирования сплошной среды в декартовых координатах при аппроксимации замыкающих уравнений произвольной формы билинейными функциями без учёта и с учётом геометрической нелинейности приведены в работах [29, 30], а для случая осесимметричного деформирования сплошной среды при аппроксимации замыкающих уравнений произвольной формы билинейными функциями с учётом и без учёта геометрической нелиней-

ности — в [31]. Дифференциальные уравнения равновесия в перемещениях для случая центрально-симметричного деформирования сплошной среды при аппроксимации замыкающих уравнений произвольной формы билинейными функциями с учётом и без учёта геометрической нелинейности разработаны в [32]. Вопросы аппроксимации диаграмм объёмного ст = ст(е) и сдвигового Т = Т(Г) деформирования при помощи билинейных функций, а также вопросы нахождения оптимального расположения точки излома на билинейном графике в [33].

Построение физических уравнений

В соответствии с рис. 1 и 2 секущие модули объёмного расширения (сжатия) К = К (е, Г) и сдвига О = О (е, Г) на первом прямолинейном участке диаграмм

ст = ст(е) и Т = Т (Г) будут определяться выражениями

Рис. 1. Диаграмма ст = ст(-) Fig. 1. Curve ст = ст(-)

Рис. 2. Диаграмма T = T (Г) Fig. 2. Curve T = T (Г)

На втором прямолинейном участке диаграмм ст = ст(е) и Т = Т(Г) секущий модуль объёмного расширения (сжатия) К = К (е, Г) и секущий модуль сдвига О = О (е, Г) будут определяться выражениями

Дифференциальные уравнения равновесия в цилиндрической системе координат

Если материальная точка P движется по кривой траектории, то положение точки может быть определено тремя цилиндрическими координатами: r, θ, z. Тогда положение точки, её скорость и ускорение могут быть записаны в единицах цилиндрических координат следующим образом:

Если разложить силу, действующую на материальную точку, вдоль единичных векторов цилиндрической системы координат, то уравнение движения можно записать в виде:

Для выполнения равенства, соответствующие компоненты u_r,u_θ,u_z левой части уравнения должны быть равны соответствующим компонентам в правой части уравнения. Таким образом, уравнение движения можно записать с помощью следующих скалярных компонентов:

Если движение происходит в двумерных координатах r-θ, то для описания движения необходимы только два первых уравнения.

Центростремительное и нормальное ускорение

Обычно задача заключается в определении компонентов результирующей силы: F_θ,F_r, F_z , которые приводят частицу в движение и задают ей определённое ускорение.

Сила P создаёт движение по траектории r = f(θ). Нормальная сила N всегда перпендикулярна касательной траектории в данной точке, в то время, как сила трения F всегда направлена вдоль касательной и против направления движения. Направления сил N и F могут быть определены относительно r-координаты используя угол θ, который определён между прямой-направлением радиуса и касательной в заданной точке.

Угол θ определяется смещением точки на расстояние ds вдоль траектории, радиальное перемещение составляет dr и перемещение в направлении касательной r dθ. Так как эти две составляющиевзаимно перпендикулярны, угол θ может быть определён из равенства:

Если угол θ положителен, то он измеряется от радиальной линии против направления хода часов или в положительном направлении угла θ. Если угол отрицательный, то он измеряется в обратном направлении (по часовой стрелке).

Например, кардиоида, описанная уравнением

когда θ=30°, tg = a(1+ cos 30°)/(-a sen 30°) = -3.73 2 , или θ = -75°, измеренный против направления хода часов, как представлено на изображении.

Алгоритм решения задач

Цилиндрические координаты удобно использовать для анализа систем, в которых траектории движения заданы относительно радиальной линии, или могут быть удобным образом выражены в цилиндрических координатах. Определив координаты точки, уравнения движения могут быть применены для выражения силы в виде компонентов ускорения.

1. Установить инерциальную систему координат r, θ, z и изобразить диаграмму свободного тела
2. Положить ускорения a_r, a_θ, a_z направлены вдоль положительного направления осей r, θ, z, если направления неизвестны
3. Определить все неизвестные величины в задачи

Применить уравнения движения