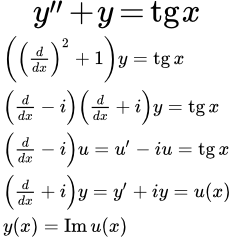Дифференциальные уравнения с комплексными числами

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Дифференциальные уравнения
• Высшая математика.
• Комплексные числа

Комплексные числа

Действия над комплексными числами.

Комплексные числа — числа вида $x+iy,$ где $x,y\in \mathbb$ а
$\,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $\mathbb.$

Действия над комплексными числами.

Сложение комплексных чисел:

Умножение двух комплексных чисел:

Умножение комплексного числа на действительное:

$$\lambda(x+iy)=\lambda x+i\lambda y.$$

Деление комплексных чисел:

Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$

Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$

Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$

Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.

Примеры:

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.421. $(2+3i)(3-i).$

Решение:

Ответ: $9+7i.$

1.424. $(2i-i^2)^2+(1-3i)^3.$

Решение.

Ответ: $24+22i.$

Решение.

Ответ: $\frac<1><2>-\frac<3><2>i.$

Решение.

Ответ: $\frac<14><5>i.$

Найти действительные решения следующего уравнения:

1. 430. $(1+i)x+(-2+5i)y=-4+17i.$

Решение.

Ответ: $x=2; y=3.$

Домашнее задание.

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.422. $(1+2i)^2.$

Ответ: $-3+4i.$

1.423. $(1-i)^3-(1+i)^3.$

1.427. $\left(\frac<1-i><1+i>\right)^3.$

Найти действительные решения следующего уравнения:

1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$

Решить следующие системы линейных уравнений:

1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$

$(4+2i)z_1-(2+3i)z_2=7.$

1.433. $(2+i)z_1+(2-i)z_2=6;$

$(3+2i)z_1+(3-2i)z_2=8.$

Геометрическая интерпретация комплексных чисел.

Множество действительных чисел можно рассматривать как подмножество комплексных чисел, у которых $Im z = 0.$

Можно также изображать комплексное число в виде радиус-вектора $\$ и определять его, задавая его длину $r$ и угол $\varphi$ между осью $Ox$ и вектором.

Длина этого вектора называется модулем комплексного числа $$|z|=r=\sqrt\geq 0,$$ а угол $\varphi$ называется аргументом комплексного числа и обозначается $Arg z.$ Аргумент определяется с точностью до слагаемого $2\pi k\,\,\,\,\, (k=0, \pm 1, \pm 2, \pm 3, . )$ и для положительных значений отсчитывается от оси $Ox$ до вектора против часовой стрелки, а для отрицательных значений – по часовой стрелке.

Значение аргумента, который принадлежит интервалу $(-\pi, \pi],$ называется главным значением аргумента и определяется $arg z.$ Главное значение аргументу числа $x+iy$ можно вычислять по формуле $\varphi= arg z=arctg\left(\frac\right)+k\pi,$ где $k=0,$ если $z$ находится в первой или четвертой четвертях, $k=1,$ если $z$ находится во второй четверти, $k=-1,$ если $z$ находится в третей четверти. Если $x=Rez=0,$ то $\varphi=\pi/2,$ когда $y=Imz>0$ и $\varphi=-\pi/2,$ когда $y=Imz плоскость называется комплексной плоскостью C (рисунок 1), ось $Ox$ называется действительной осью, а ось $Oy$ – мнимой осью. Таким образом, действительному числу $z=x+0i=x$ отвечает точка на действительной оси, а мнимому числу $z=0+iy=y -$ точка на мнимой оси.

Формулы Эйлера и Муавра. Корень n-й степени с комплексного числа.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Формулы Эйлера:

Формула Муавра:

Если $z=re^, $ то $$z^n=r^ne^,$$ или, в тригонометричской форме:

$$z^n=r^n(\cos n\varphi+i\sin n\varphi).$$

Пусть $a=re^, \,\, a\neq 0,-$ фиксированное комплексное число. Тогда уравнение $z^n=a,\,\,\, n\in N,$ имеет в точности $n$ различных решений $z_0, z_1, . z_$ причем эти решения даются формулой $$z_k=\sqrt[n]e^+\frac<2\pi>k\right)>=\sqrt[n]\left(\cos\frac<\varphi+2\pi k>+i\sin\frac<\varphi+2\pi k>\right),$$ $$k=0, 1, . , n-1.$$ (здесь $\sqrt r$ действительное положительное число) Числа $z_k, \,\, k=0, 1, . n-1,$ называются корнями $n-$й степени из комплексного числа $a$ и обозначаются символом $\sqrt[n].$

Примеры:

1.483. Доказать формулу Эйлера $\cos\varphi=\frac+e^<-i\varphi>><2>.$

Решение.

Известно, что $e^=\cos<\varphi>+i\sin\varphi.$ Соответственно, $e^<-i\varphi>=\cos<(-\varphi)>+i\sin(-\varphi)=\cos\varphi-i\sin\varphi.$

Отсюда находим $e^+e^<-i\varphi>=\cos\varphi+i\sin\varphi+\cos\varphi-i\sin\varphi=2\cos\varphi.$

Cледовательно, $\cos\varphi=\frac+e^<-i\varphi>><2>.$ Что и требовалось доказать.

Используя формулу Муавра, вычислить следующие выражения:

1.485. $(1+i)^<10>.$

Решение.

Запишем число $z=1+i$ в показательной форме:

Поскольку число $z$ находится в первой четверти, то

Таким образом, мы можем записать число $z=1+i$ в показательной форме: $z=\sqrt 2 e^<4>>.$

Теперь, используя формулу Муавра можно найти $z^<10>:$

Ответ: $(1+i)^<10>=32i.$

1.491. Используя формулу Муавра, выразить через $\cos\varphi$ и $\sin\varphi$ функцию$\cos 3\varphi.$

Решение.

$$+\left.\cos^3(-\varphi)-3i\cos^2(-\varphi)\sin(-\varphi)+3i^2\cos(-\varphi)\sin^2(-\varphi)-i^3\sin^3(-\varphi)\right)=$$ $$=\frac<1><2>\left(\cos^3<\varphi>+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)\right.-i\sin^3\varphi+$$ $$+\left.\cos^3\varphi+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)-i\sin^3\varphi\right)=$$ $$=\cos^3\varphi+3i\sin\varphi-3i\sin^3\varphi-3\cos\varphi+3\cos^3\varphi-i\sin^3\varphi=$$ $$=4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$$

Ответ: $4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$

1.495. Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степени из единицы.

Решение.

Запишем число 1 в показательной форме:

$1=1e^<0i>.$ То есть $r=1, \varphi=0.$

Далее, пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Вычисляем корень третьей степени из единицы:

Вычисляем корень четвертой степени из единицы:

Ответ: Корни второй степени: $z_0=1;\,\, z_1 =-1.$ Корни третьей сепени: $z_0=1;\,\, z_1=-\frac<1><2>+i\frac<\sqrt 3><2>;\,\, z_2=-\frac<1><2>-i\frac<\sqrt 3><2>.$ Корни четвертой степени: $z_0=1;\,\, z_1=i;\,\, z_2=-1;\,\, z_3=-i.$

Найти все значения корней:

Решение.

Запишем число $z=-1+i\sqrt 3$ в показательной форме:

Поскольку число $z$ находится во второй четверти, то

Таким образом, мы можем записать число $z=-1+i\sqrt 3$ в показательной форме: $z=2 e^<3>>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Ответ: $\pm\frac<\sqrt 2><2>(1+i\sqrt 3)$

1.501. $\sqrt [5]<-1-i>.$

Решение.

Запишем число $z=-1-i 3$ в показательной форме:

Поскольку число $z$ находится в третьей четверти, то

Таким образом, мы можем записать число $z=-1-i$ в показательной форме: $z=\sqrt 2 e^<4>>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

1.483. Доказать формулу Эйлера $\sin\varphi=\frac-e^<-i\varphi>><2i>.$

Используя формулу Муавра, вычислить следующие выражения:

Используя формулу Муавра, выразить через $\cos\varphi$ и $\sin\varphi$ следующие функции:

Выражения, уравнения и системы уравнений
с комплексными числами

Сегодня на занятии мы отработаем типовые действия с комплексными числами, а также освоим технику решения выражений, уравнений и систем уравнений, которые эти числа содержат. Данный практикум является продолжением урока Комплексные числа для чайников, и поэтому если вы неважно ориентируетесь в теме, то, пожалуйста, пройдите по указанной выше ссылке. Ну а более подготовленным читателям предлагаю сразу же разогреться:

Упростить выражение , если . Представить результат в тригонометрической форме и изобразить его на комплексной плоскости.

Решение: итак, требуется подставить в «страшную» дробь, провести упрощения, и перевести полученное комплексное число в тригонометрическую форму. Плюс чертёж.

Как лучше оформить решение? С «навороченным» алгебраическим выражением выгоднее разбираться поэтапно. Во-первых, меньше рассеивается внимание, и, во-вторых, если таки задание не зачтут, то будет намного проще отыскать ошибку.

1) Сначала упростим числитель. Подставим в него значение , раскроем скобки и поправим причёску:

…Да, такой вот Квазимодо от комплексных чисел получился…

Напоминаю, что в ходе преобразований используются совершенно бесхитростные вещи – правило умножения многочленов и уже ставшее банальным равенство . Главное, быть внимательным и не запутаться в знаках.

2) Теперь на очереди знаменатель. Если , то:

Заметьте, в какой непривычной интерпретации использована формула квадрата суммы . Как вариант, здесь можно выполнить перестановку под формулу . Результаты, естественно, совпадут.

3) И, наконец, всё выражение. Если , то:

Чтобы избавиться от дроби, умножим числитель и знаменатель на сопряженное знаменателю выражение. При этом в целях применения формулы разности квадратов следует предварительно (и уже обязательно!) поставить отрицательную действительную часть на 2-е место:

А сейчас ключевое правило:

НИ В КОЕМ СЛУЧАЕ НЕ ТОРОПИМСЯ! Лучше перестраховаться и прописать лишний шаг.
В выражениях, уравнениях и системах с комплексными числами самонадеянные устные вычисления чреваты, как никогда!

На завершающем шаге произошло хорошее сокращение и это просто отличный признак.

Примечание: строго говоря, здесь произошло деление комплексного числа на комплексное число 50 (вспоминаем, что ). Об этом нюансе я умалчивал до сих пор и о нём мы ещё поговорим чуть позже.

Обозначим наше достижение буквой

Представим полученный результат в тригонометрической форме. Вообще говоря, здесь можно обойтись без чертежа, но коль скоро, требуется – несколько рациональнее выполнить его прямо сейчас:

Вычислим модуль комплексного числа:

Если выполнять чертёж в масштабе 1 ед. = 1 см (2 тетрадные клетки), то полученное значение легко проверить с помощью обычной линейки.

Найдём аргумент. Так как число расположено во 2-й координатной четверти , то:

Угол элементарно проверяется транспортиром. Вот в чём состоит несомненный плюс чертежа.

Таким образом: – искомое число в тригонометрической форме.

Выполним проверку:
, в чём и требовалось убедиться.

Незнакомые значения синуса и косинуса удобно находить по тригонометрической таблице.

Ответ:

Аналогичный пример для самостоятельного решения:

Упростить выражение , где . Изобразить полученное число на комплексной плоскости и записать его в показательной форме.

Постарайтесь не пропускать учебные примеры. Кажутся-то они, может быть, и простыми, но без тренировки «сесть в лужу» не просто легко, а очень легко. Поэтому «набиваем руку».

Краткое решение и ответ в конце урока.

Нередко задача допускает не единственный путь решения:

Решение: прежде всего, обратим внимание на оригинальное условие – одно число представлено в алгебраической, а другое – в тригонометрической форме, да ещё и с градусами. Давайте сразу перепишем его в более привычном виде: .

В какой форме проводить вычисления? Выражение , очевидно, предполагает первоочередное умножение и дальнейшее возведение в 10-ю степень по формуле Муавра, которая сформулирована для тригонометрической формы комплексного числа. Таким образом, представляется более логичным преобразовать первое число. Найдём его модуль и аргумент:

Используем правило умножения комплексных чисел в тригонометрической форме:
если , то

Далее применяем формулу Муавра , которая является следствием указанного выше правила:

Делая дробь правильной, приходим к выводу, что можно «скрутить» 4 оборота ( рад.):

Второй способ решения состоит в том, чтобы перевести 2-е число в алгебраическую форму , выполнить умножение в алгебраической форме, перевести результат в тригонометрическую форму и воспользоваться формулой Муавра.

Как видите, одно «лишнее» действие. Желающие могут довести решение до конца и убедиться, что результаты совпадают.

В условии ничего не сказано о форме итогового комплексного числа, поэтому:

Ответ:

Но «для красоты» либо по требованию результат нетрудно представить и в алгебраической форме:

Здесь нужно вспомнить действия со степенями, хотя одного полезного правила в методичке нет, вот оно: .

И ещё одно важное замечание: пример можно решить в двух стилях. Первый вариант – работать с двумя числами и мириться с дробями. Второй вариант – представить каждое число в виде частного двух чисел: и избавиться от четырёхэтажности. С формальной точки зрения без разницы, как решать, но содержательное отличие есть! Пожалуйста, хорошо осмыслите:
– это комплексное число;
– это частное двух комплексных чисел ( и ), однако в зависимости от контекста можно сказать и так: число , представленное в виде частного двух комплексных чисел.

Краткое решение и ответ в конце урока.

Выражения – хорошо, а уравнения – лучше:

Уравнения с комплексными коэффициентами

Чем они отличаются от «обычных» уравнений? Коэффициентами =)

В свете вышеприведённого замечания начнём с этого примера:

И незамедлительная преамбула по «горячим следам»: изначально правая часть уравнения позиционируется, как частное двух комплексных чисел ( и 13), и поэтому будет нехорошим тоном переписать условие с числом (хотя это и не повлечёт ошибки). Более явственно данное различие, кстати, просматривается в дроби – если, условно говоря, , то это значение в первую очередь понимается как «полноценный» комплексный корень уравнения, а не как делитель числа , и тем более – не как часть числа !

Решение, в принципе, тоже можно оформить пошагово, но в данном случае овчинка выделки не стОит. Первоначальная задача состоит в том, чтобы упростить всё, что не содержит неизвестной «зет», в результате чего уравнение сведётся к виду :

Уверенно упрощаем среднюю дробь:

Результат переносим в правую часть и находим разность:

Примечание: и вновь обращаю ваше внимание на содержательный момент – здесь мы не вычли из числа число, а подвели дроби к общему знаменателю! Следует отметить, что уже в ХОДЕ решения не возбраняется работать и с числами: , правда, в рассматриваемом примере такой стиль скорее вреден, чем полезен =)

По правилу пропорции выражаем «зет»:

Теперь можно снова разделить и умножить на сопряжённое выражение, но подозрительно похожие числа числителя и знаменателя подсказывают следующий ход:

Ответ:

В целях проверки подставим полученное значение в левую часть исходного уравнения и проведём упрощения:

– получена правая часть исходного уравнения, таким образом, корень найден верно.

…Сейчас-сейчас… подберу для вас что-нибудь поинтереснее… держите:

Данное уравнение сводится к виду , а значит, является линейным. Намёк, думаю, понятен – дерзайте!

Конечно же… как можно без него прожить:

Квадратное уравнение с комплексными коэффициентами

На уроке Комплексные числа для чайников мы узнали, что квадратное уравнение с действительными коэффициентами может иметь сопряжённые комплексные корни, после чего возникает закономерный вопрос: а почему, собственно, сами коэффициенты не могут быть комплексными? Сформулирую общий случай:

Квадратное уравнение с произвольными комплексными коэффициентами (1 или 2 из которых либо все три могут быть, в частности, и действительными) имеет два и только два комплексных корня (возможно один из которых либо оба действительны). При этом корни (как действительные, так и с ненулевой мнимой частью) могут совпадать (быть кратными).

Квадратное уравнение с комплексными коэффициентами решается по такой же схеме, что и «школьное» уравнение, с некоторыми отличиями в технике вычислений:

Найти корни квадратного уравнения

Решение: на первом месте расположена мнимая единица, и, в принципе, от неё можно избавиться (умножая обе части на ), однако, в этом нет особой надобности.

Для удобства выпишем коэффициенты:

Не теряем «минус» у свободного члена! …Может быть не всем понятно – перепишу уравнение в стандартном виде :

А вот и главное препятствие:

Применение общей формулы извлечения корня (см. последний параграф статьи Комплексные числа для чайников) осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами). Но существует и другой, «алгебраический» путь! Корень будем искать в виде:

Возведём обе части в квадрат:

Два комплексных числа равны, если равны их действительные и их мнимые части. Таким образом, получаем следующую систему:

Систему проще решить подбором (более основательный путь – выразить из 2-го уравнения – подставить в 1-е, получить и решить биквадратное уравнение). Предполагая, что автор задачи не изверг, выдвигаем гипотезу, что и – целые числа. Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары:

Очевидно, что 1-му уравнению системы удовлетворяют две последние пары, таким образом:

Не помешает промежуточная проверка:

что и требовалось проверить.

В качестве «рабочего» корня можно выбрать любое значение. Понятно, что лучше взять версию без «минусов»:

Находим корни, не забывая, кстати, что :

Ответ:

Проверим, удовлетворяют ли найденные корни уравнению :

Таким образом, решение найдено правильно.

По мотивам только что разобранной задачи:

Найти корни уравнения

Следует отметить, что квадратный корень из чисто комплексного числа прекрасно извлекается и с помощью общей формулы , где , поэтому в образце приведены оба способа. Второе полезное замечание касается того, что предварительное извлечение корня из константы ничуть не упрощает решение.

А теперь можно расслабиться – в этом примере вы отделаетесь лёгким испугом 🙂

Решить уравнение и выполнить проверку

Решения и ответы в конце урока.

Заключительный параграф статьи посвящён

системе уравнений с комплексными числами

Расслабились и… не напрягаемся =) Рассмотрим простейший случай – систему двух линейных уравнений с двумя неизвестными:

Решить систему уравнений. Ответ представить в алгебраической и показательной формах, изобразить корни на чертеже.

Решение: уже само условие подсказывает, что система имеет единственное решение, то есть, нам нужно найти два числа , которые удовлетворяют каждому уравнению системы.

Систему реально решить «детским» способом (выразить одну переменную через другую), однако гораздо удобнее использовать формулы Крамера. Вычислим главный определитель системы:

, значит, система имеет единственное решение.

Повторюсь, что лучше не торопиться и прописывать шаги максимально подробно:

Домножаем числитель и знаменатель на мнимую единицу и получаем 1-й корень:

Перед тем, как продолжать дальше, целесообразно проверить решение. Подставим найденные значения в левую часть каждого уравнения системы:

Получены соответствующие правые части, ч.т.п.

Представим корни в показательной форме. Для этого нужно найти их модули и аргументы:

1) – арктангенс «двойки» вычисляется «плохо», поэтому так и оставляем:

Ответ:

Решить систему уравнений

Найти произведение корней и представить его в тригонометрической форме.

Краткое решение совсем близко.

И в заключение ответим на экзистенциальный вопрос: для чего нужны комплексные числа? Комплексные числа нужны для расширения сознания выполнения заданий других разделов высшей математики, кроме того, они используются во вполне материальных инженерно-технических расчетах на практике.

На этом курс Опытного пользователя комплексных чисел завершён – сертификат вам на стену и новых достижений!

Решения и ответы:

Пример 2: Решение: если , то:

Умножим числитель и знаменатель на сопряжённое знаменателю выражение:

Изобразим полученное число на чертеже:

Представим ответ в показательной форме. Найдем модуль и аргумент данного числа:

Поскольку число расположено в 3-й четверти, то:

Таким образом:
Ответ:

Пример 4: Решение:

Пример 6: Решение:

Умножим обе части уравнения на :

Ответ:

Пример 8: Решение:
Первый способ: корни уравнения ищем в виде:

Возведём обе части в квадрат:

Комплексные числа равны, если равны их действительные и их мнимые части:

Из 1-го уравнения следует, что:
1) , но это не удовлетворяет 2-му уравнению (равенство выполняется только в том случае, если и одного знака);
2) – подставим во 2-е уравнение:

Таким образом: либо
Ответ:

Второй способ: используем формулу . В данном случае :

Найдём модуль и аргумент комплексного числа:
;
очевидно, что .
Таким образом:

Ответ:

Пример 9: Решение: . Вычислим дискриминант:

Таким образом:

Ответ:

Проверка: подставим в исходное уравнение :

верное равенство;

верное равенство.
Что и требовалось проверить.

Пример 11: Решение: систему решим методом Крамера:

Таким образом, система имеет единственное решение.
Найдём произведение корней:

Представим результат в тригонометрической форме:

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения

Метод понижения порядка линейного неоднородного дифференциального уравнения с комплексными корнями характеристического уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) .
Мы полагаем, что коэффициенты этого уравнения являются действительными числами. Здесь мы рассматриваем случай, когда характеристическое уравнение
(2)
имеет комплексные корни.

Для решения уравнения (1), применим метод понижения порядка. Поскольку коэффициенты характеристического уравнения (2) являются действительными числами, то его комплексные корни являются попарно комплексно сопряженными. Пусть – два комплексно сопряженные корня: . Запишем исходное уравнение (1) в следующем виде:
(3) ,
где – оператор дифференцирования.

Обозначим:
.
Тогда уравнение (3) принимает следующий вид:
.
Сделаем подстановку:
(4) .
Получаем уравнение первого порядка с комплексным коэффициентом :
.
Или
(5) .
Решение этого уравнения имеет следующий вид (см. страницу метод понижения порядка ):
,
где – комплексная постоянная.

Далее замечаем, что поскольку исходное уравнение (1) имеет действительные коэффициенты, то переменная u и ее производная u′ должны быть действительными. Выразим комплексный корень через действительную и мнимую части:
.
Подставим в (4):
.
Извлекая мнимую часть, получаем:
.
Отсюда
.

Таким образом, в случае с комплексными корнями, один этап решения приводит к понижению порядка на две единицы.

Пример решения дифференциального уравнения

Решить уравнение
(П1) .

Перепишем уравнение в следующем виде:
.
Вводим обозначение :
.

Характеристическое уравнение

имеет комплексные корни: . Тогда
.

Переписываем исходное уравнение:
;
.
Делаем подстановку:
;
(П2) .
Тогда уравнение принимает вид:
;
(П3) .

Это линейное неоднородное дифференциальное уравнение первого порядка. Ищем решение с помощью интегрирующего множителя. Умножим на и выполняем преобразования:
;
;
(П4) ,
где – комплексная постоянная; – действительные постоянные.

Вычисляем интеграл в (П4) с помощью подстановки .

.

Выразим арктангенс через логарифм, используя уравнение: .
;
.
Отсюда
(П5) .

Теперь в правой части (П6) нам нужно отделить вещественную и мнимую части. Мнимая часть уравнения (П6) и даст искомое решение y .

Для преобразования логарифма, используем формулу: . Далее замечаем, что . Тогда при имеем:
.
При :
.
Оба случая можно записать одной формулой:
,
где при нужно взять верхний знак ′+′; при – нижний знак ′–′.

Подставим в (П6) и выполним преобразования:
;
.
Переобозначим постоянную :
(П7) .

Теперь преобразуем экспоненту с помощью формулы Эйлера: , и выразим комплексную постоянную через действительную и мнимую части: . Подставляем в (П7):
.
Выполняем преобразования:

.
Тогда

.
Отделяем мнимую часть:

.

Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 26-08-2020