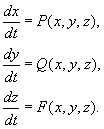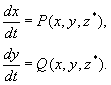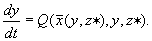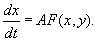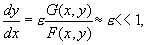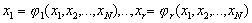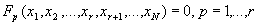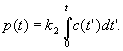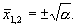Дифференциальные уравнения с малым параметром и релаксационные колебания

Дифференциальные уравнения с малым параметром и релаксационные колебания

Авторы: А.С. Холодов, А.И. Лобанов, А.В. Евдокимов

• Линейные многошаговые схемы (методы типа Адамса).

• Алгоритм и аппроксимация

Используя, как и в разделе 1.3 , метод неопределенных коэффициентов и записывая линейную комбинацию вектор-функций v и правых частей f в некоторой последовательности равноотстоящих точек t n , t n +1 , . t n + k ( t = t n + k t – t n + k = const ), для линейных многошаговых методов получим следующее разностное выражение:

(43)

Из-за однородности (43), коэффициент при искомом значении v n + k можно выбрать единичным:

Неопределенные коэффициенты a k , b k ( k =0 . K ) из разложения (43) в ряд Тейлора в точке t n + k (или t n ) связаны условиями аппроксимации (на решениях (18) ):

, (45)

(обеспечивают первый порядок аппроксимации),

(46)

(обеспечивает второй порядок аппроксимации вместе с (45)),

(47)

(обеспечивает n –ый порядок аппроксимации на решениях (18) вместе с предшествующими условиями).

Схемы первого порядка аппроксимации малоинтересны, поэтому в дальнейшем будем рассматривать схемы второго или более высокого порядка точности. Если с учетом нормировки (44) и условий аппроксимации второго порядка точности (45), (46) исключить, например,

,

,

.

то оставшиеся свободными коэффициенты (если позволяет выбранное K> 2), можно принять за линейное пространство размерности 2( K –1), например, с евклидовой метрикой, и каждой точке в этом пространстве будет соответствовать некоторая разностная схема второго порядка точности, а условия более высокого порядка аппроксимации ((47) при n =3 и т.д.) после исключения в них a k , a k –1 , b k , b k –1 , являясь относительно оставшихся свободными коэффициентов a k , b k ( k= 0,…, K –2) линейными уравнениями

,

образуют в этом пространстве соответствующую гиперплоскость схем третьего порядка аппроксимации. На пересечении двух таких гиперплоскостей ((47) при n =3 и n =4) будут расположены схемы с четвертым порядком аппроксимации и т.д., пока мы не исчерпаем все возможности для выбранного K , т.е. пока не найдем единственную схему с наиболее высоким (для данного K ) порядком аппроксимации (одну из точек в этом пространстве).

В частности, при K = 2 имеем:

где a 0 и b 0 произвольны для схем второго порядка аппроксимации.

Условие третьего порядка аппроксимации дает прямую в плоскости 0 , b 0 > с уравнением

а единственной схемой четвертого порядка аппроксимации будет точка на этой прямой с координатами:

• Устойчивость

Как уже отмечалось, одной аппроксимации недостаточно для сходимости решений (43) к решениям исходной дифференциальной задачи даже в линейном случае (7). Необходимо еще обеспечить устойчивость разностных схем (43). Для одного линейного уравнения, полагая f= l v из (43) получим

. (50)

Устойчивость разностных схем (50) будем исследовать на специальных решениях вида v n =q n . Тогда для определения q имеем многочлен устойчивости степени K и уравнение

,

корни которого q j , j =1 , 2 . K (действительные или комплексные, в зависимости от s , a k , b k ) должны удовлетворять условиям устойчивости

• Сингулярно — возмущенная система — модель двухлампового генератора Фрюгауфа

Система более высокой размерности, имеющая решение в виде релаксационного цикла, приведена в [4] (см. также [8]). Она имеет вид:

Здесь ? > 0 — константа порядка единицы, функция

T k = 20, ? = 10 –3 , 10 –6 .

• Простейшая модель гликолиза

Простейшая модель гликолиза описывается уравнениями следующего вида [8]:

предложенными Дж. Хиггинсом. В системе ? = 10, ? = 100, 200, 400, 1000. Начальные условия для системы: y 1 (0) = 1, y 2 (0) = 0,001, T k = 50. Решение этой системы — релаксационные автоколебания (жесткий предельный цикл).

• Модель химических реакций Робертсона

Один из первых и самых популярных примеров «жесткой» системы ОДУ принадлежит Робертсону (1966) и имеет вид, типичный для моделей химической кинетики — в правой части системы стоят полиномы второй степени от концентраций (сравните с орегонатором).

Система Робертсона имеет вид [1]:

Начальные условия для системы таковы: y 1 (0) = 1, y 2 (0) = 0, y 3 (0) = 0. Рассматриваются следующие величины отрезка интегрирования: T k = 40 (в работе Робертсона рассматривался именно такой отрезок интегрирования), T k = 100, 1000, …, 10 11 . О свойствах задачи см. в [1].

• Модель дифференциации растительной ткани

Данный пример из [1] — типичный случай биохимической модели «умеренной» размерности (современные модели, например, фотосинтеза включают сотни уравнений подобного типа). Хотя данная модель является умеренно жесткой, тем не менее, ее лучше решать с помощью методов, предназначенных для решения ЖС ОДУ.

Начальные значения всех переменных системы равны 0, кроме y 1 (0) = 1 и y 8 (0) = 0.0057. Длина отрезка интегрирования T k = 421,8122.

• Задача E5

Еще одна модель химической реакции из [1], получившая свое название Е5 в более ранних публикациях.

Начальные условия: y 1 (0) = 1,76•10 –3 , а все остальные переменные равны 0. Значения коэффициентов модели следующие: A = 7,89•10 –10 , B = 1,1•10 7 , C = 1,13•10 3 , M = 10 6 . Первоначально задача ставилась на отрезке T k = 1000, но впоследствии было обнаружено, что она обладает нетривиальными свойствами вплоть до времени T k = 10 13 (подробнее см. [1]).

Обратите особое внимание, что в процессе расчетов приходится иметь дело с очень малыми концентрациями реагентов (малы значения y 2 , y 3 и y 4 ). Как «подправить» постановку задачи E5?

• Уравнение Релея

Уравнение Релея во многом похоже на уравнение Ван-дер-Поля [8]. Рассматривается задача вида

.

Решить задачу, записав уравнение Релея в виде системы ОДУ. Начальные условия: x (0) = 0, ? = 1000, T k = 1000.

• Экогенетическая модель

Рассмотрим пример системы уравнений, которая описывает изменения численности популяций двух видов и эволюцию некого генетического признака ? . Система ОДУ имеет вид:

Параметры задачи таковы: ? ? 0,01, 0 ? x 0 ? 3, 0 ? y 0 ? 15, ? 0 = 0, T k = 1500. Наличие малого параметра в третьем уравнении системы показывает, что генетический признак меняется медленнее, чем численность популяций. Решение системы — релаксационные колебания.

Задача описана в статье [9].

• Экогенетическая модель

Еще один пример жесткой системы описан в статье [9]. Более интересный случай — численность двух популяций зависит от взаимодействия между ними и двух медленно меняющихся генетических признаков.

Параметры задачи таковы: ? ? 0,01, 0 ? x 0 ? 40, 0 ? y 0 ? 40, ? 10 = 0, ? 20 = 10, T k = 2000.

Рассмотреть также модификацию предыдущей системы [9]:

Параметры задачи: ? ? 0,01, 0 ? x 0 ? 40, 0 ? y 0 ? 40, ? 10 = 0, ? 20 = 10, T k = 2000.

Литература

• Э. Хайрер, Г. Ваннер . Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально – алгебраические задачи. — М.: Мир, 1999. — 685 с.

• Э. Хайрер, С. Нерсетт, Г. Ваннер . Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. — М.: Мир, 1990. — 512 с.

• Колебания и бегущие волны в химических системах: Пер. с англ. / Под ред. Р. Филда, М. Бургер . — М. : Мир, 1988. — 720 с.

• Е. Ф. Мищенко, Н. Х. Розов . Дифференциальные уравнения с малым параметром и релаксационные колебания. — М.: Наука, 1975. — 248 с.

• Е. Ф. Мищенко, Ю. С. Колесов, А. Ю. Колесов, Н. Х. Розов . Периодические движения и бифуркационные процессы в сингулярно-возмущенных системах — М.: Наука. Физматлит, 1995. — 336 с.

• Г. Г. Малинецкий Хаос. Структуры. Вычислительный эксперимент. — М.: Наука, 1998. (или Эдиториал УРСС, 2000.)

• Д. Каханер, К. Моулер, С. Нэш. Численные методы и программное обеспечение. — М.: Мир, 1998. — 575 с.

• П. С. Ланда . Нелинейные колебания и волны. — М.: Наука. Физматлит, 1997. — 496 с.

• А. С Кондрашов, А. И. Хибник. Экогенетические модели как быстро-медленные системы. / В кн.: Исследования по математической биологии. – Пущино, 1996. — с. 88–123.

• Ракитский Ю.В.,Устинов С.М., Черноруцкий И.Г. Численные методы решения жестких систем. – М.: Наука, 1979 (п.п. 1-4).

• Холл Дж., Уатт Дж. (ред.). Современные численные методы решения обыкновенных дифференциальных уравнений. – М.: Мир, 1979 (п.п.1-4).

• Калиткин Н.Н. Численные методы. – М.: Наука, 19?? (п.12).

Введение. Релаксационные колебания являются одним из видов автоколебаний, т

Релаксационные колебания являются одним из видов автоколебаний, т. е. незатухающих колебаний, возникающих в так называемых автоколебательных системах под влиянием процессов, происходящих внутри системы. Для поддержания автоколебаний не требуется никаких внешних периодических воздействий. В этом отношении автоколебания радикально отличаются от вынужденных колебаний, которые также могут быть незатухающими, но для своего существования требуют периодических внешних воздействий (в механике – внешних сил, в электричестве – приложенных извне напряжений).

В состав автоколебательных систем входит источник энергии (в случае механических колебаний – сжатая пружина, поднятый груз и т. д., в случае электрических – батарея гальванических элементов или иной источник тока). Этот источник периодически включается самой системой и вводит в нее определенную энергию, компенсирующую потери на трение или выделение тепла Джоуля-Ленца, что и делает колебания незатухающими.

Так как автоколебания устанавливаются под влиянием процессов, происходящих внутри автоколебательной системы, то они возникают самопроизвольно (самовозбуждение) под действием случайных малых воздействий, выводящих систему из равновесия (флуктуации). Возникшие малые колебания самопроизвольно нарастают, и в конце концов в системе образуются установившиеся колебания, свойства которых (период, интенсивность, форма) определяются параметрами системы и не зависят от начальных условий.

Кроме релаксационных (резко несинусоидальных) колебаний может наблюдаться и другой вид автоколебаний – почти гармонические колебания, которые происходят, например, в часах или в ламповом генераторе. В каждую подобную систему входят два элемента, способные запасать энергию (в случае лампового генератора это катушка индуктивности и конденсатор), в то время, как в релаксационной автоколебательной системе имеется лишь один накопитель энергии (например, конденсатор).

В процессе генерирования почти гармонических электрических колебаний происходит периодическое превращение энергии электрического поля, связанного с электроёмкостью, в энергию магнитного поля, связанного с индуктивностью, и обратно. Потери энергии во время колебаний периодически восполняются источником энергии, входящим в автоколебательную систему. Релаксационный же автоколебательный процесс заключается в периодической аккумуляции энергии накопителем и периодическом расходовании накопленной энергии путем превращения ее в другие виды.

Наиболее простой схемой для генерирования электрических релаксационных колебаний является схема, основными элементами которой служат конденсатор и неоновая лампа.

Работа схемы существенно зависит от свойств неоновой лампы, которая представляет собой газоразрядный прибор, конструктивно выполненный в виде двух параллельных или коаксиальных электродов, помещенных в баллон, наполненный неоном при небольшом давлении. Характерной особенностью такой неоновой лампы является то, что она начинает проводить ток («зажигается») только при определенном напряжении – «напряжении зажигания» U_З,которое зависит от расстояния между электродами, их формы и от давления газа, и гаснет при существенно меньшем напряжении – «напряжении гашения» U_Г.

Вольтамперная характеристика неоновой лампы изображена на рис. 1. Из этого рисунка видно, что при малых напряжениях на электродах ток в лампе равен 0. При достижении напряжения зажигания U_З в лампе возникает разряд, и ток скачком достигает конечной величины – тока зажигания I_З. При дальнейшем увеличении напряжения ток в лампе продолжает расти почти линейно. Если затем уменьшать напряжение, то спад тока идет по другой кривой, близкой к первой, и лишь при достижении напряжения гашения U_Г, которое меньше U_З, ток скачком падает от значения I_Г до нуля – лампа гаснет.

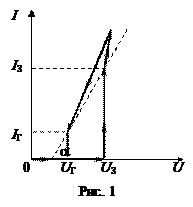Для упрощения расчетов можно взять идеализированную характеристику неоновой лампы, которая представляет собой отрезок прямой линии, проходящей через точки I_Г, U_Г и I_З, U_З и пересекающей ось напряжений U под углом a. По идеализированной характеристике можно численно определить внутреннее сопротивление лампы:

R_i = ctga = (U_З — U_Г)/(I_З — I_Г) .

Рассмотренные свойства неоновой лампы позволяют объяснить механизм возникновения релаксационных колебаний в схеме, приведенной на рис. 2.

Пусть в начальный момент времени (t =0) напряжение на конденсаторе С равно нулю и неоновая лампа (Ne) не горит (ее внутреннее сопротивлениеR_i = ¥).

После подключения источника тока конденсатор С заряжается и напряжение на нем возрастает по кривой ОА (рис. 3а), стремясь стать равным напряжению, снимаемому с потенциометра U_П. Но раньше, чем оно достигнет этого значения, лампа зажжется. Это произойдет при напряжении U = U_З. При этом внутреннее сопротивление R_i неоновой лампы скачком становится конечным, численно равным ctga (см. рис. 1). После этого начинается разряд конденсатора, причем напряжение на обкладках конденсатора падает по экспоненте АВ, стремясь асимптотически сравняться с некоторым предельным значением U_ПР. Однако при напряжении U_Г, несколько большим U_ПР, лампа гаснет, то есть внутреннее сопротивление скачком принимает значение R_i = ¥, и конденсатор снова начинает заряжаться, причем напряжение на нем растет по кривой ВС. Когда напряжение на обкладках конденсатора станет равным U_З, лампа снова зажжётся. Дальше процесс повторяется периодически.

Как видно из рис. 3а, зависимость напряжения от времени представляет собой непрерывную кривую, в то время как соответствующая кривая тока носит разрывный характер. Колебания тока, представленные на рис. 3б, и называются разрывными или релаксационными.

Следует заметить, что релаксационные колебания в схеме, представленной на рис. 2, могут возникнуть, если параметры неоновой лампы U_З и U_Г лежат внутри интервала асимптотических значений U_ПР и U_П, то есть при выполнении следующего условия:

Период релаксационных колебаний Т складывается из времени зарядки конденсатора t_З и времени его разрядки t_Р:

Время зарядки конденсатора в процессе колебаний может быть определено как:

где t₂ – время зарядки конденсатора до напряжения U_З, t₁ – время зарядки конденсатора до напряжения U_Г (см. рис. 3а).

Значения t₂ и t₁ определяются из формулы (2):

U_З = U_П(1 — ); U_Г = U_П(1 — ).

t₂ = —RC×ln ; t₁ = —RC×ln .

t₃ = t₂ — t₁ = RC×ln . (3)

Время разрядки определим по аналогичной формуле (считая, что U_ПР = 0)

t_Р = R_iC×ln . (4)

Если выбирать сопротивление R достаточно большим (R >> R_i), то t_Р будет много меньше t_З, и период релаксационных колебаний можно считать равным

T » t₃ = RC×ln . (5)

Из (5) следует, что период колебаний пропорционален постоянной времени RC.

Таким образом, измеряя U_П, U_З и U_Г и зная электрические параметры схемы, можно определить период релаксационных колебаний.

Релаксационные электрические колебания нашли многочисленные практические применения в радиотехнике и измерительной технике. Они используются для измерения неизвестных сопротивлений и емкостей, для измерения частоты в широких пределах, используются для создания генераторов пилообразных колебаний, применяемых в электронных осциллографах и т.д.

ЛЕКЦИЯ 6

ПРОБЛЕМА БЫСТРЫХ И МЕДЛЕННЫХ ПЕРЕМЕННЫХ. ТЕОРЕМА ТИХОНОВА. ТИПЫ БИФУРКАЦИЙ. КАТАСТРОФЫ

Метод квазистационарных концентраций. Теорема Тихонова. Уравнение Михаэлиса Ментен. Бифуркации динамических систем. Типы бифуркаций. Бифуркационные диаграммы и фазопараметрические портреты. Катастрофы.

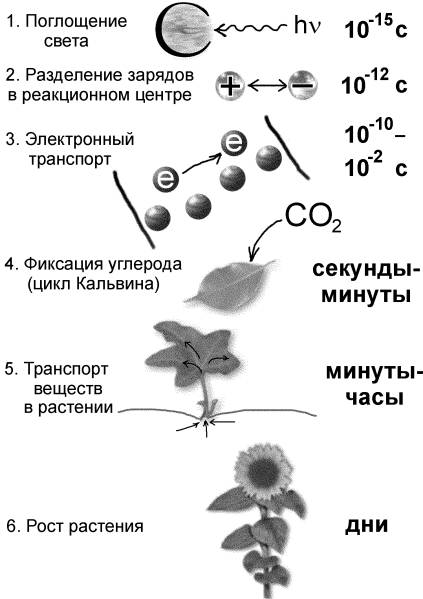
Биологические системы включают большое число процессов с разными характерными временами, причем иерархия этих времен такова, что они различаются на много порядков. Примером такой иерархической системы является процесс фотосинтеза, который обеспечивает существование жизни на Земле.

Рис. 6.1. Иерархия фотосинтетических процессов

Благодаря фотосинтезу образуется органическое вещество из углекислого газа и воды с использованием энергии солнечного света и неорганических веществ из почвы и воды. Фотосинтез также служит источником земного кислорода, необходимого для дыхания всех аэробных организмов. Иерархия времен процессов, вовлеченных в процесс фотосинтеза растений, представлена на рис. 6.1.

Степень подробности моделирования изучаемых явлений зависит от цели моделирования. Однако в любом случае задача моделирования заключается в том, чтобы построить модель явления, содержащую возможно меньшее число переменных и произвольных параметров, и в то же время правильно отражающую свойства явления.

Учет временной иерархии процессов позволяет сократить число дифференциальных уравнений. «Совсем медленные» переменные не меняются на временах рассматриваемых процессов, и их можно считать постоянными параметрами. Для «быстрых» переменных можно вместо дифференциальных уравнений записать алгебраические уравнения для их стационарных значений, поскольку «быстрые» переменные достигают своих стационарных значений практически мгновенно по сравнению с «медленными».

Средние, быстрые и медленные времена.

Пусть имеется три группы переменных с различными характерными временами:

Переменные изменяются с разными характерными временами, причем

.

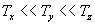
Пусть мы наблюдаем за переменной y, характерное время изменения которой ‑ T_y . Тогда за время T_y «совсем медленная» переменная z практически не будет изменяться, и ее можно считать постоянным параметром, обозначим его z * .

Система дифференциальных уравнений с учетом этого обстоятельства будет содержать два уравнения и может быть записана в виде:

Отметим, что z * не является истинно стационарным значением, «медленная» переменная z будет продолжать меняться и «вести» за собой более быстрые переменные x и y . В этом смысле медленная переменная является ведущей, или «параметром порядка».

Рассмотрим теперь уравнение для x. Эта «быстрая» переменная изменяется значительно быстрее, чем y, и за время T_y успеет достичь своего стационарного значения. Значит, для переменной x дифференциальное уравнение можно заменить алгебраическим:

P(x, y, z * ) =0

.

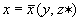
Таким образом, благодаря учету иерархии времен, исходную систему из трех дифференциальных уравнений удается свести к одному дифференциальному уравнению для переменной y :

В химической кинетике метод такой редукции системы был впервые предложен Боденштейном и носит название метода квазистационарных концентраций (КСК).

Обычно он применяется для систем химических реакций, промежуточные продукты которых являются частицами с высокой реакционной способностью. К ним относятся каталитические процессы, свободно радикальные и цепные реакции.

В процессах с участием активных промежуточных частиц разность скоростей образования v_о и расхода v_р этих частиц мала по сравнению с этими скоростями. Режим называется квазистационарным , а отвечающие ему концентрации активных промежуточных веществ — квазистационарными концентрациями.

Дифференциальные уравнения для промежуточных соединений:

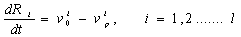
можно заменить алгебраическими:

.

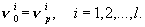
Из l алгебраических уравнений можно выразить l квазистационарных концентраций промежуточных химических соединений. По мере расходования исходных веществ, квазистационарные концентрации промежуточных соединений будут меняться, но если время установления квазистационарного режима мало, он не будет нарушаться в течение всего процесса.

Конечно, такое рассмотрение не правомерно для начальных стадий процесса, когда R_i меняются от нуля до своих квазистационарных значений. Этот период носит название периода индукции.

Разработке метода КСК и оценке длительности периода индукции посвящены работы Бенсона, Семенова, Франк-Каменецкого.

Аналогичная ситуация имеет место в биохимических ферментативных процессах, где процессы образования и распада фермент-субстратного комплекса происходят значительно быстрее, чем процессы расходования субстрата и образования продукта.

Теорема Тихонова

Математически строгое обоснование применения метода квазистационарных концентраций (редукции системы в соответствии с иерархией времен) и формулировка условий его применимости дана в работе А.Н. Тихонова (1952).

Рассмотрим простейший случай двух дифференциальных уравнений

. (6.1)

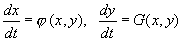
Пусть y ‑ медленная, а x ‑ быстрая переменная. Это означает, что отношение приращений D y и D x за короткий промежуток времени D t много меньше единицы:

Скорость изменения x значительно превосходит скорость изменения y, поэтому правую часть первого уравнения можно записать в виде:

Первое уравнение системы можно представить в виде:

Разделив левую и правую часть уравнения на А и обозначив e = 1 /A, получим полную систему уравнений, тождественную исходной:

(6.2)

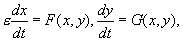
где e малый параметр.

Если характер решения не изменится при устремлении малого параметра e к нулю (условия этого обстоятельства и составляют содержание теоремы Тихонова), можно устремить e к нулю и получить для «быстрой» переменной x вместо дифференциального уравнения — алгебраическое.

(6.3)

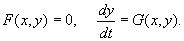
В отличие от полной такая система называется вырожденной . Фазовый портрет такой системы представлен на рис. 6.2.

Фазовые траектории в любой точке фазовой плоскости за исключением e — окрестности кривой F(x,y)= 0 имеют наклон, определяемый уравнением:

т.е. расположены почти горизонтально. Это области быстрых движений, при которых вдоль фазовой траектории y=const, а x быстро меняется. Достигнув по одной из таких горизонталей e — окрестности кривой F(x,y)= 0 , изображающая точка потом будет двигаться по этой кривой.

Рис. 6.2

Фазовый портрет системы 6.3.

Скорость движения по горизонтальным участкам траектории dx/dt » 1 / e =A, т.е. очень велика по сравнению со скоростью движения в окрестности кривой F(x,y)= 0. Поэтому общее время достижения некоего состояния на кривой F(x,y) определяется лишь характером движения вдоль этой кривой, т.е. зависит лишь от начальных значений медленной переменной y и не зависит от начальных значений быстрой переменной x .

Отметим, что квазистационарные значения быстрых переменных являются функциями не окончательных стационарных значений медленных переменных, а лишь их мгновенных значений. В этом смысле говорят о том, что быстрая переменная «подчинена» медленной.

Теорема Тихонова устанавливает условия редукции системы дифференциальных уравнений с малым параметром (условия замены дифференциальных уравнений для быстрых переменных ‑ алгебраическими).

Запишем систему N уравнений, часть из которых содержит малый параметр e перед производной.

, (6.4)

. (6.5)

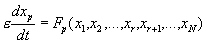
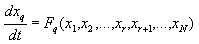
Назовем систему (6.4) присоединенной , а систему (6.5) ‑ вырожденной .

Решение полной системы (6.4 — 6.5) стремится к решению вырожденной системы (6.5) при e ® 0 , если выполняются следующие условия:

a) решение полной и присоединенной системы единственно, а правые части непрерывны;

б) решение

представляет собой изолированный корень алгебраической системы

(в окрестности этого корня нет других корней);

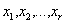
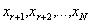
в) решение — устойчивая изолированная особая точка присоединенной системы (6.4) при всех значениях ;

г) начальные условия 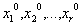попадают в область влияния устойчивой особой точки присоединенной системы.

Число начальных условий вырожденной системы меньше, чем полной: начальные значения быстрых переменных не используются в вырожденной системе. Согласно теореме Тихонова, если выполняется условие в), результат не зависит от начальных условий для переменных присоединенной системы.

Таким образом, необходимым условием редукции является наличие малого параметра в уравнениях (6.4).

Представляет интерес система двух дифференциальных уравнений вида (6.2), в которой особая точка расположена на неустойчивой ветви кривой F ( x,y ) = 0 . Такая система совершает релаксационные колебательные движения. Вопрос о релаксационных колебаниях мы обсудим в лекции 8.

Теорема Тихонова явно или неявно применяется при исследовании практически любых моделей биологических систем, в этом мы убедимся в дальнейшем (лекции 7-12).

Фермент-субстратная реакция Михаэлиса-Ментен

Классическим примером является модель базовой ферментативной реакции, предложенная Михаэлисом и Ментен в 1913 г.

Схема реакции может быть представлена в виде:

E + S ES, ES P + E (6.6)

Схема означает, что субстрат S соединяется с ферментом E в комплекс ES , в котором происходит химическое превращение, и который затем распадается на фермент E и продукт P . По закону действующих масс, скорость реакции пропорциональна произведению концентраций. Обозначив концентрации реагентов малыми буквами:

получим систему уравнений:

(6.7)

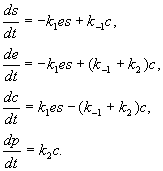
В системе (6.7.) учтены следующие процессы:

· Субстрат S расходуется, образуя комплекс ES (бимолекулярная реакция), и его концентрация увеличивается при распаде комплекса;

· Фермент E расходуется на образование комплекса ES , его концентрация увеличивается при распаде комплекса.

· Комплекс ES образуется из фермента E и субстрата S (бимолекулярная реакция) и распадается на субстрат S и фермент E.

· Продукт P образуется при распаде комплекса.

Для полной математической формулировки задачи Коши необходимо задать начальные условия:

Уравнения (6.7) не являются независимыми. Кроме того, последнее уравнение отделяется от первых трех. Если система первых трех уравнений решена, концентрация продукта может быть рассчитана по формуле:

В соответствии со схемой реакций (6.6 — 6.7) общее количество фермента, свободного и связанного в комплекс, сохраняется:

Это условие позволяет одно из дифференциальных уравнений системы (6.7) заменить алгебраическим, и модель сводится к двум дифференциальным уравнениям:

(6.9)

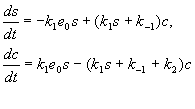
Введем безразмерные переменные и параметры:

(6.10)

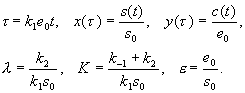
Запишем уравнения (6.9) в безразмерном виде:

(6.11)

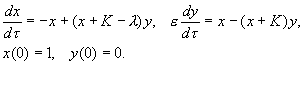
Поскольку реакция превращения фермент-субстратного комплекса необратима, уже из схемы реакций (6.6) ясно, что с течением времени весь субстрат будет превращен в продукт, и в стационарном состоянии концентрации и субстрата и комплекса станут равны нулю: x = 0 , y = 0 .

Систему (6.7) нельзя решить аналитически. Проанализируем качественно, как ведут себя x ( t ) и y ( t ) .

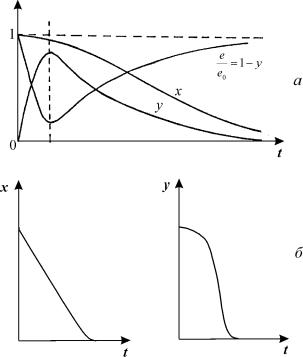
Вблизи t = 0 dx / d t 0. Это означает, что x уменьшается от x = 1 . В то же время dy / dt > 0, y растет от y = 0 до величины y = x /( x + K ), при которой правая часть уравнения для dy / dt обращается в нуль. После этого величина y будет уменьшаться до нуля. Таким образом, концентрация фермент-субстратного комплекса y проходит через максимум. В это время величина x (концентрация субстрата) монотонно уменьшается. Относительная концентрация свободного фермента e / e ₀ сначала убывает а затем снова возрастает до величины e / e ₀ = 1, поскольку с течением времени субстрат исчерпывается, и все меньшая доля фермента оказывается связанной. Кинетические кривые изображены на рис. 6.2.

Рис. 6.2. Кинетика изменения безразмерных переменных в уравнении Михаэлиса-Ментен. а – с учетом области переходных процессов на малых временах (полная система 6.11). б – без учета области переходных процессов (редуцированная система 6.12)

Предположим, что концентрация субстрата значительно превышает концентрацию фермента: s ₀ >> e ₀ . Тогда из соотношений (6.10) следует, что e 1 . Если условия Теоремы Тихонова выполняются (для уравнений Михаэлиса-Ментен это можно показать), мы имеем право заменить второе из уравнений (6.11) алгебраическим и найти «квазистационарную концентрацию» фермент-субстратного комплекса:

. (6.12)

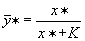
По терминологии Тихонова, мы получим вырожденную систему:

(6.13)

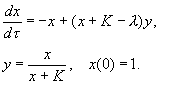
Подставив выражение для y в дифференциальное уравнение для x , получим:

.

Рис. 6.3. Закон Михаэлиса-Ментен. Зависимость скорости реакции как функция начальной концентрации субстрата S . m ₀ – максимальная скорость, K_m — константа Михаэлиса.

В размерном виде это – классическая формула Михаэлиса — Ментен для кинетики изменения субстрата в ферментативной реакции:

. (6.14)

Таким образом, формула (6.14) верно отражает изменение концентрации субстрата, но ничего не может сказать об изменении концентраций свободного фермента и фермент-субстратного комплекса, которые на малых временах ведут себя немонотонно (см. рис. 6.2).

Величина K_m называется константой Михаэлиса и имеет размерность концентрации. При s K_m скорость пропорциональна концентрации: — m ₀ s / K_m . Она соответствует концентрации субстрата, при которой скорость 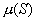равна половине максимальной. Максимальная скорость ферментативной реакции m ₀ = k ₂ e ₀ и зависит линейно от константы скорости стадии распада ферментативного комплекса, которую называют лимитирующей стадией.

В эксперименте для оценки параметров ферментативной реакции используют кривую зависимости скорости реакции от концентрации субстрата (рис.6.3, формула 6.14)

В ферментативных реакциях возможны гораздо более сложные типы динамического поведения: два или несколько устойчивых стационарных состояния, автоколебания, квазистохастические режимы. Эти типы поведения мы рассмотрим в следующих лекциях. Они связаны с изменением характера фазового портрета системы, который содержит не одну стационарную точку, как это мы видели в лекциях 4, 5, а носить более сложный характер. Для того, чтобы понять, как возможны такие усложнения в поведении системы, рассмотрим понятие бифуркации .

Бифуркации динамических систем.

Мы рассматриваем динамические модели биологических процессов, то есть считаем, что система может быть описана системой дифференциальных уравнений:

(6.15)

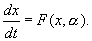
Здесь x – вектор переменных, a — вектор параметров.

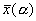
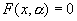
Пусть – стационарное решение – особая точка системы, координаты которой представляют собой решение системы алгебраических уравнений:

. (6.16)

Зафиксируем некоторое a = a *, и рассмотрим фазовые портреты системы при данном значении параметра, а также при a > a * и a a *.

Фазовые портреты топологически эквивалентны, если существует невырожденное непрерывное преобразование координат, которое переводит все элементы одного фазового портрета в элементы другого. Для того чтобы представить себе такое преобразование на поверхности, представим себе, что поверхность резиновая, ее можно сжимать и изгибать, но нельзя перекручивать. При таких преобразованиях все начальные точки будут однозначно переходить в точки деформированной «резиновой» поверхности, незамкнутые кривые будут переходить в незамкнутые, замкнутые – в замкнутые, связность множеств не будет нарушаться. Такое преобразование происходит с фазовыми кривыми при невырожденном непрерывном преобразовании координат.

Недаром говорят, что топология – это «резиновая геометрия »

Если фазовые портреты при значениях a > a * и a a * топологически не эквивалентны, это означает, что при 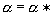происходит качественная перестройка системы. Тогда говорят, что a * — бифуркационное значение параметра.

Простейший пример бифуркационного значения параметра – нулевое значение собственной константы скорости роста в уравнении экспоненциального роста (2.7):

.

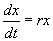
При r > 0 стационарное значение ` x = 0 – неустойчиво, при r 0 – устойчиво. r *= 0 — бифуркационное значение параметра. Напомним, что биологический смысл величины r – разница коэффициентов рождаемости и смертности. Если рождаемость преобладает – популяция растет, если преобладает смертность – вымирает. Переход от выживания к вымиранию – качественная перестройка системы.

С понятием бифуркации мы также столкнулись в лекции 3, когда рассматривали смену режимов в дискретном уравнении Ферхюльста при увеличении параметра роста. Там режим монотонного роста сменялся режимом двухточечного цикла, следующее бифуркационное значение параметра приводило к четырехточечному циклу, каждая дальнейшая бифуркация вела к удвоению предельного цикла, и, наконец, наступал хаос.

Бифуркационную диаграмму для системы двух линейных автономных уравнений мы рассматривали в лекции 4. На рис. 4.11 представлена бифуркационная диаграмма для системы двух линейных автономных уравнений. На ней мы видим бифуркационные границы двух типов – линии – оси координат 0 x ¥ , — ¥ y ¥ , которые отделяют области с разным типом особой точки или разным типом устойчивости, и точку (0,0) – начало координат, где соприкасаются несколько различных областей. Отметим, что границы устойчивый узел – устойчивый фокус и неустойчивый фокус — неустойчивый узел не являются бифуркационными, т.к. переход узел « фокус (без смены устойчивости) приводит к топологически эквивалентному фазовому портрету (его можно получить, «изгибая» плоскость).

Для оценки «сложности» бифуркации вводится понятие «коразмерности». Коразмерность k совпадает с числом параметров, при независимой вариации которых эта бифуркация происходит. В системе происходит бифуркация коразмерности k ( codim k , dimension — размерность), если в ней выполняются k условий типа равенств. Значение k = 0 соответствует отсутствию бифуркации в данной точке. На рис. 4.11. линии представляют собой бифуркации коразмерности 1, а начало координат – бифуркацию коразмерности 2.

Бифуркации разделяют на локальные и нелокальные. Все рассмотренные нами ранее бифуркации, а также другие бифуркации смены устойчивости или исчезновения предельного множества в результате слияния с другим предельным множеством (как мы это увидим при параметрическом переключении триггера в лекции 7) – локальные. Они диагностируются с помощью линейного анализа ляпуновских показателей (собственных чисел). Нелокальные бифуркации нельзя определить на основе линейного анализа окрестности стационарного состояния, здесь требуется нелинейный анализ системы. К нелокальным бифуркациям относятся образование сепаратрисных петель, касание аттрактором сепаратрисных кривых или поверхностей.

Бифуркации аттракторов принято подразделять на мягкие (внутренние) бифуркации и кризисы (жесткие бифуркации). Внутренние бифуркации приводят к топологическим изменениям самих притягивающих множеств, не затрагивая их бассейнов притяжения – областей, из которых фазовые траектории сходятся к данному аттрактору.

Кризисы – бифуркации аттракторов, сопровождающиеся качественной перестройкой границ областей притяжения (бассейнов) аттракторов. Пример — бифуркация слияния устойчивого узла с седлом, в результате чего аттрактор исчезает (рис. 6.5).

Часто кроме бифуркационных диаграмм для наглядности строят фазопараметрические диаграммы. В этом случае по одним координатным осям откладывают значения параметров, а по другим – динамические переменные или связанные с ними величины. Получают некоторую гиперповерхность, точки которой соответствуют определенным динамическим режимам, меняющимся с изменением параметров. Бифуркации на таких диаграммах могут проявляться в образовании складок поверхности или в расщеплении ее на несколько частей.

Резкие значительные изменения переменных состояния динамической системы, вызванные малыми возмущениями в правых частях уравнений, в частности, малыми изменениями параметров, часто называют катастрофами. Теория катастроф была развита топологом Рене Тома ( Thom R . Structural Stability and Morphogenesis . N . Y ., 1972). В основу ее была положена разработанная ранее теория особенностей Уитни. Показано, что существует небольшое количество элементарных катастроф, с помощью которых можно локально описать поведение системы. С основами теории катастроф можно познакомиться по книге: В.И. Арнольд. Теория катастроф. М., Изд. МГУ, 1983.

Для описания событий, происходящих вблизи бифуркационной границы удобно использовать системы самых простых уравнений, обычно – полиномиальных, которые описывают качественные особенности процесса. Такие системы называются модельными и активно используются в теории бифуркаций и в теории катастроф. Например, для системы, которая может быть описана одним автономным дифференциальным уравнением, модельная система имеет вид:

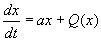
Условием вырождения (бифуркации) является равенство нулю коэффициента a , то есть отсутствие в правой части линейного члена.

В качестве модельной системы, описывающей бифуркацию коразмерности k , обычно выступает полиномиальная система l £ k уравнений, зависящая от k малых параметров. При нулевых значениях параметров в системе возникает вырождение, а при вариации параметров происходит бифуркация. В простейшем случае в качестве параметров выступают вещественные части собственных чисел. Размерность модельной системы l совпадает с количеством собственных чисел, вещественные части которых обращаются в нуль при бифуркационном значении параметра a .

Рассмотрим основные бифуркации – катастрофы.

Седло-узловая бифуркация (складка).

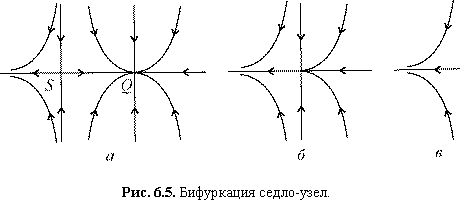
Пусть в системе при a a * существуют два состояния равновесия: устойчивый узел Q и седло S (Рис. 6.5, а). При a = a * происходит слияние узла и седла с образованием негрубого состояния равновесия, называемого седло-узлом . (рис. 6.5, б).

При a > a * положение равновесия исчезает (рис. 6.5, в). Переменная x с течением времени стремится к бесконечности. Поскольку в результате бифуркации аттрактор (узел) исчезает, границы бассейнов должны качественно перестроиться. Следовательно, данная бифуркация является кризисом (катастрофой). Простейшая модельная система, описывающая данную бифуркацию, имеет вид:

Рис. 6.5. Бифуркация седло-узел .

(6.17)

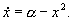
Уравнение (6.17) имеет два стационарных состояния

Линеаризуем уравнение (6.17) в окрестности стационарного состояния. Собственные значения

.

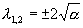
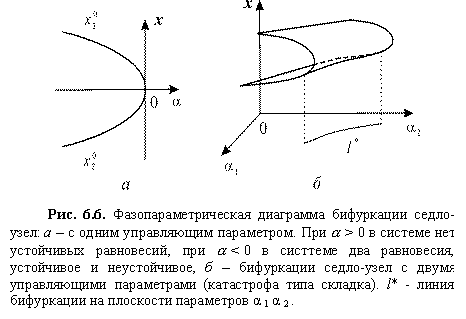
Таким образом ` x <sub>1</sub> — устойчивое состояние, ` x ₂ —неустойчивое. При a = 0 имеем ` x <sub>1</sub> = ` x ₂ = 0 , и собственное значение в этой точке равно нулю. Бифуркация имеет коразмерность 1, так как выделяется одним условием l ( a )= 0. На рис. 6.6 а изображена фазопараметрическая диаграмма системы (6.17). Если бифуркация седло-узел происходит в двупараметрической системе, то в фазопараметрическом пространстве ей соответствует особенность (катастрофа) типа складки вдоль линии l * на плоскости параметров.

Рис. 6.6. Фазопараметрическая диаграмма бифуркации седло-узел: а – с одним управляющим параметром. При a > 0 в системе нет устойчивых равновесий, при a 0 в систтеме два равновесия, устойчивое и неустойчивое, б – бифуркации седло-узел с двумя управляющими параметрами (катастрофа типа складка). l * — линия бифуркации на плоскости параметров α ₁ α ₂ .

Поясним, как можно пользоваться образами теории катастроф при изучении математических моделей на примере модели второго порядка, содержащей переменные x и u . u – это фактически управляющий параметр a , бифуркационному значению которого a = a * соответствует u = 0.

Пусть x – «быстрая» переменная, но исключить ее нельзя, поскольку система не удовлетворяет условиям Теоремы Тихонова (см. выше), так как быстрый процесс не везде устойчив. «Складка» соответствует модели

(6.18)

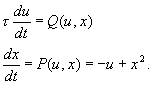
Здесь t >> 1, характерное время изменения переменной x будем считать порядка единицы. Изоклина P = 0 имеет устойчивую ветвь – аттрактор в форме «складки». При медленном уменьшении u в соответствии с первым уравнением (6.18) при достижении u = 0 произойдет срыв изображающей точки, которая либо уйдет на ¥ , либо перескочит на другой устойчивый аттрактор. Заметим, что в реальных моделях такая устойчивая ветвь всегда присутствует.

Катастрофа типа «складки» появляется в моделях, описывающих релаксационные колебания, «ждущие» режимы и триггерные системы (параметрическое переключение). В распределенных моделях (2 том лекций) модели, имеющие «складки», используются при описании автоволновых процессов и диссипативных структур.

Трехкратное равновесие (сборка)

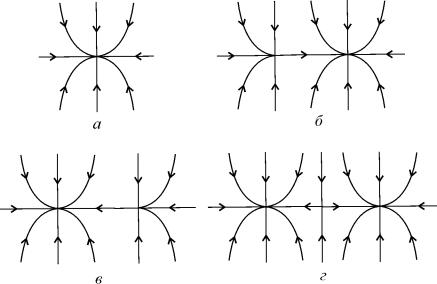
Бифуркация состоит в слиянии трех состояний равновесия – узлов Q ₁, Q ₂ и седла Q ₀ между ними (в рождении двух устойчивых узлов из седла) (рис. 6.7, 6.8)

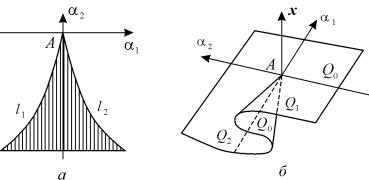
Рис. 6.7. Трансформации фазового портрета при бифуркации «рождение двух узлов из седла». а – фазовый портрет в незаштрихованной области (рис. 6.8 а); б – фазовый портрет на границе l ₁ ; в – фазовый портрет на границе l ₂ ; в – фазовый портрет в заштрихованной области представлен двумя устойчивыми узлами и седлом между ними.

Рис. 6.8. Бифуркация трехкратного равновесия (катастрофа – сборка).

а — бифуркационная диаграмма, б – фазопараметрическая диаграмма

Бифуркация имеет коразмерность 2 и требует для своего описания как минимум двух параметров. Модельной системой для нее служит уравнение:

(6.19)

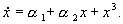
Система имеет три особых точки. Линейный анализ показывает, что при a ₂> 0 и любом a ₁ система имеет единственное состояние равновесия Q ₀ с отрицательным собственным значением, то есть асимптотически устойчивое. При a ₂ существует область значений a ₁ (заштрихованная область на бифуркационной диаграмме (рис.6.8, а), где система имеет три состояния равновесия Q ₁ , Q ₂ и Q ₀ , причем Q ₀ — неустойчивое состояние равновесия., а Q ₁ , Q ₂ — устойчивые. Такие системы (триггерные) широко применяются для описания бистабильных режимов, их модели будут подробно рассмотрены в лекции 7.

Границы области бистабильности образованы линиями l ₁ и l ₂ , соответствующими бифуркациям седло-узел, на которых два из состояний равновесия сливаются и исчезают. Линии l ₁ и l ₂ сходятся в точке А ( a ₁ = a ₂ = 0), где одновременно выполняются два условия: r ( a ₁, a ₂) в точках Q ₁ и Q ₂ одновременно равны нулю, поэтому бифуркация в этой точке, называемая трехкратным равновесием, имеет коразмерность 2. Для уравнения 6.19. в точке А фазовый портрет представляет собой седло В фазопараметрическом пространстве (рис. 6.8, б) имеет место структура, называемая сборкой. Верхний и нижний лист сборки соответствуют устойчивым состояниям равновесия, а средний – неустойчивому. На ребрах сборки имеют место катастрофы типа складки.

Модели, содержащие катастрофу типа сборки, используются при описании релаксационных автоколебаний малой амплитуды, колебательных режимов со смещением средней точки и диссипативных структур ступенчатого типа.

Слияние четырех или пяти особых точек приводит к катастрофам типа «ласточкин хвост» (рис. 6.9) и «бабочка». (Арнольд В.И. Теория катастроф. М., Знание, 1983). Фазовые пространства при этом – четырех- и пятимерные.

Отметим важное различие катастроф типа складки и сборки. «Складка» не описывает поведение системы на больших временах. Изображающая точка уходит из рассматриваемой области фазового пространства, где справедлива формула (6.18). Катастрофа складка не локализуема, то же относится к катастрофе «ласточкин хвост» с четной коразмерностью (рис. 6.9).

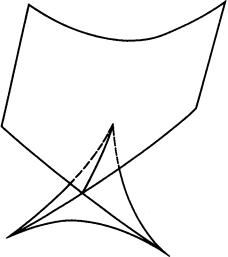
Рис. 6.9. Бифуркация «Ласточкин хвост»

В случае сборки изображающая точка остается вблизи прежнего стационарного состояния. C борка локализуема, как и катастрофа «бабочка» с четной коразмерностью.

Бифуркации, приводящие к возникновению незатухающих колебаний и квазистохастических режимов, мы рассмотрим в лекциях 8 и 10, соответственно.

Андронов А.А., Леонтович Е.А., Гордон Н.Н., Майер А.Г. Качественная теория динамических систем второго порядка. М., Наука, 1966

Арнольд В.И.. Теория катастроф. М., Изд. МГУ, 1983.

Базыкин А.Д., Кузнецов, Ю.А., Хибник А.И. Портреты бифуркаций. М., Изд. Знание, 1989

Березовская Ф.С., Карев Г.П. Дифференциальные уравнения в математических моделях, М., Изд. МИРЭА, 2000

Варфоломеев С.Д., Гуревич К.Г. Биокинетика. М., Фаир-Пресс, 1998

Лобанов А.И., Петров И.Б. Вычислительные методы для анализа моделей сложных динамических систем. М., Изд. МФТИ, 2000

Тихонов А.Н. Системы дифференциальных уравнений, содержащие малые параметры при производных. Мат. сб. т32, №3, 1952

Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М ., 1967

Thom R. Structural Stability and Morphogenesis. N . Y ., 1972.