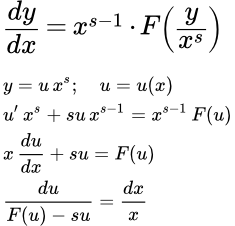Обобщенные однородные дифференциальные уравнения первого порядка
Определение
Как определить, является ли дифференциальное уравнение обобщенным однородным
Для того, чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену:
y → t α · y , x → t·x .
Если удастся выбрать такое значение α , при котором постоянная t сократится, то это – обобщенное однородное дифференциальное уравнение. Изменение производной y′ при такой замене имеет вид:
.
Пример
Определить, является ли данное уравнение обобщенным однородным:
.
Делаем замену y → t α · y , x → t·x , y′ → t α– 1 y′ :
;
.
Разделим на t α+ 5 :
;
.
Уравнение не будет содержать t , если
4 α – 6 = 0 , α = 3/2 .
Поскольку при α = 3/2 , t сократилось, то это обобщенное однородное уравнение.
Метод решения
Рассмотрим обобщенное однородное дифференциальное уравнение первого порядка:
(1) .
Покажем, что оно приводится к однородному уравнению с помощью подстановки:
t = x α .
Действительно,
.
Отсюда
; .
Подставляем в исходное уравнение (1):
;
.
Это – однородное уравнение. Оно решается подстановкой:
y = z · t ,
где z – функция от t .
При решении задач, проще сразу применять подстановку:
y = z x α ,
где z – функция от x .
Пример решения обобщенного однородного дифференциального уравнения первого порядка
Решить дифференциальное уравнение
(П.1) .
Проверим, является ли данное уравнение обобщенным однородным. Для этого в (П.1) делаем замену:
y → t α · y , x → t·x , y′ → t α– 1 y′ .
.
Разделим на t α :
.
t сократится, если положить α = – 1 . Значит – это обобщенное однородное уравнение.
Делаем подстановку:
y = z x α = z x – 1 ,
где z – функция от x .
.
Подставляем в исходное уравнение (П.1):
(П.1) ;
;
.
Умножим на x и раскрываем скобки:
;
;
.
Разделяем переменные – умножим на dx и разделим на x z 2 . При z ≠ 0 имеем:
.
Интегрируем, пользуясь таблицей интегралов:
;
;
;
.
Потенцируем:
.
Заменим постоянную e C → C и уберем знак модуля, поскольку выбор нужного знака определяется выбором знака постоянной С :
.
Возвращаемся к переменной y . Подставляем z = xy :
.
Делим на x :
(П.2) .
Когда мы делили на z 2 , мы предполагали, что z ≠ 0 . Теперь рассмотрим решение z = xy = 0 , или y = 0 .
Поскольку при y = 0 , левая часть выражения (П.2) не определена, то к полученному общему интегралу, добавим решение y = 0 .
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 03-08-2012 Изменено: 24-06-2015
Обобщенные функции и их приложения к дифференциальным уравнениям
РОССИЙСКАЯ АКАДЕМИЯ НАУК
Институт динамики систем и теории управления
Сибирского отделения Российской академии наук
Ученым советом Института
Протокол № 5 от 01.01.2001 г.
Председатель Ученого совета
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
Обобщенные функции и их приложения к дифференциальным уравнениям
Специальность 01.01.02 – «Дифференциальные уравнения, динамические системы и
1.Цели и задачи дисциплины
Цель изучения дисциплины – формирование у аспирантов углубленных профессиональных знаний о роли теории обобщенных функций в задачах естествознания.
· изучить основные операции с обобщенными функциями и их свойства;
· изучить обобщенные постановки задач Коши для обыкновенных дифференциальных уравнений и уравнений с частными производными;
· освоить с общих позиций понятие обобщенного решения дифференциального уравнения;
· подготовить аспирантов к применению полученных знаний для решения задач естествознания.
2. Место дисциплины в структуре ООП
Данная дисциплина относится к группе факультативных дисциплин (в соответствии с Федеральными государственными требованиями (ФГТ)).
Содержание дисциплины базируется на знаниях, приобретенных в курсах по теории математического анализа, теории обыкновенных дифференциальных уравнений; теории уравнений с частными производными.
3. Требования к уровню освоения содержания дисциплины.
В результате изучения дисциплины аспиранты должны:
· иметь представление об обобщенных решениях дифференциальных уравнений; об основных операциях с обобщенными функциями; об обобщенных постановках краевых задач;
· знать основную терминологию теории обобщенных функций; теоремы об аппроксимации интегрируемых и непрерывных функций с помощью бесконечно дифференцируемых; преобразование Фурье обобщенных функций; обобщенные постановки задач дифференциальных уравнений;
· уметь решать задачи, связанные с техникой действий над обобщенными функциями; доказывать свойства обобщенных функций; ставить задачи в обобщенной постановке для дифференциальных уравнений.
4. Структура и содержание дисциплины
Общая трудоемкость дисциплины составляет 3 зачетные единицы, 108 часов.
4.1. Структура дисциплины
Объем учебной работы (в часах)
Вид итогового контроля
Обобщенные функции и их приложения к дифференциальным уравнениям
Лабораторные занятия не предусмотрены.
4.2. Содержание дисциплины
4.2.1. Разделы дисциплины и виды занятий
Виды учебной работы и трудоемкость (в часах)
Обобщенные функции и действия над ними
Фундаментальные решения дифференциальных уравнений
Преобразования Фурье (основных функций; умеренных обобщенных функций; быстрорастущих обобщенных функций)
Теория Пэли-Винера. Свертка и преобразование Фурье
Проблема деления. Регуляризация. Методы вычитаний, выхода в комплексную область, метод степеней Рисса
Уравнения в выпуклом конусе. Операционное исчисление. Распространение особенностей и гладкость решений
Методы построения фундаментальных решений
Уравнения с постоянными коэффициентами в полупространстве
4.2.2 Содержание разделов дисциплины
Наименование раздела дисциплины
Обобщенные функции и действия над ними
Дифференцирование обобщенных функций. Замена переменных в обобщенных функциях. Носитель обобщенных функций. Сингулярный носитель обобщенных функций. Свертка обобщенных функций. Граничные значения аналитических функций. Пространство умеренных распределений.
Лекции, самостоятельная работа
Фундаментальные решения дифференциальных уравнений
Фундаментальные решения. Примеры фундаментальных решений. Распространение волн. Построение фундаментальных решений обыкновенных дифференциальных уравнений. Теорема о среднем.
Лекции, самостоятельная работа
Преобразования Фурье (основных функций; умеренных обобщенных функций; быстрорастущих обобщенных функций)
Преобразование Фурье быстро-убывающих функций. Свойства преобразования Фурье. Преобразование Фурье финитных функций. Замыкание преобразования Фурье по непрерывности. Методы вычисления преобразования Фурье.
Лекции, самостоятельная работа
Теория Пэли-Винера. Свертка и преобразование Фурье
Преобразование Фурье финитных обобщенных функций. Умеренные распределения с носителем в конусе. Экспоненциально растущие распределения с носителем в конусе. Свертка и преобразование Фурье.
Лекции, самостоятельная работа
Проблема деления. Регуляризация. Методы вычитаний, выхода в комплексную область, метод степеней Рисса
Проблема деления в классах быстрорастущих распределений. Проблема деления в классах экспоненциально растущих обобщенных функций. Лестница Хермандера. Проблема деления в классах умеренных распределений.
Лекции, самостоятельная работа
Уравнения в выпуклом конусе. Операционное исчисление. Распространение особенностей и гладкость решений
Уравнения в конусе. Операционное исчисление. Дифференциально-разностные уравнения на полуоси.
Лекции, самостоятельная работа
Методы построения фундаментальных решений
Аналитическое продолжение произвольной степени многочлена второго порядка по параметру, являющемуся показателем степени. Инвариантные фундаментальные решения уравнений второго порядка с вещественными коэффициентами. Нахождение регулярной части инвариантного фундаментального решения. Построение формального фундаментального решения. Регуляризация формального фундаментального решения.
Лекции, самостоятельная работа
Уравнения с постоянными коэффициентами в полупространстве
Общее решение уравнения с постоянными коэффициентами в полупространстве. Классификация уравнений в полупространстве. Примеры уравнений параболического, гиперболического и эллиптического типов.
Лекции, самостоятельная работа
Неоднородные уравнения в полупространстве. Краевые задачи для неоднородных уравнений.
Лекции, самост. работа
5. Образовательные технологии.
Основными видами образовательных технологий дисциплины «Обобщенные функции и их приложения к дифференциальным уравнениям» являются лекции и самостоятельная работа аспиранта. Для активизации познавательного процесса слушателям даются задания по самостоятельной подготовке отдельных фрагментов лекций.
6. Учебно-методическое обеспечение самостоятельной работы аспирантов.
Используются виды самостоятельной работы аспиранта: в читальном зале библиотеки, на рабочих местах с доступом к ресурсам Internet и в домашних условиях. Порядок выполнения самостоятельной работы соответствует программе курса и контролируется в ходе лекционных занятий. Самостоятельная работа подкрепляется учебно-методическим и информационным обеспечением, включающим рекомендованные учебники и учебно-методические пособия.
7. Учебно-методическое обеспечение дисциплины
а) основная литература:
1. Владимиров математической физики. 2-е изд. – М.: Физматлит, 2004. – 400 с.
2. , Шилов функции и действия над ними. – М.: Добросвет, КДУ, 2007. – 408 с.
3. Шубин об уравнениях математической физики. – М.: МЦНМО, 2003. – 303 с.
б) дополнительная литература:
1. Владимиров функции в математической физике. – М.: Наука, 1979. –318 с.
2. Комеч уравнения в частных производных с постоянными коэффициентами // Современные проблемы математики. Фундаментальные направления. Дифференциальные уравнения с частными производными. 2. – М.: ВИНИТ, 1988. – Т. 31.
3. , Шубин дифференциальные уравнения с частными производными. Основы классической теории // Современные проблемы математики. Фундаментальные направления. Дифференциальные уравнения с частными производными. 1. – М.: ВИНИТИ, 1988. – Т. 30. – C. 5-255.
4. Шилов анализ: Второй специальный курс. – М.: Изд-во МГУ, 1984.
5. Функциональный анализ. – М.: ЛКИ, 2007. – 624 с.
2. Сайт лаборатории Параллельных информационных технологий НИВЦ МГУ www. *****
3. Электронная библиотека механико — математического факультета МГУ lib. *****
4. Электронные ресурсы издательства Springer http://link. /search? facet-content-type=%22Book%22&showAll=false
5. Электронные ресурсы издательства Elsevier http://www. info. /sciencedirect/books/subjects/mathematics
6. Национальный Открытый Университет «ИНТУИТ»- текстовые и видеокурсы по различным наукам http://www. *****/
7. Общероссийский математический портал *****
8. Видеотека лекций по математике http://www. *****/php/presentation. phtml? eventID=15&option_lang=rus#PRELIST15
9. Единая коллекция цифровых образовательных ресурсов http://school-collection. *****/catalog/rubr/75f2ec40-e574-10d2-24eb-dc9b3d288563/25892/?interface=themcol
10. Видеолекции ведущих ученых мира http://www. academicearth. org/subjects/algebra
8. Материально-техническое обеспечение дисциплины
Библиотечный фонд ИДСТУ СО РАН
Библиотечный фонд научной библиотеки ИНЦ СО РАН
Учебные классы ИДСТУ СО РАН
С общим количеством:
— рабочих мест (компьютер+монитор)
Рабочие места с выходом в интернет
Программа составлена в соответствии с требованиями следующих нормативных документов:
1. Федеральные государственные требования к структуре основной профессиональной образовательной программы послевузовского профессионального образования (аспирантура) — приказ Минобрнауки России .
2. Паспорт научной специальности 01.01.02 – «Дифференциальные уравнения, динамические системы и оптимальное управление», разработанный экспертами ВАК Минобрнауки России в рамках Номенклатуры специальностей научных работников, утвержденной приказом Минобрнауки России от 01.01.2001 г. № 59.
3. Программа-минимум кандидатского экзамена по специальности 01.01.02 – «Дифференциальные уравнения, динамические системы и оптимальное управление», утвержденная приказом Минобрнауки России «Об утверждении программ кандидатских экзаменов».
http://pandia.ru/text/79/227/66911.php