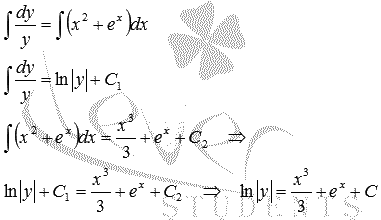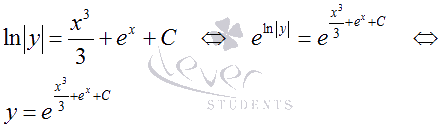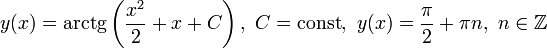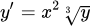Дифференциальные уравнения с разделяющимися переменными конспект урока

ПЛАН-КОНСПЕКТ ПРАКТИЧЕСКАЯ РАБОТА № 11 по дисциплине: «МАТЕМАТИКА» «Решение дифференциальных уравнений с разделяющимися переменными.»

Просмотр содержимого документа
«ПЛАН-КОНСПЕКТ ПРАКТИЧЕСКАЯ РАБОТА № 11 по дисциплине: «МАТЕМАТИКА» «Решение дифференциальных уравнений с разделяющимися переменными.»»

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ ПМР

ГОУ «ДНЕСТРОВСКИЙ ТЕХНИКУМ ЭНЕРГЕТИКИ

И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ»

Зам. директора по учебной работе

ПРАКТИЧЕСКАЯ РАБОТА № 11

по дисциплине: «МАТЕМАТИКА»

«Решение дифференциальных уравнений с разделяющимися переменными.»

Разработал преподаватель математики

ГОУ СПО «ДТЭ и КТ»

Демьянова Светлана Васильевна

на заседании ЦМК методист

_____________________ дисциплин ________ Левицкая И.Н. Протокол №__ от «__»_____201__г. «__» _________201__г.

г. Днестровск, 2019 г.

по учебной дисциплине ЕН.01. «Математика»

Тема: Решение дифференциальных уравнений с разделяющимися переменными.

Цель: Научиться решать дифференциальные уравнения с разделяющимися переменными.

Организационный момент.2 мин

Повторение теоретического материала.4 мин

Решение упражнений по образцу.9 мин.

Самостоятельное выполнение заданий. 65мин.

Подведение итогов урока, домашнее задание.

Сообщение темы урока, цели , во время урока постепенно будет использоваться тот раздаточный материал, который находится у них на столе.

Повторение теоретического материала.

1.Дайте определение дифференциального уравнения.

2. Что называют решением дифференциального уравнения?

3. Какое дифференциальное уравнение называют общим, какое в частных производных?

4. Что называют задачей Коши?

5. Какое дифференциальное уравнение называют уравнением с разделяющимися переменными.

3.Решение упражнений по образцу.

Решить дифференциальное уравнение .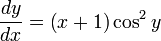

.

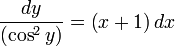
Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения:

,

.

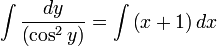
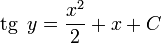
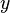
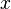
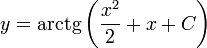
Осталось лишь выразить через :

.

Найдем также нулевые решения:

.

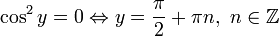
Ответ:

Выразим производную через дифференциалы:


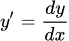
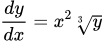
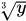
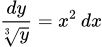
Умножим на dx и разделим на . При y ≠ 0 имеем:

Интегрируем.

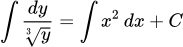
Вычисляем интегралы, применяя формулу .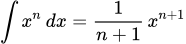



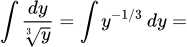
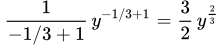
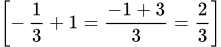
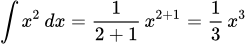
Подставляя, получаем общий интеграл уравнения
.

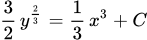
Теперь рассмотрим случай, y = 0.
Очевидно, что y = 0 является решением исходного уравнения. Оно не входит в общий интеграл .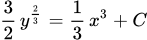
Поэтому добавим его в окончательный результат.

; y = 0.

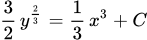
Пример 4. Найти частное решение уравнения (1+e 2x )y 2 y’=e x , удовлетворяющее начальному условию y(0)=1

Запишем данное уравнение в дифференциальной форме: (1+e 2x )y 2 dy-e x dx=0. Теперь разделим переменные: y 2 dy- dx=0 Проинтегрируем последнее уравнение:

Получили общее решение исходного уравнения. Использовав начальное условие, определим значение произвольной постоянной: dy-

Следовательно, частное решение исходного уравнения имеет вид dy-

4.Самостоятельное выполнение заданий.

Индивидуальное задание по порядковому номеру в журнале, т.е в задании вместо N студент подставляет свой порядковый номер.

Решить дифференциальные уравнения и найти частные решения.

5. Подведение итогов урока, домашнее задание.

Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»

Разделы: Математика

I. Обыкновенные дифференциальные уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение

1. Рассмотрим дифференциальное уравнение первого порядка

Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение, получим: , – тождество.

А это и значит, что функция – есть решение этого дифференциального уравнения.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

1.Найти частное решение дифференциального уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения, получим

Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .

— общее решение дифференциального уравнения.

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.

Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .

Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.

2. Найти общее решение дифференциального уравнения

Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .

Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .

Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x₀) = y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x₀) = y₀,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого порядка

2.1. Основные понятия

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.

Пример. Рассмотрим дифференциальное уравнение первого порядка .

Решением этого уравнения является функция .

Действительно, заменив в данном уравнении, его значением, получим

то есть 3x=3x

Следовательно, функция является общим решением уравнения при любом постоянном С.

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим откуда C = 0.

Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.

2.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x) и g(y)– заданные функции.

Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».

Уравнение вида называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными

1. Производную функции переписать через её дифференциалы
2. Разделить переменные.
3. Проинтегрировать обе части равенства, найти общее решение.
4. Если заданы начальные условия, найти частное решение.

Решить уравнение y’ = xy

Решение. Производную функции y’ заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Найти частное решение уравнения

Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда

Интегрируя обе части последнего равенства, найдем

Подставив начальные значения x₀ = 1, y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл будет или

Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися переменными. Разделив переменные, получим:

Проинтегрировав обе части уравнения, получим:

Используя начальные условия, x = 2 и y = — 3 найдем C:

Следовательно, искомое уравнение имеет вид

2.3. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)

где f(x) и g(x) — некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y

Если то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.

В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .

Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.

Для линейного неоднородного уравнения вида y’ = kx + b,

где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно, где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.

Алгоритм решения линейного дифференциального уравнения первого порядка

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ = u’v + uv’

3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:

5. Из скобки, приравняв ее к нулю, найти функцию

Это уравнение с разделяющимися переменными:

Разделим переменные и получим:

Откуда . .

6. Подставить полученное значение v в уравнение (из п.4):

и найти функцию Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: , т.е. .

Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0

Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’ в данное уравнение, получим

Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки

Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)

Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:

Подставим полученное значение v в уравнение Получим:

Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:

Ответ:

III. Дифференциальные уравнения высших порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0

Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C₁ и C₂.

Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.

2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: r 2 + pr +q = 0

3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ — произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде

Общее решение

Дифференцируя общее решение, получим

Составим систему из двух уравнений

Подставим вместо ,и заданные начальные условия:

Таким образом, искомым частным решением является функция

.

2. Найти частное решение уравнения

1.

1.

2. а)

2. а)

б)

б)

в)

в)

г)

г)

Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.
методическая разработка на тему

Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.

Скачать:

Предварительный просмотр:

Государственное автономное образовательное учреждение

среднего профессионального образования

Технологический колледж №28

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера

Соколова Л.А., Плотникова И.А. – преподаватели математики ГАОУ СПО города Москвы Технологический колледж № 28

Пособие для студентов 2-го курса «Методическая разработка

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера»

Соколова Л.А., Плотникова И.А. – М.: ГАОУ СПО ТК № 28. 2014. — 39 с.

В пособии представлены способы решения различных примеров по теме :Дифференциальные уравнения с разделяющимися переменными» и разобраны задачи , которых эти понятия используются. Пособие предназначено для студентов 2-го курса. Задания могут выполняться как во время самостоятельной работы на учебном занятии, так и как внеаудиторная самостоятельная работа.

ГАОУ СПО ТК № 28

Пособие для студентов 2-го курса «Методическая разработка

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера»

Данное пособие содержит теоретический материал по данной теме с подробным разбором примеров и задач и задания для самостоятельной работы на уроке или вне аудитории, может быть использовано при изучении данной темы для всех специальностей колледжа.

Дифференциальные уравнения первого порядка.

Основные понятия. Геометрический смысл.

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производную.

Так как производную можно представить в виде отношения дифференциалов, то уравнение может содержать не производную, а дифференциалы неизвестной функции и независимой переменной.

Итак, вид дифференциального уравнения первого порядка

В частных случаях в левую часть уравнения могут не входить х, либо у, но всегда входит у ’ .

Иногда дифференциальное уравнение первого порядка удается записать в виде

Решением дифференциального уравнения называется всякая функция, обращающая его в тождество при подстановке в него этой функции и ее производной взамен неизвестной функции и ее производной.

Рассмотренные ранее примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений, отличающие произвольной постоянной С, придавая которой разные числовые значения, получают разные решения.

Несмотря на то, что рассмотренные примеры носят частный характер, все-таки, не приводя доказательств, сделаем обобщение:

Любое дифференциальное уравнение имеет бесконечное множество решений, которые определяются формулой, содержащую одну произвольную постоянную. Записывать эту совокупность решений будем в виде

Общим решением дифференциального уравнения первого порядка называется совокупность его решений, определяемая формулой , где С – произвольная постоянная.

Придавая С произвольные числовые значения, можно получать частные решениг я

Замечание 1 .Получить решение в виде , т.е. искомая функция выражается через х и С в явном виде, не всегда возможно. Бывает, что решение получается в виде — неявное выражение у через х и С. В этом случае его – решение — называют общим интегралом .

Замечание 2 . Количество постоянных в общем решении дифференциального уравнения зависит от его порядка. Точнее: каков порядок дифференциального уравнения столько постоянных, причем различных, в общем решении этого уравнения.

Замечание 3. Процесс нахождения решений дифференциального уравнения иногда называют интегрированием дифференциального уравнения.

Выясним геометрический смысл как уравнения , так и его решений: общего и частного.

Итак, пусть дано обыкновенное дифференциальное уравнение . Как известно, — угловой коэффициент касательной к кривой, в нашем случае угловой коэффициент касательной, проведенной к , т.е. решению данного уравнения, в некоторой точке (х,у). Беря конкретные точки будем получать конкретные значения у ’ . Таким образом, в каждой взятой точке будет указано направление касательной к кривой, являющейся решением данного уравнения. Говорят, уравнение задает поле направлений в некоторой области.

Найти решение этого уравнения — значит найти кривую, касательная к которой в каждой ее точке совпадала бы с направлением поля в этой точке.

Таких кривых будет не одна, а целое семейство (построение можно начинать с любой точки области).

Пусть дано уравнение . Найдем значения у ’ , задавая х, у (х 0).