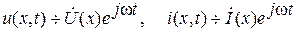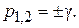Дифференциальные уравнения телеграфные однородной линии с обоснованием

Телеграфные уравнения однородной длинной линий

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Общие сведения

Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Это связано с тем, что если длина волны λ электромагнитных колебаний соизмерима с размерами цепи l, то токи и напряжения в этой одномерной цепи являются функциями двух переменных – времени t и координаты x – u(t, x), i(t, x).

Исторически первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т.е. двухпроводные линии передачи сигнала от источника к нагрузке (рис. 6. 1), длина которых l значительно превышает длину волны λ передаваемых электромагнитных колебаний. Поэтому часто эти цепи называют длинными линиями или линиями. При этом будем полагать, что конструктивные данные линии (материал и диаметр ее проводов, их взаимное расположение) и ее параметры сохраняются неизменными по длине линии. Такие длинные линии называются однородными.

Задача анализа цепей с распределенными параметрами обычно сводится к определению законов (характера) изменения токов и напряжений вдоль цепи и к исследованию частотных и временных характеристик цепи. С этой целью следует рассмотреть электрическую модель отрезка линии малой длины Δx = dx. Эта модель с достаточной точностью исследования может быть представлена электрической цепью с сосредоточенными параметрами (рис. 6.2). Всю линию можно представить как цепи с бесконечно большим числом малых по величине пассивных элементов, распределенных равномерно по ее длине.

На основании физических рассуждений можно составить следующую эквивалентную схему отрезка (рис. 6.2).

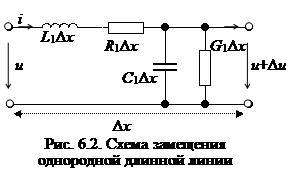
При прохождении тока вокруг проводника образуется внешнее магнитное поле, которое можно моделировать индуктивностью L₀. Она препятствует прохождению тока. Вместе с этим проводник обладает сопротивлением материала R₀. Следовательно, эти элементы должны быть соединены последовательно.

Проводники объединены конструктивно диэлектриком, который обладает конечной резистивной проводимостью G₀. Между проводниками линии создается разность потенциалов. Следовательно, вокруг проводников существует электрическое поле, накопление которого моделируется емкостью С₀.

Элементы L₀, C₀, R₀, G₀ называются параметрами линии (отрезка линии). Однако каждый отрезок линии имеет конечную длину Dx, поэтому вводятся понятия погонных параметров:

Телеграфные уравнения однородной длинной линий

Электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i(x, t) и напряжение u = u(x, t) рассматриваемой цепи являются функциями времени t и координаты x.

Составим на основе законов Кирхгофа дифференциальные уравнения для мгновенных напряжений и токов на отрезке линии длиной Δx по эквивалентной схеме на рис. 6.2.

(6.1)

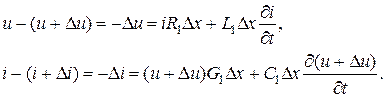
Разделив обе части уравнений (6.1) на Δx, переходя к пределу при Δx → 0 и пренебрегая величинами второго порядка малости, получим дифференциальные уравнения линии

(6.2)

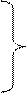
Эти уравнения в частных производных называются телеграфными, так как впервые были получены для линии телеграфной связи.

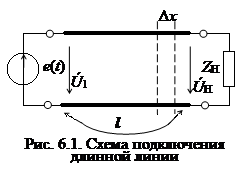
Пусть к началу линии подключен генератор гармонических колебаний e(t) = E_mcos(ωt + φ₀), а к концу линии – сопротивление нагрузки Z_H (рис. 6.1). Будем считать, что в линии имеет место режим установившихся гармонических колебаний.

Используя символический метод анализа гармонических колебаний, в котором

преобразуем уравнения (6.2) для мгновенных комплексных значений напряжения и тока

(6.3)

Здесь Z₁ = R₁ + jωL₁, Y₁ = G_{1 +} jωC₁.

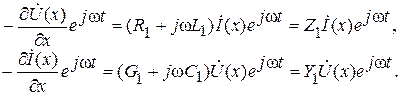
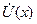
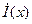
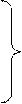
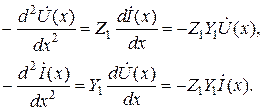
Заменим в (6.3) частную производную на полную, т.к. и не зависят от времени. Осуществим разделение переменных, т.е. выразим ток через напряжение, а напряжение через ток. Для этого продифференцируем первое уравнение по x и подставим в него второе уравнение. Получатся уравнения второго порядка

(6.4)

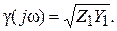
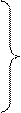
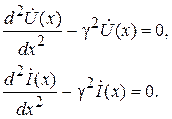
Введем обозначение Этот коэффициент называют коэффициентом распространения. Перепишем систему (6.4) в окончательном виде:

(6.5)

Уравнения (6.5) называются телеграфными уравнения однородной линии в комплексной форме. Они являются однородными, 2-го порядка, линейными (т.к. Z₁ и Y₁ не зависят от x).

Корни характеристического уравнения p 2 – γ 2 = 0 системы (6.5) равны

Общее решение первого уравнения системы (6.5) для напряжения в произвольной точке x линии ищем в виде

. (6.6)

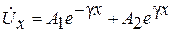
Из первого уравнения системы (6.3)

.

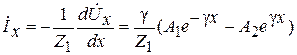
Введя еще одно обозначение

– волновое сопротивлении, (6.7)

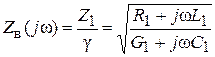
запишем решение для тока в точке x в форме

. (6.8)

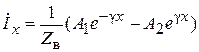
Постоянные интегрирования A₁ и A₂ можно найти из начальных условий:

при x = 0 Ú_x = Ú₁ и Ì_x = Ì₁, где Ú₁ и Ì₁ – напряжение и ток в начале линии. Тогда из (6.6 и 6.8) для x:

Подстановка полученных значений постоянных интегрирования в (6.6, 6.8) дает следующие уравнения для определения напряжении Ú_x и тока Ì_x в произвольной точке x длинной линии

(6.11)

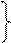
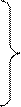
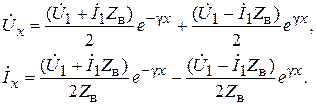
Выражения (6.11) называют уравнениями передачи длинной линии.Они позволяют рассмотреть распределение напряжений и токов в однородной длинной линии в произвольной точке x.

Дата добавления: 2016-11-02 ; просмотров: 4538 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Решение системы телеграфных уравнений относительно напряжения и тока для однородной двухпроводной линии

Руслан Сукин 4 лет назад Просмотров:

1 Решение системы телеграфных уравнений относительно напряжения и тока для однородной двухпроводной линии Постановка задачи Пусть имеется однородная двухпроводная линия, к началу которой подключен идеальный источник синусоидальной ЭДС, а к концу — резистивная нагрузка Z 2 = 0,2 ком. Исходные данные: l = 2 км — длина линии; r 0 = 0.2 ком/км — сопротивление пары проводников, отнесённое к единице длины линии; L 0 = 1 мгн/км — индуктивность на единицу длины линии; g 0 = 0 — проводимость утечки на единицу длины линии (здесь предполагается, что изоляция идеальная); C 0 = 25 нф/км — ёмкость на единицу длины линии; — напряжение в начале линии (циклическая частота рад/мкс, частота f = 500 кгц); Z 2 = 0,2 ком — сопротивление нагрузки в конце линии (линия работает на активную нагрузку). В момент времени t = 0 к началу линии подключается идеальный источник ЭДС, мгновенное значение которой равно u 1 ( t ). В момент подключения источника во всех сечениях линии токи и напряжения были равны нулю (задача с нулевыми начальными условиями). Электромагнитные процессы в линии описываются системой телеграфных уравнений относительно напряжения и тока: (1) Для удобства моделирования в системе FEMLAB систему уравнений (1) запишем в матричной форме: (2) Моделирование в GUI-приложении femlab Запуск femlab приведёт к развёртыванию окна Навигатора моделей с раскрытой закладкой New. Навигатором моделей выберем прикладной режим 1 D / PDE modes/ Coefficient/ Time dependent, нажмём кнопку More.В строку редактирования Dependent variables впишем: u ii. Это означает, что искомая функция u ( x, t )(напряжение) в (1) и (2) в модели femlab будет обозначаться именем u, а функция i( x, t) (ток) — именем ii. Нажатие кнопки OK приведёт к закрытию Навигатора моделей и переводу GUI femlab в одномерный режим моделирования. Моделирование начинается с режима Draw Mode. В этом режиме прорисовывается геометрия расчётной области. Для создания геометрического объекта, соответствующего линии, выполним команду меню Draw / Specify Geometry, которая разворачивает диалоговое окно, изображённое на рис. 1. Введённые в диалоговое окно числовые

2 значения означают следующее: началом линии является точка с координатой x = -1 км, а концом — точка x = +1 км. Нажатие кнопки OK приведёт к закрытию окна и созданию солидного одномерного объекта. Рис. 1. Диалоговое окно создания геометрического объекта. Когда объект создан, можно перейти в режим задания граничных условий Boundary Mode. В этом режиме выполним команду меню Boundary / Boundary Settings. Эта команда разворачивает диалоговое окно ввода и редактирования граничных условий (ГУ). Окно показано на рис. 2. Рис. 2. Диалоговое окно ввода и редактирования граничных условий В диалоговом окне, изображённом на рис. 2, точка 1 — начало линии, точка 2 — конец линии. Если в задаче моделирования количество зависимых переменных больше одной, то диалоговое окно редактирования граничных условий состоит из шести закладок, четыре из которых предназначены для ввода матриц ГУ. В нашем случае с помощью этих матриц можно задать режим питания линии и режим нагрузки. Сначала опишем режим питания линии. Для этого выделим точку 1, тип ГУ — Дирихле. В закладки q и g заходить не обязательно, т.к. там стоят нули по умолчанию. Значения, которые нужно ввести для точки 1, показаны на рис. 3, 4, 5.

3 Рис. 3. Матрица коэффициентов условия Дирихле в случае задания идеального источника ЭДС Рис. 4. Матрица правой части ГУ Дирихле, если в данную точку линии включен источник Рис. 5. Матрица коэффициентов ГУ Дирихле, если в данную точку (конец) линии включен резистор

4 Матрицу r для точки 2 зададим равной нулю. Следует обратить внимание также на то, что определитель матрицы h в начале и в конце линии равен нулю. Теперь можно переходить в режим Subdomain Mode и вводить числовые значения параметров линии. Команда меню Subdomain / Subdomain Settings раскрывает диалоговое окно Subdomain Settings, состоящее из десяти закладок (рис. 6). Поскольку уравнения (1), (2) содержат дифференциальные операторы первого порядка, матрицу c примем равной нулю (рис. 6). Рис. 6. Диалоговое окно ввода коэффициентов PDE Остальные матрицы введём в соответствии с уравнением (2): ; ; ; ; ;. В закладке Element по умолчанию выбраны Лагранжевы элементы второго порядка. С помощью команды меню Mesh / Mesh Mode перейдём в режим построения конечноэлементной сетки. Автоматически расчётная область будет разбита на 15 элементов. Это очень грубая сетка для решения поставленной задачи. Командой меню Mesh / Refine Mesh переопределим конечноэлементную сетку. Теперь расчётная область будет разбита на 30 элементов. Это также слишком грубо. Будем выполнять команду Mesh / Refine Mesh до тех пор, пока количество элементов не достигнет 120. Командой меню Solve / Parameters раскроем диалоговое окно настройки параметров решателя. Раскроем в этом окне закладку Timestepping. В строку редактирования Output times введём 0:0.1:20 (рис. 7) и нажмём OK. Остальные параметры оставим по умолчанию. Командой меню Solve / Solve Problem запустим краевую задачу на выполнение.

5 Рис. 7. Диалоговое окно настройки параметров решателя (закладка >Timestepping) Визуализация решения После завершения решения GUI femlab переходит в режим визуализации. Для одномерных задач возможно три режима визуализации: показ функции решения в фиксированные моменты времени, анимация, показ решения в линейном или точечном сечении расчётной области. Первые два режима настраиваются командой меню Post / Plot Parameters. Эта команда развёртывает диалоговое окно, вид которого показан на рис. 8. Ниспадающее меню Solution at time позволяет выбрать требуемый момент времени моделирования для показа функции решения. На рис. 9 показано распределение напряжения в линии спустя 9 микросекунд с момента подключения источника к линии. Видно, что в этот момент времени волна напряжения ещё не достигла конца линии.

6 Рис. 8. Диалоговое окно настройки параметров визуализации решения Рис. 9. Распределение напряжения в линии в момент времени t = 9 мкс Если нам надо показать распределение тока в линии, то в закладке Curve диалогового окна Plot Parameters в ниспадающем меню Y expression нужно выбрать ii ( ii ). Распределение тока (в миллиамперах) в тот же момент времени показано на рис. 10.

7 Рис. 10. Распределение тока в линии в момент времени >t = 9 мкс Значительный интерес представляет также визуализация решения в линейном сечении расчётной области. Пусть для простоты линейное сечение представляет собой всю расчётную область. Данный вид визуализации может осуществляться в двух режимах: 1) отображение в фигуре MATLAB семейства графиков выбранной функции решения в указанные моменты времени, 2) отображение трёхмерного поверхностного графика, одной координатной осью которого является время. Попробуем проиллюстрировать последний из этих режимов. По команде меню Post / Cross — Section Plot Parameters разворачивается диалоговое окно настройки параметров режимов визуализации в сечениях расчётной области (рис. 11). В закладке General выделим все позиции списка Solution at time. В закладке Line выделим зону 1 расчётной области (в данной задаче она всегда является выделенной). Установим в этой же закладке флажок Connect lines to surface и нажмём кнопку OK. В фигуре MATLAB будет нарисовано изображение пространственно-временного распределения интересующей нас функции решения. Распределение напряжения в линии показано на рис. 12.

8 Рис. 11. Диалоговое окно настройки параметров режимов визуализации в сечениях Рис. 12. Пространственно-временное распределение напряжения в линии На рис. 12 отчётливо видна конечная скорость распространения волны напряжения. Следует также обратить внимание на то, что при исходных данных, записанных выше, практически незаметно отражение волны от конца линии. Такое явление наблюдается потому, что линия нагружена на сопротивление, очень близкое к волновому

9 сопротивлению линии. Теперь исследуем поведение волны при различных режимах нагрузки линии. Отражение волн напряжения и тока в режиме холостого хода и короткого замыкания на конце Чтобы смоделировать режим холостого хода на конце линии, вернёмся опять в режим Boundary Mode. В точке 2 зададим h 22 = 1, остальные коэффициенты матрицы h зададим равными нулю. Повторим расчёт напряжения и тока в линии. На рис. 13 показано распределение напряжения в линии в момент времени t = 13.5 мкс. На рис распределение тока в тот же момент времени. Рис. 13. Распределение напряжения в линии в момент времени t = 13.5 мкс

10 Рис. 14. Распределение тока в линии в момент времени t = 13.5 мкс Пространственно-временное распределение напряжения в линии показано на рис. 15, а тока — на рис. 16. Эти трёхмерные графики можно вывести в разные фигуры MATLAB, если перед выполнением команды построения графика воспользоваться функцией figure. Это бывает полезно при необходимости сопоставления графиков. Следует обратить внимание на то, что в любой момент времени ток в конце линии равен нулю.

11 Рис. 15. Пространственно-временное распределение напряжения в режиме холостого хода на конце Рис. 16. Пространственно-временное распределение тока в режиме холостого хода на конце Чтобы смоделировать режим короткого замыкания на конце линии, вернёмся опять в режим Boundary Mode. В точке 2 зададим h 11 = 1, остальные коэффициенты матрицы h зададим равными нулю. Повторим расчёт напряжения и тока в линии. Пространственно-

12 временное распределение напряжения в линии показано на рис. 17, а тока — на рис. 18. Следует обратить внимание на то, что в любой момент времени напряжение в конце линии равно нулю. Рис. 17. Пространственно-временное распределение напряжения в режиме короткого замыкания на конце Рис. 18. Пространственно-временное распределение тока в режиме короткого замыкания на конце

13 Реактивная нагрузка на конце линии Опять перейдём в режим Boundary Mode и выполним команду меню Boundary/ Boundary Settings. Чтобы смоделировать индуктивную нагрузку в конце линии, нужно в диалоговом окне Boundary Settings выбрать точку 2, обнулить для этой точки матрицы h и r, заполнить первый столбец матрицы q единицами. Остальные элементы матриц q и g должны быть равны нулю. Далее нужно открыть закладку Weak диалогового окна Boundary Settings и вписать в строку редактирования dweak выражения — u_test*0.3*ii_time -ii_test*0.3*ii_time Эти выражения соответствуют индуктивности нагрузки, равной 0.3 мгн. После ввода граничных условий, соответствующих индуктивной нагрузке, можно запускать вычисления. Для проверки правильности моделирования индуктивной нагрузки выведем в две фигуры MATLAB графики напряжения и тока в конце линии. Развернём диалоговое окно Cross — Section Plot Parameters и раскроем закладку Point. В этой закладке включим радиокнопку Point plot, в рамке Select point via включим радиокнопку Vertices, в списке выберем точку 2. В строку редактирования Point plot впишем имя u. В фигуру 1 будет выведен график напряжения в конце линии. Аналогичную операцию проведём для тока (имя зависимой переменной ii ), предварительно выполнив оператор MATLAB figure (2). Графики напряжения и тока в конце линии показаны на рис. 19, 20. По графикам видно, что синусоидальная составляющая тока отстаёт от напряжения на четверть периода, т.е. индуктивная нагрузка смоделирована правильно. Рис. 19. График напряжения в конце линии

14 Рис. 20. График тока в конце линии Пространственно-временное распределение напряжения и тока в линии показано на рис. 21, 22. Как видно, от индуктивной нагрузки волны напряжения и тока отражаются почти так же, как и от разомкнутого или короткозамкнутого конца. Кроме того, индуктивная нагрузка обуславливает наличие непериодической составляющей тока в линии и в нагрузке. Особенно хорошо это видно на рис. 20. Рис. 21. Пространственно-временное распределение напряжения

15 Рис. 22. Пространственно-временное распределение тока Аналогичным способом можно смоделировать ёмкостную нагрузку в конце линии. Однако это практически не удаётся из-за абсолютной неустойчивости получаемой вычислительной модели.

Длинная линия

Длинная линия

Содержание

1 Дифференциальные уравнения длинной линии
1.1 Погонные параметры 1.2 Эквивалентная схема участка длинной линии 1.3 Телеграфные уравнения 1.4 Условие регулярности линии 1.5 Однородные волновые уравнения длинной линии 1.6 Распределение поля падающей волны

2 Комплексный коэффициент отражения по напряжению 3 Коэффициенты бегущей и стоячей волны 4 Входное сопротивление длинной линии 5 Режимы работы длинной линии

5.1 Режим бегущей волны 5.2 Режим стоячей волны 5.3 Режим смешанных волн

6 Линия без потерь

6.1 Разомкнутая линия 6.2 Замкнутая линия 6.3 Ёмкостная нагрузка 6.4 Индуктивная нагрузка 6.5 Активная нагрузка 6.6 Комплексная нагрузка

7 КПД линии с потерями 8 Пределы применимости теории длинной линии 9 См. также 10 Примечания

Длинная линия — регулярная линия передачи[1], длина которой превышает длину волны (λ) колебаний, распространяющихся в линии.

Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

Дифференциальные уравнения длинной линии

Рассмотрим двухпроводную длинную линию, представленную на рисунке 1. На рисунке обозначено: ZН = RН + iXН — комплексное сопротивление нагрузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.

Погонные параметры

Рис.1 — К выводу дифференциальных уравнений длинной линии

Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами:

R1 — погонное сопротивление, Ом/м; G1 — погонная проводимость, 1/Ом м; L1 — погонная индуктивность Гн/м; C1 — погонная ёмкость Ф/м;

Погонные сопротивление R1 и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов[2] и в диэлектрике, тем меньше соответственно, R1[3] и G1[4]. Погонные индуктивность L1 и емкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

Эквивалентная схема участка длинной линии

Рис.2 — Эквивалентная схема участка длинной линии

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему, покзанную на рисунке 2. На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz. Значения параметров схемы определяются соотношениями:

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

Подставляя сюда значения параметров схемы из (1), получаем:

,

где Z1 = R1 + iωL1, Y1 = G1 + iωC1 — погонные комплексные сопротивление и проводимость линии. Из последних соотношений находим дифференциальные уравнения линии:

Телеграфные уравнения

Основная статья: Телеграфное уравнение

Эти соотношения называются телеграфными уравнениями длинной линии. Они определяют связь между током и напряжением в любом сечении линии. Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:

При этом учтем, что:

Условие регулярности линии

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии ее погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии

,

где γ — коэффициент распространения волны в линии: .

Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

,

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (3.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое — отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1).Так, например, для падающих волн напряжения и тока можно записать:

,

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

,

где α — коэффициент затухания волны[5] в линии; β — коэффициент фазы[6]. Тогда соотношение (7) можно переписать в виде:

.

Так как при распространении падающей волны на длину волны в линии λЛ фаза волны изменяется на 2π , то коэффициент фазы можно связать с длиной волны λЛ соотношением

.

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

.

Определим коэффициенты A и B , входящие в решения (6) волновых уравнений, через значения напряжения UН и тока IН на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

,

где — волновое сопротивление линии[7].

Перепишем (6) с учетом (12):

.

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в конце линии z = 0:

.

Тогда из (13) при z = 0 найдем

,

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

.

При выводе (15) учтены определения гиперболических синуса и косинуса[8].

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует[9]. Тогда в (6) следует положить BU = 0, BI = 0:

.

Распределение поля падающей волны

Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза

На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU апряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α[5] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α[5] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α[5] = 0. Тогда напряжение в линии можно представить в виде:

,

где Γ = BU / AU — комплексный коэффициент отражения по напряжению.

Комплексный коэффициент отражения по напряжению

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах:

| Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[9]; | Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;

Соотношение (16) представляет собой сумму падающей и отраженной волн.

Рис.4. Векторная диаграмма напряжений в линии с отраженной волной

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

.

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

.

Если линия нагружена на сопротивление, для которого |Г| = 1 , т. е. амплитуда падающей и отраженной волн равны |BU| = |AU|, то в этом случае Umax = 2|AU|, а Umin = 0.

Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Коэффициенты бегущей и стоячей волны

По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — kБВ и коэффициента стоячей волны kСВ:

Эти коэффициенты, судя по определению, изменяются в пределах:

,

.

На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.

Входное сопротивление длинной линии

Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:

Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.

Режимы работы длинной линии

Различают три режима работы линии:

режим бегущей волны; [10] режим стоячей волны; [10] режим смешанных волн.

Режим бегущей волны

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[10].

Режим стоячей волны

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей BU = AU т. е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = , kбв = 0[10].

Режим смешанных волн

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 W Сопротивление нагрузки меньше волнового сопротивления линии RН