Дифференциальные уравнения теплопроводности для анизотропных тел

Уравнение теплопроводности для анизотропного тела с источником энергии и переменными теплофизическими параметрами

Из обширного класса анизотропных тел рассмотрим такие, в которых тело имеет различные коэффициенты теплопроводности 2jc, Ху, Xz в трех взаимно перпендикулярных направлениях, принятых за оси координат х, у, z. Если принять это ограничение, то останется справедливой запись закона Фурье в форме (1.2). Предположим, что в объеме AV= AxAyAz могут находиться источники тепла, удельная мощность которых в момент

времени г равна W(x, у, z, г), Вт/м (рис.2.1).

Рассмотрим изменение теплового состояния объема AV за промежуток времени dx. При этом будем базироваться на двух законах: законе сохранение энергии и законе Фурье.

Количество тепла, поступающего в объем слева через поверхность AyAz за время dr, обозначим dQx, а количество тепла, выходящее из объема AV через правую поверхность AyAz, обозначим dQ’x. Аналогично введем обозначения dQy, dQ’y, dQz, dQ’z, Пусть за время dr температура t( х, у, z, т ) объема А V повысилась на dt градусов, тогда количество тепла, поглощенное объемом, равно cpAVdt; действие источников тепла вызовет дополнительное поступление энергии, равное WA Vdr.

На основании закона сохранения энергии:

dQx + dQy + dQ, + WAVdr = dQ’x+dQ’y +dQ’z+cpA Vdt, (2.1)

Рис. 2.1. К выводу дифференциального уравнения теплопроводности На основании закона Фурье имеем

Уравнение теплопроводности

Уравнение теплопроводности

• В данном разделе приводится вывод уравнений теплопроводности в виде дифференциальных уравнений в декартовых системах координат. Наиболее удобна дифференциальная форма уравнения теплопроводности. Тепловое уравнение изотропного материала. Рассмотрим бесконечно малое пространство с размерами Dx, boo, bg, iso -. Ферментация в 3-мерной системе координат x, y, R. 2-4.It также учитывается нестационарность, то есть изменение температуры в момент времени t.

По закону теплопроводности Фурье. тепло, поступающее по оси Х в основной объем, можно описать следующим образом: dQn =- Величину теплового тока вне получить, только первые 2 части ДК разобрать Рисунок 2-4.To вывод уравнения теплопроводности. Около объем вдоль оси x, который возможен с рядом Тейлора, сохраняется в качестве достаточного приближения： приращение теплового потока, вызванного теплопроводностью в направлении x, равно: =(2-7） Как и в формулах (от 2 до 7), 2 формулы в направлениях y и 2 могут быть записаны таким же образом. Сумма приращений теплового потока — это количество тепла, которое должно накопиться в объеме. [а-(Л£ -)+£(Я5 -)+е-( «>)] ’* .

Разновидностью теплотехники является теплоэнергетика. Другим из ответвлений общей теплотехники — строительная теплотехника. Людмила Фирмаль

Если количество теплоты Q ’(x, y, z, t) в единицу времени единичного объема происходит, то накопление теплоты в основном объеме происходит следующим образом: Ох (2-9） Тепло, остающееся в элементе объема по проводимости[уравнение (2-8)] и тепло, выделяемое самим объемом [уравнение (2-9)], увеличивают тепловую энергию элемента объема. За счет такого увеличения тепловой энергии изменяется теплоемкость объемного элемента, которую можно описать следующим образом: cp8×8z / 8з -, (2-10） Где c-удельная теплоемкость. p-это плотность. X-это время. Энергетический баланс объемного элемента может быть изменен путем уравнивания изменения количества тепла объемного элемента с тепловым потоком, вызванным теплом, генерируемым теплопроводностью и самим элементом.£ ) H (x£)+£(g£)+ s’ — 2- » >Вот что следует отметить А = ч(х, гг З. ы. т)\ с = р(х, у, Z, T)и р = р (х, г, З. ы. т).

Таким образом, (2-11) справедливо для изотропных гетерогенных сред. Если можно опустить термин, обозначающий тепло в объеме(нет источника в теле), (2-11), то в проекции на 3 координатные оси можно записать как: — B + 4-10b + b(2-12) эта формула более распространена и служит в разрезе анизотропного материала. Формула(2-11) может быть упрощена при применении к изотропным однородным материалам и когда теплопроводность считается постоянной. Подобный этому Х / ФА сложно? Он имеет размерность линейного измеренного значения в квадрате, деленного на время, и называется коэффициентом температуропроводности А. характеризует свойства материала.

Тепловое уравнение цилиндрической системы координат (с использованием hi Рис. 2-5.Цилиндрическая система координат. Рисунок 2-6.Сферическая система координат. Система координат (2-13) может быть описана в более удобной форме для цилиндрической системы. Таким образом, рисунок 2-5 х = rcos6; г / = г грех б; з = з \ ДТ udChₜ1 | 1(Д1/\, м ’/ₙ1 + Р «ПФП + ДЗ) ПК (21⁴） Уравнение теплопроводности для сферической системы координат. Аналогичное преобразование сферической системы(рис. 2-6) приводит к следующей формуле: х = г sinφcos п; г = р sinφsin п; г = gsozf; ■1 Д /(&Г1d \ РТ). д / Я 1d2/ 1, м ’ ДТ [гр гду **. ГСИН у у ’ duJ ’g2sin2u ’ ПК’ (2-15） Уравнение теплопроводности анизотропного material. In в предыдущем разделе получено уравнение теплопроводности для изотропных сред.

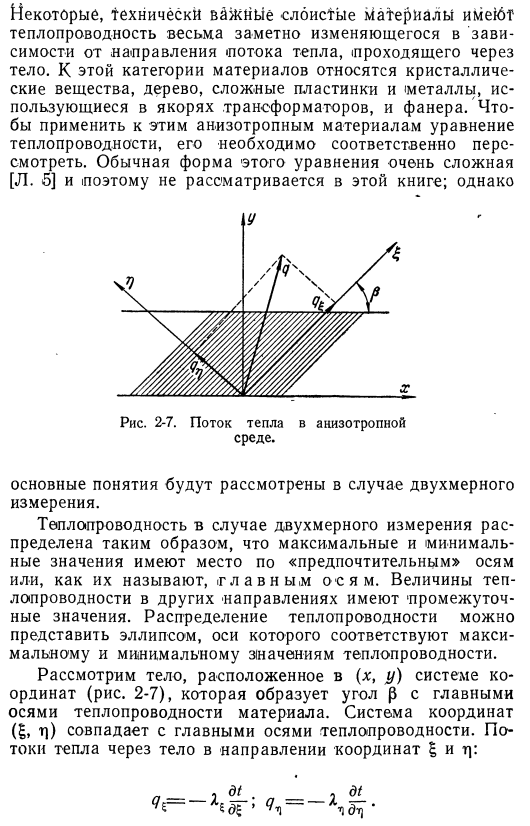
Некоторые технологически продвинутые слоистые материалы имеют теплопроводность 6Т и существенно изменяются в зависимости от направления теплового потока, проходящего через корпус. Материалы этой категории включают: кристаллический материал, древесину, составные плиты и металл используемые для анкеров в трансформаторах, и plywood. To примените уравнения теплопроводности к этим анизотропным материалам, они должны быть соответствующим образом изменены. Обычная форма этого уравнения очень сложна[L. 5], поэтому она не рассматривается в этой книге. Но、 Рисунок 2-7.Тепловой поток в анизотропной среде. Для 2-мерных измерений учитываются основные понятия. В случае 2-мерных измерений теплопроводность распределяется так, что максимальные и минимальные значения распределяются так, что они называются»приоритетной»осью или»главным валом».

• Величина теплопроводности в другом направлении имеет промежуточное значение. Распределение теплопроводности может быть представлено эллипсом с осями, соответствующими максимальному и минимальному значениям теплопроводности. представьте себе объект в системе координат (x, y) (рис.2-7). он образует угол 0 с главной осью теплопроводности материала. Система координат ( £ , m]) совпадает с главной осью теплопроводности. Тепло течет по телу в направлении координат|и Т）： −1. dt. Поток в сторону хны выглядит так: (2-16） Градиенты температуры могут быть преобразованы в градиенты X и y с помощью следующих соотношений: ДТ dt ДХ ИДТ сделать df «dhdG «’ duod ^’ ДТ _ _ _ _ д / ДХ. д / д Дри ДХ ДТ] ’у д（\ И в соответствии с геометрией фигуры Р / = грешить£= — qcosp; х = $ КГУ = —qsinp.

Если подставить эти значения в Формулу (2-16) и преобразовать ее, то получится тепловой поток. Ях = — потому что₽+ грехах ’ п)^ — (iₜ— потому что грех п п; Общая форма теплового потока [уравнение (2-12)] уравнение теплопроводности [уравнение (2-17)] может быть использовано для описания двумерного уравнения теплопроводности анизотропного материала в следующем виде: 57 = \ COS в ’п + грехах’ п） +(sinsinр+ x, cosp)g +(я£-X₄)sin2pd.(2

18） Для изотропных сред L.= LT. и p =0.In при этих условиях уравнение(2-18) сводится к 2-мерному уравнению(2-13). Если пластины из анизотропного материала зажаты между изотермическими поверхностями испытуемой теплопроводной системы, и Образец готовят таким образом, что его главная ось образует изотермическую поверхность и угол р, после чего определяют измеренную теплопроводность (в зависимости от того, была ли она выполнена вдоль направления x или y). Xia3 как COS Ильин; = грех₽ — ч cos3.

Теоретическими разделами теплотехники, в которых исследуются законы превращения и свойства тепловой энергии, а также процессы распространения теплоты являются техническая термодинамика и теория теплообмена. Людмила Фирмаль

Если геометрическая ось анизотропного тела совпадает с главной осью теплопроводности, то уравнение (2-18） Упрощенный: д / ч-л ч мск Для древесины с различной теплопроводностью по окружности 0, вдоль волокна z, вдоль волокна g идея формулы(2-19) может быть применена следующим образом: Рисунок 2-8.Вектор теплового потока слоистого материала. Уравнение(2-14) помещает ось z вдоль линии центра дерева, игнорируя термин, обозначающий источник тепла. Поэтому в цилиндрических координатах (2-20） Пример 2-1.Пластина из слоистого материала (пластина) используется для экспериментов по теплопроводности. Слой под углом с гладкой поверхности образца(рис. 2-8).

Поверхность A является изотермической поверхностью для поддержания постоянной, но разной temperature. It необходимо рассчитать угол, который складывается за счет тепла N потоков, перпендикулярных изотермической плоскости. ЮЖД рис. 2-8, С ^ С ^ А ДТ / ДТС тгт〜\ ДТ / дл■ Но основываясь на предыдущих расчетах dt. В. С.?^⁺сентенция ДТ. Сделать это. ДТ, ДТ. «Чо?»ДТ⁺ы? В. Отсюда ATⱼ[соз£(ДТ [ды) — грех п(dtjdx)] у- ^ [что? (dtfdx) — грех п (dtjdy）] * (ля） Однако в системе, которую мы рассмотрим здесь, интерфейс остается изотермическим. То есть координатная ось y находится в направлении перпендикуляра n, а x — в изотермическом plane. So, d / / dx = 0, Формула (a)принимает вид: тгр = ^ — Ctgf = ^ ТГА. Таким образом, y a, А Вектор теплового потока не перпендикулярен изотермической плоскости, как в случае, когда материал является изотермическим. Если X ^ * = = 2X ^ среда-это дерево и 0 = 45°、 1 tgT = » 2 -> Задачи 2-1.

Предложен способ измерения теплопроводности жидкого металла при высоких температурах temperatures. It схематически показана основная часть устройства и определена погрешность предлагаемых измерений. 2-2.Используя цилиндрическую систему координат, разложим уравнение (2-11) по модели уравнения (2-14). 2-3.Используя сферическую систему координат и малые объемные элементы этой системы координат, мы расширяем уравнение (2-15) в соответствии с моделью уравнения (2-11). 2-4. Создайте тепловое уравнение для трехмерной анизотропной среды.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальные уравнения теплопроводности для анизотропных тел

Информация

Теплопроводность твердых тел. Г.Карслоу, Д.Егер — Оглавление

Оглавление

Предисловие редактора русского перевода, 7
Из предисловия ко второму изданию, 9
Из предисловия к первому изданию, 9

Глава 1. Общая теория, 11
§ 1. Введение (11). § 2. Теплопроводность (11). § 3. Тепловой поток через произвольную поверхность (13). § 4. Изотермические поверхности (15). § 5. Теплопроводность изотропных тел (15). § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела (17). § 7. Дифференциальное уравнение теплопроводности для движущейся среды (21). § 8. Преобразование координат (23). § 9. Начальные и граничные условия (25). § 10. Безразмерные параметры (31). § 11. Экспериментальные методы определения теплопроводности (32). § 12. Математическая интерпретация начальных и граничных условий (33). § 13. Родственные дифференциальные уравнения (34). § 14. Упрощение общей задачи теплопроводности (35). § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач (39). § 16. Единственность решения задачи теплопроводности (41). § 17. Теплопроводность анизотропных твердых тел (43). § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел. (46). § 19. Теплопроводность тонкой кристаллической пластины (48). § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах. (51).

Глава 2. Линейный поток тепла. Неограниченное и полуограниченное твердое тело, 57
§ 1. Введение. Простые решения уравнения для линейного потока тепла (57). § 2. Неограниченное твердое тело. Решение Лапласа (59). § 3. Использование интегралов Фурье и преобразований Фурье (62). § 4. Полуограниченное тело с начальной температурой ƒ(х) и нулевой температурой поверхности (64). § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре φ(t) (67). § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени (70). § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна (75). § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой ƒ(t). Начальная температура равна нулю (78). § 9. Полуограниченное тело. Тепловой поток на границе х=0 является заданной функцией времени. Начальная температура равна нулю. (79). § 10. Применение полученных результатов к определению теплопроводности (82). § 11. Полуограниченное твердое тело, внутри которого находится источник тепла (82). § 12. Температура Земли и колебания температуры на ее поверхности (85). § 13. Геотермический градиент и поток тепла (87). § 14. Возраст Земли. Анализ Кельвина (89). § 15. Неограниченное составное твердое тело (91). § 16. Случай зависимости термических характеристик вещества от температуры (92).

Глава 3. Линейный тепловой поток в твердом теле, ограниченном двумя параллельными плоскостями, 97
§ 1. Введение (97). § 2. Установившаяся температура (97). § 3. Область 0 0 при других граничных условиях (285). § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом (286). § 5. Решения в цилиндрических и сферических координатах (288). § 6. Осесимметричные задачи о замерзании и плавлении (289).

Глава 12. Преобразования Лапласа. Задачи для линейного теплового потока, 292
§ 1. Исторический обзор (292). § 2. Преобразование Лапласа. Основные свойства (293). § 3. Решение уравнения теплопроводности методом преобразования Лапласа (296). § 4. Полуограниченная область x>0. Решения, получаемые из таблицы изображений (298).§ 5. Ограниченная область 0 0. Применение теоремы обращения (312). § 8. Составные твердые тела (314).