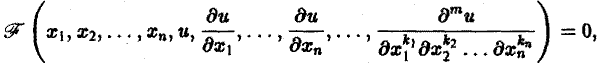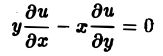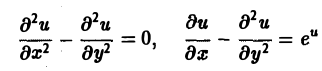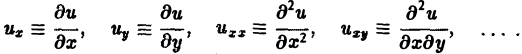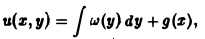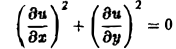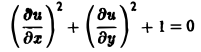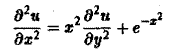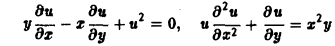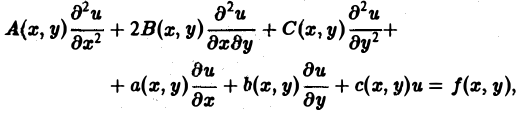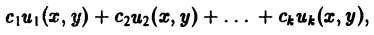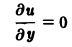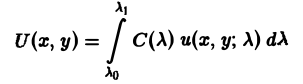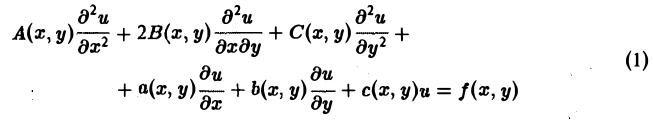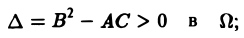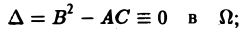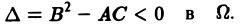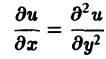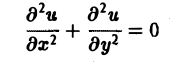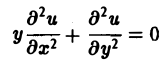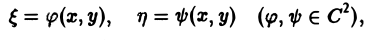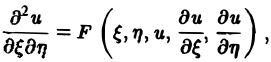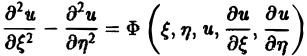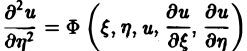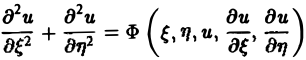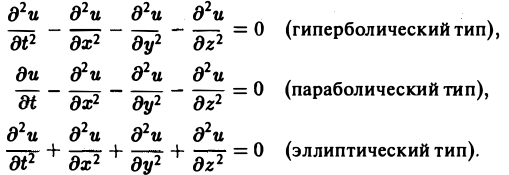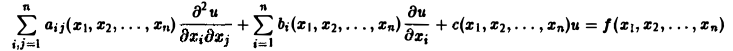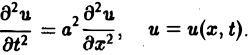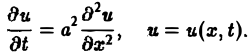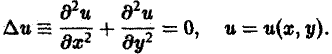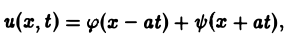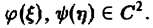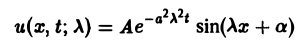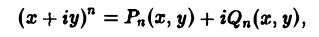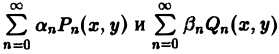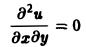Дифференциальные уравнения в частных производных физики

Методы решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

5.2. Методы решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

5.2.1. Обзор методов решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

Дифференциальные уравнения в частных производных классифицируют либо в зависимости от их математической природы — эллиптические, параболические и т. п. — либо в зависимости от физического смысла решаемых с их помощью задач — уравнение диффузии, волновое уравнение и т. п. Приведем классификацию наиболее часто встречающихся простейших уравнений в частных производных и области их использования.

Примеры задач, в которых встречается уравнение

Установившееся течение жидкости. Стационарные тепловые поля.

Теплопередача с внутренними источниками тепла.

Распространение звуковых волн.

Здесь: ; D 2f=

В настоящее время можно выделить три основных подхода к решению задач математической физики. Прежде всего это широкий спектр математических методов, известных под названием взвешенных невязок (рисунок ниже).

К другому классу относят различные сеточные или конечно-разностные методы, получившие широкое распространение вследствие простоты и наглядности формулировки и, наконец, интенсивно развивающиеся в последнее время вероятностные методы.

Широкому распространению некоторых модификаций этих методов способствовало прежде всего появление ЭВМ, а также достаточно степень алгоритмизации, разрешаемая структурой этих методов.

5.2.2. Метод конечных разностей для уравнений в частных производных.

Также как и при решении методом конечных разностей обыкновенных дифференциальных уравнений в основе решения уравнений в частных производных тем же методом лежит конечно-разностная аппроксимация производных. В области изменения независимых переменных уравнения L(f)=0 вводится сетка с достаточно малым шагом h. Отсюда МКР, применяемый для решения двумерных задач, часто называют методом сеток. Алгебраическое (или трансцендентное) уравнение Lh(f)=0 ,определенное в узлах сетки путем замены производных их конечно-разностными соотношениями и называемое сеточным или разностным уравнением, должно обеспечивать при неограниченном измельчении сетки при h®0 для любой достаточно гладкой функции Lh(f) ® L(f). При этом величина | Lh(f) — L(f)|. называется локальной погрешностью или погрешностью аппроксимации (дискретизации). Погрешность аппроксимации легко определяется при помощи разложений в окрестности данного узла сетки достаточно гладкой функции в соответствующие ряды Тейлора.

В основе решения уравнения в частных производных методом конечных разностей лежит конечно-разностная схема аппроксимации производных, которая во многом напоминает описанную ранее процедуру для обыкновенных дифференциальных уравнений.

Аппроксимация осуществляется в три этапа:

Сначала в области решения вводят равномерную сетку ²узловых точек², соответствующую характеру задачи и граничным условиям. Затем решаемое уравнение в частных производных записывают в наиболее удобной системе координат и, представляя производные в конечно-разностной форме, приводят его к виду разностного уравнения.

Полученное разностное уравнение используют в дальнейшем для описания функциональной связи между соседними узлами сетки. Разностное уравнение записывают для всех узлов сетки и получают в результате систему n уравнений с n неизвестными. На последнем этапе полученную систему n уравнений с n неизвестными решают одним из численных методов. На первый взгляд эта процедура, состоящая из трех этапов, может показаться простой и прямо ведущей к решению, однако это не так — широкое разнообразие типов и размеров сеток, видов уравнений, возможных конечно-разностных аппроксимаций и методов решения получаемых систем уравнений делают задачу численного решения уравнений в частных производных исключительно многогранным исследованием.

Наиболее часто используются следующие виды сеток:

а) прямоугольная; б) полярная; в) треугольная; г) скошенная.

Запишем несколько формул, выражающих производные функции двух переменных в конечных разностях, для сетки с квадратной ячейкой и — шагом сетки (см. рисунок):

Получим также формулу для смешанной производной:

Можно выразить и лапсиан:

Информацию о коэффициентах при значениях функции в выражениях для конечно-разностных аналогов производных удобно представлять с помощью вычислительных шаблонов, являющихся диаграммами, показывающими, какой вклад вносят узлы сетки в рассматриваемую производную. Ниже приводятся вычислительные шаблоны для наиболее часто встречающихся производных.

Аналогично , , и т. д., например:

Напомним, что D 2f=

Все приведенные вычислительные шаблоны имеют погрешность порядка h .

Следует отметить, что можно построить и более точные (имеющие меньшую погрешность) вычислительные шаблоны, если включить в рассмотрение дополнительные узлы. В основе всех построенных до сих пор вычислительных шаблонов лежит центрально — разностная аппроксимация. Иногда, чтобы свести к минимуму распространение ошибок, пользуются левыми и правыми разностями.

Вычислительными шаблонами следует пользоваться с осторожностью, так как построенное с их помощью разностное уравнение, аппроксимирующее дифференциальное уравнение в частных производных, при счете может оказаться неустойчивым. Разностная схема считается неустойчивой, если погрешность, каково бы ни было ее происхождение, с течением времени не убывает.

Границы неправильной формы.

Нередко приходится иметь дело с областями неправильной формы. Хотя границы таких областей нельзя точно задать с помощью какой-либо одной из указанных сеток, существуют специальные методы, с помощью которых можно так модифицировать стандартные сетки, что они позволяют описать границу сложной конфигурации.

Вычислительные шаблоны для конкретного дифференциального уравнения в частных производных можно видоизменить так, чтобы учесть неправильную форму границ рассматриваемой области. Для этого, записывая производные в центрально-разностной форме, следует учесть вклад узлов, лежащих на границе области. В качестве примера рассмотрим вычислительный шаблон уравнения Лапласа в области ограниченной произвольной кривой.

Вторые частные производные для узлов, лежащих на границе области, можно записать в виде.

;

Сложив две производные, получим D f. После ряда преобразований найдем:

Соответствующий вычислительный шаблон представлен ниже.

Применив вычислительный шаблон к каждому из n узлов сетки, получим систему n уравнений, которая может быть линейной, если исходное уравнение имеет соответствующую структуру. В этом случае придется решать систему уравнений вида:

X=

Обычно матрица коэффициентов оказывается ²разреженной² (содержит много нулевых элементов), так как в большей части вычислительных схем используется лишь несколько соседних узлов, а не все узлы сетки.

Методы решения таких уравнений делятся на прямые и итерационные. Прямые методы позволяют получить точное решение, выполнив конечное число операций. Примером прямого метода может служить правило Крамера для решения совместных линейных алгебраических уравнений. Обычно для больших систем уравнений прямые методы неэффективны, так как при их применении требуется выполнение огромного объема вычислений и очень большой объем памяти ЭВМ. Поэтому чаще всего пользуются итерационными методами. Сущность итерационных методов заключается в многократном повторении одного и того же простого алгоритма, который дает результат, постоянно приближающийся к точному решению. Итерации начинаются с задания начального приближенного решения. Затем начальные значения переменных в узлах сетки последовательно меняются, пока не достигается заданная точность решения. Быстрота сходимости итерационного метода сильно зависит от степени точности начальной аппроксимации. Поэтому интуиция инженера может оказать большое внимание на эффективность вычислительного процесса. Итерационные методы подразделяются на точечные и блочные. В первом случае алгоритм используется для модификации приближенного решения в одном узле сетки, покрывающей область. Во втором случае решение модифицируется сразу в группе узлов сетки. Наиболее часто применяемые точечные методы: Метод Якоби, метод последовательных смещений, метод последовательной верхней релаксации. Эти методы знакомы по курсу ²Численные методы и оптимизация², поэтому, здесь они рассматриваться не будут.

Рассмотрим пример решения дифференциального уравнения в частных производных.

Пример 3. Определить прогибы прямоугольной шарнирно-опертой пластины при распределенной нагрузке, направленной перпендикулярно плоскости пластины.

Будем рассматривать изотропную пластину постоянной жесткости. Разрешающее уравнение такой пластины имеет вид:

где w = w (x, y) — функция прогибов, q =q (x, y) — поперечная распределенная нагрузка,

Здесь D = — цилиндрическая жесткость

Разделим пластину в каждом направлении на четыре части:

Точки 1 — 9 — внутренние узловые. Точки III — IX граничные точки.

Используем формулы (или шаблоны):

;

;

Точка 1.

+

Последние два условия, записанные в конечных разностях, дают:

; ;

Таким образом, алгебраическое уравнение, соответствующее первой узловой точке, принимает вид:

и уравнение, соответствующе 2-ой узловой точке принимает вид:

Для упрощения решения положим q=q0=const, Dx=Dy=a/4, a=b, т. е. имеем квадратную пластину при равномерном давлении и сетку с квадратной клеткой. Тогда из симметрии следует

w1=w3=w7=w9; w2=w4=w6=w9. Тогда разрешающая система алгебраических уравнений с учётом вида уравнений, построенных для узловых точек 1, 2 и 5 будет иметь вид:

— 16w2 + 2w5 = 20w1 qa4 / 256 D

-16w1 + 28w2 — 8w5 = qa4 / 256 D (5.3.22)

8w1 —32w2 + 20w5 = qa4 / 256 D

Из решения этих уравнений имеем:

Максимальный прогиб (в точке 5) :;

Точное решение:

Ознакомившись с МКР, нельзя не отметить исключительную простоту и ясность его принципов. Поэтому может показаться удивительным, что после относительно короткого периода популярности и бурного развития ныне этот метод используется все реже.

Назовем три главные причины вытеснения этого метода из практики.

1. Решение систем вида, аналогичному системе из трёх уравнений (5.3.22) рассмотренного примера выполняется очень быстро. Сложность кроется не в решении, а в составлении таких систем уравнений. В рассмотренных выше примерах мы, в целях упрощения, ограничивались прямоугольной областью. В большинстве практически важных задач область определения решения имеет более сложную форму (см рисунок).

В этом случае точки, в которых заданы граничные условия не всегда попадают на узловые точки равномерной сетки. Об этом мы говорили раньше. Кроме того, как мы убедились, при рассмотрении конкретных задач на границе могут задаваться не только значения некоторой функции, но и ее производные, или даже их комбинации. В результате помимо однотипных аккуратных уравнений типа (5.3.21) (5.3.22) в систему вклиниваются уравнения совсем другого вида. В этом случае матрица системы уже имеет не такой простой вид и имеет ряд нестандартных строк..

Таким образом, первая причина первая – сложность задания граничных условий.

2. Очень часто решение дифференциального уравнения оказывается быстро меняющимся на одних участках и гладким на других. Таково, например, решение задачи о краевом эффекте. Так в топливном баке, изображенном на рисунке, в зоне стыка цилиндрической обечайки шпангоута и сферического днища возникают изгибные деформации, которые быстро затухают по мере удаления от места стыка. Для того, чтобы численное решение на участке быстрого изменения функции было достаточно точным, шаг конечно-разностной сетки должен быть очень малым. В то же время на удалении от зоны краевого эффекта в использовании такого же мелкого шага нет никакой необходимости. Возникают два варианта решения проблемы: 1) во всей области задать малый шаг и получить систему с огромным количеством неизвестных; 2) использовать переменный шаг и значительно усложнить выражения конечно-разностных аппроксимаций производных.

Поэтому причина вторая – сложно обеспечить различную точность решения для различных участков области.

3. При расчете прочности какой-либо реальной конструкции, оказывается, что для различных ее частей необходимо использовать различные дифференциальные уравнения. Так, например, для крыла работа поясов лонжеронов хорошо описывается с помощью уравнений растяжения-сжатия стержня; для стенок лонжеронов и нервюр хорошей математической моделью являются уравнения плоской задачи теории упругости; для обшивки подходит безмоментная теория оболочек. Между тем каждая из этих теорий описывается различными дифференциальными уравнениями. Значит, конечно-разностные аппроксимации этих уравнений будут различными. Кроме того, основные неизвестные в этих системах дифференциальных уравнений могут оказаться различными по физическому смыслу. Следовательно, возникает проблема увязки решений друг с другом. Таким образом, третья причина вытеснения МКР – сложности, возникающие при объединении различных математических моделей в единую расчетную схему.

Конечно, все эти три проблемы не являются неразрешимыми. В период примерно тридцатилетнего периода активного использования разностных методов разработаны способы решения многих задач математической физики, в том числе и механики деформируемого твёрдого тела. Дело, однако, в том, что родившийся в 1956 году метод конечных элементов (МКЭ) очень просто решает большинство из перечисленных проблем

Итак, с середины 50-х годов прошлого столетия интенсивно развивающийся метод конечных элементов (МКЭ), впервые применённый для описания сплошных сред и с тех пор завоевавший известность исключительно полезного инженерного метода, стал широко применяеться в гидродинамике, аэродинамике, теории поля, при расчете сложных напряженных состояний и в других областях. Хотя метод конечных элементов применяется для решения тех же задач, что и метод конечных разностей, основаны они на разных идеях.

В методе конечных разностей производится аппроксимация производных, входящих в дифференциальные уравнения.

В методе конечных элементов аппроксимируется функция в объёме (площади, протяжении) конечного элемента.

Для этого физическая задача заменяется кусочно-гладкой моделью, отдельные части которой рассматриваются как реальные физические тела, работающие каждый по своему (или одинаковому) закону. Т. е. работа сложной системы заменяется совместной работой элементов её образующих. Это позволяет инженеру использовать свое интуитивное понимание задачи.

Метод конечных элементов значительно более сложен для понимания, чем МКР, но обладает огромными преимуществами по сравнению с МКР, главное из которых заключается в возможности построения на его основе программ широкого назначения для решения широкого круга задач математической физики. Поэтому его рассмотрению в дальнейшем будет уделено самое пристальное внимание, а настоящий раздел завершим примерными рекомендациями по решению дифференциальных уравнений в частных производных.

5.3.2. Общие рекомендации по решению дифференциальных уравнений в частных производных.

Поскольку каждому уравнению в частных производных присущи свои особенности, а граничные условия делают каждую задачу непохожей на другие, то практически невозможно сформулировать общие рекомендации, которые были бы полезны при решении таких уравнений. Однако во всех случаях полезно иметь в виду следующие правила:

1. Сначала следует выяснить, какова должна быть точность искомого решения. Если она высока, то для решения данного дифференциального уравнения может потребоваться весьма мелкая сетка или разбиение тела на очень малые элементы.

2. Затем надо внимательно изучить форму области, в которой отыскивается решение. Учесть симметрию и т. д.

3. Следует тщательно выбирать начальные значения переменных. При использовании итерационных методов скорость сходимости прямо зависит от близости исходных данных к решению.

Если хорошее исходное приближение задать не удается, то может оказаться полезным разделить решение задачи на два и более этапов. На первом этапе с помощью весьма грубой сетки или разбиения на очень крупные элементы получают хорошее исходное приближение, а затем уже ищут точное решение на гораздо более мелкой сетке или разбивая тело на мелкие элементы.

4. Следует выбрать метод, более всего подходящий для решения данной задачи.

Дифференциальные уравнения в частных производных физики

Адамар Ж. Задача Коши для линейных уравнений с частными производными гиперболического типа. М.: Наука, 1978 (pdf)

Араманович И.Г., Левин В.И. Уравнения математической физики (2-е изд.). М.: Наука, 1969 (pdf)

Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. М.: Наука, 1972 (pdf)

Бабич В.М., Кирпичникова Н.Я. Метод пограничного слоя в задачах дифракции. Л.: ЛГУ, 1974 (pdf)

Бакельман И.Я. Геометрические методы решения эллиптических уравнений. М.: Наука, 1965 (pdf)

Бергман С. Интегральные операторы в теории линейных уравнений с частными производными. М.: Мир, 1964 (pdf)

Бернштейн С.П. Аналитическая природа решений дифференциальных уравнений эллиптического типа. Харьков: ХГУ, 1956 (pdf)

Беpc Л., Джон Ф., Шехтер М. Уравнения с частными производными. М.: Мир, 1966 (pdf)

Брело М. О топологиях и границах в теории потенциала. М.: Мир, 1974 (pdf)

Брело М. Основы классической теории потенциала. М.: Мир, 1964 (pdf)

Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике (3-е изд.). М.: Наука, 1979 (pdf)

Векуа ИН. Новые методы решения эллиптических уравнений. М.-Л. ГИТТЛ, 1948 (pdf)

Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975 (pdf)

Гельфанд И.М., Шилов Г.Е. Пространства основных и обобщенных функций (Обобщенные функции, выпуск 2). М.: Физматлит, 1958 (pdf)

Годунов С.К. Уравнения математической физики (2-е изд. ). М.: Наука 1979 (pdf)

Годунов С.К., Золотарева Е.В. Сборник задач по уравнениям математической физики. Новосибирск: Наука, 1974 (pdf)

Гординг Л. Задача Коши для гиперболических уравнений. М.: ИЛ, 1961 (pdf)

Гурса Э. Курс математического анализа, том 3, часть 1. Бесконечно близкие интегралы. Уравнения с частными производными. М.-Л.: ГТТИ, 1933 (pdf)

Гюнтер Н.М. Интегрирование уравнений в частных производных первого порядка. Л.-М.: ОНТИ, 1934 (pdf)

Гюнтер Н. Теория потенциала и ее применение к основным задачам математической физики. М.: ГИТТЛ, 1953 (pdf)

Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. М.: Наука, 1967 (pdf)

Егоров Д. Интегрирование дифференциальных уравнений (3-е изд.). М.: Печатня Яковлева, 1913 (pdf)

Егоров Д.Ф. Уравнения с частными производными 2-го порядка с двумя независимыми переменными. М.: МГУ, 1899 (pdf)

Егоров Ю.В., Шубин М.А., Комеч А.И. Дифференциальные уравнения с частными производными — 2 (серия «Современные проблемы математики», том 31). М.: ВИНИТИ, 1988 (pdf)

Зайцев Г.А. Алгебраические проблемы математический и теоретической физики. М.: Наука, 1974 (pdf)

Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: от маятника до турбулентности и хаоса. М.: Наука, 1988 (pdf)

Зельдович Я.Б., Мышкис А.Д. Элементы математической физики. Среда из невзаимодействующих частиц. М.: Наука, 1973 (pdf)

Зоммерфельд А. Дифференциальные уравнения в частных производных физики. М.: ИЛ, 1950 (pdf)

Ибрагимов Н.Х. Азбука группового анализа. М.: Знание, 1989 (pdf)

Ибрагимов Н.Х. Группы преобразований в математической физике. М.: Наука, 1983 (pdf)

Имшенецкий В.Г. Интегрирование дифференциальных уравнений с частными производными 1-го и 2-го порядков. М.: Изд. Моск. мат. общества, 1916 (pdf)

Йон Ф. Плоские волны и сферические средние в применении к дифференциальным уравнениям с частными производными. М.: ИЛ, 1958 (pdf)

Калоджеро Ф., Дигасперис А. Спектральные преобразования и солитоны. Методы решения и исследования нелинейных эволюционных уравнений. М.: Мир, 1985 (pdf)

Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966 (pdf)

Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука, 1973 (pdf)

Кирхгоф Г. Механика. Лекции по математической физике. М.: АН СССР, 1962 (pdf)

Коркин А.Н. Сочинения, том 1. СПб.: Императорская Академия Наук, 1911 (pdf)

Коллатц Л. Задачи на собственные значения (с техническими приложениями). М.: Наука, 1968 (pdf)

Коул Дж. Методы возмущений в прикладной математике. М.: Мир, 1972 (pdf)

Кошляков Н.С. Глинер Э.Б. Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970 (pdf)

Курант Р. Уравнения с частными производными. М.: Мир, 1964 (pdf)

Курант Р., Гильберт Д. Методы математической физики. Том 1. М.-Л.: ГТТИ, 1933 (pdf)

Курант Р., Гильберт Д. Методы математической физики. Том 2. М.-Л.: ГТТИ, 1945 (pdf)

Куренский М.К. Дифференциальные уравнения. Книга 2. Дифференциальные уравнения с частными производными. Л.: Артиллерийская академия, 1934 (pdf)

Лаврентьев М.А. Вариационный метод в краевых задачах для систем уравнений эллиптического типа. М.: АН СССР, 1962 (pdf)

Ладыженская О.А. Краевые задачи математической физики. М.: Наука, 1973 (pdf)

Ладыженская О.А., Солонников В.А., Уралыдева Н.Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967 (pdf)

Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллиптического типа (2-е изд.). М.: Наука, 1973 (pdf)

Лакс П., Филлипс Р. Теория рассеяния. М.: Мир, 1971 (pdf)

Ландис E.M. Уравнения второго порядка эллиптического и параболического типов. М.: Наука, 1971 (pdf)

Лаптев Г.И., Лаптев Г.Г. Уравнения математической физики. М.: 2003 (pdf)

Лионс Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972 (pdf)

Лионс Ж.-Л. Оптимальное управление системами, описываемыми уравнениями в частных производных. М.: Мир, 1972 (pdf)

Маделунг Э. Математический аппарат физики: Справочное руководство. М.: Наука, 1968 (pdf)

Маслов В.П. Асимптотические методы и теория возмущений. М.: Наука, 1988 (pdf)

Маслов В.П., Федорюк М.В. Квазиклассическое приближение для уравнений квантовой механики. М.: Наука, 1976 (pdf)

Марченко В.А., Хруслов Е.Я. Краевые задачи в областях с мелкозернистой границей. Киев: Наук. думка, 1974 (pdf)

Мизохата С. Теория уравнений с частными производными. М.: Мир, 1977 (pdf)

Миллер У. (мл.). Симметрия и разделение переменных. М.: Мир, 1981 (pdf)

Миранда К. Уравнения с частными производными эллиптического типа. М.: ИЛ, 1957 (pdf)

Михайлов В.П. Дифференциальные уравнения в частных производных.М.: Наука, 1976 (pdf)

Михлин С.Г. Курс математической физики. М.: Наука, 1968 (pdf)

Михлин С.Г. Линейные уравнения в частных производных. М.: Высшая школа, 1977 (pdf)

Михлин С.Г. (ред.). Линейные уравнения математической физики. М.: Наука, 1964 (pdf)

Морс Ф.М., Фешбах Г. Методы теоретической физики. Том 1. М.: ИЛ, 1958 (pdf)

Морс Ф.М., Фешбах Г. Методы теоретической физики. Том 2. М.: ИЛ, 1960 (djvu)

Нагумо М. Лекции по современной теории уравнений в частных производных. М.: Мир, 1967 (pdf)

Назимов П.С. Об интегрировании дифференциальных уравнений. М.: МГУ, 1880 (pdf)

Нобл Б. Применение метода Винера — Хопфа для решения дифференциальных уравнений с частными производными. М.: ИЛ, 1962 (pdf)

Оганесян Л.А., Руховец Л.А. Вариационно-разностные методы решения эллиптических уравнений, Ереван: АН АрмССР, 1979 (pdf)

Олейник О.А., Иосифьян Г.А., Шамаев А.С. Математические задачи теории сильно неоднородных упругих сред. М.: Изд-во МГУ, 1990 (pdf)

Паламодов В.П. Линейные дифференциальные операторы с постоянными коэффициентами. М.: Наука, 1967 (pdf)

Петровский И.Г. Лекции об уравнениях с частными производными (3-е изд.). М.: Наука, 1961 (pdf)

Расулов М.Л. Метод контурного интеграла и его применение к исследованию задач для дифференциальных уравнений. М.: Наука, 1964 (pdf)

Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике (2-е изд.) М.: Наука, 1978 (pdf)

Салтыков Н.Н. Исследования по теории уравнений с частными производными первого порядка одной неизвестной функции. Харьков, 1904 (pdf)

Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971 (pdf)

Синцов Д.М. Теория коннексов в пространстве в связи с теорией дифференциальных уравнений в частных производных первого порядка. Казань: КГУ, 1894 (pdf)

Смирнов М.М. Дифференциальные уравнения в частных производных второго порядка. М.: Наука, 1964 (pdf)

Смирнов М.М. Задачи по уравнениям математической физики (6-е изд.). М.: Наука, 1973 (djvu)

Смирнов М.М. Уравнения смешанного типа. М.: Наука, 1970 (pdf)

Соболев С.Л. Уравнения математической физики (4-е изд.). М.: Наука, 1966 (pdf)

Степанов В.В. Курс дифференциальных уравнений (8-е изд.). М.: ГИФМЛ, 1959 (pdf)

Тихонов А.Н., Самарский А.А. Уравнения математической физики (5-е изд.). М.: Наука, 1977 (djvu)

Трев Ж. Лекции по линейным уравнениям в частных производных с постоянными коэффициентами. М.: Мир, 1965 (pdf)

Фещенко С.Ф., Шкиль Н.И., Николенко Л.Д. Асимптотические методы в теории линейных дифференциальных уравнений. Киев: Наукова думка, 1966 (pdf)

Фущич В.И., Никитин А.Г. Симметрия уравнений квантовой механики. М.: Наука, 1990 (pdf)

Хёрмандер Л. К теории общих дифференциальных операторов в частных производных. М.: ИЛ, 1959 (pdf)

Ховратович Д.В. Уравнения математической физики, МГУ (pdf)

Шилов Г.Е. Математический анализ. Второй специальный курс. М.: Физматлит, 1965 (pdf)

Шишмарев И.А. Введение в теорию эллиптических уравнений. М.: МГУ, 1979 (pdf)

Контакты

Адрес: пр. Ленина 31 Город: Якутск, 677027 Эл. почта: ikfia@ysn.ru Тел.: +7 (4112) 390-400 Факс: +7 (4112) 390-450 Охрана тел.: +7 (4112) 390-489 Охрана тел.: +7 (4112) 335-176

Новости

XIV конференция научной молодежи «Актуальные вопросы космофизики». Итоги конференции

Институт космофизических исследований и аэрономии им. Ю.Г. Шафера СО РАН в рамках чтений, посвященных 100-летию со дня рождения организатора аэрономического.

XIV конференция научной молодежи «Актуальные вопросы космофизики». Второе информационное сообщение

Институт космофизических исследований и аэрономии им. Ю.Г. Шафера СО РАН в рамках чтений, посвященных 100-летию со дня рождения организатора аэрономического.

Приказ ИКФИА №13-к от 04.02.2022 о деятельности Института в условиях недопущения дальнейшего распространения новой коронавирусной инфекции

3 января 2022 г. исполнилось 100-лет со дня рождения к.ф.-м.н. Самсонова Владимира Парфеньевича – организатора аэрономического направления и исследований полярных сияний в Институте.

В честь юбилея 11 февраля 2022 г. в режиме видеоконференции планируется проведение научных чтений, совмещенных с празднованием Дня науки и.

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

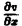
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 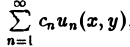, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 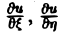и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 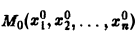и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 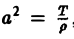где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 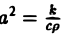где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

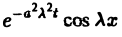
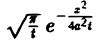
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института