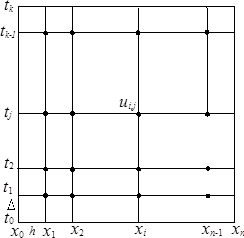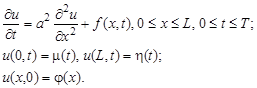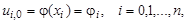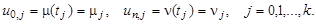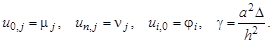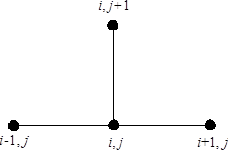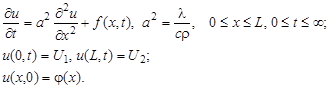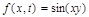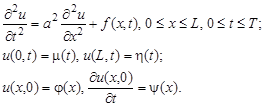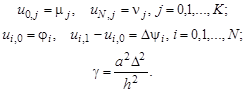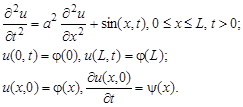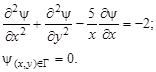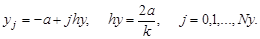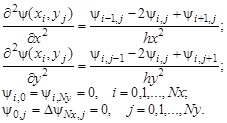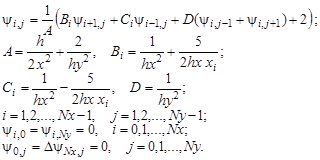Дифференциальные уравнения в частных производных метод сеток

Дифференциальные уравнения в частных производных метод сеток

3. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

3.2. Понятие о методе конечных разностей

Для численного решения дифференциального уравнения с частными производными обычно применяют метод конечных разностей или метод сеток. Он позволяет свести решение дифференциального уравнения к решению системы алгебраических уравнений.

Метод сеток состоит в следующем:

1) область непрерывного изменения аргументов заменяют областью их дискретного изменения;

2) непрерывные производные заменяют разностными отношениями;

3) для краевых и начальных условий записывают разностный аналог.

Таким образом, сетка представляет собой множество точек. Отдельные точки называются узлами сетки. Функция, определяемая в узлах сетки, называется сеточной функцией.

Рассмотрим примеры сеток.

1. Равномерная сетка на отрезке [а, в ].

Разобьем отрезок на n равных частей и получим систему точек x ₀ , x ₁ , x ₂ ,…, x _n такую что:

Непрерывная функция y ( x ) заменяется сеточной функцией y _h ( x _i ), определяемой в узлах сетки и зависимой от шага h как от параметра.

2. Равномерная сетка на плоскости.

Разобьем отрезок [0, x _max ] на n равных частей и получим систему точек x ₀ , x ₁ ,…, x _n , где h ₁ = x _max / n .Отрезок [0, y _max ] разделим на m равных частей точками y ₀ , y ₁ ,…, y _m с шагом h ₂ = y_max / m . Через точки x _i проведем линии, параллельные оси x . Искомая функция U ( x , y ) заменяется сеточной функцией и зависят от параметров h ₁ и h ₂ .

3.2.1. Конечные разности.

-правая разностная производная,

— левая разностная производная;

— центральная разностная производная.

Левая и правая конечные разности аппроксимируют производную с первым порядком точности, а центральная разностная производная – со вторым порядком точности.

Конечно – разностная производная второго порядка имеет вид:

При замене частных производных разностными отношениями применяется аналогичный подход:

Численные методы решения дифференциальных уравнений в частных производных

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных

Одним из наиболее распространенных численных методов решения уравнений в частных производных является метод сеток. В методе сеток область Ω, в которой необходимо найти решение уравнения, разобьем прямыми, параллельными осям и , на прямоугольные области (рис.1.1), где

,

.

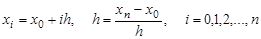
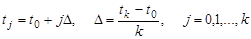
Точки, которые лежат на границе области Ω, называются внешними, остальные точки – внутренними. Совокупность всех точек называется сеткой, величины h и Δ – шагами сетки по хи t соответственно.

Рис.1.1. Сетка 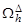для области Ω

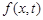
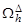
Идея метода сеток состоит в том, что вместо любой непрерывной функции будем рассматривать дискретную функцию , которая определена в узлах сетки , вместо производных функции будем рассматривать их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получим систему алгебраических уравнений. Чем меньше величины h иΔ, тем точнее получаемые алгебраические уравнения моделируют исходное дифференциальное уравнение в частных производных. В этом и последующих подразделах этой главы будет рассмотрен метод сеток для каждого из трех типов уравнений и его реализация в MATLAB. Знакомство с численными методами решения дифференциальных уравнений в частных производных начнем с разностных схем решения параболических уравнений.

Разностные схемы решения параболических уравнений будем рассматривать на примере следующего одномерного уравнения:

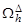
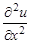
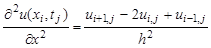
Построим сетку (см. рис.1.1). Для получения сеточного уравнения заменим производную приближенной разностной формулой:

.

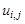
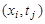
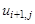
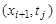
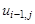
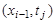
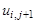
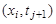
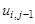
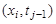
В этой и последующих формулах – значение функции u в точке , – в точке , – в точке , – в точке , – в точке .

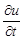
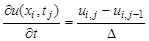
Для замены можно воспользоваться одной из приближенных разностных формул

;

.

Кроме того, заменим начальные и граничные условия их разностной аппроксимацией:

Заменив частные производные в задаче соответствующими разностными соотношениями, получим следующую вычислительную схему для расчета значений функции и в узлах сетки :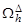

;

Это явная двухслойная разностная схема (рис.1.2).

Рис.1.2. Шаблон явной двухслойной разностной схемы

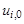
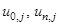
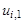
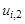
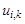
Учитывая, что на нулевом слое (при i = 0)все значения (как, впрочем, и ) известны, можно сначала явно рассчитать значения , затем и так до .Для устойчивости разностной схемы значения шагов по t и х должны удовлетворять следующему условию:

.

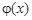
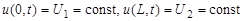
Пример. Решить параболическое уравнение, описывающее распределение температуры в стержне длиной L,начальная температура стержня задается произвольной функцией . Температуры концов стержня равны .

Здесь а 2 – коэффициент температуропроводности; 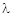– коэффициент теплопроводности материала стержня; с – удельная теплоемкость; – плотность массы.

Подпрограмма решения задачи с помощью явной разностной схемы в MATLAB:

//Правая часть дифференциального уравнения

//Условие на левой границе

//Условие на правой границе

//Функция решения параболического уравнения методом сеток с помощью явной разностной схемы. N — количество участков разбиения интервала по х (0,1_); К – количество участков разбиения интервала по t (0,Т); а — коэффициент температуропроводности,

// Функция возвращает матрицу решений u вектора х, t

// Вычисляем шаг по х

// Вычисляем шаг по t

// Формируем массив х и первый столбец матрицы решений u

// из начального условия

//Формируем массив t, первую и последнюю строку матрицы решений u из граничных условий

gam = a ^ 2*delta/h ^ 2;

// Формируем матрицу решений u

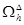
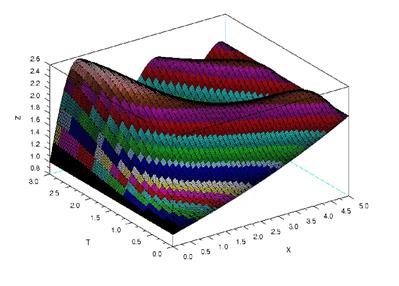
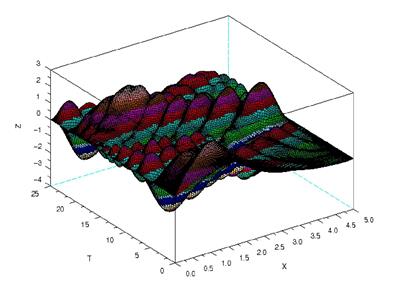
Входными данными подпрограммы parabol решения задачи являются: N – количество интервалов, на которые разбивается отрезок (О, L); К – количество интервалов, на которые разбивается отрезок (О, Т); L – длина стержня, Т – интервал времени, а – параметр дифференциального уравнения. Функция возвращает три параметра: решение – сеточная функция u, определенная на сетке , массивы x и t.

График решения данной задачи изображен на рис.1.3.

Рис.1.3. График решения параболического уравнения при

1.4.2. Использование метода сеток для решения гиперболических уравнений

Решение гиперболических уравнений также можно осуществить с помощью разностных схем. Разностные схемы решения одномерного гиперболического уравнения рассмотрим на примере следующего уравнения:

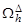
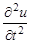
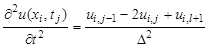
Построим сетку , в которой будем искать решение уравнения. Производную заменим соотношением:

,

остальные производные такие же, как и в предыдущем подразделе.

Получим следующую явную разностную схему решения уравнения:

Она устойчива при 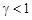и по аналогии с разностной схемой (см. подразд. 1.4.1) может быть легко запрограммирована в MATLAB.

В качестве примера рассмотрим следующую задачу.

Пример. Решить начально-граничную задачу:

Ниже представлена функция giperbol решения данного уравнения, а на рис.1.4 – график полученного решения. Параметры функциианалогичны рассмотренным ранее, т.е. в подпрограмме решения параболического уравнения.

//Функция решения гиперболического уравнения с помощью явной разностной схемы. Входные данные: N — количество участков разбиения интервала (0,L); K — количество участков разбиения интервала (0,T); a — коэффициент теплопроводности; u — матрица решений в узлах сетки; массив x; массив t,

// Вычисляем шаг по х и по t

//Формируем массив x, первый и второй столбцы матрицы решений u из начального условия

//Формируем массив t, первую и последнюю строки матрицы решений u из граничных условий

//Формируем первую и последнюю строки матрицы решений u из граничных условий

//Формируем матрицу решений u

Рис.1.4. График решения гиперболического уравнения

1.4.3. Использование метода сеток для решения эллиптических уравнений

Разностные схемы решения одномерного эллиптического уравнения рассмотрим на следующем примере.

Пример. Рассмотрим разностную схему для эллиптического уравнения в прямоугольной области 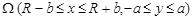с граничными условиями Дирихле на границе Г:

Проведем в области Ω прямые, параллельные осям и , где ;

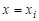
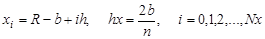
Для построения разностного уравнения заменим частные производные и граничные условия следующими соотношениями:

Преобразуем данную эллиптическую краевую задачу к следующей системе разностных уравнений:

Эту систему можно решать итерационными методами (например, методом Зейделя). В случае медленной сходимости итерационных процессов при решении сеточных уравнений, получаемых при аппроксимации гиперболических и эллиптических задач, можно попробовать заменить метод Зейделя градиентными методами (или методами релаксации). Ниже представлено решение эллиптического уравнения сеточным методом, а на рис.1.5 график полученного решения.

Рис.1.5. График решения эллиптического уравнения

// Функция ellip решения задачи

// Входные данные:R, a, b — значения, определяющие область решения задачи; Nx — количество участков разбиения интервала(R-b,R+b); Ny — количество участков разбиения интервала(-a,a); eps — точность решения уравнения методом Зейделя.

// psi — матрица решений в узлах сетки, массив x, массив y, k — количество итераций при решении разностного уравнения

// Вычисляем шаг по y и по x

// Формируем массив x, первый и последний столбцы матрицы решений psi из граничного условия

// Формируем массив y, первую и последнюю строки матрицы решений psi из граничного условия

// Вычисляем коэффициенты разностного уравнения

//Решение разностного уравнения методом Зейделя

Методы решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

5.2. Методы решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

5.2.1. Обзор методов решения задач математической физики, описываемых дифференциальными уравнениями в частных производных

Дифференциальные уравнения в частных производных классифицируют либо в зависимости от их математической природы — эллиптические, параболические и т. п. — либо в зависимости от физического смысла решаемых с их помощью задач — уравнение диффузии, волновое уравнение и т. п. Приведем классификацию наиболее часто встречающихся простейших уравнений в частных производных и области их использования.

Примеры задач, в которых встречается уравнение

Установившееся течение жидкости. Стационарные тепловые поля.

Теплопередача с внутренними источниками тепла.

Распространение звуковых волн.

Здесь: ; D 2f=

В настоящее время можно выделить три основных подхода к решению задач математической физики. Прежде всего это широкий спектр математических методов, известных под названием взвешенных невязок (рисунок ниже).

К другому классу относят различные сеточные или конечно-разностные методы, получившие широкое распространение вследствие простоты и наглядности формулировки и, наконец, интенсивно развивающиеся в последнее время вероятностные методы.

Широкому распространению некоторых модификаций этих методов способствовало прежде всего появление ЭВМ, а также достаточно степень алгоритмизации, разрешаемая структурой этих методов.

5.2.2. Метод конечных разностей для уравнений в частных производных.

Также как и при решении методом конечных разностей обыкновенных дифференциальных уравнений в основе решения уравнений в частных производных тем же методом лежит конечно-разностная аппроксимация производных. В области изменения независимых переменных уравнения L(f)=0 вводится сетка с достаточно малым шагом h. Отсюда МКР, применяемый для решения двумерных задач, часто называют методом сеток. Алгебраическое (или трансцендентное) уравнение Lh(f)=0 ,определенное в узлах сетки путем замены производных их конечно-разностными соотношениями и называемое сеточным или разностным уравнением, должно обеспечивать при неограниченном измельчении сетки при h®0 для любой достаточно гладкой функции Lh(f) ® L(f). При этом величина | Lh(f) — L(f)|. называется локальной погрешностью или погрешностью аппроксимации (дискретизации). Погрешность аппроксимации легко определяется при помощи разложений в окрестности данного узла сетки достаточно гладкой функции в соответствующие ряды Тейлора.

В основе решения уравнения в частных производных методом конечных разностей лежит конечно-разностная схема аппроксимации производных, которая во многом напоминает описанную ранее процедуру для обыкновенных дифференциальных уравнений.

Аппроксимация осуществляется в три этапа:

Сначала в области решения вводят равномерную сетку ²узловых точек², соответствующую характеру задачи и граничным условиям. Затем решаемое уравнение в частных производных записывают в наиболее удобной системе координат и, представляя производные в конечно-разностной форме, приводят его к виду разностного уравнения.

Полученное разностное уравнение используют в дальнейшем для описания функциональной связи между соседними узлами сетки. Разностное уравнение записывают для всех узлов сетки и получают в результате систему n уравнений с n неизвестными. На последнем этапе полученную систему n уравнений с n неизвестными решают одним из численных методов. На первый взгляд эта процедура, состоящая из трех этапов, может показаться простой и прямо ведущей к решению, однако это не так — широкое разнообразие типов и размеров сеток, видов уравнений, возможных конечно-разностных аппроксимаций и методов решения получаемых систем уравнений делают задачу численного решения уравнений в частных производных исключительно многогранным исследованием.

Наиболее часто используются следующие виды сеток:

а) прямоугольная; б) полярная; в) треугольная; г) скошенная.

Запишем несколько формул, выражающих производные функции двух переменных в конечных разностях, для сетки с квадратной ячейкой и — шагом сетки (см. рисунок):

Получим также формулу для смешанной производной:

Можно выразить и лапсиан:

Информацию о коэффициентах при значениях функции в выражениях для конечно-разностных аналогов производных удобно представлять с помощью вычислительных шаблонов, являющихся диаграммами, показывающими, какой вклад вносят узлы сетки в рассматриваемую производную. Ниже приводятся вычислительные шаблоны для наиболее часто встречающихся производных.

Аналогично , , и т. д., например:

Напомним, что D 2f=

Все приведенные вычислительные шаблоны имеют погрешность порядка h .

Следует отметить, что можно построить и более точные (имеющие меньшую погрешность) вычислительные шаблоны, если включить в рассмотрение дополнительные узлы. В основе всех построенных до сих пор вычислительных шаблонов лежит центрально — разностная аппроксимация. Иногда, чтобы свести к минимуму распространение ошибок, пользуются левыми и правыми разностями.

Вычислительными шаблонами следует пользоваться с осторожностью, так как построенное с их помощью разностное уравнение, аппроксимирующее дифференциальное уравнение в частных производных, при счете может оказаться неустойчивым. Разностная схема считается неустойчивой, если погрешность, каково бы ни было ее происхождение, с течением времени не убывает.

Границы неправильной формы.

Нередко приходится иметь дело с областями неправильной формы. Хотя границы таких областей нельзя точно задать с помощью какой-либо одной из указанных сеток, существуют специальные методы, с помощью которых можно так модифицировать стандартные сетки, что они позволяют описать границу сложной конфигурации.

Вычислительные шаблоны для конкретного дифференциального уравнения в частных производных можно видоизменить так, чтобы учесть неправильную форму границ рассматриваемой области. Для этого, записывая производные в центрально-разностной форме, следует учесть вклад узлов, лежащих на границе области. В качестве примера рассмотрим вычислительный шаблон уравнения Лапласа в области ограниченной произвольной кривой.

Вторые частные производные для узлов, лежащих на границе области, можно записать в виде.

;

Сложив две производные, получим D f. После ряда преобразований найдем:

Соответствующий вычислительный шаблон представлен ниже.

Применив вычислительный шаблон к каждому из n узлов сетки, получим систему n уравнений, которая может быть линейной, если исходное уравнение имеет соответствующую структуру. В этом случае придется решать систему уравнений вида:

X=

Обычно матрица коэффициентов оказывается ²разреженной² (содержит много нулевых элементов), так как в большей части вычислительных схем используется лишь несколько соседних узлов, а не все узлы сетки.

Методы решения таких уравнений делятся на прямые и итерационные. Прямые методы позволяют получить точное решение, выполнив конечное число операций. Примером прямого метода может служить правило Крамера для решения совместных линейных алгебраических уравнений. Обычно для больших систем уравнений прямые методы неэффективны, так как при их применении требуется выполнение огромного объема вычислений и очень большой объем памяти ЭВМ. Поэтому чаще всего пользуются итерационными методами. Сущность итерационных методов заключается в многократном повторении одного и того же простого алгоритма, который дает результат, постоянно приближающийся к точному решению. Итерации начинаются с задания начального приближенного решения. Затем начальные значения переменных в узлах сетки последовательно меняются, пока не достигается заданная точность решения. Быстрота сходимости итерационного метода сильно зависит от степени точности начальной аппроксимации. Поэтому интуиция инженера может оказать большое внимание на эффективность вычислительного процесса. Итерационные методы подразделяются на точечные и блочные. В первом случае алгоритм используется для модификации приближенного решения в одном узле сетки, покрывающей область. Во втором случае решение модифицируется сразу в группе узлов сетки. Наиболее часто применяемые точечные методы: Метод Якоби, метод последовательных смещений, метод последовательной верхней релаксации. Эти методы знакомы по курсу ²Численные методы и оптимизация², поэтому, здесь они рассматриваться не будут.

Рассмотрим пример решения дифференциального уравнения в частных производных.

Пример 3. Определить прогибы прямоугольной шарнирно-опертой пластины при распределенной нагрузке, направленной перпендикулярно плоскости пластины.

Будем рассматривать изотропную пластину постоянной жесткости. Разрешающее уравнение такой пластины имеет вид:

где w = w (x, y) — функция прогибов, q =q (x, y) — поперечная распределенная нагрузка,

Здесь D = — цилиндрическая жесткость

Разделим пластину в каждом направлении на четыре части:

Точки 1 — 9 — внутренние узловые. Точки III — IX граничные точки.

Используем формулы (или шаблоны):

;

;

Точка 1.

+

Последние два условия, записанные в конечных разностях, дают:

; ;

Таким образом, алгебраическое уравнение, соответствующее первой узловой точке, принимает вид:

и уравнение, соответствующе 2-ой узловой точке принимает вид:

Для упрощения решения положим q=q0=const, Dx=Dy=a/4, a=b, т. е. имеем квадратную пластину при равномерном давлении и сетку с квадратной клеткой. Тогда из симметрии следует

w1=w3=w7=w9; w2=w4=w6=w9. Тогда разрешающая система алгебраических уравнений с учётом вида уравнений, построенных для узловых точек 1, 2 и 5 будет иметь вид:

— 16w2 + 2w5 = 20w1 qa4 / 256 D

-16w1 + 28w2 — 8w5 = qa4 / 256 D (5.3.22)

8w1 —32w2 + 20w5 = qa4 / 256 D

Из решения этих уравнений имеем:

Максимальный прогиб (в точке 5) :;

Точное решение:

Ознакомившись с МКР, нельзя не отметить исключительную простоту и ясность его принципов. Поэтому может показаться удивительным, что после относительно короткого периода популярности и бурного развития ныне этот метод используется все реже.

Назовем три главные причины вытеснения этого метода из практики.

1. Решение систем вида, аналогичному системе из трёх уравнений (5.3.22) рассмотренного примера выполняется очень быстро. Сложность кроется не в решении, а в составлении таких систем уравнений. В рассмотренных выше примерах мы, в целях упрощения, ограничивались прямоугольной областью. В большинстве практически важных задач область определения решения имеет более сложную форму (см рисунок).

В этом случае точки, в которых заданы граничные условия не всегда попадают на узловые точки равномерной сетки. Об этом мы говорили раньше. Кроме того, как мы убедились, при рассмотрении конкретных задач на границе могут задаваться не только значения некоторой функции, но и ее производные, или даже их комбинации. В результате помимо однотипных аккуратных уравнений типа (5.3.21) (5.3.22) в систему вклиниваются уравнения совсем другого вида. В этом случае матрица системы уже имеет не такой простой вид и имеет ряд нестандартных строк..

Таким образом, первая причина первая – сложность задания граничных условий.

2. Очень часто решение дифференциального уравнения оказывается быстро меняющимся на одних участках и гладким на других. Таково, например, решение задачи о краевом эффекте. Так в топливном баке, изображенном на рисунке, в зоне стыка цилиндрической обечайки шпангоута и сферического днища возникают изгибные деформации, которые быстро затухают по мере удаления от места стыка. Для того, чтобы численное решение на участке быстрого изменения функции было достаточно точным, шаг конечно-разностной сетки должен быть очень малым. В то же время на удалении от зоны краевого эффекта в использовании такого же мелкого шага нет никакой необходимости. Возникают два варианта решения проблемы: 1) во всей области задать малый шаг и получить систему с огромным количеством неизвестных; 2) использовать переменный шаг и значительно усложнить выражения конечно-разностных аппроксимаций производных.

Поэтому причина вторая – сложно обеспечить различную точность решения для различных участков области.

3. При расчете прочности какой-либо реальной конструкции, оказывается, что для различных ее частей необходимо использовать различные дифференциальные уравнения. Так, например, для крыла работа поясов лонжеронов хорошо описывается с помощью уравнений растяжения-сжатия стержня; для стенок лонжеронов и нервюр хорошей математической моделью являются уравнения плоской задачи теории упругости; для обшивки подходит безмоментная теория оболочек. Между тем каждая из этих теорий описывается различными дифференциальными уравнениями. Значит, конечно-разностные аппроксимации этих уравнений будут различными. Кроме того, основные неизвестные в этих системах дифференциальных уравнений могут оказаться различными по физическому смыслу. Следовательно, возникает проблема увязки решений друг с другом. Таким образом, третья причина вытеснения МКР – сложности, возникающие при объединении различных математических моделей в единую расчетную схему.

Конечно, все эти три проблемы не являются неразрешимыми. В период примерно тридцатилетнего периода активного использования разностных методов разработаны способы решения многих задач математической физики, в том числе и механики деформируемого твёрдого тела. Дело, однако, в том, что родившийся в 1956 году метод конечных элементов (МКЭ) очень просто решает большинство из перечисленных проблем

Итак, с середины 50-х годов прошлого столетия интенсивно развивающийся метод конечных элементов (МКЭ), впервые применённый для описания сплошных сред и с тех пор завоевавший известность исключительно полезного инженерного метода, стал широко применяеться в гидродинамике, аэродинамике, теории поля, при расчете сложных напряженных состояний и в других областях. Хотя метод конечных элементов применяется для решения тех же задач, что и метод конечных разностей, основаны они на разных идеях.

В методе конечных разностей производится аппроксимация производных, входящих в дифференциальные уравнения.

В методе конечных элементов аппроксимируется функция в объёме (площади, протяжении) конечного элемента.

Для этого физическая задача заменяется кусочно-гладкой моделью, отдельные части которой рассматриваются как реальные физические тела, работающие каждый по своему (или одинаковому) закону. Т. е. работа сложной системы заменяется совместной работой элементов её образующих. Это позволяет инженеру использовать свое интуитивное понимание задачи.

Метод конечных элементов значительно более сложен для понимания, чем МКР, но обладает огромными преимуществами по сравнению с МКР, главное из которых заключается в возможности построения на его основе программ широкого назначения для решения широкого круга задач математической физики. Поэтому его рассмотрению в дальнейшем будет уделено самое пристальное внимание, а настоящий раздел завершим примерными рекомендациями по решению дифференциальных уравнений в частных производных.

5.3.2. Общие рекомендации по решению дифференциальных уравнений в частных производных.

Поскольку каждому уравнению в частных производных присущи свои особенности, а граничные условия делают каждую задачу непохожей на другие, то практически невозможно сформулировать общие рекомендации, которые были бы полезны при решении таких уравнений. Однако во всех случаях полезно иметь в виду следующие правила:

1. Сначала следует выяснить, какова должна быть точность искомого решения. Если она высока, то для решения данного дифференциального уравнения может потребоваться весьма мелкая сетка или разбиение тела на очень малые элементы.

2. Затем надо внимательно изучить форму области, в которой отыскивается решение. Учесть симметрию и т. д.

3. Следует тщательно выбирать начальные значения переменных. При использовании итерационных методов скорость сходимости прямо зависит от близости исходных данных к решению.

Если хорошее исходное приближение задать не удается, то может оказаться полезным разделить решение задачи на два и более этапов. На первом этапе с помощью весьма грубой сетки или разбиения на очень крупные элементы получают хорошее исходное приближение, а затем уже ищут точное решение на гораздо более мелкой сетке или разбивая тело на мелкие элементы.

4. Следует выбрать метод, более всего подходящий для решения данной задачи.