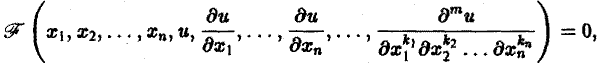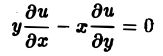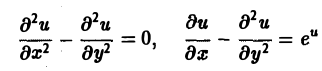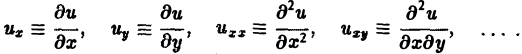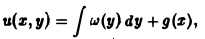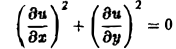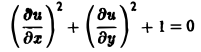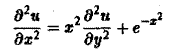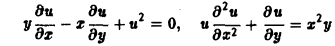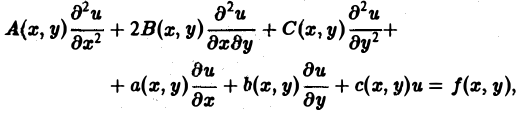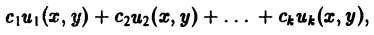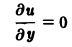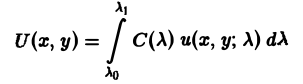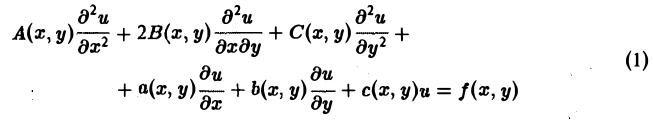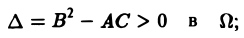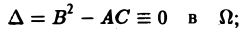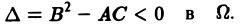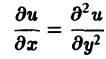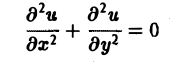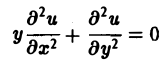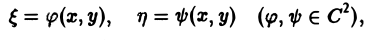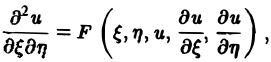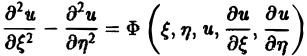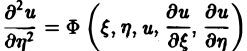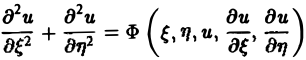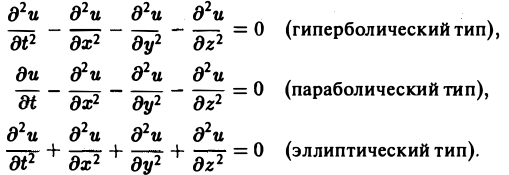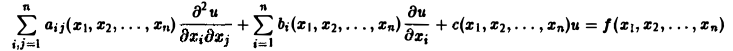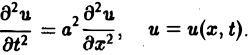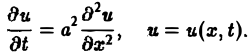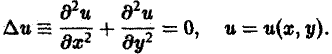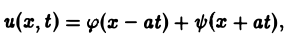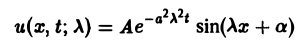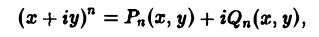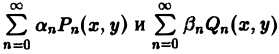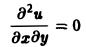Дифференциальные уравнения в частных производных в экономике

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

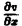
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 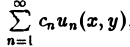, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 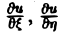и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 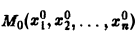и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 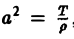где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 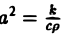где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

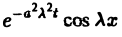
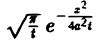
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальные уравнения в частных производных в экономике

Если неизвестная функция зависит от одной независимой переменной, то Д.у. называется обыкновенным если рассматривается функция многих переменных и в уравнении содержатся частные производные — уравнением в частных производных (с частными производными). Порядком Д.у. называется высший из порядков производных или дифференциалов, входящих в уравнение. [c.91]

Управляемый фактор 371 Управляющая информация 413 Управляющая система 371 Управляющее воздействие 371 Управляющие параметры 258, 371 Уравнение обмена 372 Уравнение отклика 251 Уравнение регрессии 305 Уравнения бюджета потребителей 152 Уравнения в частных производных [c.493]

В качестве исходного уравнения переноса и турбулентной диффузии примеси рассмотрим следующее дифференциальное уравнение в частных производных [c.92]

Комплекс моделей лесных ресурсов включает локальные, субрегиональные и региональные модели. Имеются как сосредоточенные (описываемые в терминах обыкновенных дифференциальных уравнений), так и распределенные (с уравнениями в частных производных) региональные модели. [c.174]

Левая часть равенства (9.245) зависит от вида функции п и ее частных производных, что позволяет получить уравнение в частных производных для функции п, общее решение которого и является искомым классом зависимостей. Ниже рассмотрены примеры решения обратной задачи оптимального управления для конкретных систем, показывающие, что рассмотренный класс задач достаточно широк. [c.394]

Как видно, сумма отклонений имеет положительный знак и, следовательно, теоретическая линия регрессии систематически занижает расчетные величины моделируемого признака по сравнению с фактическими. Однако расчет параметров логарифмической функции по критерию (3) с использованием обычного метода решения системы уравнений в частных производных невозможен. Продифференцируем следующую форму по «а и и [c.84]

Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]

На микроуровне фазовые переменные распределены в пространстве (распределенные модели). Модель чаще всего представляется дифференциальными уравнениями в частных производных. [c.61]

Задачи с уравнениями в частных производных [c.102]

ЗАДАЧИ С УРАВНЕНИЯМИ В ЧАСТНЫХ ПРОИЗВОДНЫХ 105 [c.105]

Метод Монте-Карло основан на статистических испытаниях и по природе своей является экстремальным, может применяться для решения полностью детерминированных задач, таких, как обращение матриц, решение дифференциальных уравнений в частных производных, отыскание экстремумов и численное интегрирование. При вычислениях методом Монте-Карло статистические результаты получаются путем повторяющихся испытаний. Вероятность того, что эти результаты отличаются от истинных не более чем на заданную величину, есть функция количества испытаний. [c.19]

Следуя обозначениям (11) из 3f, гл. III, посвященного прямым и обратным уравнениям Колмогорова и вероятностному представлению решений уравнений в частных производных, обозначим [c.413]

Многие модели управляемых систем основаны на аппарате дифференциальных уравнений как в обыкновенных, так и в частных производных. При исследовании систем с распределенными параметрами, в зависимости от вида используемых дифференциальных уравнений в частных производных, выделяют такие типы задач оптимального управления, как параболические, эллиптические или гиперболические. [c.199]

Далее, опираясь на выводы теоретической экономии, я строю дифференциальное уравнение в частных производных, которое связывает сумму капитала (К), населения (А) и размеры дохода (Е). Это уравнение таково [c.505]

Из теории дифференциальных уравнений в частных производных известно, что в этом случае система имеет единственное (локальное) решение тогда и только тогда, когда система функций спроса такова, что матрица [c.95]

В последнее время наряду с традиционным математическим аппаратом (обыкновенные дифференциальные уравнения, уравнения в частных производных, математическая статистика и т.п.) все чаще используются и другие менее традиционные средства клеточные автоматы, нейронные сети и когнитивное моделирование. Именно этот способ моделирования социально-экономических процессов и будет рассмотрен. [c.212]

В случае если число параметров мало (Сох et al., 1985), приближение модели к наблюдаемым ценам будет плохим, особенно для специфических временных структур. Кроме того, уравнение в частных производных редко допускает решение в законченном виде (такое решение можно получить лишь тогда, когда независимые переменные представлены в простом виде). Если решения в законченном виде не существует, остается единственный путь — использовать численные методы, подобные методу Монте-Карло. [c.64]

Система уравнений для определения скоростей фаз (2.19) есть система уравнений в частных производных, поскольку каждое уравнение можно рассматривать как обыкновенное дифференциальное лишь вдоль траектории движения той фазы, для которой оно записано. Чтобы рассматривать эти выражения как обыкновенные дифференциальные уравнения, нужно сделать допущения о поле скоростей сплошной фазы. Простейшее из них заключается в том, что/направления движения фаз совпадают. [c.36]

Возможность решения поставленной задачи в виде соотношений (6.22), где q, qz и q являются функциями только одной переменной z, означает, что систему дифференциальных уравнений в частных производных (6.7) — (6.9) с интегральным условием (6.10) и граничными условиями (6.11) можно свести к системе обыкновенных дифференциальных уравнений с соответствующими интегральным и граничными условиями для отыскания неизвестных функций q, q% и 0 и сколь угодно больших х, Т (x,t) -больше нуля. Это объясняется неточностью физических предпосылок, лежащих в основе теории теплопроводности, и противоречии молекулярно-кинетической теории распространения тепла в телах. Процесс распространения тепла в полубесконечном стержне при потере тепла с боковой поверхности, описывается однородным уравнением в частных производных а2 Тм-Т,-в 2Т=0 (1) [c.21]

Смирнов М.М Дифференциальные уравнения в частных производных второго лорядка .М.Наука. 1964.210с 2.Горин А.Ф К решению неоднородных уравнений математической физики Деп.ВИНИТИ.М. 1984.14с. [c.22]

Процесс распространения тепла в шкиве при торможении описывается уравнением / Е.И.Кошляков, Э.Б.Глинер, М.М.Смирнов Уравнения в частных производных математической физики. М., Высшая школа 1970/ -. [c.172]

Скорость вращательного движения газа с учетом сил трения в вихре определяется из уравнений Навье-Стокса для сплошной среды в цилиндрических координатах /И.Е.Кошляков.Э.Б Глинер.М. М.Смирнов. Уравнения в частных производных математической физики. М., Высшая школа 1970г./ [c.175]

Метод локальных вар наций и релаксационный метод. В [86 ] метод локальных вариаций был распространен на задачи минимизации функционалов от функций нескольких независимых переменных. Хорошо известно, что многие задачи математической физики (краевые задачи для уравнения Лапласа, для бигармонического уравнения и другие) могут быть сформулированы либо как задачи на минимум соответствующего функционала, либо как задачи с уравнениями в частных производных (эти уравнения — суть уравнения Эйлера для вариационной формулировки). Применительно к таким задачам метод локальных вариаций состоит из двух элементов. [c.134]

Уравнение (10 ) — что уравнение в частных производных, выведенные Блэком и Сколсом (1973) для определения стоимости любого производного финансового инструмента. Для разных типов производных финансовых инструментов уравнение имеет разные решения, которые зависят от ограничивающих условий для каждого из этих типов оцениваемых производных финансовых инструментов. Для Европейских опционов ограничивающие условия те же, что и приведенные в гл. 8, а именно [c.476]

Пример 8. Метод Уизема. Рассмотрим линейное однородное дифференциальное уравнение в частных производных [c.139]

Седьмая глава (математическое приложение) посвящено описанию нового подхода к решению задач оптимальной остановки многомерных диффузионных процессов. Этот подход основан на использовании связи между граничными задачами для диффузионных процессов и задачей Дирихле для уравнений в частных производных эллиптического типа. Решение задачи Дирихле рассматривается как функционал, зависящий от области продолжения наблюдений. Оптимизация этого функционала на множестве областей продолжения наблюдений проводится вариационными методами. Описанный подход применяется к задаче оптимальной остановки двумерного геометрического броуновского движения с функционалом, представимом в виде математического ожидания однородной функции (произвольной неотрицательной степени однородности) от указанного процесса в момент остановки. К задачам такого типа и сводится исследование задачи выбора оптимального момента инвестирования. [c.14]

Введение условий равновесия для рынков приводит к дифференциальному уравнению в частных производных (PDE — partial differential equation). Это уравнение зависит от параметров модели и рыночной цены риска. Для оценки рыночной цены риска используются различные методы. Первый метод предполагает оценку параметров модели путем построения функции, наилучшим образом приближенной к исследуемым историческим данным. После оценки параметров цена риска может быть найдена с помощью функции дисконта, выведенной из текущих цен дисконтных облигаций. В этом случае модельное приближение к историческим данным может иметь достаточную точность, но найденная цена риска часто оказывается неприемлемой. Второй путь основан на одновременной оценке параметров модели и цены риска на примере дохода от облигации с нулевым купоном в различные моменты времени. [c.64]

Аффинные системы интенсивно исследуются начиная с конца 70-х годов. Ряд результатов уже подитожен в нескольких монографиях, из которых отметим 2. В обзоре [4] имеются ссылки на ряд работ до 1985г., поэтому из ранних публикаций отметим лишь работу 5] по преобразованию аффинной системы к каноническому виду. Метод нелинейной стабилизация предложен в [6] для стабилизации программных движений аффинных систем с векторным управлением при наличии неопределенностей. Доказательство теоремы 1 в более общем случае можно найти в [7]. При синтезе управления методом нелинейной стабилизации используется решение системы уравнений в частных производных первого порядка (7.2). В тех случаях, когда [c.281]

Что такое дифференциальное уравнение и зачем оно нужно?

На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.

Дифференциальные уравнения – простейшие виды

Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?

Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.

То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.

Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=\int f(x)dx.$$

Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)\cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$\int \frac=\int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.

Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).

Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.

Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.

Пример применения дифференциального уравнения в экономике

Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.

Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.

Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.

Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.

С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.

Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = \int (10-0,2q)dq = 10 q-0,1q^2+C. $$

Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.

Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.